基于GB/T 34019标准与ASME Ⅷ-3标准的钢制瓶式容器疲劳寿命分析

袁舒梦，黄 淞，惠 虎

(华东理工大学 机械与动力工程学院，上海 200237)

0 引言

压力容器是石化行业中的一种特殊设备，由于其工作环境及盛装介质的特殊性，因而相对于其他设备，要求其具有较高的安全性[1-4]。由于高压、超高压容器有较大的壁厚、不均匀的应力分布等因素的存在，在容器的制造及使用过程中容易产生裂纹及其他缺陷，容器结构在交变载荷的作用下将导致裂纹持续扩展，最终发生疲劳破坏，这是导致压力容器发生泄漏或破坏的最直接原因[5]。据统计，压力容器运行过程中有75%以上的破坏是由于疲劳引起的[6-7]。

因此，高压容器的疲劳失效问题越来越引起重视。目前很多国家已经将压力容器的疲劳失效问题列入了规范中，如美国的ASME BPVC Section Ⅷ-3《高压容器建造另一规则》、日本的KHKS 0220《超高压气体设备标准》、英国的BS 5500《非直接火焊制压力容器规范》等。我国一直缺少针对超高压容器的建造标准，长期以来都是参考国外相关标准，GB/T 34019—2017《超高压容器》的颁布填补了我国承压设备标准体系的空白[8]。

GB/T 34019与ASME Ⅷ-3标准给出了基于断裂力学计算容器疲劳寿命的方法。对于含初始裂纹缺陷的高压、超高压容器来说，基于断裂力学方法预测疲劳寿命比传统的疲劳设计曲线法更合适，这是因为传统的疲劳设计曲线法是建立在光滑试样的基础上，考虑疲劳强度减弱系数后估算疲劳寿命，该方法偏于保守。但是，GB/T 34019和ASME Ⅷ-3在计算疲劳寿命时存在一定的差异。GB/T 34019给出了疲劳裂纹扩展分析的断裂力学方法，ASME Ⅷ-3给出了基于失效评定图的、更为复杂的疲劳寿命计算方法，基于FAD图的裂纹缺陷安全评价方法被广泛采用[9-11]。

KELTJENS[12]讨论了API 579-1/ASME FFS-1和ASME Ⅷ-3在计算应力强度因子时的差异，同时将未爆先漏分析中失效评定图的使用与ASME Ⅷ-3中的方法进行了比较，最终提出了一种简化的、基于疲劳裂纹扩展的寿命研究方法。

为确保高压容器长期安全可靠的运行，疲劳寿命分析必须采用合适的方法，从而掌握裂纹对容器疲劳寿命的影响规律，并准确预测疲劳寿命。因此，本文借助ANSYS有限元软件提取沿壁厚方向分布的环向应力，分别按照GB/T 34019标准和ASME Ⅷ-3标准编写压力容器疲劳寿命的计算程序，分析比较两种标准在进行疲劳寿命计算时的差异，重点考察应力强度因子解和疲劳失效判据的影响，本研究对于准确预测及评估含裂纹缺陷的钢制瓶式容器疲劳寿命具有重要意义。

1 基于断裂力学的疲劳寿命计算方法

采用断裂力学方法计算压力容器的疲劳寿命，要求容器存在初始裂纹。如果是校核含缺陷容器的剩余寿命，则该裂纹尺寸应为无损检测实测再规则化后的裂纹尺寸；如果是对容器进行抗疲劳设计，则需要假设容器内部存在无损检测无法检出的微小椭圆形裂纹。在初始裂纹的基础上，断裂力学方法通过以下思路计算容器的疲劳寿命：(1)针对已经存在的裂纹，计算疲劳载荷作用下该裂纹尖端的应力强度因子；(2)以裂尖的应力强度因子为裂纹扩展驱动力，计算裂纹在一定疲劳循环次数内产生的裂纹扩展量；(3)对扩展后的裂纹采用断裂韧度、裂纹尺寸等判据，评价裂纹是否失效。通过循环以上三个过程，可计算得到容器的疲劳寿命。本节首先简要介绍GB/T 34019和ASME Ⅷ-3标准中基于断裂力学计算容器疲劳寿命的方法。

1.1 应力强度因子的确定

1.1.1 GB/T 34019应力强度因子的确定

GB/T 34019附录F中，容器内壁轴向半椭圆形裂纹的应力强度因子的计算方法见图1(图中a,l,t分别为裂纹的深度、长度以及容器的壁厚)。

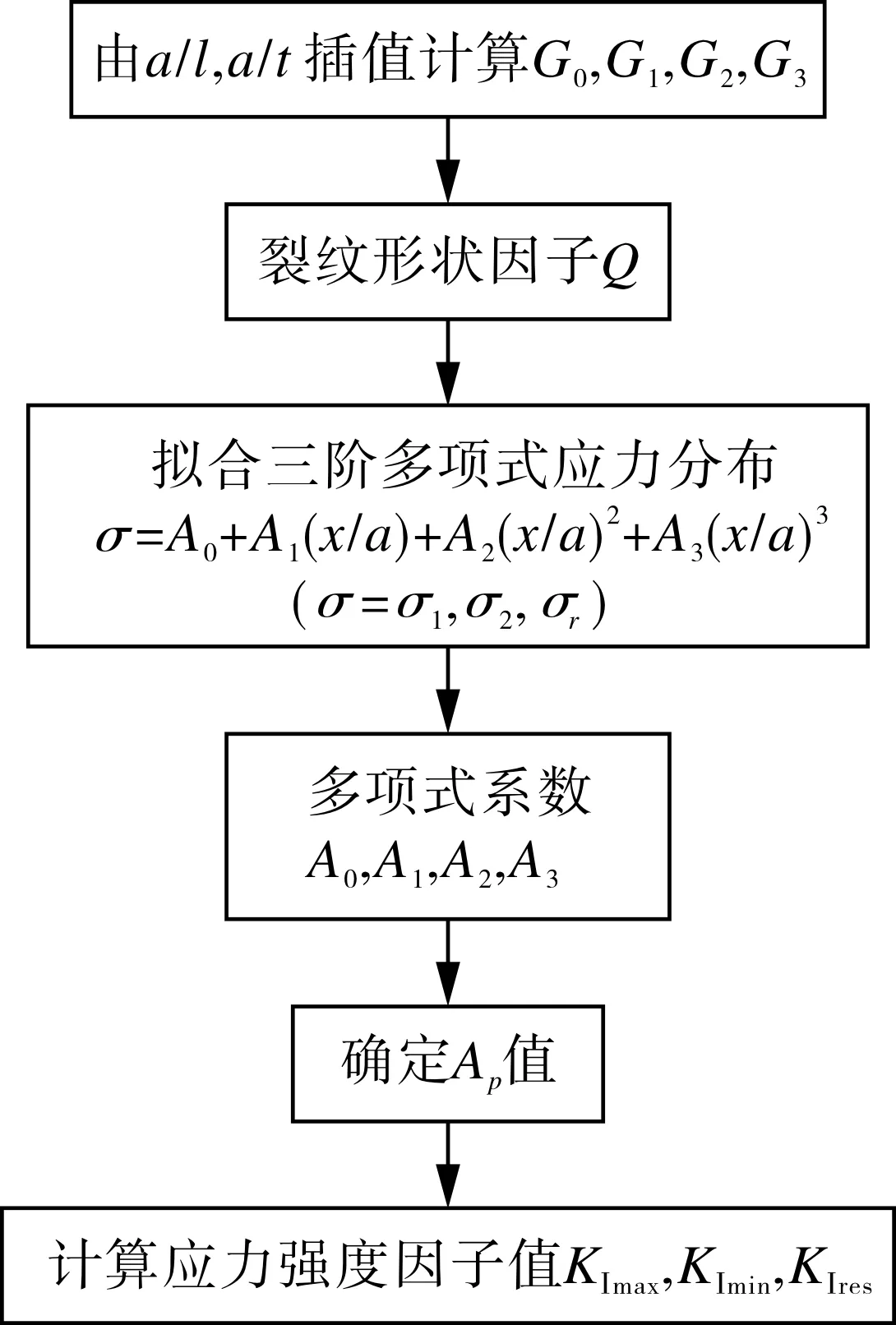
图1 GB/T 34019应力强度因子计算方法

在a/t≤0.8范围内，裂纹最深处和靠近自由表面处应力强度因子的计算公式为:

(1)

式中，Ai(i=0～3)为应力分布系数；如果压力作用在裂纹表面上,AP取容器的内压力p,MPa，对其他裂纹，AP=0；Gi(i=0～3)为表面修正系数；a为裂纹深度,mm；Q为裂纹形状系数。

Q=1+4.593(a/l)1.65-qy(0≤a/l≤0.5)

(2)

式中，qy为塑性区修正因子，当计算裂纹扩展速率时，qy=0。

1.1.2 ASME Ⅷ-3应力强度因子的确定

ASME Ⅷ-3 KD-4中在通过断裂力学评价疲劳寿命的方法时，引用了API 579-1/ASME FFS-1中的失效评定图法(FAD)，API 579-1附录9B.5.11给出了圆柱壳轴向半椭圆形表面裂纹的应力强度因子的计算方法，如图2所示(图中,x为裂尖所在位置，t为容器壁厚)。

图2 ASME Ⅷ-3应力强度因子计算方法

API 579-1 Part 9中提供了圆柱壳轴向半椭圆形表面裂纹的四阶多项式应力强度因子的计算公式，即:

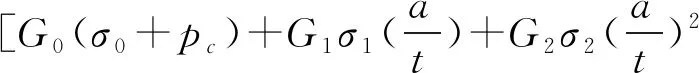
(3)

式中，G0～G4为与裂纹深度和几何形状有关的影响函数；σ0～σ4为四阶多项式应力分布系数；Q为塑性形状因子。

(4)

1.2 疲劳裂纹扩展量

GB/T 34019和ASME Ⅷ-3在计算疲劳裂纹的扩展时均采用修正的Paris公式，即:

(5)

式中，C,m为材料常数；f(RK)为应力比RK的函数。

(6)

(7)

ΔK=KⅠmax-KⅠmin

(8)

Paris公式及其各种修正形式被广泛地应用于描述疲劳裂纹扩展速率。图3示出疲劳裂纹扩展速率曲线(图中，da/dN为裂纹扩展速率，ΔK为应力强度因子幅，ΔKth为应力强度因子门槛值)。断裂力学认为，疲劳裂纹的发展过程可以被分为如图3所示的3个阶段[13]：第1阶段为疲劳裂纹的萌生阶段，该阶段裂纹扩展速率da/dN很小，疲劳裂纹基本可视为不扩展，只有当裂纹前端的应力ΔK>ΔKth时裂纹才开始扩展；第2阶段为疲劳裂纹的稳定扩展阶段，可以用Paris公式定量描述裂纹的扩展，此阶段中材料的平均应力、微观结构及环境等因素对疲劳裂纹扩展速率影响较小[14]；第3阶段为疲劳裂纹的快速扩展阶段，当ΔK达到材料的断裂韧性KⅠC时，裂纹扩展速率迅速增大直至发生疲劳脆断。

图3 疲劳裂纹扩展速率

对式(5)进行积分可以获得含裂纹的钢制瓶式容器的临界裂纹循环次数，即:

(9)

但由于应力强度因子范围ΔK无法用简单的函数关系进行表达，因而积分计算无法得到临界裂纹循环次数，只能利用数值方法近似获得钢制瓶式容器的临界裂纹循环次数，如式(10)(11)所示。

(10)

(11)

为保证数值积分的精度，应不断减少裂纹扩展增量Δa，直到前后计算的疲劳循环次数没有显著偏差。

1.3 疲劳失效判据

1.3.1 GB/T 34019疲劳失效判据

根据GB/T 34019第6.5.5节，疲劳裂纹违背以下任意判据时失效。

(1)裂纹深度a≤ 0.8t；

(2)裂纹尖端应力强度因子最大值KⅠmax≤KⅠC，其中KⅠC是容器材料的断裂韧度，当进行临氢结构的疲劳分析时，采用氢致裂纹扩展应力强度因子门槛值KⅠH作为材料的临界应力强度因子，不同压力下的KⅠC和KⅠH值如表1[15]所示。

表1 临界应力强度因子

该判据的物理含义可表述为：当疲劳裂纹穿透容器壁或裂纹发生失稳扩展时，容器发生疲劳失效。

1.3.2 ASME Ⅷ-3疲劳失效判据

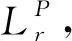
图4 FAD失效评定图

FAD轮廓线方程为:

(12)

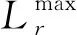
(13)

轴向半椭圆形表面裂纹的载荷比为:

(14)

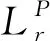
参考应力为:

(15)

式中，Pb为弯曲应力；Ms为表面修正系数；Pm为薄膜应力；g，α为与裂纹尺寸有关的系数。

断裂韧性比为：

(16)

在疲劳评定过程中，若疲劳裂纹所对应的评定点落于FAD图轮廓线之外，或其裂纹深度超过0.8t，则容器发生疲劳失效。该方法除了考虑到裂纹失稳扩展失效、裂纹穿透失效之外，还考虑了裂纹剩余韧带塑性垮塌失效的影响。

2 瓶式高压容器的疲劳寿命分析

2.1 研究对象及有限元模型的建立

为了准确预测高压容器的疲劳寿命，基于GB/T 34019标准与ASME Ⅷ-3标准中关于疲劳寿命计算的规定，利用MATLAB软件分别编写程序用于抗疲劳设计，以对比两种标准在进行疲劳寿命计算时的差异。

国内外常用的钢制瓶式容器的外直径为406,559,720 mm[16]。本文选取材料为4130X，直径为406,559,720 mm，设计压力为40，50，60，70，80，90 MPa的钢制瓶式容器为研究对象，分析氢气环境中不同设计压力、不同规格的钢制瓶式容器的疲劳裂纹扩展行为。

容器的设计壁厚采用JB 4732—1995《钢制压力容器——分析设计标准》中的壁厚公式计算得到，腐蚀余量为0 mm，计算不同设计压力、不同直径下钢制瓶式容器的壁厚，结果如表2所示。

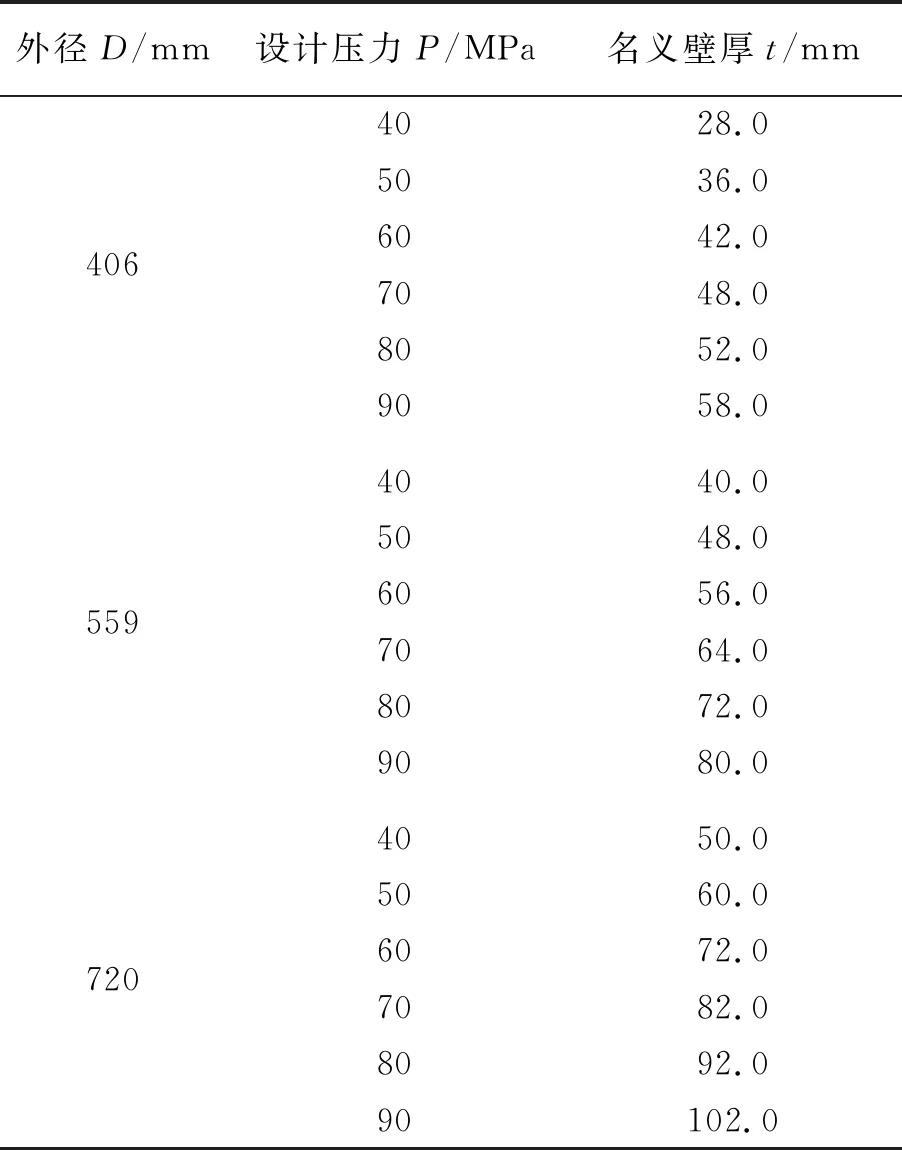
表2 钢制瓶式容器的壁厚计算

在第1.1节中介绍的应力强度因子计算方法中，均需要沿容器壁厚方向的原场弹性应力作为裂纹扩展驱动力，本文采用ANSYS软件建立瓶式容器的有限元模型，计算疲劳载荷作用下容器的环向应力，并将其作为计算应力强度因子的依据。考虑到钢制瓶式容器的结构及所受载荷均具有对称性，因此仅考虑1/8模型。单元选择Solid 186单元，模型采用六面体网格划分，壁厚方向上划分8层网格，在该模型中，单元总数60 056，节点总数69 909，网格模型如图5所示。

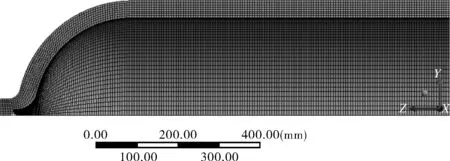
图5 网格划分

文中钢制瓶式容器的边界条件为：在容器的内表面上施加均布的内压载荷，在1/8模型的两侧和底部施加对称边界条件，加载过程如图6所示。

图6 钢制瓶式容器加载过程

2.2 有限元计算结果

对于径厚比相同的钢制瓶式容器，其应力分布规律及应力强度因子增长趋势大致相同，因此疲劳裂纹扩展规律也大致相同，故仅以直径为559 mm的Ⅰ型瓶为例进行说明。图7示出直径559 mm的Ⅰ型瓶在设计压力从40 MPa变化到90 MPa时，环向应力值随钢制瓶式容器壁厚的变化情况，图中x为裂尖所在位置，t为容器壁厚。随着容器壁厚的增加，沿壁厚方向的环向应力逐渐降低，内壁面最大，外壁面最小；且环向应力随着设计压力的增大而减小，环向应力的降低速率随设计压力的增大而增大。

图7 钢制瓶式容器沿壁厚方向环向应力的分布

2.3 疲劳分析所需材料参数

本文中疲劳分析采用的4130X材料的处理状态为调质，对于4130X高压储氢容器而言，其FAD评定需要材料强度的相关参数，具体如表3所示。计算裂纹扩展需要高压氢环境中的Paris公式参数，本文参考了文献中的数据，如表4[17]所示。表中数据是4130X钢分别在45,70,90 MPa的高压高纯氢气环境中基于原位测试方法获得的疲劳裂纹扩展参数。出于安全的角度考虑，在进行疲劳寿命分析时，数据向下兼容，分别采用45,70,90 MPa氢气环境中的Paris公式参数用于40,50～70,80～90 MPa氢气环境中的疲劳裂纹扩展计算。

表3 4130X钢的力学性能参数

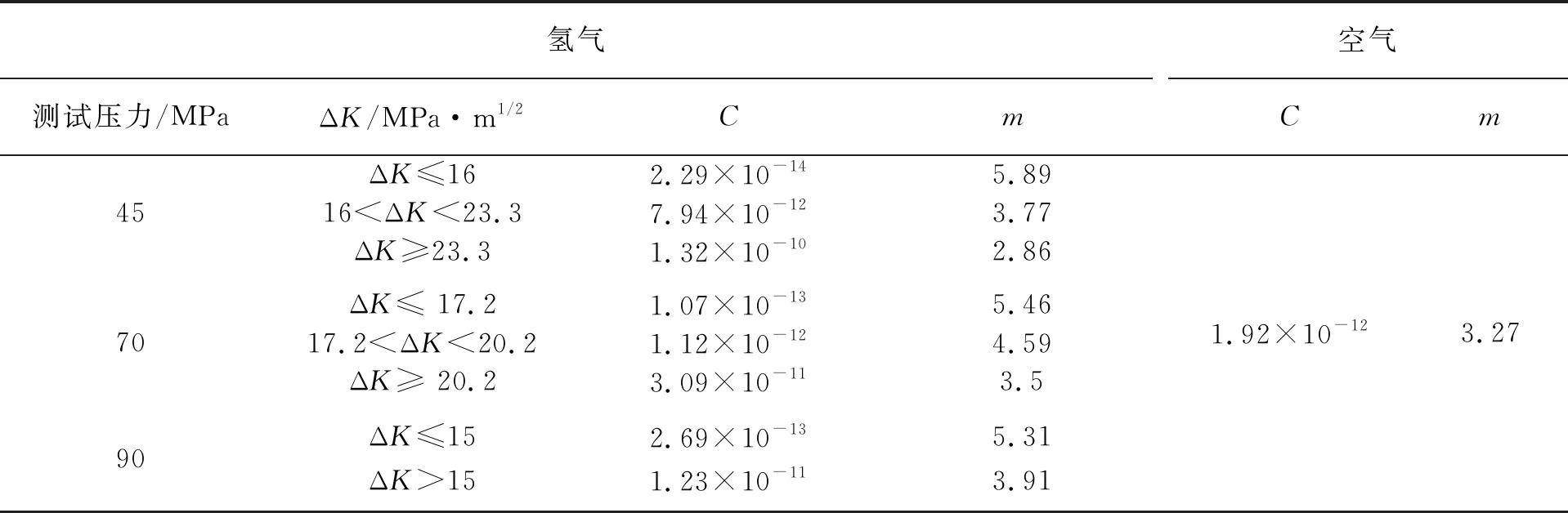
表4 4130X钢的疲劳裂纹扩展参数

3 结果分析

3.1 应力强度因子解

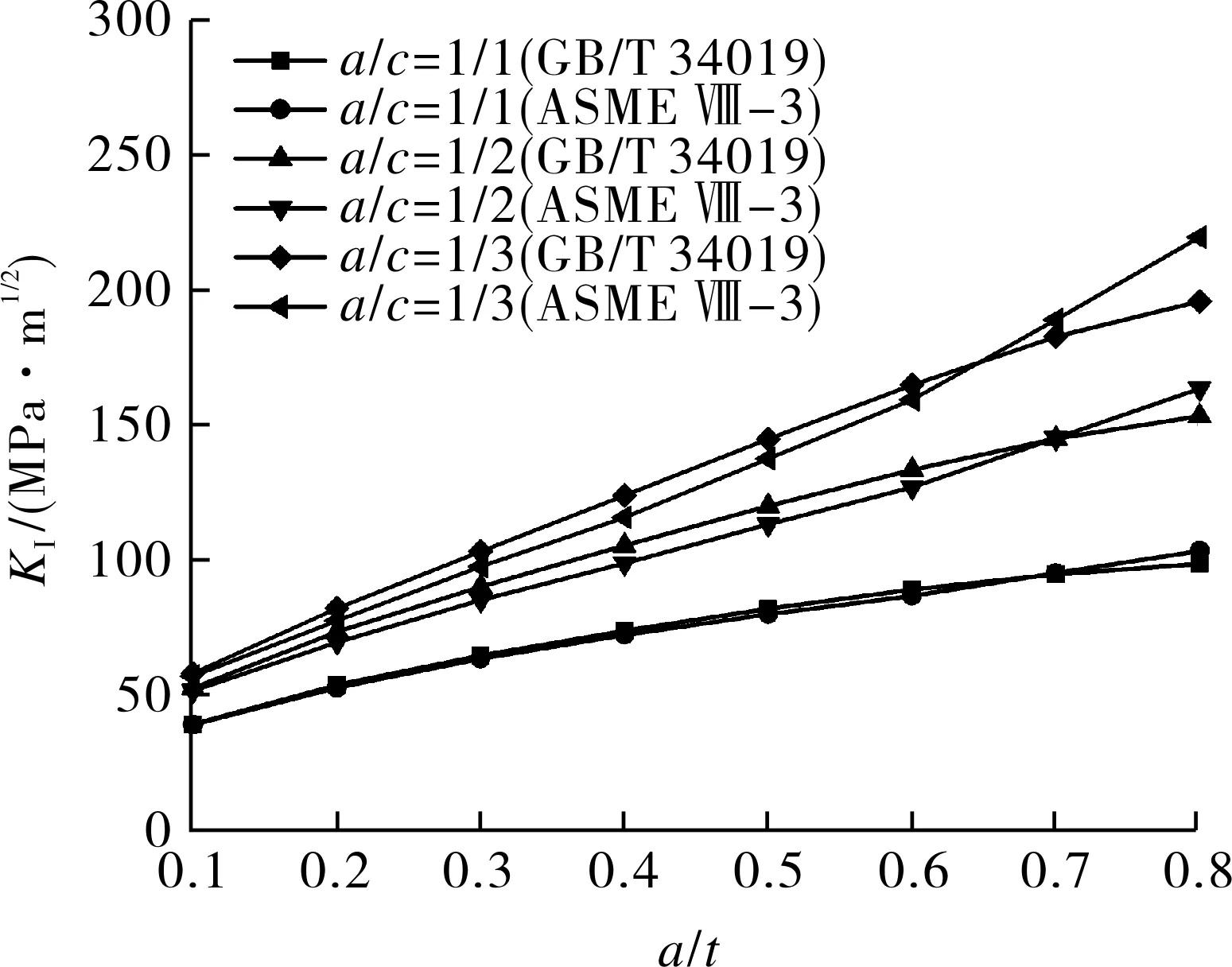
钢制瓶式容器内表面轴向半椭圆形裂纹最深处及表面处的应力强度因子的比较如图8所示。初始裂纹深度a0为0.5 mm，裂纹深长比a/c分别为1/1,1/2,1/3，由图8(a)可以看出，随着裂纹深度的增加，裂纹最深处的应力强度因子在不断增大。对于直径为406，559，720 mm，设计压力在40～90 MPa内的钢制瓶式容器，假设容器内表面存在深长比a/c=1/1，1/2，1/3的轴向裂纹时，裂纹的a/t不同，GB/T 34019标准与ASME Ⅷ-3标准的应力强度因子计算结果不同。当裂纹较浅，即a/t<0.6～0.7时，ASME Ⅷ-3的计算结果更小；当裂纹较深，即a/t>0.6～0.7时，ASME Ⅷ-3的计算结果逐渐超过GB/T 34019。裂纹表面处的应力强度因子如图8(b)所示，可见，GB/T 34019和 ASME Ⅷ-3两种标准之间的计算结果差异较小。

(a)裂纹最深处的应力强度因子

GB/T 34019与ASME Ⅷ-3之间应力强度因子计算结果的差异如图9所示。应力强度因子的计算差异与径厚比无关，而与裂纹的形状及容器的设计压力有关。

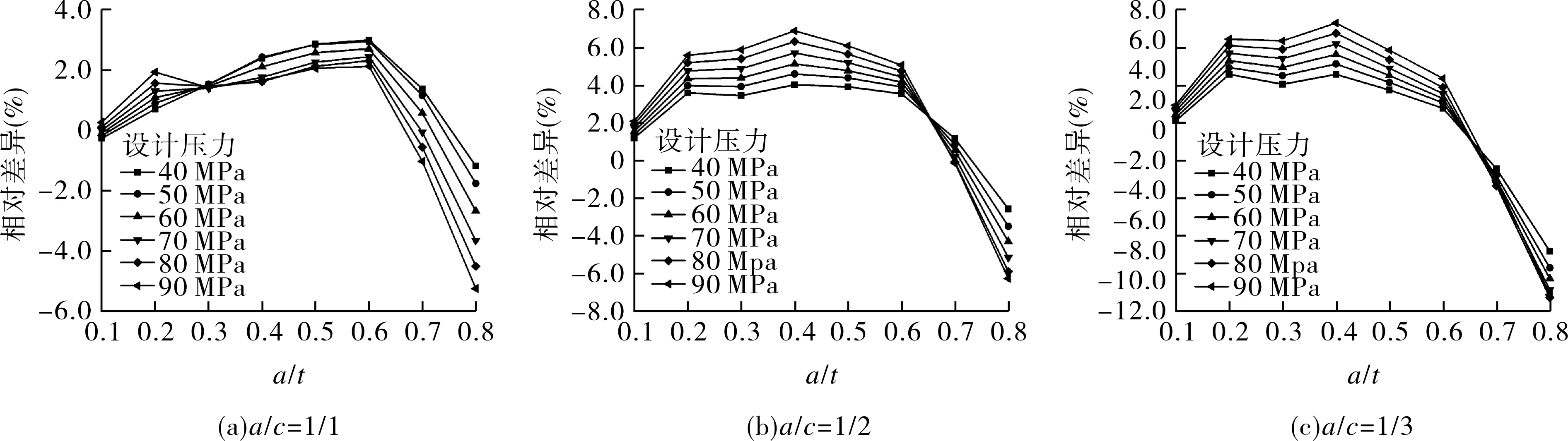
图9 GB/T 34019与ASME Ⅷ-3应力强度因子相对差异

对于半圆形裂纹(a/c=1/1)，裂纹最深处应力强度因子之间的差异最大约为5%。裂纹越扁长，即a/c越小，两个标准之间的差异越大。当裂纹的深长比a/c为1/3时，该差异可以达到11%。

容器的设计压力越高，GB/T 34019与ASME Ⅷ-3计算结果差异越大。对于单一的浅裂纹来说，设计压力越高，使用GB/T 34019标准进行评价时，应力强度因子的计算结果更大；而对于单一的深裂纹来说，设计压力越高，使用ASME Ⅷ-3标准进行评价时，应力强度因子的计算结果更大。

3.2 疲劳失效判据

疲劳裂纹扩展寿命是一个应力强度因子累加的过程，由于GB/T 34019与ASME Ⅷ-3两个标准退出疲劳循环的条件不同，因此仅对比两标准中应力强度因子计算值的大小并不能判断出临界裂纹循环次数的大小。对此，本文接下来进行了疲劳裂纹扩展的分析。假设存在沿钢制瓶式容器内表面的轴向-径向半椭圆形初始裂纹，初始裂纹深度a0为0.5 mm，初始裂纹深长比a/c分别为1/1,1/2和1/3，疲劳循环过程中裂纹自由扩展，GB/T 34019与ASME Ⅷ-3临界裂纹循环次数的对比如图10所示。

图10 GB/T 34019与ASME Ⅷ-3临界裂纹循环次数对比

对于某一固定直径的钢制瓶式容器，当设计压力增大时，临界裂纹循环次数减小。当初始裂纹的深长比a/c分别为1/1,1/2,1/3时，根据ASME Ⅷ-3标准算出的临界裂纹循环次数始终比GB/T 34019小，且a/c越大，即初始裂纹越接近于半圆形裂纹(a/c=1/1)时，两个标准计算得到的临界裂纹循环次数差异越大，相对差异最大约为15.3%。初始裂纹的形状越扁长，两个标准的相对差异越小;当初始裂纹深长比a/c=1/3时，两个标准的计算差异相对较小，约为9.4%。

图11示出直径559 mm，设计压力90 MPa的钢制瓶式容器的FAD曲线，初始裂纹深长比a/c=1/1。

(a)裂纹表面处

将GB/T 34019与ASME Ⅷ-3的失效评定点绘制在同一个坐标系内，可以看出，在本案例研究范围内，对单一浅裂纹来说(a/t<0.6～0.7)，在裂纹扩展过程中，两个标准应力强度因子计算值差别不大，但GB/T 34019仅考虑裂纹的断裂判据，忽略了裂纹剩余韧带塑性垮塌失效的影响，比ASME Ⅷ-3的疲劳判据更为宽松，因此，GB/T 34019比ASME Ⅷ-3更晚退出疲劳循环，其临界裂纹循环次数计算值也高于ASME Ⅷ-3。

随后，令裂纹继续扩展，研究裂纹从初始状态扩展至完全穿透壁厚，变成穿透型裂纹这一过程，即此时裂纹的深度a达到壁厚t的0.8倍。GB/T 34019与ASME Ⅷ-3临界裂纹扩展寿命的对比如图12所示。可见，曲线的走势与图10完全相同，即随着设计压力的升高，临界裂纹循环次数逐渐减小，且GB/T 34019标准计算得到的临界裂纹循环次数始终比ASME Ⅷ-3高，这与上文中得到的结论是一致的。

图12 裂纹穿透所需的临界裂纹循环次数

然后将该过程与上文中的裂纹从初始状态扩展至不再能满足第1.3节中的疲劳判据这一过程所得到的裂纹最终尺寸以及临界循环次数的数据绘制在同一坐标系内，如图13所示。可以看出，对于临界循环次数来说，两个过程并没有很大的差异，而裂纹的深度和长度却迅速增长，这说明尽管放宽了终止疲劳循环计算的要求，但此时裂纹也已经到达了失稳状态，即仅需要较少的疲劳循环次数，裂纹就会在短时间内沿其深度及长度迅速扩展，导致容器失效。

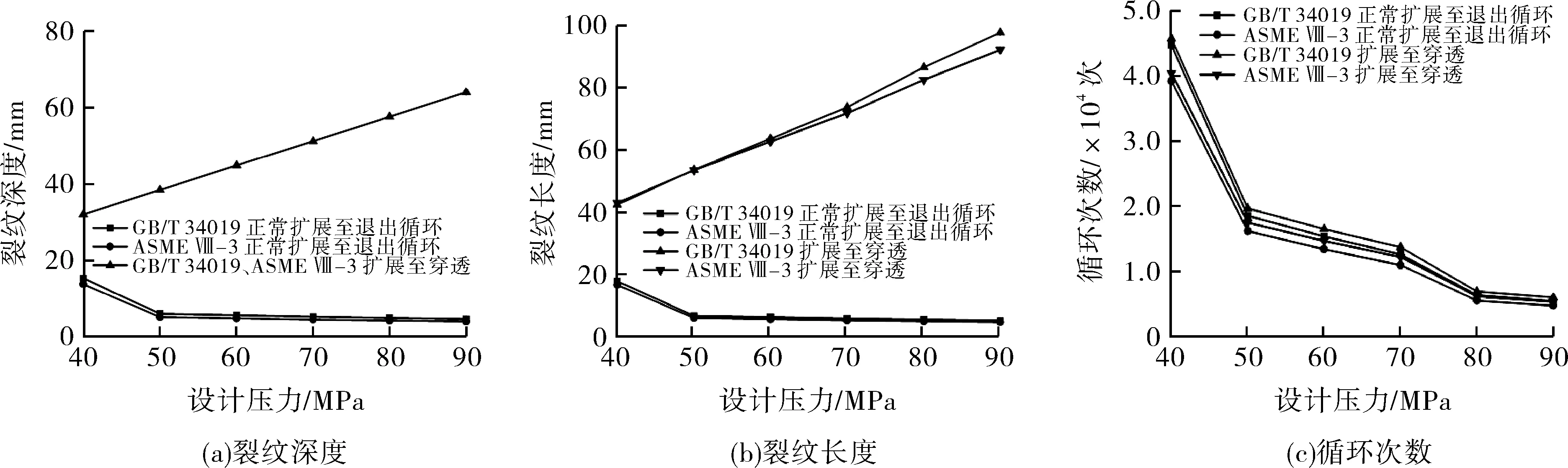
图13 裂纹正常扩展至退出循环与裂纹扩展至穿透两过程的对比(a/c=1/1)

综合上述分析可以看出，对于单一浅裂纹来说，尽管GB/T 34019的应力强度因子计算值比ASME Ⅷ-3大，但由于GB/T 34019比ASME Ⅷ-3的疲劳判据更宽松，即GB/T 34019比ASME Ⅷ-3更晚退出疲劳循环，则其临界裂纹扩展寿命更高。因此认为对于设计压力为40～90 MPa的瓶式高压容器，ASME Ⅷ-3的疲劳裂纹扩展分析方法相对更保守。

4 结论

(1)应力强度因子计算方法不同以及疲劳失效的判据不同是导致GB/T 34019与ASME Ⅷ-3疲劳寿命计算值存在差异的主要原因。

(2)对于本文研究的钢制瓶式容器内表面轴向裂纹来说，裂纹深长比a/c的变化对裂纹最深处的应力强度因子计算结果影响较大，而对裂纹表面处的应力强度因子计算结果影响较小。当裂纹较浅，即a/t<0.6～0.7时，GB/T 34019的应力强度因子值更大；当裂纹较深，即a/t>0.6～0.7时，ASME Ⅷ-3的应力强度因子值更大。

(3)GB/T 34019与ASME Ⅷ-3应力强度因子的计算差异与裂纹的形状及钢制瓶式容器的设计压力有关。裂纹的深长比a/c越小，设计压力越大，两个标准之间的差异越大，最大差异可达到11%。

(4)在本文研究范围内，钢制瓶式容器的临界裂纹扩展寿命随设计压力的增大而减小，且根据ASME Ⅷ-3标准算出的临界裂纹扩展寿命始终比GB/T 34019小，初始裂纹越接近于半圆形裂纹时，两个标准之间的差异越大，相对差异最大约为15.3%。

(5)本文研究结果表明，对于单一浅裂纹，尽管GB/T 34019的应力强度因子计算值比ASME Ⅷ-3大，但由于GB/T 34019比ASME Ⅷ-3的疲劳判据更宽松，其临界裂纹扩展寿命也更高，因此认为对于设计压力为40～90 MPa的瓶式高压容器，ASME Ⅷ-3的疲劳裂纹扩展分析方法更为保守。