分段式环形耐压壳设计与分析

狄陈阳，唐文献，张 建,，王 芳，王纬波

(1.江苏科技大学 机械工程学院，江苏镇江 212003；2.上海海洋大学 上海海洋可再生能源工程技术研究中心，上海 201306；3.中国船舶科学研究中心 深海载人装备国家重点实验室，江苏无锡 214082)

0 引言

深海空间站是一种不受海面恶劣风浪环形影响，可长期、全天候在深海进行资源开发、工程作业、军事演习的新型载人潜水器。与传统载人潜水器相比，深海空间站具有更长的水下作业时间、更大的内部容积，这对耐压壳综合性能提出了更高的要求。环形耐压壳具有稳定性好、三维空间内移动方便、人员通过性好等优点[1-2]，符合深海空间站耐压壳性能需求，可作为深海空间站的主要载人舱体。

环壳因具有柱壳、球壳无法取代的特殊优点，学者们对环壳屈曲特性展开了广泛的研究。ZHANG 等[3]采用数值分析法和试验法,研究了旋转角度对环壳屈曲载荷的影响规律。段志祥等[4-5]揭示了内压下弯管几何参数对壳体极限载荷的影响规律，并提出局部减薄后弯管极限内压计算公式。滕步刚等[6]研究了环壳内侧壳体数对环壳液压胀形过程的影响。

此外，环壳结构优化的问题也得到广泛研究。DU等[7]提出了一种带有加强肋的环形耐压壳，并用数值分析方法研究该加强结构的非线性屈曲特性。GALLETLY等[8]提出椭圆截面的形状参数会影响环壳的屈曲载荷，并采用数值分析方法得出影响规律。但环形耐压壳制造难度高，至今未有环壳成功应用于水下的案例。WANG[9]采用多边形截面代替圆截面后，发现柱壳承载能力随着截面边数的增加而增加。本文将这种以直代曲的思想应用于环壳，提出分段式环形耐压壳。由于分段环壳破坏了环壳高度轴对称回转结构，分段环壳承载能力始终低于环形耐压壳。

为此，本文基于分段环壳，尝试对其进行加强结构设计，参照中国船级社《潜水系统与潜水器入级规范》中耐压壳体极限承载力有限元分析方法进行仿真计算，采用数值分析的方法，分析椭圆截面和环肋加强后壳体的屈曲特性，考察椭圆参数、环肋厚度对壳体承载能力的影响。

1 椭圆截面分段环壳设计与分析

1.1 椭圆截面分段环壳设计

本文研究的椭圆截面分段环形耐压壳由8段柱壳依次相连构成(见图1(a))。8段柱壳的截面均为椭圆，椭圆截面长半轴为a，短半轴为b。分段环壳椭圆截面长短轴的交点相连构成轴线，且椭圆截面环壳轴线为正八边形，轴线边长为L。如图1(b)所示，当椭圆截面长半轴a与短半轴b的比值K=1时，截面为圆。截面圆的圆心构成环形耐压壳圆形轴线，环壳轴线半径为R，截面半径为r。

(a)分段环壳几何结构参数

为探究椭圆截面结构对分段式环形耐压壳屈曲特性的影响，根据等体积原则，建立等体积的环形耐压壳与椭圆截面环壳对比，模型几何参数如下：环形耐压壳轴线半径R=4 585 mm，截面圆半径r=2 467.5 mm，厚度t=140 mm。与之体积相等的分段环壳具有相同的厚度t，椭柱壳的轴线边长L=3 601.1 mm，a，b值由以下公式计算求解。

环形耐压壳体积公式：

V1=2π2r2R

(1)

椭圆截面分段环壳体积公式：

V2=8πabl

(2)

不同K值下，椭圆截面长半轴a和短半轴b数值见表1。

表1 椭圆截面几何尺寸

数值模型的求解采用三点约束方法，该方法可避免刚体运动，且不会产生额外的反作用力。该边界条件为中国船级社推荐使用的约束条件，且三点约束方法成功用于评价蛋形、桂圆形、环形旋转壳在外压作用下的极限强度[10-12]。马氏体镍钢屈强比接近1，较一般钢材屈强比高，约是普通钢材1.5倍，材料本身强度高、韧性高、热处理不变形[13]，具有一定的特殊性。且考虑到强化模型仅会使屈曲载荷接近或略低于理想弹塑性本构模型[14]，所以文中采用理想弹塑性本构模型进行仿真计算。数值计算材料参数见表2[15]，网格划分采用四边形壳单元。

表2 马氏体镍钢C250材料参数

计算方法采用基于屈曲模态的几何初始缺陷分析方法，引入0.1t的模态缺陷进行非线性屈曲分析。通过Abaqus软件进行数值计算，临界失稳压力是由“LPF-Arclength”曲线中最大载荷比例因子乘施加在壳体表面的参考载荷得到，不同K值下环形耐压壳的屈曲载荷的拟合曲线见图2。

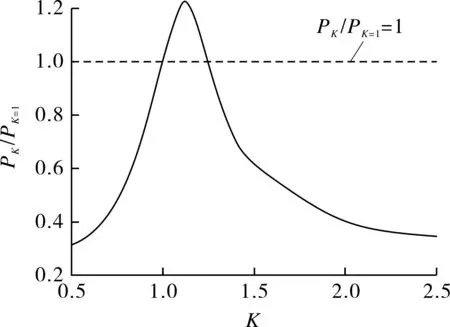
图2 椭圆截面分段环壳屈曲载荷拟合曲线

1.2 椭圆截面参数优选

由图2可以看出，当K值在0.5～2.5内变化时，分段环壳屈曲载荷随着K值的增加，呈现先上升、后下降的趋势。结合表3可知，当椭圆截面K约为1.113时，分段环壳屈曲载荷达到最大值32.249 MPa，与环壳a/b=1.17达到最高屈曲载荷结果吻合[7]。此时分段环壳能达到等体积、等壁厚的环壳1.097倍的承载能力，较未采用椭圆截面的分段环壳承载能力提高22.4%。该结果表明，基于现有成熟的大型柱壳制造技术，采用椭圆截面加强结构的分段环壳是合理的，可为环形耐压壳的制造提供一种创新思路。

表3 壳体承载能力

1.3 椭圆截面分段环壳屈曲分析

图3示出K=1和K=1.113时分段环壳以及环形耐压壳的平衡曲线，横坐标Umax/t表示失稳处的最大位移和壳体厚度的比值。

(a)分段环壳K=1

由载荷位移曲线可知，3种壳体的载荷均是随着位移的增加而表现为非线性增加，到达极大值后缓慢下降。图3还给出了模型的后屈曲模态和最大屈曲载荷下的应力分布图。

椭圆截面结构加强后的分段环壳，后屈曲模态与环壳和分段环壳相似，均表现为内环面失稳。3种壳体屈曲的最大位移点处的最大应力均大于屈服强度，表明壳体均发生了弹塑性屈曲。

2 环形加强肋设计与分析

2.1 环肋加强结构设计

为进一步提高壳体的承载能力，使用环形加强肋进行加强，如图4所示。环形加强肋位于柱壳交接处，柱壳截面长短轴之比K取1.113，环肋与柱壳斜截面的尺寸相等。此外，环肋的宽度为w，厚度T=400 mm。通过改变环肋宽度，可以考察环肋宽度对分段环壳承载能力的影响。

图4 加肋分段环壳及环肋结构

2.2 数值结果分析

在非线性数值计算过程中，壳体参数、边界条件、模态缺陷与第1.1节一致，累计考虑14种宽度。图5示出了环形加强肋对壳体承载能力影响规律曲线，以及不同环肋宽度下壳体失稳模式。

由图5和表4可以看出，分段环形耐压壳的环形加强肋厚度一定时，壳体的临界屈曲载荷随着环肋宽度的增大而增大，然后趋于平缓。即环肋的宽度达到一定阈值(400 mm)时，临界屈曲载荷值趋于稳定，到达40.850 MPa，较未加肋前承载能力提升26.7%。当环肋宽度达到400 mm这一阈值后，分段环壳的屈曲破坏均表现为柱壳的失稳，这与ZHU等[16]的柱壳水压试验结果一致，且该规律符合变形协调规律[17]。

图5 环肋厚度对分段环壳屈曲载荷的影响曲线及壳体失稳模式

表4 加肋分段环形耐压壳性能

2.3 壳体浮力系数与性能比

浮力系数是评价壳体浮力储备的重要参数，计算公式如下：

(3)

式中，ε为浮力系数；V为材料体积，即壳体本身结构体积,m3；ρ为材料密度(见表2),kg/m3；V0为排水体积,m3；ρ0为海水密度，取ρ0=1 020 kg/m3。

加肋分段环壳材料体积V、排水体积V0对应计算公式如下:

(4)

(5)

为了评价壳体抗压性能，引入性能比公式：

(6)

式中，η为性能比系数；P为屈曲载荷；W为耐压壳质量。

代入数值，并将式(4)(5)代入式(3)(6)，可计算出壳体浮力系数以及性能比，计算结果见表4，可以看出，浮力系数随着环肋厚度的增加而增加，浮力系数在0.866～1.187范围内变化，壳体浮力储备良好。当h=200 mm时，壳体具有最高的性能比40.980，且该性能比大于不锈钢制造的蛋形、桂圆形耐压壳[3]。综上所述，加肋分段环壳的环肋宽度为200 mm时具有最好的综合性能。壳体工作深度计算公式如下：

(7)

式中，h为工作水深；P为海水压强；K为安全系数，取K=1.5；g为重力加速度，取g=9.8 N/kg。

不同尺寸下加肋分段环壳临界屈曲载荷见表4。加肋分段环壳的环肋宽度为200 mm时具有最好的综合性能，此尺寸下壳体屈曲载荷为39.489 MPa，代入式(7)计算得分段环壳工作水深为2 633 m。

3 结论

(1)分段环壳数值计算表明，对于分段式环形耐压壳，当椭圆截面形状从扁平形变成竖长形时，承载能力先上升、后下降，且在椭圆长半轴与短半轴的比值K=1.113时达到最大值。

(2)优选椭圆截面参数下，分段环壳加肋尺寸计算结果表明，在环肋厚度达到临界值后，壳体承载能力趋于稳定，壳体屈曲破坏表现为柱壳失稳模式，该规律与变形协调规律一致。

(3)椭圆截面、环肋结构加强后的分段环壳，承载能力分别提升22.4%和26.7%，能够克服分段环壳极限载荷低于环壳这一局限，且设计后的壳体具有良好的浮力储备，以及优良的抗压性能。