基于三方相互体谅讨价还价的IPD团队风险分担

臧雅萱，周 直

（重庆交通大学 经济与管理学院，重庆 400074，E-mail：1298678217@qq.com）

在加快建设交通强国，推动交通运输领域新型基础设施建设的大背景下，BIM技术的推广、5G技术的应用让公路工程建设迈上了新的台阶。同时，传统交付模式下各参与方相互独立、缺乏沟通导致建设效率低下，施工方被迫承担过多风险的问题日益严重。集成项目交付模式（Integrated Project Delivery，IPD）比传统交付模式更高效[1]，是未来建设领域的新方向，是解决上述问题的有效方法。在IPD模式下要使各方真正形成持续良好的合作关系，必须公平合理地分配风险，保障各方利益。合理的风险分担方案将约束业主方利用自身优势过度转移风险使其他参与方被迫承担的行为，也可避免其他参与方为了追求眼前自身利益而损害项目整体利益，切实增加项目成功几率。国内公路工程建设项目在风险分担方案制定时，仅指出风险由一方承担或多方共同承担，并未明确各方承担的比例，容易造成合同争议及纠纷，增加合同风险。当风险发生时，各方的推卸和逃避更会让风险损失加大。因此，有必要研究IPD模式下风险分担问题。

目前，国内外对IPD模式下参与方风险分担的研究有一定成果。Govan等[2]提出将更多的风险因素分配给风险偏好方和风险承受能力强的一方。Nasirzadeh等[3]基于系统动力学的合作博弈模型定量分析了风险分配问题。Karakas等[4]开发了一个多主体系统来模拟不同情况下各方如何分担风险和相关成本。王首绪等[5]运用FAHP-熵权法对比了IPD模式与DDB模式下的参与方风险分配比例，证明了IPD模式下分配比例更合理。李寒哲等[6]从组织模式、合同两个角度对基于IPD模式的PPP项目进行风险分配研究，同时运用社会网络分析法（SNA）对IPD模式应用于PPP项目的效果进行了分析。刘增粮等[7]构建“四阶段”风险动态分担框架，针对共担风险，运用 ISM-随机合作博弈得到联合体成员的最优风险分担比例。唐碧秋等[8]利用双方讨价还价博弈探讨了BIM参与双方的风险分配问题。李宸宸[9]以商业综合体项目为背景，基于博弈论对风险进行多次分担。张瑞等[10]构建了政府部门、项目公司中专业公司和纯投资者三方相互威慑讨价还价模型，使得项目风险在“私人部门”内部间也可以得到合理分配。牛建刚等[11]运用粗糙集理论和解释结构模型得出风险分担评价指标体系。王茹等[12]提出激励池概念，量化各参与方以何种比例来分配激励池中的共享收益。

以上研究中方法各异，博弈论思想被大量运用。在讨价还价博弈的应用方面，大都简化为双方博弈。三方的博弈都以相互威慑为前提，其实质仍是双方博弈的延续。IPD模式以合作为前提，力求关系融洽，实现总体利益最大化，这种合作关系更符合相互体谅的原则。本文针对三方共同承担的风险，将以适应性预期为基础的三方相互体谅讨价还价模型[13]引入IPD模式下公路工程建设的风险分担问题，能够在尊重各方意愿的前提下，真正实现三方公平博弈。并创新性地将全过程咨询方作为IPD团队中的一方，为IPD团队的建设提供新的思路。

1 风险分配

IPD模式遵循风险共担的原则，但不一定所有的风险都分配到每个参与方。实际情况是，一部分风险由单方承担比多方共担更有利于项目进行。如项目审批、土地获取等风险应由业主一方承担，而施工技术风险则应由施工方承担。在项目建设过程中设置风险激励池鼓励和引导参与方主动承担风险并获得相应收益，也是风险共担的一种表现形式。将风险分为一方承担、两方承担和三方承担3种，分别用不同方法进行分配，能够使整体分配更合理。对此，已有许多学者进行了探索。如李宸宸[9]、赵敏华等[14]基于三方完全信息静态博弈模型识别出一方承担、双方承担和三方承担的风险因素，从而对风险进行初步分担。对于双方承担的风险，唐碧秋等[8]基于轮流出价的讨价还价理论，对完全信息和不完全信息两种动态博弈情况进行分析，使双方达成均衡，各自承担部分风险。而对于三方承担的风险，方法不一，主要有FAHP-熵权法[5]、三方相互威慑讨价还价博弈[10]、修正Shapley值法[15]等。某一风险因素具体由几方承担及两方承担时如何分配的问题，可参考上文提到的方法进行分担，风险分担路线如图1所示。经过对相关文献[9，14，16]的整理与总结得出，IPD模式下需三方共同承担的风险主要有：经济风险、信任风险、沟通风险、团队管理风险、合同风险等。本文主要应用三方相互体谅讨价还价模型对三方共同承担的风险再次分配。

图1 风险分担路线

2 基于三方相互体谅讨价还价博弈的风险分担模型

2.1 博弈三方的选择

IPD模式下公路工程建设项目的主要参与方有：业主方、设计方、监理方、咨询方、施工方等。近年来，全过程咨询的兴起为IPD模式的实施提供了新的便利。自2017年以来，国家相继发布指导意见，鼓励投资咨询、勘察、设计、监理、招标代理、造价等企业联合发展全过程工程咨询。不难看出，全过程工程咨询是未来行业发展的必然趋势，是传统设计方、监理方、咨询方等各方的有机融合，故将全过程咨询方作为IPD模式下公路工程建设项目的参与方是合理的选择。业主通过公开招标或委 托等形式选择合适的全过程咨询方及施工方，签订IPD合作协议。全过程咨询方与施工方在项目前期就参与其中，三方精诚合作，风险共担，利益共享，实现项目利益最大化。

2.2 模型假设

针对IPD模式下三方共担风险及博弈论相关理论，本文对拟构建的IPD模式下公路工程建设项目风险分担模型做出如下假设：

（1）需各方共同承担的风险在分配过程中能够被完全分担。

（2）项目建设中的各种风险因素之间相互独立，互不影响。

（3）项目所有参与方都符合经济学中“理性人”的假设。

（4）参与方承担的风险与所获收益成正比，以此激励参与方主动承担一定风险。

（5）参与方都不希望谈判破裂，并愿意为此做出妥协。

2.3 博弈过程描述

博弈三方根据自身情况提出已方的风险承担比例，构成初始策略。由于各方都是“理性人”，该初始策略是各自承担风险的最小值，必然不能将风险完全分担，因此博弈继续。风险与收益成正比且都不希望谈判破裂，意味着参与方有承担能力范围内更多风险的动力。已方根据自身策略和能够体谅另外两方的程度调整承担比例，形成新的三方分配策略，如此循环进行。各参与方由于地位、实力、风险偏好等因素的不同，风险承受能力有一定差异，但都有各自承担风险能力的最大极限，该极限即为合作博弈中的谈判破裂点。当各方风险都在承受范围之内且风险完全被分担时，博弈达到均衡，三方按照最终策略各自承担相应风险。

2.4 模型的构建与求解

2.4.1 模型的建立

所谓三方相互体谅，就是基于经济学中的适应性预期理论，各方在提出每轮策略时，体谅另外两方的诉求，根据适应性预期调整己方下一轮策略。

适应性预期模型是经济学中的一个经典模型。分别用En和Rn来表示第n轮的预期值和实际值，用β表示适应系数，也可称为妥协系数，表示某方能够体谅他方并妥协的程度。该模型表示为：

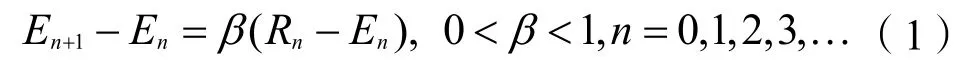
模型中0＜β＜1表示预期的调整（En+1-En）是对预期与实际偏差（Rn-En）的部分调整，且调整幅度小于偏差幅度。式（1）经变换可得：

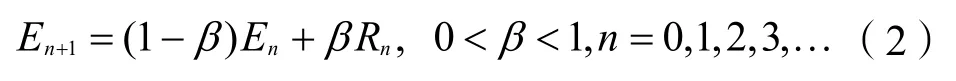
由式（2）可看出，下一轮预期值与本轮预期值和本轮实际值有关。

对于遵循相互体谅原则进行讨价还价的三方，可以在适应性预期模型基础上建立三方相互体谅的讨价还价博弈模型。以Y代表业主方、Z代表全过程咨询方、S代表施工方，设所需分担的风险总量为1。博弈开始，Y、Z、S首先提出己方愿意主动承担的风险比例Y0，Z0，S0，构成初始策略。由于初始策略不能将风险完全分担，故必有下式：

此时博弈不能达成均衡，所以进入下一回合时各方需对其初始策略进行调整，形成新的策略。博弈三方在第n轮提出的己方承担的风险比例用Yn，Zn，Sn表示，也就是预期值。同时，三方策略组合起来又共同形成第n轮各方的实际值。因为风险总量1是给定的，按照第n轮咨询方与施工方给出的策略Zn和Sn，业主方实际需承担的风险量为1-Zn-Sn。分别用βY、βZ、βS表示业主方、全过程咨询方和施工方的适应系数。以业主方为例，如业主体谅全过程咨询方及施工方诉求，则其下一轮策略将按照适应性预期模型做出调整，即：Yn+1=(1-βY)Yn

+βY(1-Zn-Sn)。同理可得全过程咨询方与施工方的下一轮策略Zn+1和Sn+1。由此便得到三方相互体谅的讨价还价模型：

2.4.2 模型的求解

参与方都希望尽可能达成合作并为此做出让步，但各方均有其承受能力的极限，若超过极限则谈判破裂。设业主方、全过程咨询方、施工方的承受极限为Ymax、Zmax、Smax，则三方讨价还价成功达成合作且风险完全分担的前提是三方的最大承受能力之和不小于风险总量。

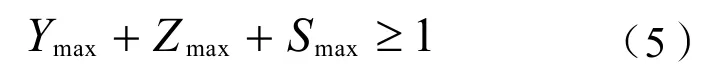
三方相互体谅的讨价还价模型经过变换可转为如下形式：

有一种特殊情况，是三方的适应系数恰好等于1。令式（6）中n=0并将三式相加得Y1+Z1+S1=1。也就是说，三方只经过一个回合就可以将风险完全分担，达成博弈均衡。

但在一般情况下，三方的适应系数并不能恰好互补，βY+βZ+βS≠1。将式（6）中的3个等式相加得：

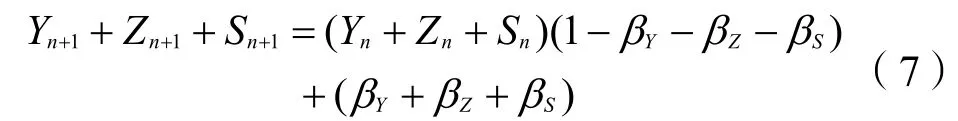
式（7）表明，在0＜βY+βZ+βS＜1的条件下，各轮讨价还价中三方风险比例之和是由上一轮风险比例之和与风险总量1的加权平均数，权重分别为1-βY-βZ-βS和βY+βZ+βS。而0＜βY+βZ+βS＜1反映了三方总的妥协程度不高，体现了各方在承担重要风险时，都为了自身利益而采取较为谨慎的调整策略。

按照常识判断，要使三方讨价还价博弈达到均衡，各方需根据己方既有策略和另外两方的策略，逐轮提高自己的风险承担比例，提高的程度由适应系数来体现。结合式（3）和式（7）可知Y1+Z1+S1＜1，递推下去得：

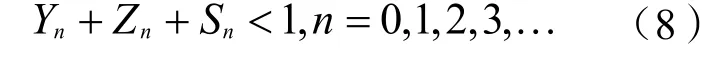
式（8）的含义是在达成均衡前各轮次被分担风险之和小于风险总量。由式（6）和式（8）分析得：

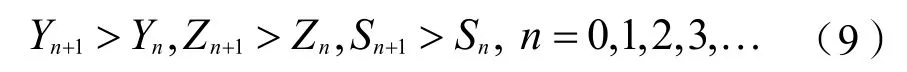
式（9）表明Y、Z、S三方逐轮次给出的风险分担量形成的数列{Yn}，{Zn}，{Sn}都是严格单调递增数列。因为各方都有其承受极限Ymax，Zmax，Smax，它们就构成对应数列的上界。根据单调有界数列极限存在定理，数列{Yn}，{Zn}，{Sn}严格单调递增且有上界，必然存在极限，记为Y*、Z*、S*。

三方相互体谅的讨价还价博弈模型式（4）可改写为：

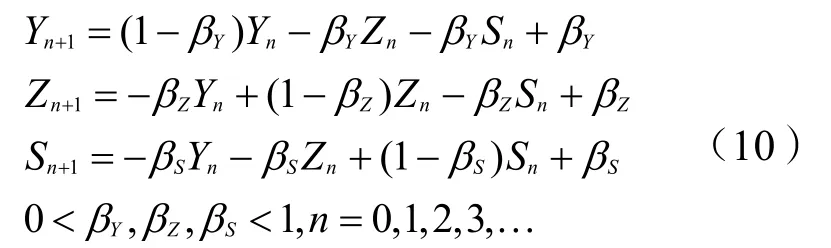
由差分方程理论可看出，模型式（10）是一个三元常系数非齐次线性差分方程组。当式中Yn=Y*，Zn=Z*，Sn=S*时，下一轮讨价还价的结果依然是Yn+1=Y*，Zn+1=Z*，Sn+1=S*。此时将3个等式相加可得Y*+Z*+S*=1，说明Y*、Z*、S*作为差分方程组的解能够使模型式（4）表示的三方相互体谅讨价还价博弈达到均衡，即Y*、Z*、S*是方程组的特解。

就三方讨价还价模型来说，各方提出的初始策略Y0，Z0，S0就是差分方程组式（10）的初始值。三方博弈达成均衡就是求差分方程组式（10）在初始条件Y0，Z0，S0下的解。已知存在的Y*、Z*、S*是方程组的一个特解，根据差分方程组求解定理，方程组式（10）具有唯一解。可利用特解Y*、Z*、S*和式（10）去掉常数项后的常系数齐次线性差分方程组的通解求得式（10）在初始条件Y0，Z0，S0下的解。

首先需求解式（10）去掉常数项后的常系数齐次线性差分方程组的特征值。用A表示Yn，Zn，Sn的系数矩阵，行列式|λI-A|是系数矩阵A的特征多项式。

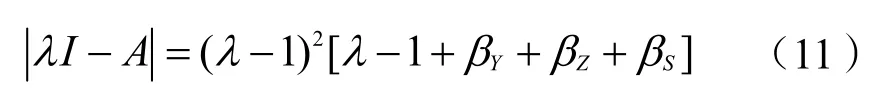
经计算，矩阵A的特征值为1和1-βY-βZ-βS，其中1是双重特征值，对应的特征向量分别为（1，-1，0)T，(0，1，-1)T，特征值1-βY-βZ-βS对应的特征向量为(βY，βZ，βS)T。将以上3个特征值及其对应的特征向量、特解代入常系数线性差分方程组通解公式，便得到不考虑初始值时非齐次线性差分方程组（10）的通解。

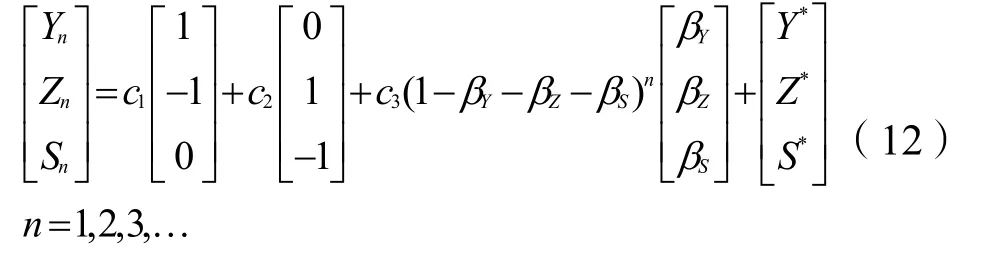
式（12）中c1，c2，c3为任意常数，但在初始值Y0，Z0，S0下它们是唯一的。运用待定系数法将式（10）与式（12）联立求解可得：

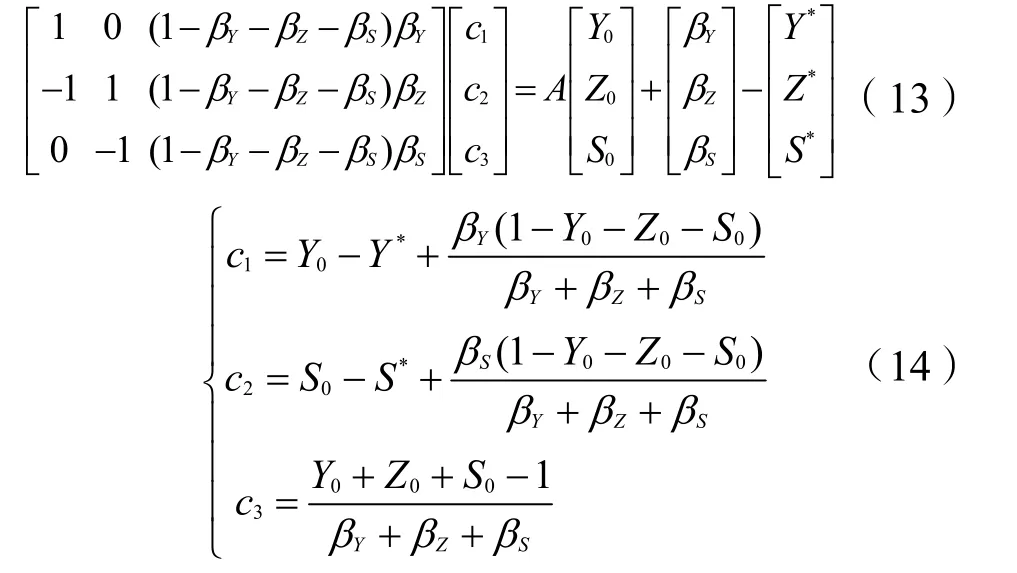
将式（14）代入式（12）便可求得差分方程组（10）在初始值Y0，Z0，S0下的唯一解。用X表示业主方、全过程咨询方、施工方中的任意一方，X的取值为Y、Z、S。那么，唯一解的通式如下：

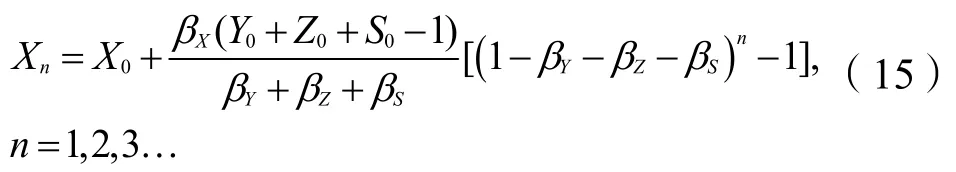
式（15）是各方逐轮次风险分担量数列{Yn}， {Zn}，{Sn}的通项，揭示了各方如何在讨价还价中通过三方适应系数及己方初始值给出本轮策略。当博弈循环往复，直至达到均衡，即对式（15）求极限可得：

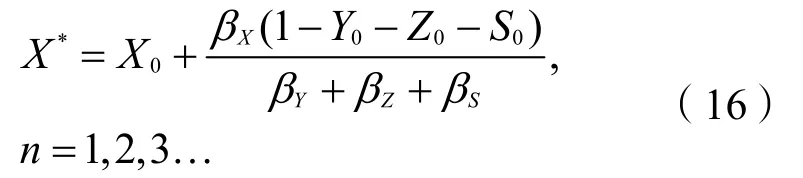
式（16）所示的各参与方策略即三方相互体谅的讨价还价博弈的纳什均衡解，该博弈完整的讨价还价过程如图2所示。

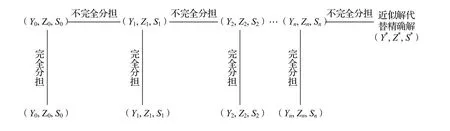
图2 三方相互体谅讨价还价博弈树

2.4.3 结果分析

以上模型给出了各参与方讨价还价的过程及唯一纳什均衡解，影响该分配结果的变量只有各方初始策略及适应系数，并且该结果充分尊重了各方意愿，有利于IPD团队合作关系的健康稳定发展。需注意的是，三方相互体谅讨价还价博弈模型中各参与方的适应系数是己方机密，所以博弈开始时，各方只能简单地按照式（4）调整己方策略进行讨价还价，循环往复，直至达到式（16）所示均衡，该博弈属于不完全信息下的无限重复合作博弈。

各参与方的适应系数由其专业知识水平和经验程度决定[17]。参照不完全信息下三方相互威慑讨价还价模型中折损因子[18]的定义结合无限博弈面临折现问题的特征，参与方在确定己方适应系数时需综合考虑自身风险承受能力范围、谈判损耗、折现因子、机会成本、时间成本、耐心等因素。

IPD模式与三方相互体谅讨价还价模型虽然都强调各方相互尊重，平等合作，但实际操作中三方的相对地位是不能完全相同的。各方适应系数的大小就代表了其向他方妥协的程度，适应系数越小且初始值越低，表示相对地位越高的参与方向他方妥协程度越低，且利用其地位便利承担更少的风险。假如三方地位绝对平等，那么各方初始策略和适应系数则完全相同，风险分担比例为各承担1/3。

在模型的求解过程中，纳什均衡结果由精确解求极限所得的近似解表示，在实际博弈过程中，无限博弈是不实际的，需耗费大量时间和资源，与IPD模式的初衷相悖。故该模型应用到工程实际时，三方在博弈轮次达到一定数量或策略调整幅度较小时应共同协商，以近似解代替精确解，及时停止谈判，减少不必要的成本支出，共同为项目顺利有效开展让利。但三方不可事先约定谈判期限，否则该博弈将转化为有限博弈，纳什均衡随之改变。

3 工程算例

在国内市场，IPD模式目前仍处于概念探索阶段，实践案例十分稀少。假设某公路工程建设项目采用IPD模式，在风险分担中各参与方初始策略及适应系数如表1所示。

表1 各参与方基础数据

现按照适应性预期调整博弈策略，三方博弈过程如下：

第一回合：业主、全过程咨询方、施工方提出各自愿意承担的风险比例分别为：Y0=0.3，Z0=0.2，S0=0.3，由于风险未被完全分担，谈判继续。

如此循环进行，博弈过程中各方策略变化及最终结果如图3所示。

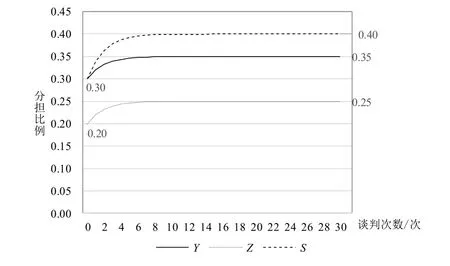
图3 算例博弈过程模拟

由图3可看出，业主方、全过程咨询方、施工方经过多轮谈判后各方承担的风险比例分别为：35%，25%，40%。将基础数据代入式（16）可得出相同结论，验证了三方相互体谅讨价还价模型的 可靠性。

博弈策略在前几轮调整幅度较大，随着谈判轮次的增加逐渐趋于平稳。因此，在工程实际中，当谈判继续进行但各方调整幅度较小时，三方可协商以近似值为最终策略而终止谈判，降低谈判成本。以三方完全对等，各承担33.3%为风险基准线，此分配结果较为均衡，避免了传统交付模式下参与方地位不平等带来的某方被迫承担过多风险的弊端，更有利于合作关系的稳定，因此具有一定合理性。

4 结语

本文以IPD模式为研究背景，针对公路工程建设项目中需三方共同承担的风险分担问题，构建了基于适应性预期的三方相互体谅讨价还价模型。各方在初始策略下，体谅另外两方的诉求，根据适应性预期调整己方下一轮策略，进行不完全信息下无限重复博弈，直至达到纳什均衡。影响风险分担结果的变量只有初始策略与适应系数。适应系数β包含了自身风险承受能力范围、谈判损耗、折现因子、机会成本、时间成本、耐心等因素。

通过一个工程算例对三方相互体谅讨价还价博弈过程及结果进行展示，验证了模型的可靠性。该模型应用到工程实际时，三方在博弈轮次达到一定数量或策略调整幅度较小时应共同协商，以近似解代替精确解，及时停止谈判。但三方不可事先约定谈判期限，否则该博弈将转化为有限博弈，纳什均衡随之改变。三方相互体谅讨价还价的风险分配方法充分尊重各方意愿，三方友好谈判、公平博弈，有利于IPD团队合作关系的健康稳定发展，从而促进IPD项目顺利实施。本文为IPD模式下的风险分担问题提供了新方法，该方法参数少，博弈过程简洁，应用较为方便。在应用过程中，适应系数对分配结果的影响重大，需综合考虑多种因素的作用。因此，如何评估确定各参与方的适应系数是下一步研究的重点。