施工方参与回购的建筑供应链协调及应急策略

陈若禺，朱莉

(1.华南理工大学 电子商务系，广东 广州 510006；2.南京信息工程大学 管理工程学院，江苏 南京 210044)

建筑供应链是一种典型按订单制造的供应链，是由业主需求驱动、以业主为核心，供应商、施工方以及业主等围绕单个或多个建设项目组成的一个功能性网链结构[1]。由于建筑行业特点和生产建设要求，通常采取招标等形式来确定供应链上各主体成员，即建筑供应链上各成员关系的维系很大程度上依赖于契约协调机制[2]。目前，契约理论应用到的供应链情境更多。设置有效的各类契约以实现建筑供应链的优化是契约理论新发展的体现，也拥有众多研究成果，杨红雄等[3]解决了建筑供应链中承包商风险厌恶的数量弹性契约设计问题。ZHAΙ等[4]采用风险成本共担机制来解决建筑供应链中对生产提前期的规避问题。LΙU等[5]提倡运用最小数量承诺契约合同来应对建筑供应链的不确定性。各种经典供应链契约的有效应用对整个建筑供应链利润的提高以及风险的控制均起到重要推动作用。本文拟探讨回购契约在建筑供应链中的应用。回购契约是指在销售季节末，供应链上游供应商对下游企业未卖出的过剩产品以约定的、小于批发价的价格进行回购的契约。这个将销售剩余产品回购的协调理念由PASTERNACK[6]率先提出，后续引起许多学者的关注，如SONG等[7]研究了一个在Stackelberg框架下生产商与销售商间合理定价的回购契约协调机制。近年来，回购契约与供应链成员的风险偏好结合的越来越多。代建生等[8]分析了销售商风险规避情形下集中式和分散式供应链中回购契约的差异，讨论了供应链成员不同的风险态度对契约设计和整个供应链收益的影响。于春海等[9]根据零售商风险厌恶程度，构建了考虑风险参数和均值-CVaR决策准则的二级闭环供应链回购契约决策模型。陈胜利等[10]研究了市场需求和供应商单位生产成本同时扰动情形下如何设计风险厌恶型供应链回购契约的问题。也有将回购与其他契约进行比较或结合的研究，如简惠云等[11]通过对比批发价格契约与回购契约，发现风险规避型的供应链在博弈时更易选择回购契约。组合契约及改进契约因其可弥补原有契约的不足成为契约理论研究新趋势，刘岱[12]比较了各类契约对农产品新鲜度及供应链的影响，找到了维持供应链稳定的较有效的契约方式。赵亮等[13]发现改进收益共享契约和回购联合契约对双渠道供应链有较好的协调作用。还有不少文献讨论回购契约如何协调突发事件下的供应链。如于辉等[14-15]提倡通过调整回购契约中批发价格，以保持突发事件下供应链的顺利运转。不同于回购契约在一般制造业供应链中的协调应用，本文聚焦建筑行业中由材料供应商与下游施工方组成的典型二级供应链。针对建筑行业材料订单制造的特性，突破上下游企业间的传统回购模式，提出同层级施工方参与回购的创新契约协调策略，并构建相应的施工方参与回购的建筑供应链契约协调定量模型。本文探讨与传统供应商回购模式相比，施工方参与回购的协调机制是否能够有效提升由单施工方和单供应商组成的原二级建筑供应链利润，以及当遭遇突发事件扰动时，2种回购契约模式下回购价格和批发价格如何调整才能使建筑供应链恢复顺利运转等问题。

1 常态下二级建筑供应链回购契约模型

1.1 传统回购契约模型

采用传统回购契约模型的二级建筑供应链由单供应商和单施工方组成，契约签订及执行过程如图1。与于刚等[14-15]假设一致：供应链上成员均理性和风险中性，均按各自利润最大化进行决策；各成员间相互知晓对方收益函数、成本结构等；且各供应链成员对市场需求的分布均可准确预测。

图1 传统二级建筑供应链回购契约签订、执行过程Fig.1 Signing and execution process of repurchase contract of traditional secondary building supply chain

设p为施工方耗用每单位建材从业主处所获的支付，是一个外生变量即固定常数，由建材产品市场竞争状况决定；cs是供应商处每单位建材的供应成本；cf为施工方处除购买以外的单位边际成本(如清点验货成本等)，记c=cs+cf，设p＞c；gs和gf是每单位建材缺货而分别致供应商和施工方的损失成本，记g=gs+gf；v为单位建材产品的残值；w是施工方从供应商处购买单位建材产品的批发价格；b为供应商提供给施工方单位建材产品的回购价格(可理解为建筑工程项目结束后，供应商对施工方剩余建材提供的一种价格补贴)。令回购价格需大于产品残值、且施工方不能从产品剩余中获利，即p＞w＞b＞v，v+b≤w。

q为某种建材产品订货量；D是施工方面临的某种建材产品需求，其分布函数F(x)，概率密度f(x)；F(x)可微且严格递增，有F(0)=0，-F(x)=1-F(x)；记μ=E(D)是期望需求。订货量为q时施工方处所耗建材的期望值为建筑工程项目结束后施工方处建材剩余数量的期望值为I(q)=q-S(q)，建材缺货数量的期望值为L(q)=μ-S(q)。供应商与施工方明确采取回购契约的转移支付为T(q,w,b)=wq-bI(q)。

采用传统回购契约，施工方、供应商以及二级供应链总的期望收益函数分别表达如下：

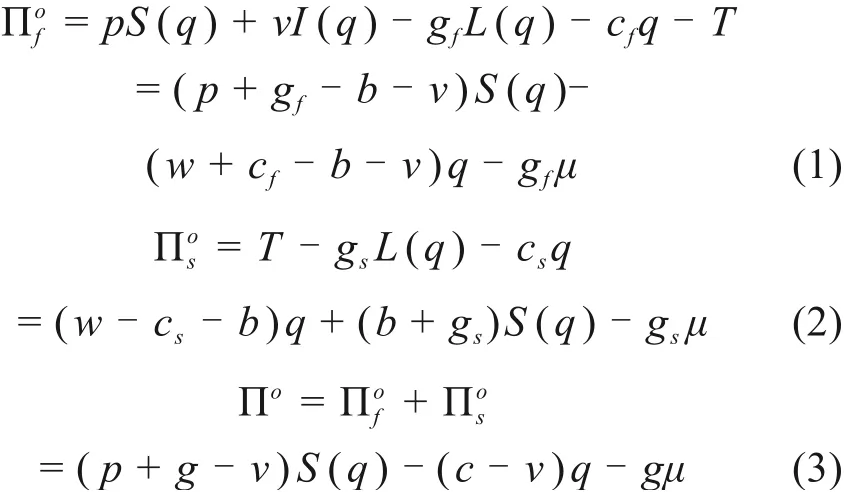
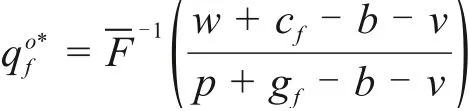
令(Πo)′=0，得传统回购契约下整个二级供应链系统决定的最优订货量为：

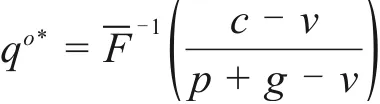
由于需求分布函数F(x)单调递增，故存在唯一的最优订货量。即二级建筑供应链协调时，施工方的最优订货量qo*f必须等于供应链系统最优订货量qo*。故为实现整个供应链的协调，传统回购契约中批发价格和回购价格这2个关键参数(w,b)，对于任意δo≥0(δo为分配整个二级供应链利润的系统契约参数)需满足下式[14]：

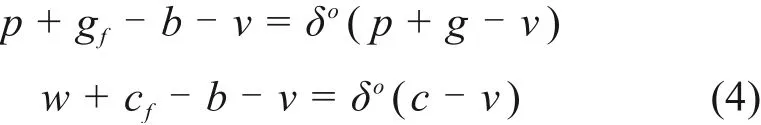
将式(4)代入式(1)，有

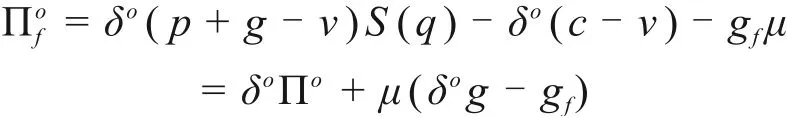
1.2 施工方参与回购的契约模型

由于建筑供应链中材料按订单制造的特性，一种建材(如钢轨)只适用于特定类型的建筑工程项目。当某种建材剩余时，除了可被上游供应商回收外，还可利用的途径就是被其他同类型建筑工程的施工方回收使用，如此便可能出现同层级其他施工方与上游供应商共同回购剩余建材的现象。故在契约执行阶段本文提出同层级其他施工方共同参与剩余建材回购的协调模式。

图2 施工方参与回购的契约执行阶段Fig.2 Construction party participates in the contract execution stage of repurchase

将传统回购契约中的原施工方和拟参与回购的其他施工方分别记作A和B，其收益函数的符号表达也均用下标A和B以作区分。施工方参与回购的契约运作机制如下：若施工方A在某建筑工程项目结束后仍有剩余建材，供应商可实施回购(仍指提供回购价格补贴)的比例为1-φ，承担同类型建筑工程的其他施工方B参与回购的比例为φ(0＜φ＜1)。在此契约模式下，施工方B可被视为一个外来者，只参与回收环节。为便于建模，设施工方B回购一定建材后不存在剩余，且施工方B耗用每单位建材所获的支付价格也为p，假设施工方B与上游供应商提供给施工方A的单位建材回购价格相同、均用b表示，施工方B参与回购建材需付出一定成本(如运输成本)用cfB表示。

施工方参与回购的契约模式下，施工方A，施工方B以及供应商的期望收益函数分别为：

施工方参与回购的契约模式下，整个建筑供应链总的期望收益函数为：

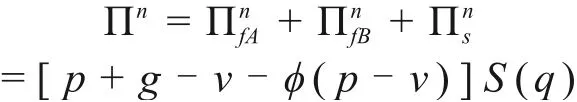
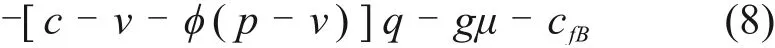
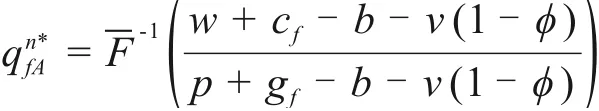
令(Πn)′=0，得施工方参与回购契约模式下整个建筑供应链系统决定的最优订货量为：

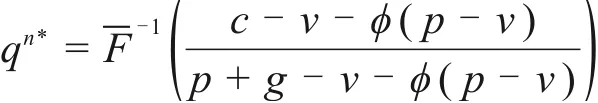
同样由于分布函数F单调递增，存在唯一的最优订货量。故在施工方参与回购的契约协调时施工方A最优订货量qn*fA需等于建筑供应链系统最优订货量qn*，此时契约中2个关键参数(w,b)，对于任意δn≥0需满足下式：

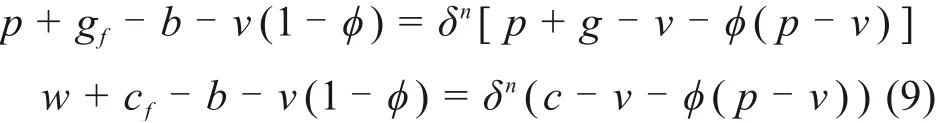
将式(9)代入式(5)，有

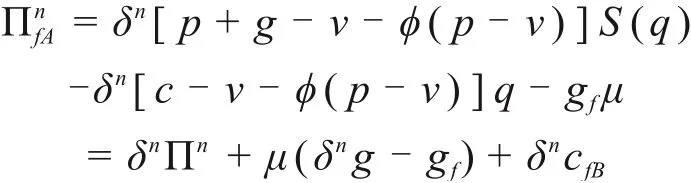
可见施工方A的期望收益函数与供应链总期望收益函数之间形成了仿射函数[14]，故此时施工方A的最优订货量等于整个建筑供应链系统最优订货量qn*，且可通过调整δn分配供应链收益，使之达到协调。可见施工方参与回购的契约对由供应商、施工方A和施工方B组成的整个建筑供应链系统具有协调作用。

通过对比施工方参与回购契约和传统回购契约的二级供应链期望收益可得以下命题：

【命题1】在不考虑突发事件的常态交易下，与传统回购契约相比，施工方B参与回购的契约模式能够提升由供应商和施工方A组成的原二级建筑供应链期望收益。

【证明】将式(5)与式(7)相加，得施工方B参与回购的契约模式下，施工方A与供应商的期望收益之和为：

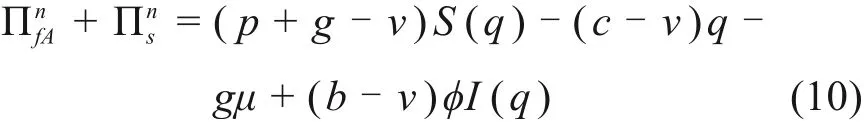
由于b＞v，则(b-v)φI(q)＞0，故式(10)大于式(3)，即施工方参与回购的契约模式使得供应商和施工方A组成的原二级建筑供应链期望收益增加。

2 突发事件下二级建筑供应链回购契约模型及应急策略

在实际施工过程中，会因为业主要求变化而产生设计变更，从而导致某种建材的需求突然增大或减少。当建筑供应链面对突发事件扰动时，假设建材产品需求的分布函数由F(x)变为M(x)，概率密度函数由f(x)变为m(x)；M(x)仍为可微且严格递增期望需求为μm=Em(D)；供应链中施工方所耗建材的期望值变为建筑工程项目结束后该施工方处建材剩余数量的期望值及缺货数量的期望值分别为Im(q)=q-Sm(q)和Lm(q)=μm-Sm(q)。为便于量化突发事件的影响，假设建材产品无论需求增大或减少均对供应商造成一定困扰，分别导致供应商增加的单位应对成本用λ1和λ2来表示。现分别讨论突发事件下传统回购契约及同层施工方参与回购契约的应急策略。

2.1 传统回购契约模型的应急策略

突发事件下采用传统回购契约的模式，施工方、供应商以及二级供应链总的期望收益函数分别为：

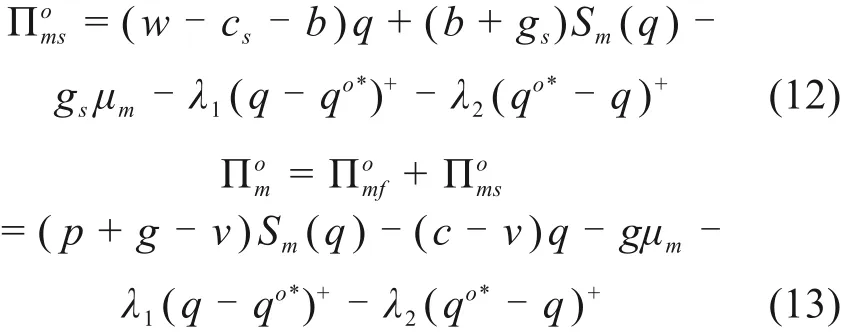
在遭遇突发事件后，由式(4)，式(11)和式(13)可推出施工方期望收益函数与供应链总期望收益函数的关系为：

此时施工方的期望收益函数未能与供应链总期望收益函数之间形成仿射关系，二级建筑供应链不再协调。

若将传统回购契约中的批发价格和回购价格分别做如下调整[15]：

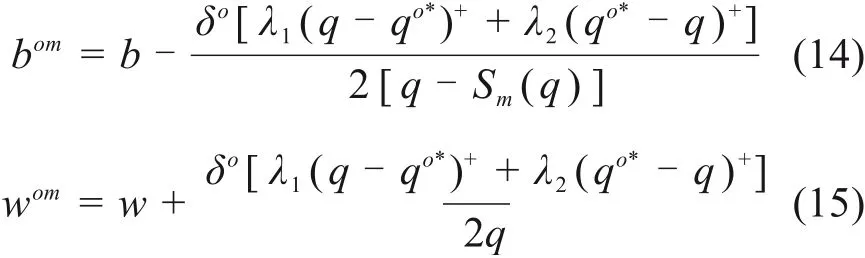
结合式(4)，且将调整后的批发价格和回购价格(14)～(15)代入施工方期望收益函数(11)得：

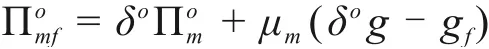
发现施工方的期望收益函数与供应链总期望收益函数之间再次形成仿射函数，二级建筑供应链重新达到协调。

2.2 施工方参与回购契约模型的应急策略

突发事件下采用施工方参与回购的契约模式，施工方A，施工方B以及供应商的期望收益函数分别表示为：

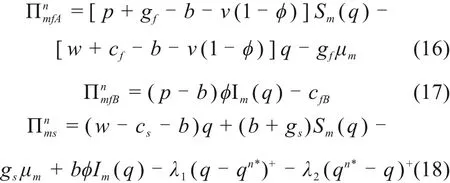
突发事件下采用施工方参与回购的契约模式，整个建筑供应链总的期望收益函数为：

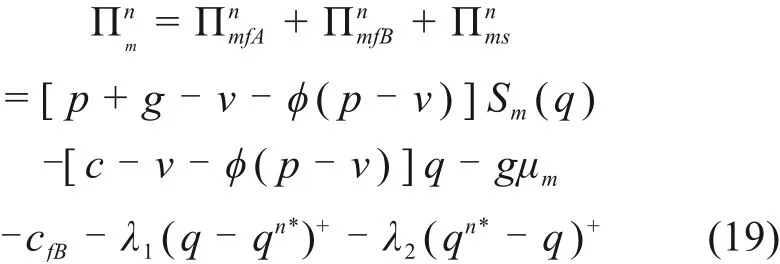
由式(9)，式(16)和式(19)可推出，施工方A的期望收益函数与供应链总期望收益函数的关系式为：

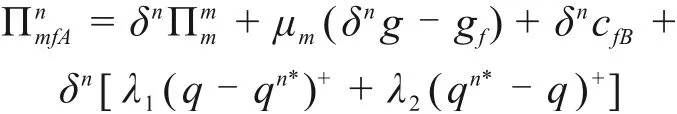
可见施工方A的期望收益函数未能与供应链总期望收益函数之间形成仿射关系，整个建筑供应链系统不再协调。

若将施工方参与回购契约中批发价格和回购价格分别做如下调整：

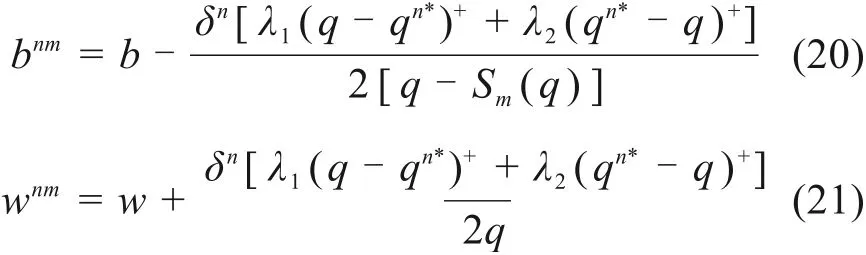
由式(9)，并将调整后的批发价格和回购价格(20)～(21)代入施工方A期望收益函数(16)，得：

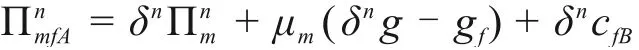
发现施工方A期望收益函数与供应链总期望收益函数之间再次形成仿射函数，整个建筑供应链系统重新达到协调。

通过对比突发事件导致需求突然增大情形下传统回购契约与施工方参与回购契约最优订货量的对比可得到命题2。

【命题2】突发事件的发生导致需求突然增大时，与传统回购契约相比，施工方参与回购契约协调建筑供应链时呈现更低的应急应对成本。

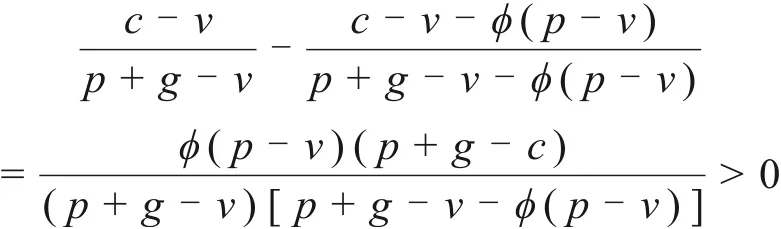
由于F(x)是严格递增函数，有：

鉴于F-1(x)为F(x)的反函数，两者单调性相同，得出qo*＜qn*，即施工方参与回购契约下供应链最优订货量大于传统回购契约下供应链最优订货量。因此，当突发事件的发生导致需求突然增大时，2种回购契约下对供应商造成的应对成本有λ1(qqo*)+＞λ1(q-qn*)+，即施工方参与回购契约为建筑供应链带来更低的应急应对成本。

3 算例分析

3.1 算例场景

2016年，中铁十二局集团修建渝黔铁路时，A项目部闲置43号钢轨约25 t，该型号钢轨采购批发价为5 400元/t。若将闲置钢轨进行库存保存会产生大量保管费用，钢轨可能会因长期存放而被锈蚀；若将钢轨作为废品处理，其处理价格为1 900元/t。后经信息交流获知B项目部需要此型号钢轨，经A和B双方磋商，最终A以2 900元/t的价格出售给B项目部一部分闲置钢轨。此外，由于A项目部欠上游供应商一定资金，为免遭起诉，A项目部与供应商经友好协商后同样以2 900元/t的价格将剩余的闲置钢轨抵押给供应商作为资金还款。

依托此中铁十二局集团修建铁路项目的案例背景，结合调研有如下相关参数：每吨钢轨的批发价格为w=5 400元；每吨钢轨的供应商和施工方回购价格均为b=2 900元；每吨闲置钢轨的残值v=1 900元；耗用每吨钢轨业主给施工方A和B的价格支付均为p=6 000元。施工方A拥有每吨钢轨所需付出的清点验货成本cf=200元；供应商处每吨钢轨的供应成本cs=3 240元；施工方B参与钢轨回购所耗的成本cfB=3 500元；每缺货1 t钢轨而致使供应商和施工方产生的损失成本为gs=gf=1 000元。施工方B参与钢轨回购的比例为φ=0.5。常态情形下钢轨需求D服从正态分布N(200,52)；若突发事件导致需求量增加，需求变为N(250,52)，增加每吨钢轨需求对供应商造成的应对成本为λ1=500元；若突发事件致使需求量减少，此时需求服从N(150,52)，减少每吨钢轨需求致供应商处应对成本λ2=550元。

3.2 结果对比与参数分析

在MATLAB R2015b中实现上述中铁十二局集团修建铁路项目的算例场景，得出传统回购和施工方参与回购2种契约模式下的协调及应急策略。通过结果对比发现：未发生突发事件的常态下施工方参与回购契约下供应商和施工方两者期望收益之和为468 130元，比传统回购契约协调下预期所获的460 663元高出16.2‰；而针对突发事件发生时所需花费的应急应对总成本，施工方参与的回购契约比传统回购契约节省约1个百分点(52 325元v.s.52 935元)，其中采用施工方参与的回购契约在建材需求突然增大时所需付出的应对协调成本更是少了5 000元。这说明在中铁十二局集团修建铁路算例背景下，本文所提出的施工方参与回购契约模式比传统回购契约更具优势。

现对施工方参与回购契约中的重要参数φ(施工方B参与回购的比例)实施敏感性分析，观察其变化对该回购契约所具优势的影响。图3表明从0到1改变φ值时，常态下2种回购契约模式的供应商与施工方期望收益之和(图3(a))、以及突发事件下整个建筑供应链所需付出应急应对成本(图3(b))的对比变化情况。发现不论参与回购比例如何变化，本文所提出的施工方参与回购契约具有稳定优势，且施工方B参与回购的比例越大，这种协调优势愈加明显。

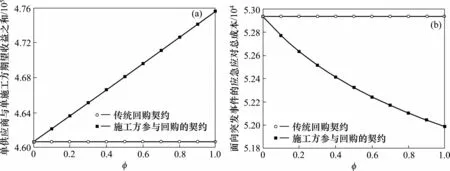
图3 不同比例φ下传统回购契约与施工方参与回购契约的比较Fig.3 Comparison of traditional repurchase contract and builder’s participation in repurchase contract under different proportionsφ

最后，进一步讨论施工方B愿意参与回购的前提条件，对与施工方B期望收益相关的重要参数b和φ实施敏感性分析，即观察b和φ的变化对施工方B期望收益的影响，结果见表1。由表1可看出常态下，除了施工方B完全不参与回购的情形，当参与回购的比例φ位于区间[0.1,0.2]时，施工方B所获期望收益会历经扭亏为盈(由负到正)的变化。具体地，发现当φ在0.17值附近时，施工方B的期望收益趋近于0。即仅当φ≥0.17时，施工方B才有意愿和动力参与回购活动，施工方参与回购契约这种协调模式才能得以真正实施；否则施工方B将会选择直接向供应商购买建材。此外，表1的数据还显示，回购价格越低、参与回购比例越高时，施工方B的期望收益越大。极端情形时，完全由施工方B承担闲置钢轨的回购(φ=1)，且回购价格与残值相等(b=1 900)时，施工方B期望收益升至最高，鉴于b＞v，故施工方B期望收益最高只能接近29 713元。这说明建筑供应链遭遇突发事件时，在某种程度上降低回购价格能使其他施工方更愿意参与到共同回购活动中来，以促进供应链顺利运转状态的恢复。

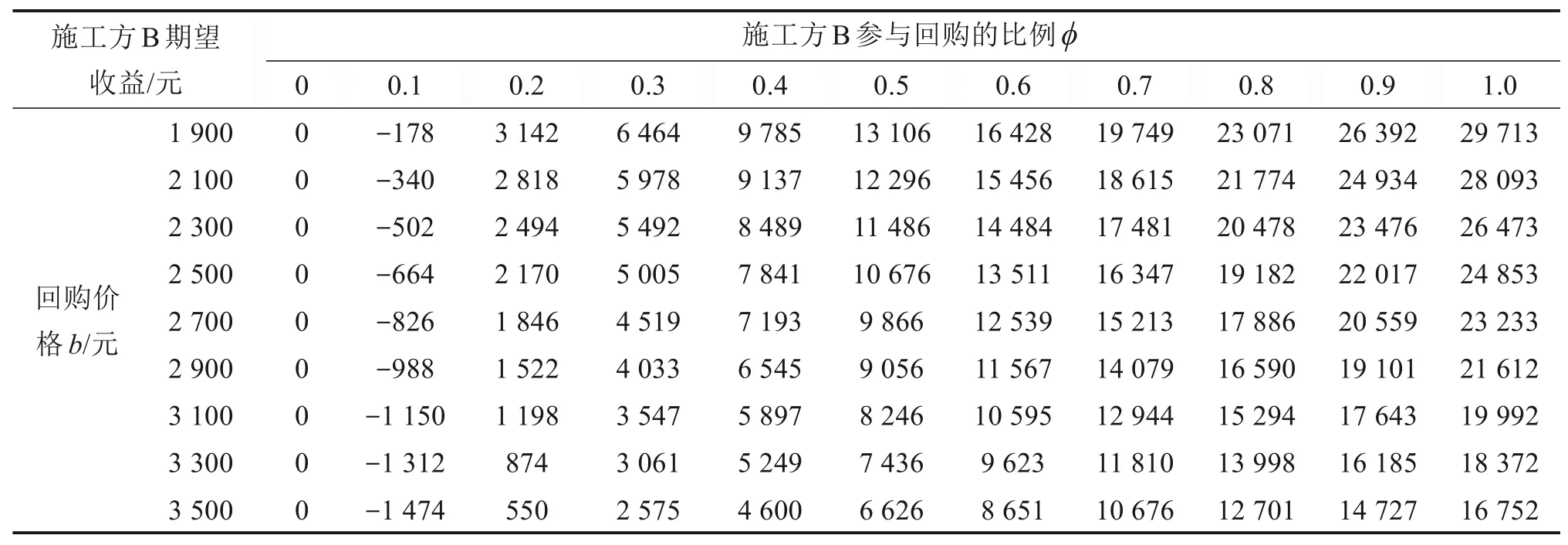
表1 回购价格b和回购比例φ对施工方B期望收益的影响Table 1 Ιnfluence of buyback price b and buyback ratioφon the expected earnings of builder B

4 结论

1)未发生突发事件的常态情形时，施工方参与回购契约协调所致的供应商和施工方原二级建筑供应链期望收益更高。

2)发生突发事件时，可通过合理调整回购价格和批发价格以使建筑供应链重新协调运作。

3)突发事件导致的需求增大情形时，施工方参与回购契约所耗的应急应对成本更低。

通过进一步对施工方参与的回购价格和回购比例实施敏感性分析，发现当2个关键参数满足一定前提条件时，所构造的施工方参与回购契约模式具有实际可行性和较稳定的优越性。契约模式的对比探讨和参数分析结果为相关管理部门制定合适高效的供应链协调机制提供有益参考。未来研究可尝试突破二级供应链背景，考虑工程中多层级建筑供应链运营场景。