高速铁路列车制动曲线计算精确度与效率分析

张友兵，王建敏，张国振，陈志强，吴培栋

(北京全路通信信号研究设计院集团有限公司 安全控制技术研究院，北京 100070)

高速铁路列车控制系统包括地面设备和车载设备，是保证高速铁路列车行车安全的核心系统。在列车运行过程中，车载设备根据行车许可、线路数据和列车制动参数计算目标距离连续速度控制模式曲线，对列车位置和速度进行实时监控，保证列车安全、高效运行。目前，我国高速铁路列车车载设备供应商主要采用欧标法和日立法2种简化算法计算制动曲线。欧标法采用基于速度的减速度模型，将制动减速度最多分为6段，在每个速度分段内使用固定减速度，从行车许可终点迭代逆推计算制动曲线[1]。在日立法中，车载设备存储了7档坡度下的制动距离表，将实际坡度信息归档到存储的坡度档位上，查找该坡度下的制动距离[2]。本文也采用欧标法计算制动曲线，但是突破制动减速度分为6段的局限性，研究如何对减速度进行合理分段，实现制动曲线计算精确度和计算效率的统一。本文主要介绍根据速度和位置对制动曲线进行分段的基本原理，给出根据速度分段计算制动曲线的方法，对方法进行建模和仿真实验，分析速度分段个数、等间隔分段和不等间隔分段、速度分段内制动减速度的选择策略对制动曲线计算结果精确度和计算效率的影响；综合考虑车载设备计算制动距离精度的各个影响因素，提出曲率分段和等间隔分段相结合的速度分段方法，并验证方法有效性。

1 高速铁路列车速度距离监控

在高速铁路列车运行过程中，地面设备向车载设备传输列车前方的线路数据、行车许可等控车信息，车载设备根据线路数据、行车许可和列车制动参数实时计算紧急制动降速曲线和常用制动降速曲线，进而推导出紧急制动干预曲线、常用制动干预曲线、报警曲线、允许速度曲线、指示曲线等速度监控曲线。车载设备根据这些速度监控曲线实时监控列车当前速度，列车当前速度超过报警曲线时，车载设备通过DMΙ输出报警信息，提示司机控制列车速度；列车当前速度超过常用制动干预曲线时，车载设备向列车输出最大常用制动，对列车进行降速，保证列车行车安全；列车当前速度超过紧急制动干预曲线时，车载设备向列车输出紧急制动，对列车进行降速，保证列车行车安全。因此车载设备精确且高效计算紧急制动降速曲线和常用制动降速曲线等制动曲线，是防止列车超速、越过行车许可终点的基础和关键。

制动曲线的计算既受列车制动性能影响，又受列车所在线路的坡度、黏着系数等线路数据影响，这些影响最终都体现在对列车制动减速度的影响[3]。

1.1 列车制动性能

不同列车具有不同的制动性能，且在不同速度下具有不同制动减速能力[4-5]。为了使用计算机计算列车的制动曲线，必然要对速度进行分段，相同速度分段内采用相同的制动减速度。对速度分段越多，计算制动曲线需要进行的运算越多，降低制动曲线的计算效率；对速度分段越少，计算制动曲线所采用的制动减速度与实际减速度偏差较大，降低制动曲线计算结果的精确度。当前国际主流的采用目标距离连续速度控制模式的列控系统中，其制动减速度模型均采用基于速度的分段式减速度模型[6]，如图1所示，例如按速度分段将车辆制动减速度分为6档，在每个速度分段内的制动减速度为固定值。

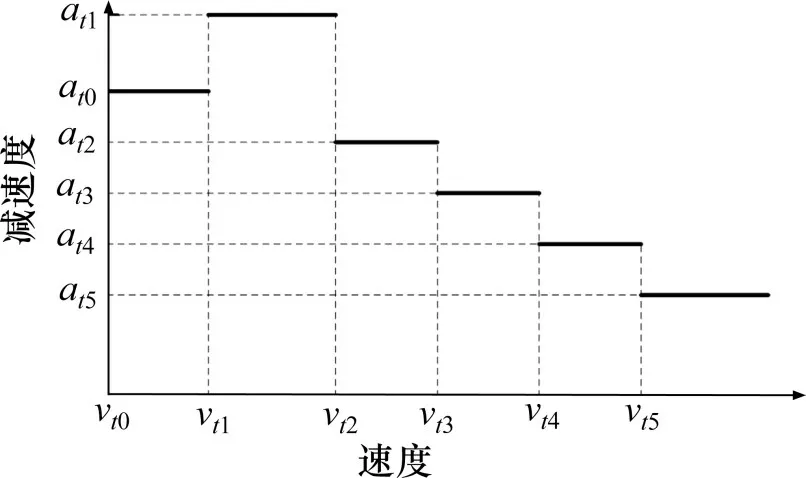
图1 基于速度的分段式减速度模型Fig.1 Deceleration model based on speed segment

1.2 线路坡度

因地形原因，高铁线路的不同位置具有不同的线路坡度。列车运行在上坡路段时，坡度体现为制动力。列车运行在下坡路段时，坡度体现为牵引力。因此，车载设备在计算制动曲线时，需要考虑线路坡度对列车制动减速度的影响，线路坡度变化点的两边具有不同的坡度值，因此需要根据坡度变化点对制动曲线进行分段。

1.3 线路黏着系数

在下雨天或下雪天，铁路轨道因为雨雪变得潮湿光滑，列车的制动能力降低。地面设备可以曲线数据的形式将光滑轨道信息发送给车载设备，光滑轨道信息包括起点位置和终点位置，即光滑轨道的范围。车载设备收到光滑轨道信息时，在光滑轨道范围内计算列车制动减速度时，需要在干轨条件下的列车制动减速度乘上黏着系数，一般情况下光滑轨道的黏着系数为0.7，即认为光滑轨道的列车制动减速度只有干轨的列车制动减速度的70%，以这种导向安全的方式保证列车行车安全。

2 制动曲线计算原理

2.1 制动曲线分段

在高速铁路列车控制系统中，车载设备根据行车许可和列车制动性能计算制动曲线。在计算制动曲线时，需要考虑列车前方行车许可范围内的坡度、光滑轨道等信息，还需要考虑列车在不能速度下的制动减速度。也就是说，制动曲线不但需要根据速度进行速度分段，还需要根据坡度变化点和黏着系数变化点进行距离分段[7]。

图2 为高速铁路列车制动曲线分段模型，位置d1是行车许可终点，d2和d4是坡度变化点，d5是光滑轨道起点，d3是光滑轨道终点，d6是列车当前位置。假设[d6,d4]，[d4,d2]，[d2,d1]范围内的坡度分别是grad1，grad2和grad3。

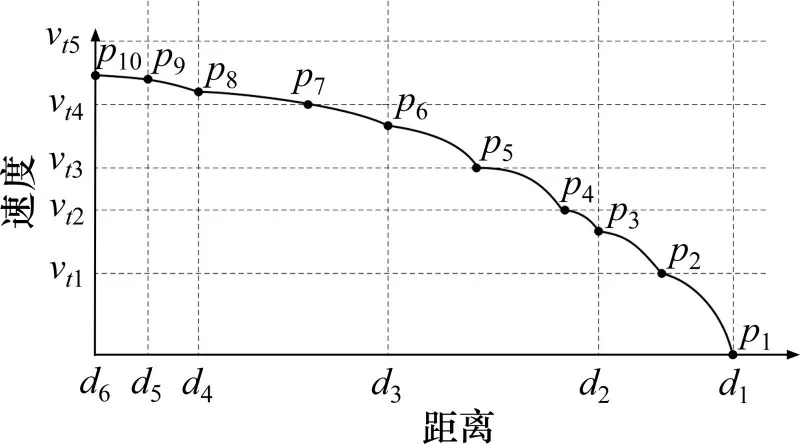
图2 高铁列车制动曲线分段模型Fig.2 Segmented model of braking curve of high-speed train

不同速度范围内的制动减速度不同，根据速度分段在制动曲线上分割出p2，p4，p5和p7共4个分割点。线路坡度影响制动减速度，坡度变化点在制动曲线上分割出p3点和p8点。线路黏着系数也影响制动减速度，黏着系数变化点在制动曲线上分割出p6点和p9点。此外，p1点是行车许可终点，p10点是列车当前位置。

2.2 速度分段内的车辆制动减速度

车辆提供的基本速度分段比较细致，一般5 km/h分为一段。而列控车载设备在计算制动曲线时，为了提高计算效率，并不是以5 km/h进行分段，而是以更大的速度步长进行分段，每个速度分段步长包括多个车辆提供的5 km/h基本分段制动减速度，所以车载设备需要确定将速度分段内的最小基本制动减速度作为该速度分段车辆的制动减速度，还是将速度分段内的所有基本制动减速度的平均值作为该速度分段车辆的制动减速度。假设一个速度分段包含n个基本制动减速度，分别为ab1，ab2，…，abn。

该速度分段车辆的最小制动减速度为：

该速度分段车辆的平均制动减速度为：

2.3 制动曲线各分段的综合制动减速度

以图2为例，根据速度和位置对制动曲线进行分段，在制动曲线上描绘出从p1到p10共10个制动曲线特征点。相邻2个特征点之间的制动减速度相同，如表1所示。例如，p1点和p2点之间具有相同的车辆制动减速度at0和相同的坡度grad3，所以p1点和p2点之间的综合制动减速度为at0+grad3。p6点和p7点之间具有相同的车辆制动减速度at3和相同的坡度grad2，且该范围内都是光滑轨道，黏着系数也在影响制动减速度，所以p6点和p7点之间的综合制动减速度为(at3+grad2)×adh。

表1 制动曲线各个分段的综合制动减速度Table 1 Comprehensive braking deceleration of each segment of braking curves

3 速度监控曲线计算方法

车载设备从列车停车点向列车当前位置递推，依次迭代逆推计算制动曲线上的所有特征点的(距离，速度)坐标，将所有特征点连接起来，得到列车制动曲线。如果制动曲线上的特征点因速度分段得到，特征点的速度已知，需要根据速度推算距离；如果制动曲线上的特征点因距离分段得到，特征点的位置已知，需要根据位置推算速度。

下面3个根据动能定理推导的列车运行方程将在使用欧标法计算制动曲线时发挥重要作用[8-11]：

3.1 根据速度推算距离

在已知前一个特征点的位置、前一个特征点的速度、当前特征点的速度时，根据式(4)可以计算当前特征点与前一个特征点的距离。在图2中，由p1点推算p2点，由p3点推算p4点，由p4点推算p5点，由p6点推算p7点，都是根据当前特征点的速度推算当前特征点的位置。

p1点的坐标为(sp1,vp1)，p2点的坐标为(sp2,vp2)，其中，p1点的位置sp1，p1点的速度vp1，p2点的速度vp2已知，p1点和p2点之间的综合制动减速度为固定值a step1=at0+grad3，根据式(4)可知，p2点与p1点的距离则p2点的位置为sp2=sp1-sp12。

3.2 根据距离推算速度

在已知前一个特征点的位置、前一个特征点的速度、当前特征点的位置时，根据式(5)计算当前特征点的速度，在图2中，由p2点推算p3点，由p5点推算p6点，由p7点推算p8点，由p8点推算p9点，由p9点推算p10点，都是根据当前特征点与前一个特征点的距离推算当前特征点的速度。

下面具体描述如何由p2点推算p3点。p2点的坐标为(sp2,vp2)，p3点的坐标为(sp3,vp3)，其中，p2点的位置sp2，p2点的速度vp2，p3点的位置sp3已知，p2点和p3点之间的综合制动减速度为固定值astep2=at1+grad3，根据式(5)可知，p3点的速度vp3=

3.3 列车制动距离

计算完列车制动曲线上所有特征点的(位置，速度)坐标，可以得到所有相邻特征点之间的距离，根据式(6)对所有相邻特征点之间距离求和，得到列车制动距离。

4 制动曲线建模与仿真

4.1 制动曲线建模

在实际情况中，车载设备对列车施加制动后，由于存在制动延时，列车制动系统不会立即响应车载设备的制动命令。由于本文主要研究速度分段对制动曲线计算的影响，所以对列车制动过程进行简化，假设车载设备输出制动命令后，列车制动系统立即响应制动命令。

制动曲线计算过程如下：

根据速度和位置进行分段，得到制动曲线上的所有特征点。需要综合考虑该速度下的车辆制动减速度、线路坡度、线路黏着系数等因素，计算制动曲线每一个特征点的综合制动减速度。

确定速度分段内的车辆制动减速度选择策略，根据式(1)计算速度分段内车辆的最小制动减速度，或根据式(2)计算速度分段内车辆的平均制动减速度。

根据速度分段内的车辆制动减速度、坡度信息、黏着系数，使用式(3)计算每个速度分段内的综合制动减速度。

从行车许可终点向列车当前位置递推，依次计算制动曲线所有特征点的(位置，速度)坐标。如果当前特征点的速度已知，根据式(4)计算当前特征点与前一个特征点的距离，从而得到当前特征点的(位置，速度)坐标。

如果当前特征点位置已知，根据式(5)计算当前特征点的速度，从而得到当前特征点的(位置，速度)坐标。

计算完制动曲线上所有特征点的(位置，速度)坐标，所有特征点构成了列车制动曲线的准确轮廓，根据式(6)计算列车制动距离。

4.2 速度分段方式对精度和效率的影响

本文采用CRH380AL新一代(16编组)动车组车辆制动参数进行仿真实验，制动减速度为加了运行阻力的干轨条件下的紧急制动减速度，制动减速度精度为5 km/h一档。因为5 km/h速度分段最为细致，每一段的制动减速度最接近列车在各个速度下真实的制动减速度，所以以5 km/h速度分段计算得到的紧急制动降速曲线作为标准的紧急制动降速曲线。

当采用等间隔速度分段时，速度分段内采用平均减速度值，如果速度分段内减速度值波动较小，能较好反映列车在该速度分段内的真实减速度值，计算误差较小；如果速度分段内减速度值波动较大，就不能较好反映列车在该速度分段内的真实减速度值，计算误差较大。不同步长速度分段下，采用等间隔速度分段，列车从60 km/h制动停车所需制动距离如表2所示，不同速度分段个数的制动距离偏差走势如图4所示。在表2中，采用5 km/h等间隔速度分段，列车从60 km/h制动停车所需制动距离为103.23 m，采用30 km/h等间隔速度分段，列车从60 km/h制动停车所需制动距离为104.63 m，偏差为-1.40 m。

表2 不同步长速度分段的制动距离偏差比较(60 km/h)Table 2 Comparison of braking distance deviation of different step speed segments(60 km/h)

图4 不同速度分段个数的制动距离偏差走势图Fig.4 Brake distance deviation trend chart with different speed segments

如果采用等间隔速度分段，速度分段内的减速度值有时不能很好反映列车在该速度分段内的真实减速度值，所以按照列车制动减速度与速度的变化关系，对0～60 km/h范围进行2段不等间隔速度分段，列车从60 km/h制动停车所需制动距离如表3所示，不同速度分段点位置的制动距离偏差走势如图5所示。同样是对0～60 km/h范围进行2段速度分段，按表2中的等间隔速度分段，列车从60 km/h制动停车所需制动距离为104.63 m，偏差为1.4 m。如果以(速度，减速度)为坐标点绘制曲线，20 km/h处的曲率最大。从表3可见，对(0,60]速度范围，以曲率突变点20为分段点，采用(0,20)和(20,60)速度分段得到的计算结果精度接近最优。可见，根据列车制动减速度与速度的变化规律，以曲率突变点为分段点，采用不等间隔速度分段比采用等间隔速度分段计算得到的制动曲线要更为准确，可以提高制动曲线的计算精确度。

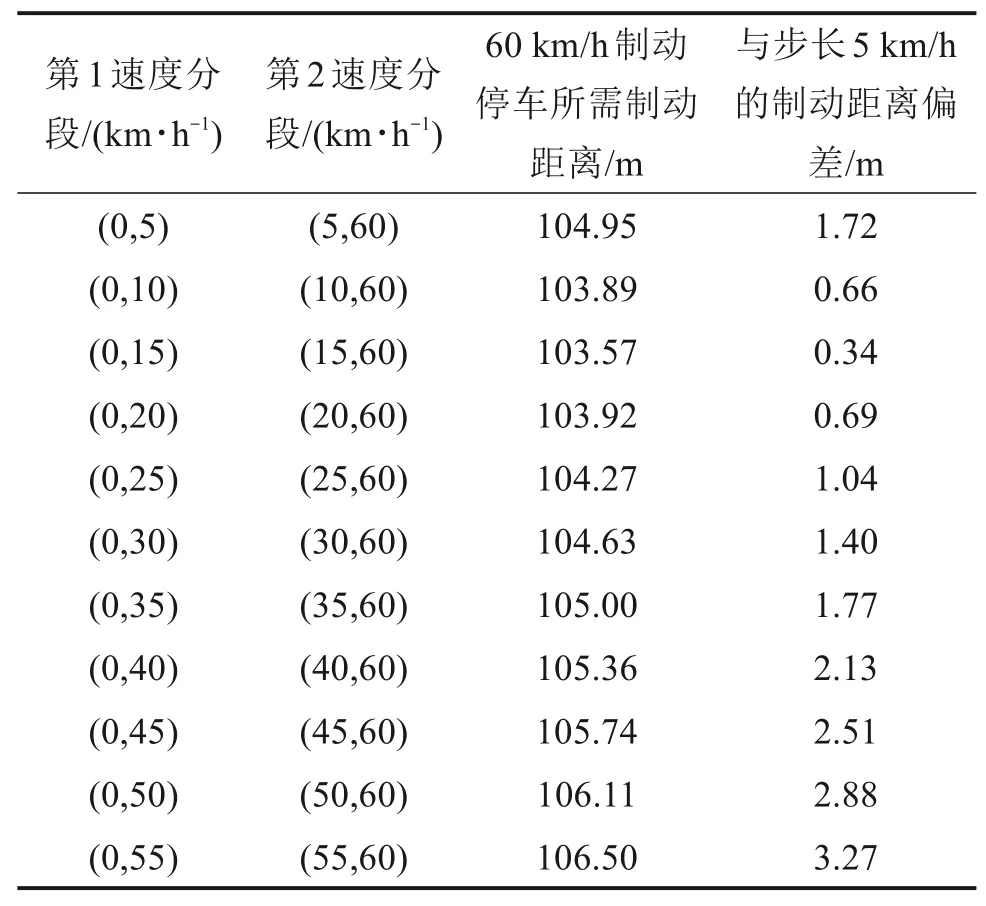
表3 不等间隔速度分段的制动距离偏差比较(60 km/h)Table 3 Comparison of braking distance deviation between unequal interval speed segments(60 km/h)

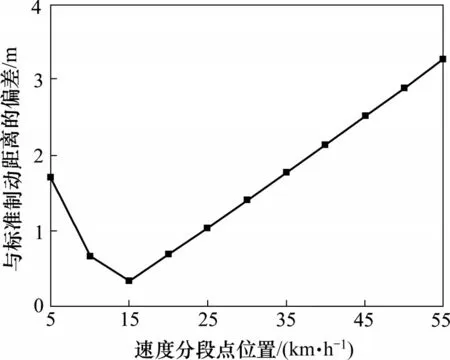
图5 不同速度分段点位置的制动距离偏差走势图Fig.5 Brake distance deviation trend chart at different speed segment points

4.3 速度分段个数对精度和效率的影响

分别按5，10，20，30，40，50，60，70和80 km/h对列车速度进行等间隔分段，每个分段内的制动减速度取平均值，使用图3的制动曲线计算模型推算列车从350 km/h制动停车的紧急制动降速曲线。不同步长的速度分段下，列车从350 km/h制动停车所需制动距离偏差走势如图6所示。通过对比和分析可见，速度分段个数越少，速度分段内取平均值的制动减速度与各个速度下真实的制动减速度偏差越大，计算得到的紧急制动降速曲线误差越大。因此，在车载设备计算能力允许条件下，在采用速度分段方式计算制动曲线时，应对速度进行更多分段，以提高制动曲线的精确度。但是，速度分段个数越多，计算量越大，降低计算效率。因此，应根据制动曲线精度要求，合理选择速度分段个数。

图3 高铁列车制动曲线计算模型Fig.3 Calculation model of braking curve of high-speed train

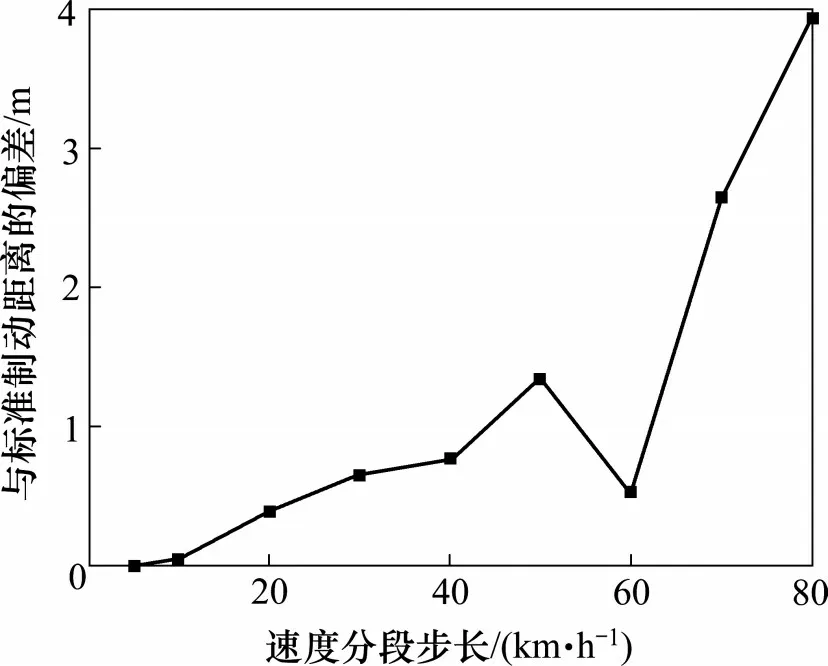
图6 不同速度分段步长的制动距离偏差走势图Fig.6 Brake distance deviation trend chart with different speed step sizes

4.4 分段内减速度选择对精度和效率的影响

图7 为速度分段内采用最小减速度和平均减速度，从350 km/h制动停车所需制动距离偏差比较。可见速度分段个数越少，制动距离越长，与标准制动距离(以5 km/h为速度分段步长，速度分段内采用平均减速度，从350 km/h制动停车所需制动距离)5635.12 m偏差越大。经过比较分析，与在速度分段内采用平均减速度相比，在速度分段内采用最小减速度，制动距离更长，降低运输效率。而速度分段内采用平均减速度，能保证制动距离计算结果的精确度，不会降低运输效率。

图7 速度分段内采用最小减速度和平均减速度的制动距离偏差比较Fig.7 Comparison of braking distance deviation using minimum deceleration and average deceleration in speed section

如果速度分段内采用最小减速度，速度分段个数足够多，也能保证制动距离精度的同时，不降低运输效率，例如选择速度分段步长为20 km/h或30 km/h。

4.5 速度分段方法

由4.3节可知，根据列车制动减速度与速度的变化规律，采用不等间隔速度分段比采用等间隔速度分段计算得到的制动曲线要更为准确，对以(速度，减速度)为坐标点构成的减速度曲线，以曲率突变点为分段点，可以将0 km/h到390 km/h分为(0,20]，(20,70]，(70,120]，(120,300]，(300,390]共5个速度分段。

对于速度分段(120,300]和(300,390]，虽然速度分段内的制动减速度曲率很小，但是速度分段跨度较大，平均减速度已不能准确反映整个速度分段内的减速度，计算出来的制动距离误差较大。根据4.4节可知，提高速度分段个数，可以提高制动曲线精确度。所以，可以在速度分段(120,300]内插入等间隔分段点210，在速度分段(300,390]内插入等间隔分段点345，将0 km/h到390 km/h分为(0,20]，(20,70]，(70,120]，(120,210]，(210,300]，(300,345]和(345,390]共7个速度分段，计算列车制动距离，如图8所示。从350 km/h制动停车，基本速度分段计算得到的制动距离为5 567.78 m，采用曲率和等间隔相结合的速度分段方法计算得到的制动距离为5 635.12 m，误差仅为67.4 m，不但误差小，而且制动距离变化曲线接近重合。

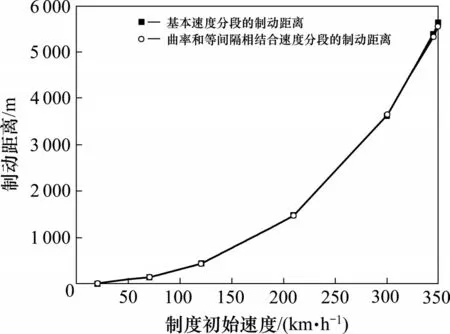
图8 曲率和等间隔相结合速度分段的制动距离偏差比较Fig.8 Comparison of braking distance deviation of speed segments combined with curvature and equal interval

经过仿真试验，根据列车制动减速度与速度的变化规律(例如，曲率突变点)进行一次分段，在一次分段的基础上，在跨度较大的一次速度分段内采用等间隔速度分段方法进行二次分段，采用最终的速度分段计算列车制动曲线，既能提高制动曲线的计算效率，也能保证制动曲线的计算精确度。

5 结论

1)根据列车制动减速度与速度的变化规律(例如曲率)进行分段，并提高速度分段个数，可以提高制动曲线的计算精确度；如果速度分段个数足够多，速度分段内采用最小减速度，也可以提高制动距离精度，不降低运输效率；如果速度分段个数较少，速度分段内采用最小减速度，制动距离较长，降低运输效率。

2)综合考虑车载设备计算制动距离精度的各个影响因素，提出曲率分段和等间隔分段相结合的速度分段方法。先采用制动减速度曲线曲率进行速度分段，得到一次速度分段；在跨度较大的一次速度分段内再进行等间隔速度分段，得到最终的二次速度分段，采用这种有限速度分段计算列车制动曲线，既能提高制动曲线的计算效率，也能保证制动曲线的计算精确度。此外，可根据计算精度要求，确定在跨度较大的一次速度分段内插入等间隔分段点的个数。

3)本文的研究成果可用于优化高速铁路列车列控车载设备制动曲线计算方法，提高制动曲线计算结果的精确度和计算效率，进而支持车载设备对高速铁路列车进行更为准确且实时的安全监控，保证列车行车安全，提高铁路运输效率。