基于双轴加速度的车辆坡度优化算法研究

彭邦煌， 刘梓曼， 刘倡廉

（比亚迪汽车工程研究院， 广东 深圳 518118）

坡度值可由车载产品以CAN报文的形式发出， 对于一些未带该配置的车型， 坡度值就需要根据其它信号进行计算， 但计算的坡度值在平路转弯、 换挡等工况时， 会出现大范围跳变现象。

坡度值的跳变会使其它需要用到坡度信号的产品策略失效， 导致非预期的结果。 例如遥控驾驶判断策略， 若在平路上使用遥控驾驶功能， 而由于坡度的跳变导致该功能未能成功判断处于平地， 从而进入不了遥控驾驶功能， 对用户的体验带来很大影响， 同时坡度值的显示跳变也会给驾驶员或乘客带来不佳的体验。

目前对于坡度值的计算方法主要有两种： 基于动力学模型的方法和基于运动学模型的方法。 文献[1]给出了一种基于动力学模型的坡度估算方法， 此种方法的坡度估计精度依赖于车辆模型， 而车辆模型中的各参数受高频噪声影响大。 文献[3]则基于运动学模型的方法， 通过利用加速度传感器进行坡度值的计算， 但文中只考虑了直线行驶工况下对坡度值的估算， 并未对转向、 换挡工况下坡度值计算进行研究。

为了解决车辆坡度在特定工况下跳变不准的问题， 本文拟提出一种优化后的坡度计算算法。 此算法基于运动学模型， 只需陀螺仪和车速信号， 通过引入横向、 纵向加速度以及挡位影响因素， 提升算法的准确性和稳定性， 从而提高坡度计算值的准确度和合理性。

1 经典坡度算法模型

1.1 基于运动学模型的坡度算法

基于运动学模型的坡度值算法是一种典型坡度算法模型， 其原理见图1。 该算法通过加速度传感器采集车辆运动过程中x方向 （汽车行驶方向） 的加速度， 结合整车车速信号， 利用运动学模型公式， 计算出对应坡度值。

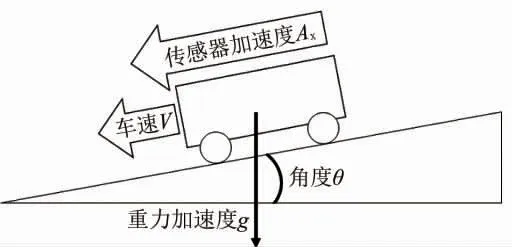
图1 算法原理图

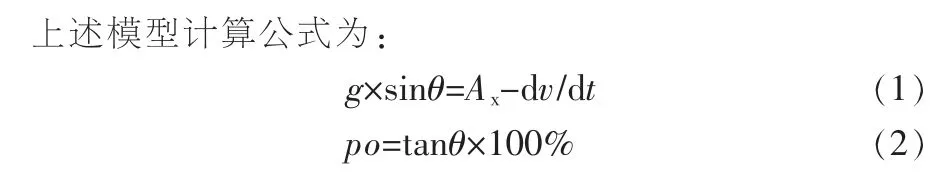
式中： θ——斜坡角度； A——传感器x轴 （车辆运动方向） 横向加速度； v——车速； dv/dt——车辆加速度；po——坡度。

1.2 基于动力学行驶方程的坡度算法

基于动力学行驶方程的坡度算法是将整车视作为一个刚体， 利用牛顿第二定律构建整车的动力学模型， 则汽车动力学方程为：

式中： F——汽车驱动力； F——滚动阻力； F——空气阻力； F——坡度阻力； F——加速阻力。

1.3 坡度算法模型的改进

基于动力学行驶方程的坡度算法在实际应用中， 多采用带遗忘因子的递归最小二乘法 （RLS） 来对坡度值进行估算， 如文献[4]。 此种方法需要对整车质量和坡度进行解耦， 运算量较大且不适用。

而基于运动学模型的坡度算法需要利用传感器加速度信息和整车CAN信号来进行坡度值计算。 在实际应用场景下， 外部操作导致整车CAN信号数值的跳变以及转弯工况下离心力导致传感器x， y方向加速度数据的偏差， 会导致坡度值异常跳变与数值不准。

针对上述问题， 本文在原有运动学模型算法的基础上，提出一种基于双轴加速度的坡度优化算法， 下文将详细阐述此算法的具体实现。

2 算法设计

2.1 数据滤波防振荡处理

本文涉及坡度计算的参数均由整车通过CAN信号给出，具体参数如表1所示。

表1 整车CAN信号参数表

坡度算法需要对数据进行滤波， 在本文算法设计中，选取500ms进行滤波处理。 结合上述参数CAN报文周期， 本文算法每25个信号进行一次滤波。

在本文算法实现中， 需要对传感器实际加速度和车辆加速度进行处理。

2.1.1 车辆加速度数据处理

由整车CAN报文获得的车速单位为km/h， 需要对车速量纲进行转化， 将第i个车速V（km/h） 转换成车速v（m/s），则有：

由于外界噪声的影响， 式 （4） 处理的整车车速v数值会有振荡 （见图2的车速滤波处理）， 数据需要进行滤波处理， 本文采用500ms均值滤波， 则滤波后的平均车速v为：

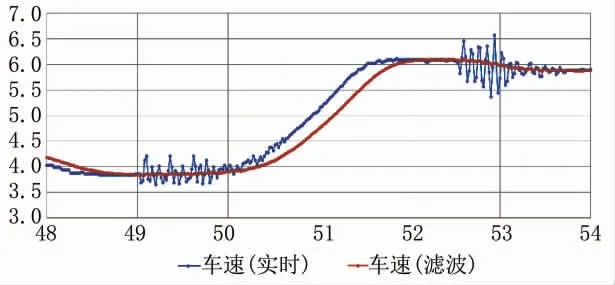
图2 车速滤波处理

针对式 （5） 处理后的车速， 采用车速微商转差商处理方法来获得车辆加速度， 令a=dv/dt， 则车辆加速度a为：

2.1.2 传感器实际加速度数据处理

考虑转向工况下对惯量传感器x轴与y轴方向加速度值的影响， 则实际加速度A、 A为：

图3 Ax滤波

2.2 基于双轴加速度的坡度模型建立

由于车辆转向工况 （图4）， 对车辆y向产生离心力作用。 式 （7） 为车辆相对x向数值， 而车辆在运动过程中有平动、 转动叠加效果， 所以需要综合考虑， 见图5。需要说明的是惯性传感器横向加速度A方向与车辆y 向为同一方向 （图4）。

图4 转向工况物理图

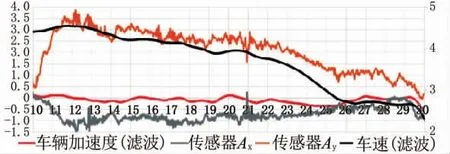
图5 转向工况滤波

惯量传感器物理模型见图6， 惯量传感器为二阶振荡模型， 如式 （11）。 由于车辆输入为低频周期力，惯量传感器振荡为高频周期， 满足指数衰减， 不对车辆低频周期力产生影响，故本文中不考虑系统固有振荡频率的影响。

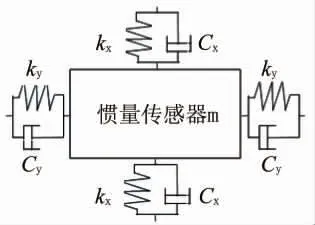
图6 惯量传感器物理模型

式 （15） 和式 （16） 为传感器x、y向位移与测量的加速度量值关系。

为计算方便， 本文认为k=k。 联立式（13）～式（16）， 则有：

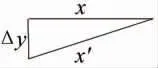
图7 惯量传感器微观分析

图8 Ax、 Ay滤波

将由式 （24） 计算得到的θ带入式 （2） 中计算即可得到坡度值， 由于坡度为稳态量， 需要进行滤波处理。 本文采用3s均值滤波， 在对滤波后的数值进行取整， 由公式（25） 和 （26） 即得到软件处理后最终坡度值。

3 算法验证

3.1 试验工况

在具体实施中， 本文选取某混动车型A和某燃油车型B进行实际拟合， 实车标定b=9.8， 分别在平路加减速、 换挡、 上坡、 下坡、 转弯工况下进行坡度算法验证。 其中车型A坡度值由网关产品计算出， 车型B坡度值由TCU产品计算出。

3.2 验证结果

3.2.1 小坡度工况拟合

算法坡度即本文处理后的坡度， 网关坡度为某产品测试坡度。 在小坡度工况下对车型A进行加减速和换挡操作，采集相应报文数据。 对该数据利用本文算法进行处理， 处理后如图9、 图10所示。

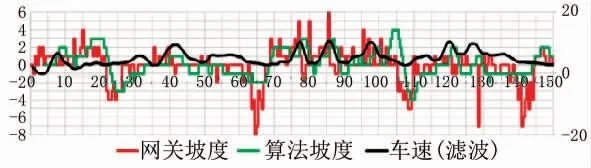
图9 小坡度加减速工况

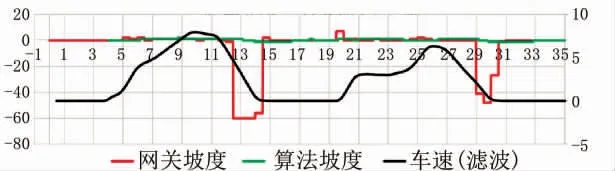
图10 小坡度换挡工况

从图中可以看出， 本文设计的算法能在一定程度上减少加减速工况下坡度值频繁跳变情况； 在换挡工况下， 能显著减少坡度值的异常跳变， 计算给出的坡度值更为准确。

3.2.2 上坡工况拟合

分别采集并记录车型A、 车型B上坡工况下报文数据，使用本文坡度算法处理后的数据如图11、 图12所示。 其中算法坡度即本文处理坡度， 网关、 TCU坡度为某产品测试坡度。

结合图11、 图12可知， 对比网关坡度， 本文算法能较好地抑制上坡工况下坡度值异常跳动， 算法计算出的坡度值曲线变化更连续， 更符合实际情况。 而相较于TCU坡度算法， 在上坡阶段， 本文计算给出的坡度值变化更均匀，且数值未出现异常跳变的情况。

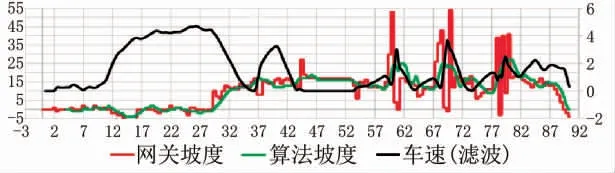
图11 车型A上坡工况

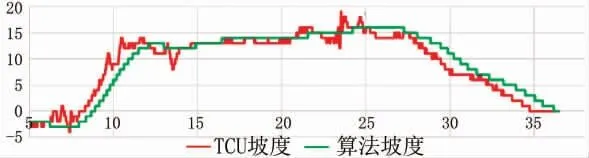
图12 车型B上坡工况

3.2.3 下坡工况拟合

分别采集并记录车型A、 车型B下坡工况下报文数据，使用本文坡度算法处理后的数据见图13、 图14。

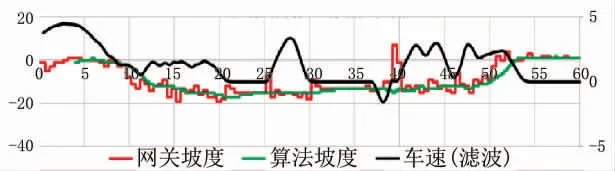
图13 车型A下坡工况

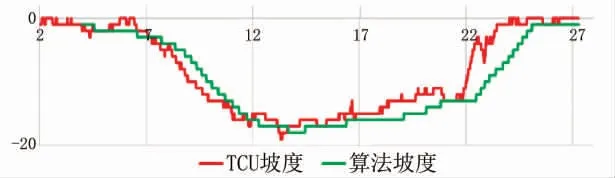
图14 车型B下坡工况

从图13和图14中能看出， 本文算法能很好地抑制下坡工况下坡度值的振荡， 能很好地抑制短时间尺度内坡度值异常跳变， 计算给出的坡度值更符合实际工况。

3.2.4 平路转向工况拟合

分别采集并记录车型A、 车型B平路转向工况下报文数据， 使用本文坡度算法处理后的数据见图15、 图16。

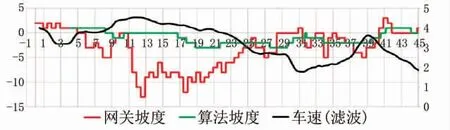
图15 车型A转弯工况

图16 车型A转弯工况

从图15和图16中能看出， 在平路转向工况下， 相比与其它两种算法， 本文算法计算出的坡度值更为准确和稳定，很好地抑制外部操作导致的坡度值跳变， 符合预期目标。

4 结论

本文坡度算法考虑了横向、 纵向加速度以及挡位的影响， 根据整车实际参数的CAN报文周期选取对应的数据段，对各个参数进行滤波、 修正， 得到最终的算法后选取两种车型进行算法拟合， 并对比现有产品的坡度算法验证本文算法的有效性。

通过以上工况验证， 本文设计车辆坡度算法， 在各工况下拟合效果明显， 能够有效解决车辆在加减速、 换挡、转向过程中坡度跳变导致坡度不稳的问题， 保证了坡度信号的准确性， 对其他涉及坡度信号条件判断、 坡度显示的产品提供了可靠性依据。