分数阶平流-扩散方程的隐式有限差分格式的稳定性分析

丁志清

(东莞理工学院城市学院，广东 东莞 523419)

分数阶导数的定义有几种：Grunwald-Letnikov(G-L)分数阶导数、Riemann-Liouville(R-L)分数阶导数、Caputo分数阶导数、Riesz分数阶导数以及Riesz-Feller(R-F)分数阶导数。分数阶微分方程包括分数阶常微分方程和分数阶偏微分方程。分数阶偏微分方程又分时间分数阶偏微分方程(时间导数是分数阶导数)，空间分数阶偏微分方程(空间导数是分数阶导数)以及空间时间分数阶偏微分方程(时间和空间导数均是分数阶导数)三大类。从实际问题背景中可以抽象出分数阶微分方程。Benson等人在讨论Levy运动时分别提出了分数阶Fokker-Planck方程和空间分数阶对流-扩散方程，通过与实验数据对比证实了用分数阶方程模拟Levy运动确实有很好的近似，并指出分数阶对流-扩散方程能更精确地模拟具有长尾性态的溶质运动过程。Chumer等人在研究多孔介质中溶质传输的Eulerian估计时，用分数阶Fick定律代替传统的Fick定律得到分数阶对流-扩散方程。

对于分数阶微分方程的解析解的求解主要有两种，一是积分变换及其逆变换方法，主要的积分变换方法有Laplace变换、Fourier变换和Mellin变换。二是分离变量法，其解析解的形式通常是用Green函数的卷积形式或用特殊函数的级数形式来表示。Liu等人考虑了时间分数阶对流-扩散方程，利用Mellin和Laplace变换得到了方程的基本解，其表达式是一个Fox函数，Huang和Liu考虑了空间-时间分数阶对流-扩散方程的解析解。

对于一般的分数阶微分方程，如变系数微分方程，无法求出其解析解，有些方程的解析解大都含有特殊函数，很难近似计算出来，故研究分数阶微分方程的数值解非常重要。近年来，反常扩散现象引起了人们的极大关注，广泛出现在等离子体、核磁共振、湍流、分形多孔介质、渗透媒介以及某些不纯介质中。正常扩散粒子的运动为布朗运动，本质上是一种马尔可夫局域性的运动，而对于反常扩散则是非马尔可夫非局域性的运动，为描述这种非局部扩散现象，需要用分数阶扩散(反应-扩散，对流-扩散)方程来代替整数阶扩散(反应-扩散，对流-扩散)方程。

本文考虑下列分数阶平流-扩散方程(FDAE)的初边值问题

(1)

u(x,t=0)=g(x)

(2)

u(0,t)=φ(t),u(Q,t)=φ(t)

(3)

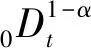
方程(1)描述了粒子的反常扩散现象，文献[1]中给出了方程的隐式有限差分格式

(4)

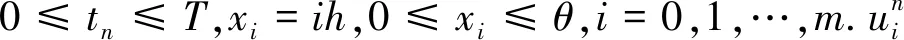
对隐式有限差分格式(4)，利用Fouier分析方法进行稳定性分析。

设时间步长τ和空间步长h比值满足一致有界性，令cn和un是差分方程(4)的两个解。

(5)

其中i=1,2,…,m-1,k=0,1,…,n-1.

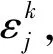
(6)

将εk(x)在x∈[0,Q]上展开成Fourier级数：

(7)

(8)

(9)

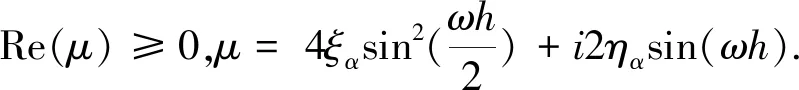
引理1 设ρk(k=1,…,n)是(9)的解，则存在常数M>0，使得|ρk|≤eM(k-1)τ|ρ0|。

证明：采用数学归纳法。

当ω=0时，则μ=0，结论显然成立。

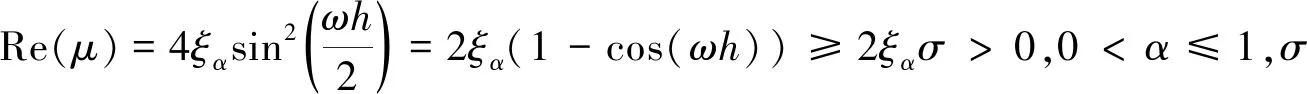
假设|ρj|≤eM(j-1)τ|ρ0|(j=1,2,…,k-1).则有

≤eMτeM(k-2)τ|ρ0|=eM(k-1)τ|ρ0|.

定理1 隐式有限差分方法(4)是无条件稳定的。

证明：由于(k-1)τ≤T,由引理1可得|ρk|≤eM(k-1)τ≤eMT|ρ0|≤K|ρ0|.

根据上式以及(8)式，得‖εk‖L2≤K‖ε0‖L2,k=1,2,…,n.即(6)式成立，从而隐式有限差分方法无条件稳定。