Nonlinear uncertainty quantification of the impact of geometric variability on compressor performance using an adjoint method

Qin ZHANG ,Shenren XU,b,* ,Xinjun YU ,Jixin LIU ,Dingxi WANG,b ,Xiuqun HUANG,b

a School of Power and Energy,Northwestern Polytechnical University,Xi’an 710072,China

b Key Laboratory of Aeroengine Internal Flows,Northwestern Polytechnical University,Xi’an 710129,China

c School of Energy and Power Engineering,Beihang University,Beijing 100083,China

d Research Institute of Aeroengine,Beihang University,Beijing 100083,China

Keywords Adjoint method;Aerodynamics;Compressor;Manufacturing;Monte Carlo method;Nonlinearity;Uncertainty quantification

Abstract Manufactured blades are inevitably different from their design intent,which leads to a deviation of the performance from the intended value.To quantify the associated performance uncertainty,many approaches have been developed.The traditional Monte Carlo method based on a Computational Fluid Dynamics solver(MC-CFD)for a three-dimensional compressor is prohibitively expensive.Existing alternatives to the MC-CFD,such as surrogate models and secondorder derivatives based on the adjoint method,can greatly reduce the computational cost.Nevertheless,they will encounter‘the curse of dimensionality’except for the linear model based on the adjoint gradient(called MC-adj-linear).However,the MC-adj-linear model neglects the nonlinearity of the performance function.In this work,an improved method is proposed to circumvent the lowaccuracy problem of the MC-adj-linear without incurring the high cost of other alternative models.The method is applied to the study of the aerodynamic performance of an annular transonic compressor cascade,subject to prescribed geometric variability with industrial relevance.It is found that the proposed method achieves a significant accuracy improvement over the MC-adj-linear with low computational cost,showing the great potential for fast uncertainty quantification.

1.Introduction

Manufactured compressor blades inevitably deviate from their intended shapes due to finite manufacturing precision.This usually leads to undesirable aerodynamic performance deterioration.Therefore,quantitative analysis of aerodynamic performance deviations is of great significance,especially for robust design and manufacturing tolerance tailoring.Theoretically,such Uncertainty Quantification(UQ) can be straightforwardly performed using the wellknown Monte Carlo (MC) methodbased on a Computational Fluid Dynamics (CFD) solver (denoted as MCCFD).However,a meaningful MC-CFD for threedimensional problems,requiring thousands of CFD calculations,is prohibitively expensive.Therefore,many models have been proposed to speed up MC-CFD,such as Polynomial Chaos(PC),surrogate modelsand so on.Nevertheless,the cost of constructing these models itself may increase exponentially with the dimension of the variables.Geometric deviation model reduction can be used to lower the cost,such as Principal Component Analysis (PAC) for the second-order sensitivity approach,but this comes with a reduced accuracy of the deviation representation depending on the particular application.

Linear models based on the adjoint gradientcan be used to efficiently perform UQ for high-dimensional problems.When scenarios arise where a linear approximation is inadequate to accurately represent the true functions,a quadratic modelbased on second-order derivatives can be constructed,but its computational cost again scales with the dimension of problems without a reduced accuracy of the deviation representation.In view of this,it is highly desired to have a method which can capture at least part of the nonlinearity between performance functional variations and geometric deviations while maintaining the low cost of the adjoint method based linear model.

In this work,a method is proposed to bridge the gap between the inaccurate linear model and the more accurate second-order quadratic model.It is applied to the UQ of a transonic compressor cascade subject to prescribed geometric deviation.The results show that the proposed method produces UQ results at low cost with satisfactory accuracy.The rest of the paper is organized as follows.Section 2 introduces the theoretical basics of the proposed method.Section 3 presents the UQ analysis results in detail.The conclusions are given in Section 4.

2.Adjoint method and uncertainty quantification models

2.1.Adjoint method

In this work,the objective function,J,representing mass flow rate,pressure ratio and efficiency,is expressed as

where W denotes the flow solution and α=[α，α，...，α]is the vector of geometric variables.W and α are implicitly related through the nonlinear residual,R(W，α),which always equals zero for a converged flow solution.With the adjoint method,the sensitivity is calculated as

where v is the adjoint variable and can be solved by the adjoint equation

Eq.(2)shows that dJ/dα can be obtained after only solving one flow and three adjoint equations(for three objective functionals in this study) regardless of the number of geometric variables.More details about the flow solver and the adjoint sensitivity verification of the adjoint solver can be seen in Refs.18,19.

2.2.Objective function perturbation due to a geometry change

From Eq.(2),the objective function change due to a geometry change can be obtained by the integral

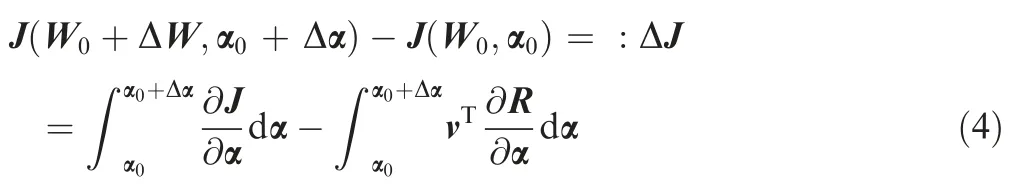
where,αis the original geometry and Wis the flow field solution of the original geometry.Note that the functional change calculated as above is exact,provided that the derivative in the integrand is accurate.Although this is theoretically valid,it is unpractical to evaluate the adjoint solution at each point from αto α+Δα.Subsequent subsections are concerned with obtaining the objective function changes with a low cost.

2.3.Monte Carlo method (MC-CFD)

Before discussing reduced-order approaches,the standard MC method is first discussed,serving as the reference method when evaluating alternative approaches.The idea and implementation of the MC method are rather simple.Once all deviated geometry samples are obtained,high-fidelity CFD solutions,and subsequently performance quantities,are obtained for all samples.Statistical information of the analysis results then can be computed as follows

where Jdenotes the aerodynamic performance of theth sample,is the number of samples,and E and σdenote the mean and variance of aerodynamic performance,respectively.

2.4.MC with linear models using adjoint gradient (MC-adjlinear)

Existing studies show that the performance changes almost linearly when the geometric deviations are small and the nonlinearity of the objective functions are weak.In consequence,∂J/∂α,vand ∂R/∂α can be assumed to be constant in the interval [α，α+Δα] and are all evaluated only at α.Therefore,the objective function perturbation is simply

This results in a linear model on which MC can be performed rapidly with negligible cost compared to a CFD calculation.The number of mesh perturbation is proportional to the number of geometric variables.The computational cost of the mesh perturbation is nearly negligible compared with calculating a nonlinear CFD solution.

2.5.MC with nonlinear models using adjoint method (MC-adjnonlinear)

The MC-adj-linear cannot capture the nonlinear effect due to the assumption that dJ/dαis constant.Only assuming that vis constant,but allowing ∂J/∂α and ∂R/∂α to vary in Eq.(4)yields

According to Newton-Leibniz Formula,Eq.(7) can be deduced as the model denoted as MC-adj-nonlinear

If assuming that ∂J/∂α,vand ∂R/∂α are constant in the interval [α，α+Δα],Eq.(7) is reduced to Eq.(6),which is identical to the MC-adj-linear model mentioned above.It can be inferred that when Δα is sufficiently small,Eq.(8) is expected to be more accurate than Eq.(6).However,it needs to be emphasized that the exact range of Δα in which the nonlinear approach outperforms the linear approach cannot be known a prior,as is the case for any reduced-order method.

The number of flow and adjoint solutions required by this method is the same as the MC-adj-linear.Different from MC-adj-linear,this method does not calculate sensitivities explicitly.Nevertheless,grid deformation is still required for calculating objective function perturbations for each sample.Therefore,the number of mesh perturbations required by this method is determined by the number of samples,rather than the number of geometric variables.When the number of samples is smaller than the number of geometric variables,MCadj-nonlinear is expected to outperform MC-adj-linear even in terms of computational cost.

3.UQ for an annular transonic compressor cascade

3.1.Test case

The test case used is an annular transonic compressor cascade.The airfoil is defined with the coordinates of 398 points.The inlet Mach number is 0.9.To perform UQ due to geometric variability,the geometric perturbations to the 398 points is prescribed,with a total of 2899 samples.The mean Eand the variance σof the geometric perturbations are derived from measurements of blades manufactured with the state-of-the-art manufacturing technology.The nominal blade,the average blade and the perturbed samples are compared in Fig.1.

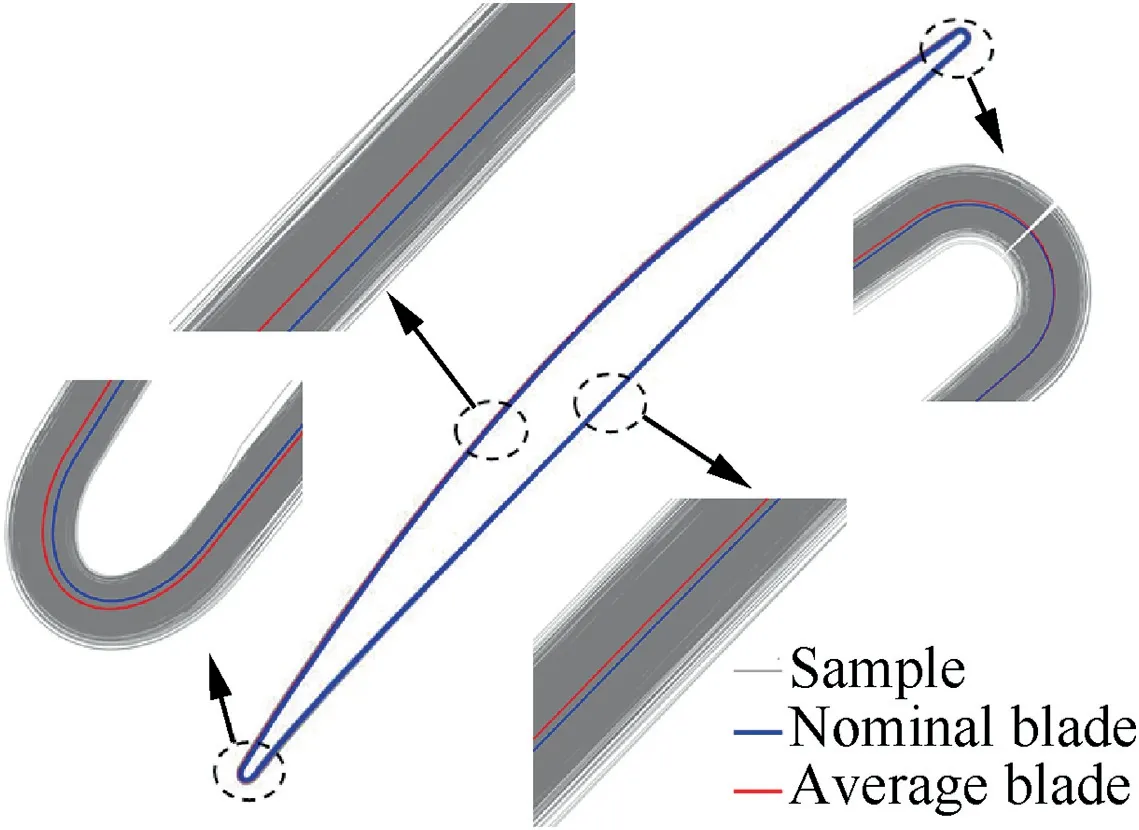
Fig.1 Nominal blade,average blade and samples.

3.2.LE/TE one-mode deviation

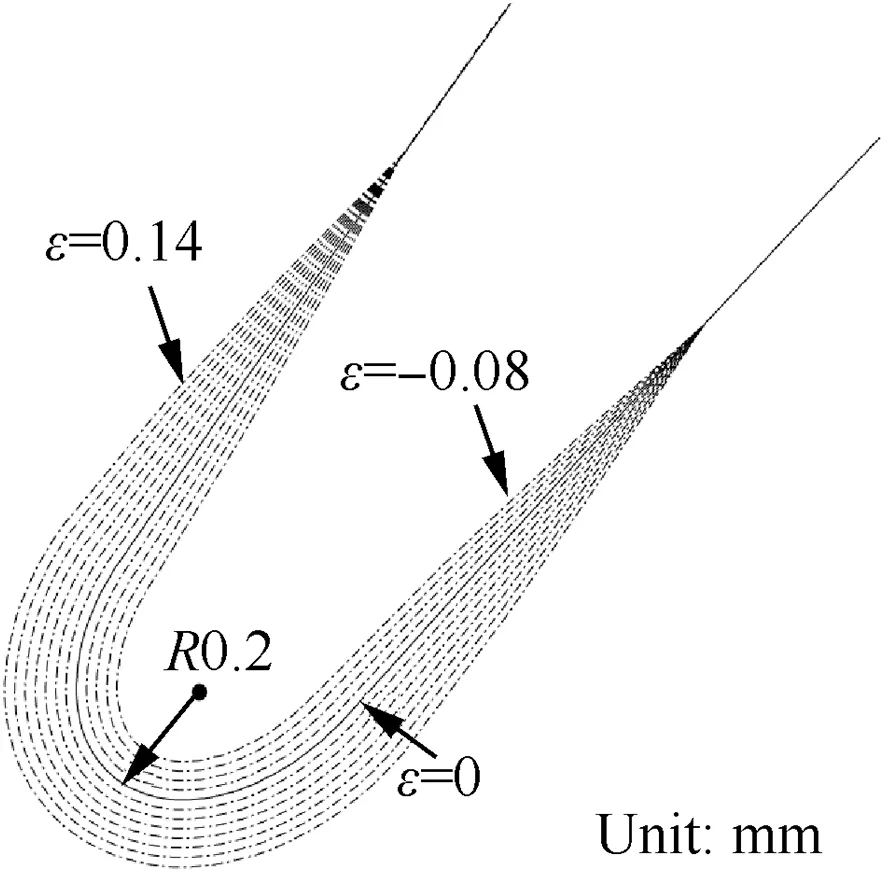
Fig.2 Geometric deviations in blade LE.

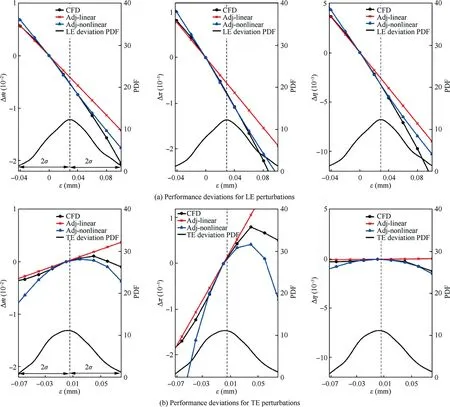
Fig.3 Objective functions with LE/ TE deviations with corresponding PDFs of deviations.

3.3.UQ of full profile deviation

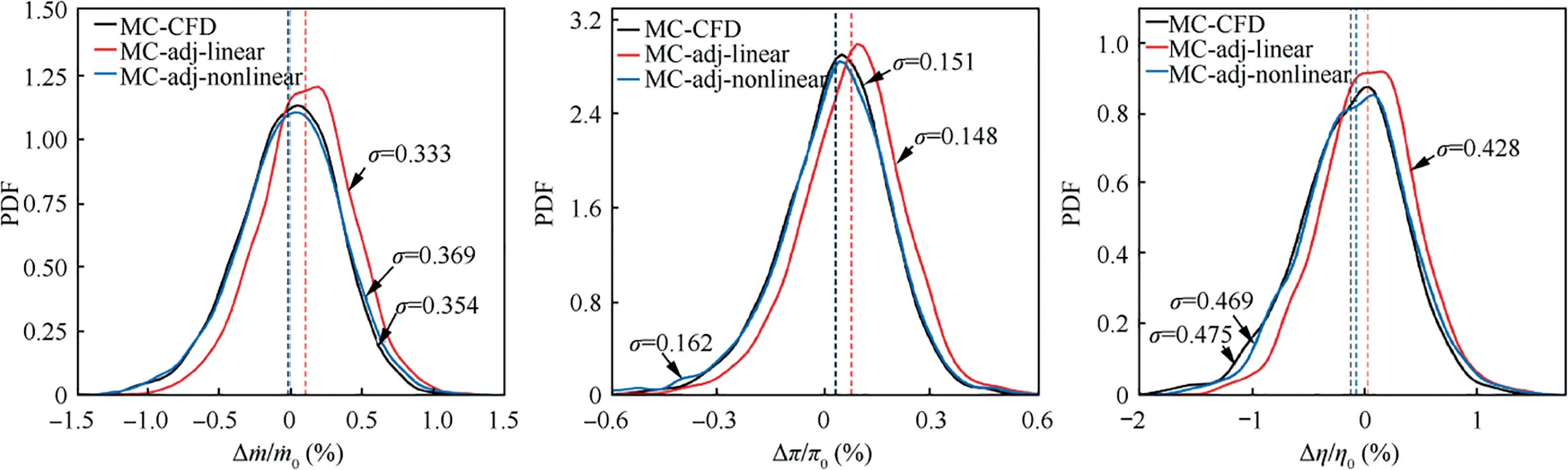
Fig.4 PDFs and statistics of aerodynamic performance deviations using three methods.

The time cost ratio of performing UQ for this case using the MC-CFD,the MC-adj-linear and the MC-adj-nonlinear is 67:1:7.The MC-adj-linear has the lowest time cost.The cost of the MC-adj-nonlinear is seven times of that of the MCadj-linear,which results from the number of samples being about seven times of the number of geometric variables.

4.Conclusions

(1) The proposed MC-adj-nonlinear can take the nonlinear effect into account,leading to a more accurate UQ compared to the MC-adj-linear.

(2) The time cost of the MC-adj-nonlinear is orders of magnitude lower than the MC-CFD method.

Future work will explore the efficacy of the method on three-dimensional turbomachinery components.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

The research is funded by the National Natural Science Foundation of China (No.52006177) fand National Science and Technology Major Project,China (No.2017-II-0009-0023).