Adjoint boundary sensitivity method to assess the effect of nonuniform boundary conditions

Xinrong SU,Xin YUAN

Key Laboratory for Thermal Science and Power Engineering of Ministry of Education,Tsinghua University,Beijing 100084,China

KEYWORDS Adjoint method;Coupling;Nonuniform boundary condition;Sensitivity;Turbomachinery

Abstract The performance of turbomachinery is largely affected by the nonuniform boundary conditions caused by the coupling between neighboring parts,such as the inlet distortion and hot streak.Existing works study this problem by comparing the flow fields with uniform and nonuniform boundary conditions,which is cost extensive.In this work a new and efficient method is developed by computing the sensitivities of arbitrary performance metric relative to the boundary conditions and this method quantitatively describes how the disturbance on the boundary surface affects the performance.The adjoint method popular in the design optimization is extended to current field for the efficient computation of the sensitivity.The extra cost is independent of the number of parameters describing the nonuniform distribution.Accuracy of the adjoint boundary sensitivity is validated against analytical results for a converging-diverging nozzle case.Its applications in a representative case are detailed and discussed in this paper.Current method provides a new tool,also direct guides to minimize the negative effect and improve the performance utilizing the adjoint boundary sensitivity.

1.Introduction

Gas turbine play an important role in both aerospace and power generation.Modern gas turbine is characterized by increasing aerodynamic and thermal loads.Every component in the gas turbine works in the complicated environment and its performance is heavily affected by neighboring components.For example,the fan is exposed to the inlet distortioncause by the inlet duct and the high-pressure turbine is affected by both hot streak and residual swirldue to the interaction between the combustor and the turbine.As a result,the flow on the interface separating neighboring components is nonuniform.Performance penalties will be created due to the non-uniform boundary conditions,for example,loss of stall margin cause by the inlet distortion and the risk of turbine blade ablation due to the hot streak.

Minimize the performance penalty caused by the nonuniform boundary conditions is a requisite for highperformance design.Besides,is it possible to improve the performance by sensibly exploiting the non-uniformity? These efforts require an efficient method to assess the effect of nonuniformity on the performance.In most existing studies about inlet distortion,hot streak and swirling flow,the effect of nonuniformity is assessed by comparing the baseline configuration of uniform boundary condition with the configuration of distorted boundary conditions.If the non-uniformity is described by several parameters,we have to conduct simulation or experiment for a series of configurations.The cost,or,equivalently,the number of simulations or experiments increases at least linear with the parameters describing the non-uniformity.Besides the cost issue,existing method is able to demonstrate the effect of the non-uniform boundary condition;however,it does not directly provide the sensitivity about how the non-uniformity quantitatively affect the performance.

Developing an efficient,quantitative and general method to assess the non-uniform boundary condition caused by coupling between neighboring components is the primary research interest of this work.Different from existing studies,in this work the effect of non-uniformity is transformed into the problem of sensitivity of arbitrary performance metric relative to the boundary conditions.The adjoint theory widely used in the design optimization communityis employed to compute the sensitivity.The cost roughly equals to an extra simulation and it is independent of the numbers describing the nonuniform boundary condition.The accuracy of current method is verified against analytical results.Its application for a typical case with hot streak is given and results faithfully explain existing observations about hot streak,also it provides quantitate proof on the possibility of performance improvement by exploiting the non-uniform temperature distribution.

2.Adjoint sensitivity about boundary condition

For a component in the turbomachinery,such as a blade,with the boundary conditiongiven,the flow field can be solved or measured.Then the performance metriccan be determined and expressed as=().Note thatcan be constant or spatially varying on the boundary.In the real engine,disturbance δto the boundary conditionis always caused by neighboring components,such as the wake of upstream blade,the potential field of downstream blade and the hot streak caused by the combustor.Also,the disturbance δmay come from active or passive control,such as the synthetic jets used to reduce flow separation.With the disturbed boundary condition+δ,the new performance metric is

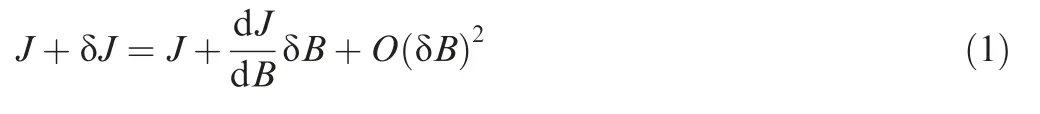
Eq.(1) is obtained by the Taylor expansion.Compared to the baseline configuration,when the disturbance from neighboring component is present,the change in the performance can be approximated by δ·d/d,by neglecting high-order terms.d/dis solely determined by the flow field of the baseline configuration.It means that after the component of interest is designed and the boundary condition in the baseline configuration is known,the sensitivity to any external disturbances can be determined.Furthermore,if δcaused by neighboring component is given,δcan be readily available,without resorting to the additional simulation nor experiment.Note that the second-order term in Eq.(1) can be recovered with the Hessian-based approach.The sensitivity d/dcan be obtained by perturbing the boundary conditionwith a small constant ε and then using finite difference in the form of

When the boundary conditionis constant along the surface,this method is quite efficient;however,for spatially varying,d/dis also spatially varying and we have to perturbon the boundary surface point-by-point and this is highly costdemanding.In this work the sensitivity d/dis calculated in an efficient fashion,inspired by the adjoint method widely used in the design optimization.The governing equation describing the flow inside the turbomachinery,such as the Navier-Stokes equation or the through-flow equation,can be generally expressed as R(U)=0 where U denotes the flow field.Ifis considered as variable,the flow-field is directly determined byand can be expressed as U=U().Differencing the governing equation and we can have

During the design process,also the analysis of the turbomachinery flow,one important concern is the sensitivity of the performance metric relative to the design variables.In the current work,if the effect of the boundary condition is to be considered,the sensitivity of performance metriccan be obtained with the following formulation:

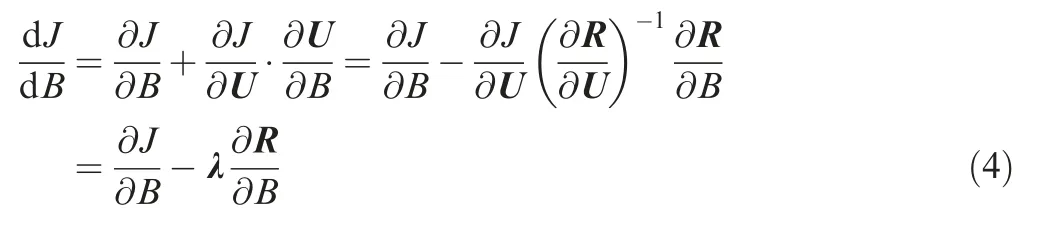
where λ is the adjoint variable and satisfies the adjoint equation λ·∂R/∂U=∂/∂U.In this work the adjoint equation is solved with a Krylov subspace method.In most cases,the performance metric is computed using the variables lying on the boundary,for example,the mass flow,the power output and the entropy rise.Let u denote the solutions on the boundary face and=(u).As a result,after solving the adjoint equation,the sensitivity of performance to the boundary conditions can be easily obtained as

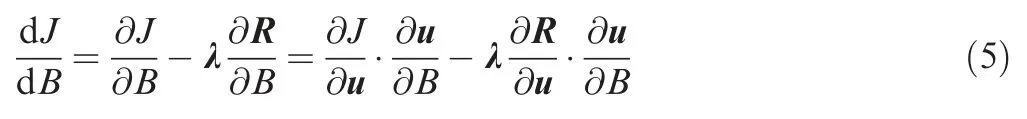
The above derivations do not rely on the detailed expression of the governing equation R(U),nor the numerical settings to solve the flow field U.Its applications in onedimensional,two-dimensional and three-dimensional problem,also with Euler and Navier-Stokes equations are validated by results in this paper.As a result,current method to compute d/dapplies with wide varieties of problems and can be regarded as a general theory.

3.Validation of accuracy of adjoint sensitivity

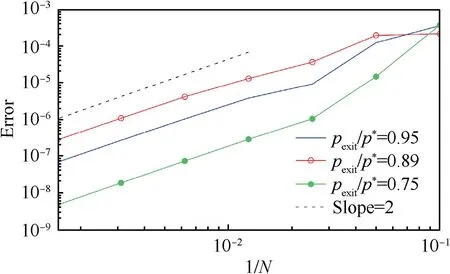
Fig.1 Convergence of error between numerical and analytical d/dp* with different mesh densities.

Fig.2 Convergence of error between numerical and analytical d/dT* with different mesh densities.

4.Adjoint sensitivity of turbine guide vane to hot streak

The inlet boundary conditions of turbine in real engine generally consists of temperature and velocity distributions varying in both radial and circumferential directions due to the interaction between the combustor and turbine.Reproducing enginerepresentative non-uniformities in the experiment remains a challenge.Most of the studies are conducted by comparing the numerical results from both uniform and non-uniform inlet boundary conditions with simulated temperature and velocity profiles.With the simulated boundary conditions,parameters including the amplitude,relative position and the nonuniform pattern can be changed to study their effects in a wide parameter space.In all the existing studies,a new simulation has to be conducted if the non-uniform inlet boundary condition is changed,which is cost extensive if many situations have to be considered.

With current method,this problem is simply transformed into computing the sensitivity.An engine-representative case about the inlet guide vane of high-pressure turbine is given here.After the flow field is obtained,the adjoint equation is solved and three performance metrics are interested,including the mass flow rate,entropy rise Δand the stagnation pressure loss coefficient ω.According to Section 2,the left-handsystems in the adjoint equation for different performance metric are the same and multiple adjoint variables can be obtained simultaneously by solving the adjoint equation only once.The cost is about 0.8 times of that elapsed in solving the Navier-Stokes equation.

First,a slice of the turbine cascade is simulated with twodimensional unstructured mesh.The adjoint boundary sensitivities are then computed.Typical results about Δalong the inlet are given in Fig.3(a) and (b) (denotes the pitch of the blade).Results indicate that Δis highly sensitive to the perturbations of inlet stagnation temperature and stagnation pressure for a small part on the inlet surface,which is related to the leading-edge region.The sensitivity of Δrelative to exit pressure along the outlet is negative,as shown in Fig.3(c),meaning that increasing the exit pressure will reduce the entropy rise.It is generally sinusoidal along the outlet surface.If non-uniform pressure perturbation to the outlet is possible,the best pitchwise position could be selected according to Fig.3(c) for minimal entropy rise.

Fig.3 Pitchwise distributions of dΔs/dT*,dΔs/dp* and dΔs/dpexit along outlet surface.

Then three-dimensional simulation with both blade and endwalls are simulated with multi-block structured meshdω/dis given in Fig.4 and note that the black line on the inlet surface denotes the contour dω/d=0.From Fig.4,dω/dpeaks in regions related to the leading edge and the endwall.For the circular region on the inlet surface which is related to the passage center,the sensitivity is also positive,while smaller than that related to the leading edge.In the literature,most studiesconcentrate on two special cases,the leading edge aligned and the passage center aligned hot streaks.The reasons can be quantitively explained with current method,as the adjoint boundary sensitivity peaks in both regions and the hot streak has prominent effect if entering the turbine from these positions.In the literature,circular hot streak is mostly assumed and it can also be explained with current method,as its effect will be distinct if the hot streak coincides with the position of circular distribution of dω/din Fig.4.

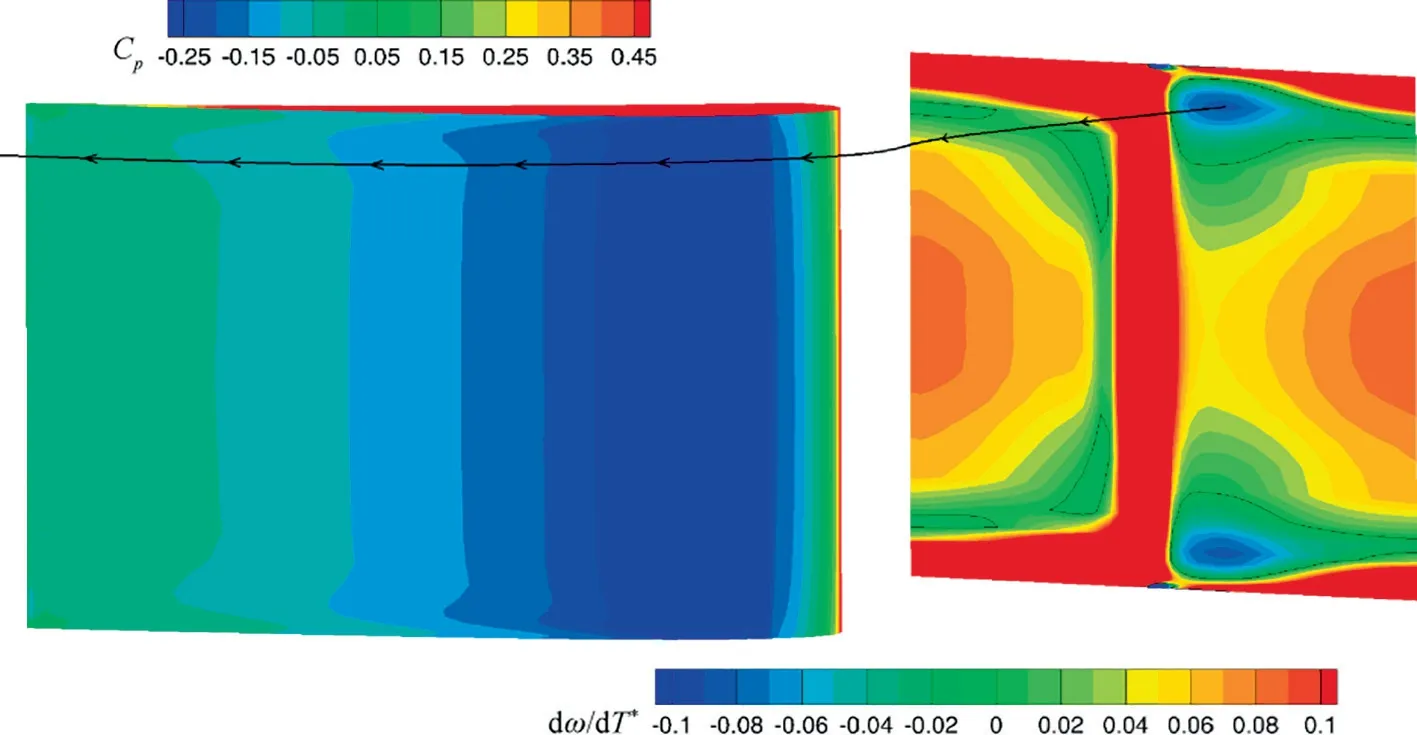
Fig.4 Distributions of dω/dT* on inlet surface together with pressure coefficient Cp on blade.

The sensitivity of ω with respect to inlet total pressureis given in Fig.5.According to Fig.5,dω/don the inlet surface varies mainly along the spanwise direction.In the midspan region,dω/dis negative except the region related to the leading edge.In the literature,Hermanson and Tholestudied the response of turbine vane to inlet total pressure deficit caused by the incoming boundary layer.The effect of nonuniformcan also be explained with current method.Fig.5 shows that between 5%～20% span,the sensitivity is positive in a triangular region and peaks near the region related to the pressure side.This region is closely related to the secondary flow and if the endwall region close to the pressure side has larger total pressure,the driving force for the secondary flow will also be stronger,thus enlarging the secondary flow loss.Close to the endwall dω/dis generally negative,with the exception that there is a small region where the sensitivity is positive and quite large.By plotting two streamlines as shown in Fig.5,these two regions are related to the pressure side leg and suction side leg of horseshoe vortex,respectively.The pressure side leg is linked to the region with negative sensitivity on the inlet surface and the adjoint boundary sensitivity suggests that the two legs of horseshoe vortex response differently to inlet disturbance.

Fig.5 Distributions of dω/dp* on inlet surface together with pressure coefficient Cp on blade.

For this case,the effect of the non-uniformity is computed with δ·d/dand compared with simulation results for typical hot streak.Results show that although current method is a linear approximation to the real effect,it provides accurate approximation,with the relative error smaller than 2%.If the non-uniformities caused by coupling cannot be avoided,the adjoint sensitivity provides direct guides to minimize performance penalty and maximize performance improvement.For example,gradient-based design optimization can be conducted to optimize the relative position between neighboring components.An interesting observation is the existence of regions where the sensitivities are negative in Fig.4,meaning that the hot streak there may reduce the aerodynamic loss.

5.Conclusions

This work proposes a new method to efficiently study of the non-uniform boundary conditions caused by the coupling between components.With current method,their effects on the performance are assessed by computing the sensitivities.The adjoint method widely explored in the optimization studies is extended to a new field in this work to compute the adjoint boundary sensitivity,with which the gradient of arbitrary performance metric relative to the boundary conditions can be computed at the extra cost comparable to only one cycle of simulation.Accuracy of the gradient is studied by comparison with analytical solution and second order convergence is confirmed.Applications of current method in a highpressure turbine are detailed and the adjoint boundary sensitivities quantitively explain existing observations about hot streak and also suggest potential mechanism for performance improvement.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

This work was supported by the National Natural Science Foundation of China (Nos.51876098 and 51911540475).Discussions with Dr.Juan Du of Chinese Academy of Science are deeply appreciated.