Pressure-induced instability and its coupled aeroelasticity of inflated pillow

Ji ZHANG ,Changguo WANG,* ,Jiaming GUO ,Jiawei ZHANG

a National Key Laboratory of Science and Technology on Advanced Composites in Special Environments,Harbin Institute of Technology,Harbin 150080,China

b Center for Composite Materials and Structures,Harbin Institute of Technology,Harbin 150001,China

KEYWORDS Aeroelastic analysis;Fluid-structural-thermal coupling analysis;Inflated pillow;Kink;Pressure-induced instability;Wrinkle

Abstract A floating air weapon system(such as airborne floating mines)plays an important role in modern air defense operations.This paper focuses on aeroelastic characteristics of airborne floating mine named inflated pillow.Firstly,the dynamic deployable process of the pillow and characteristics of the local instability of the edge are studied,and the evolution mechanism of wrinkles and kinks is analyzed.Secondly,in the cruising stage,the fluid-structural-thermal coupling analysis is performed on the pillow,and the aeroelastic characteristics are studied.Thirdly,the shapepreserving effect of the inflated pillow during the ‘‘negative pressure” slow landing stage is evaluated.It is found that when the wind velocity is higher,the pillow has a collapsed instability(surface extrusion and contact),and when the wind velocity is lower,snap-through instability occurs.Finally,for the collapsed instability,a carbon fiber skeleton is added to discrete the large global collapsed fold into small local folds,thus achieving shape-preserving effect of pillow.For snapthrough instability,the critical internal pressure and different shape evolution under different wind velocity are evaluated.Through the analysis of the mechanical mechanism and control of the structural morphological evolution,it provides theoretical guidance for the application of the curved shell structure in floating air weapon system.

1.Introduction

The construction of airborne weapons plays an important role in modern air defense operations.Especially for a region that does not have air superiority,according to the needs of air defense operations,building a floating air weapon system(such as airborne floating mines)may be used to prevent low-altitude and ultra-low-altitude attacks.Mylar balloons of different shapes and sizes have become popular as meteorological observation and communication.The most common balloons that are named inflated pillows in this paper are comprised of two circular sheets of mylar,fused together at the circumference.A small opening on the circumference allows the balloon to be inflated with either air or helium.These balloons are not spherical,which is at first surprising,for it is well known that the sphere gives the maximal volume for a given surface area.But as a simple aerostat structure,the pillow requires less gas to expand into a larger windward area than the sphere.It is flexible and has advantages in terms of aerodynamic drag during the cruising (2 km) and slow landing stage (2 km-0 m).However,there are few studieson the dynamic deployable process of the pillow,the local instability morphology,and the aeroelastic coupling characteristics under different morphological evolution.There are also not many documentssystematically expounding the ‘‘negative pressure” (the internal pressure of pillow is lower than the standard atmospheric pressure on the ground) global instability performance in the slow landing stage,the shape-preserving optimization designand the impact of the instability on aeroelastic performance.This article first studies the deployable process of pillow and the local instability characteristics of the edge.Then,the aeroelastic coupling characteristics of the pillow considering folds under different morphological evolutions are analyzed,and the aerodynamic drag is evaluated.Finally,the global instability of the pillow in the ‘‘negative pressure”slow landing stage is studied,and the large global fold of collapsed instability are discretized into multiple small local folds to achieve shape-preserving,and the critical load of the snapthrough instability is analysed.

2.Local instability from wrinkles to kinks

The pressure for the pillow includes positive pressure (inflated pressure)and negative pressure(wind pressure).There are two types of instability corresponding to two pressure cases.The instability caused by positive pressure is local instability,including wrinkles and kinks at the edge of inflated pillow in the cruising stage.The instability caused by negative pressure is global instability,including snap-through instability under smaller wind pressure and collapsed instability (surface extrusion and contact) under larger wind pressure.

The characteristics of local instability during the deployable process are analyzed.The results of deployable process are displayed in Fig.1(a),and the diameter of the deflated pillow is 424 mm.Abaqus is used to simulate its volume and internal pressure changes when the inflation pressure is 20 kPa.It is found that after the internal pressure is greater than 1.5 kPa,the volume of inflated pillow basically no longer increases,and it can be approximately considered that it has been fully expanded.At this time,the height of the pillow has also been given,and the calculated results are in good agreement with experiment.

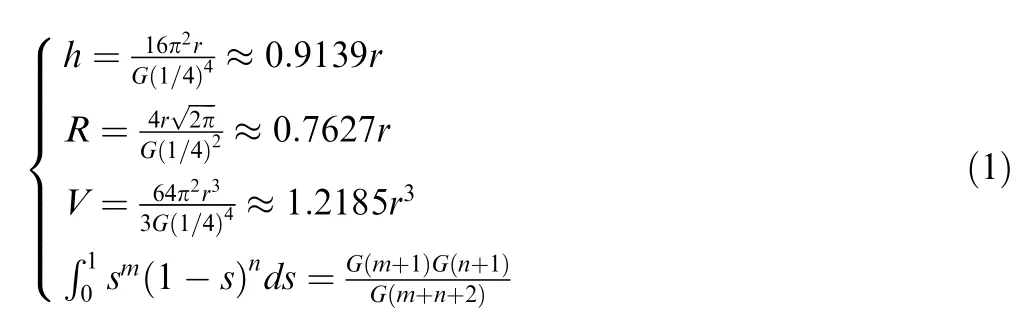
The height,radius,volumeof the inflated pillow and the general form of the Beta integralis given by:whereis the radius of the deflated pillow;is the general form of the Beta integral;andare constant,=-3/4，=1/2;is integral variable.

The height,radius and volume of the inflated pillow calculated by Eq.(1) are 193.75 mm,161.69 mm,11.61×10mmrespectively,and the calculated results by Finite Element Method (FEM) are in good agreement with the theories.

During the deployable process,the edge of pillow gradually becomes unstable(Fig.1(b)).When the internal pressure is relatively larger(1.5 kPa-20 kPa),the inside of the pillow is under tension without wrinkles.At its edge,a mixture of wrinkles and kinks appear and this is a form of local instability.

The amplitude of the wrinkles and kinks in the circumferential direction under the pressure of 2 kPa is shown in Fig.1(c).The outer ring on the right side of the figure shows the shape of the deflated edge.As the pressure increases,the edge gradually shrinks inward.When the internal pressure is small,all are wrinkles.As the internal pressure increases,a state where wrinkles and kinks are mixed appears.If the edge is discretized into many nodes,when the node displacement along the radius is relatively small (＜45 mm),the localized converse folding area is wrinkle area,and when the displacement is relatively large(＞45 mm),it is kink area.

The local instability around the inflated pillow during and after deployment are difficult to evaluate from a theoretical perspective.We found that before inflating,the local area produced by wrinkles or kinks is approximately straight,and as the inflation continues,the area continues to bend.The axial length,curvature and cross-sectional radius of the local area where the inflated pillow produces wrinkles or kinks are equivalent to the inflated beam,and then qualitatively evaluated the instability mode.The critical bending moment when wrinkles and kinks appear are simply evaluated.

The Brazier modelis used to describe the critical wrinkling stress σ:

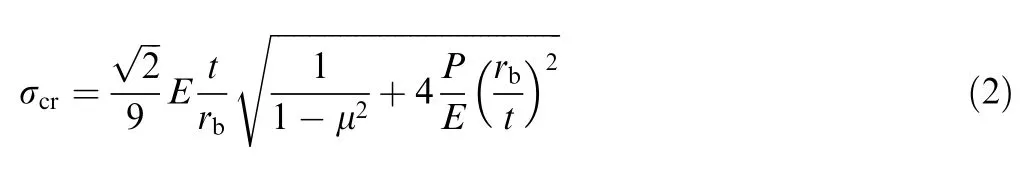
whereis modulus of elasticity;is thickness;is crosssectional radius of beam;μ is Poisson’s ratio;is inflated pressure.

The continuum moment equilibrium at any point on the beam surface gives the critical wrinkling moment,and it can be expressed as:

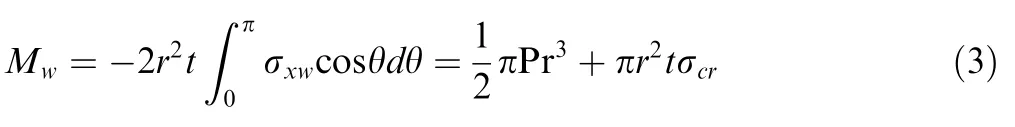
where σis axial wrinkling stress;θ is wrinkling angle.

Integrating the stress distribution by combining the axial stress and the cross-sectional stress gives critical kinking moment,and it can be expressed as:

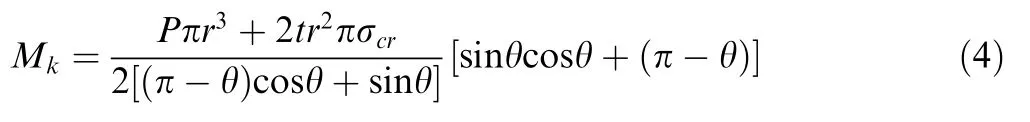
As shown in Fig.1(d),it is found that in the wrinkling stage,as the cross-sectional radius increases,the critical bending moment gradually increases;in the kinking stage,as the crosssectional wrinkling angle increases,the bending moment also increases.This shows that with the appearance of kink and the evolution of shape,bending load is getting bigger and bigger.

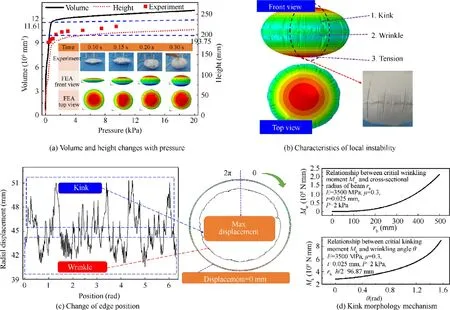
Fig.1 Dynamic deployable process of pillow.

3.Fluid-structural-thermal coupling analysis of inflated pillow considering folds

For thermal-structural coupling analysis,it is mainly used when force field and temperature field exist at the same time,and the mutual influence is very large,that is,stress analysis is based on temperature distribution,and temperature distribution is based on stress solution.The thermal-structural coupling algorithm in Abaqus/Explicit uses explicit forward difference time integration rule to integrate the heat transfer equation into the mechanical solution of explicit centraldifference integration rule,then:

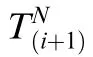
Based on the pre-and post-processing of Abaqus/CAE(Computer Aided Engineering),the increasingly mature Abaqus/CFD has the capability of Computational Fluid Dynamics(CFD),which can solve incompressible fluid-thermal,fluidstructural and other problems with the following characteristics:laminar or turbulent,steady or transient state,internal or external flows,thermal convective,deforming-mesh.

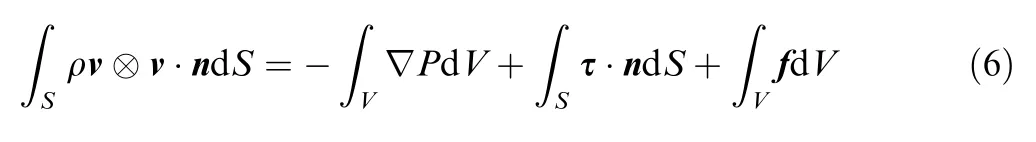
The steady momentum conservation equation for any control volume can be expressed as:where ρ is the fluid density;V is the velocity vector;n is the outer normal of the surface;is surface area;τ is the viscous shear stress;f is the volume force.

The temperature transfer for energy conservation can be expressed as:

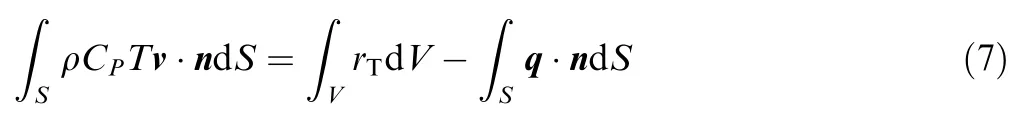
where Cis the specific heat under pressure;is the temperature;is the external heating per unit volume;q is the heat flux density.

The temperature of a certain day in early autumn in northeastern China at an altitude of 2 km is selected as the external environment when the inflated pillow is in the cruising stage,and the temperature curve with time is like a mountain peak from 0 to 24 hours.The highest temperature in a day is about 14.5 h,and the lowest temperature is about 4.5 h.

It is found that after the pressure is stabilized,the pillow is soft when the pressure is at 0 Pa-0.5 kPa.As the internal pressure increases,the stiffness gradually increases.Changes of stress and pressure with time at different temperatures is performed,and the results are shown in Fig.2(a).At 2 kPa,the stiffness is large,and the internal pressure at this time is used as the initial condition for the study.When the gas in pillow is constant,the internal pressure will increase as the temperature increases.The pressure at different times and the maximum stress in the middle of the pillow are calculated,and it is found that the maximum stress occurs at the highest temperature.The tensile fracture stress of the Polyimide film (thickness of 25μ) is 83.77 MPa,which is used as a criterion for judging whether the film fails.But affected by temperature,the stress change is only 0.6 MPa,which is far below the strength limit of the material.

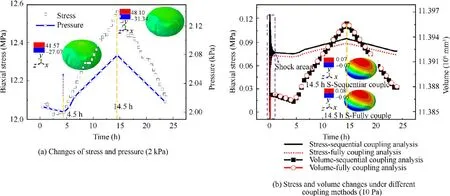
Fig.2 Influence of temperature on inflated pillow.

As shown in Fig.2(b),the sequential thermal-structural coupling and fully thermal-structural coupling analysis of pillow found that the results of the two calculations are basically consistent,but at the beginning,the sequential thermalstructural coupling will produce a shock area,and then immediately stabilize.When performing fluid-structural-thermal coupling analysis,if Abaqus adopts fully coupling between structural and heat,it will be more difficult to converge.Therefore,the sequential coupling is adopted,and then the calculation with the fluid adopts co-coupling analysis.

The stress analysis of an ellipsoidal shell under internal pressure is carried out,and the stress equation is:

where，are the long and short radius of the ellipsoid shell respectively;is the distance between any point and the central axis of the ellipsoid shell;σ,σare the,direction stress of point on ellipsoid.

Under internal pressure of 10 Pa,calculated from Eq.(8),the biaxial stress at the upper center of the inflated pillow is 0.069 MPa,and under internal pressure of 2 kPa,the calculated biaxial stress is 13.89 MPa,which verifies the accuracy of FEM.

Since the pillow has the largest stress at highest temperature,the fluid-structural-thermal coupling analysis is only performed at the highest temperature.In this paper,multi-physics coupling calculations are used.Firstly,the transient thermal temperature field of the pillow is analyzed,and then the result of transient thermal calculation is applied as a boundary condition to the inflated pillow for sequential thermal-structural coupling analysis;At the same time,the wind pressure is used as the boundary condition of the flow field to establish the flow field model;Finally,fluid-structure-co-simulation boundary between the outer boundary of the pillow and the contact area of the flow field are established to realize a coordinated indirect fluid-structural-thermal coupling analysis and exchange data.

A three-dimensional model of the flow field is established,and the direction of the wind is blowing from left to right.In the left plane of computational domain (cuboid),the velocity inlet is adopted.The setting condition of the right plane is the pressure outlet.The surface of pillow is set to non-slip wall constraints (Wall:no slip),and the walls around the calculation domain are set to slip constraints (Wall:specified shear,symmetry).

The analysis of drift distance of different morphological(horizontal and vertical) pillows shows that at a wind velocity of 2.77 m/s(altitude is 0 km,time is 0.1 s),the drift distance of the horizontal pillow is 69.30 mm,and the drift distance of the vertical pillow is 79.99 mm.At a wind velocity of 8.50 m/s(altitude is 2 km,time is 0.1 s),the drift distance of the horizontal pillow is 264.76 mm,and the drift distance of the vertical pillow is 401.00 mm.As shown in Fig.3,the drag force of horizontal and vertical pillow at different wind velocity is analyzed,and it is found that when the wind velocity is 8.5 m/s,the drag force of the vertical pillow reaches 1.264 N,of which the viscous force is 0.028 N,and the differential pressure is 1.236 N.The total force of the horizontal pillow is 0.265 N,of which the viscous force is 0.026 N and the differential pressure is 0.239 N.The drag force of the vertical pillow is about 4.77 times that of the horizontal pillow.Under the same wind velocity,the drag force of the vertical pillow is greater and the drift distance is longer.

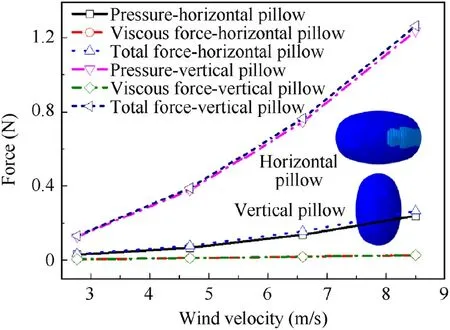
Fig.3 Aerodynamic force of inflated pillow.

4.Global instability under ‘‘Negative pressure’’ and shapepreserving effect

On the ground,the atmospheric pressure is 1.013×10Pa and the air density is 1.225 kg/m.At an altitude of 2 km,the atmospheric pressure is 7.950×10Pa,the air density is 1.007 kg/m,and we set internal pressure of pillow to 0 Pa at this altitude.According to ideal gas law,it can be seen that the internal pressure of the pillow on the ground is about 20 k Pa.This part mainly conducts the f luid-structural-thermal coupling analysis of pillow under the slow landing stage.

Theinternalpressureand volumechangeswithaltitudeduring the slow landing stage are calculated in Fig.4(a),and the internal pressure is 0 Pa at an altitude of 2 km.During the descent,as the altitude decreases,the external pressure gradually increases.The pillow is squeezed,causing the internal pressure to increase and thevolumetodecrease.Accordingtotheidealgasstateequation,it is calculated that the volume is reduced by about 1/5,which is consistent with the simulation result.

As shown in Fig.4(b),under ‘‘negative pressure” conditions,when the wind velocity is high(8.50 m/s),the pillow will collapse (squeeze/contact) and become fail (collapsed instability);when the wind velocity is low (2.77 m/s),the pillow will experience snap-through instability.The local and global folds have a great inf luence on the f low f ield.

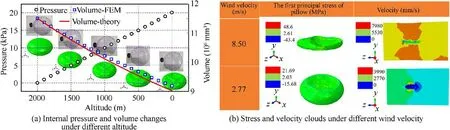
Fig.4 Mechanical and morphological evolution characteristics in slow landing stage.

In view of the seriousness of the above problems,many effective measures should be taken before things get worse.Strategy A is to add a carbon f iber skeleton inside or outside the pillow,so that the upper and lower surfaces are no longer dangerous under‘‘negative pressure”.Strategy B is to evaluate the morphological evolution of the pillow through the instability of the ellipsoidal shell.By evaluating the collapsed degree of the pillow under different wind pressure to judge whether it is invalid.

4.1.Strategy A-the role of carbon f iber skeleton

As shown in Fig.5,a carbon f iber skeleton is added to the pillow to study the shape-preserving effect in the slow landing process.The radius of the carbon f iber tube is 1.5 mm,the thickness is 0.3 mm,the elastic modulus is 84 GPa,the Poisson’s ratio is 0.3,and the density is 1405.7 kg/m.After adding the carbon f iber skeleton,it is found that even if the internal pressure in the initial state was 0 Pa(2 km),it could still maintain a good shape during the slow landing process.

Fig.5 Structural optimization during slow landing process.

The role of the skeleton can be summarized as follows:(A)It has a good shape-preserving effect at the ‘‘Negative pressure” slow landing stage;(B) The large global collapsed fold discrete is divided into many small local folds;(C) Based on demand,add carbon f iber to any position so that it can be recessed in different parts;(D)The distribution of velocity f ield and f low f ield can also be re-divided into what we want.

4.2.Strategy B-evaluation of snap-through instability and shape optimization

Firstly,the snap-through instability of shells with different apex rises (for the theoretical part,please refer to Ref.) is studied.As shown in Figs.6(a)and(b),we found that when the apex rise (2 mm) is relatively small,there is no negative stiffness effect.When the apex rise (4 mm,6 mm,8 mm) is greater or equal to 4 mm,a snap-through instability occurs.When apex rise is greater than 8 mm,the error is already large,so the theory cannot be used to calculate the snap-through instability of the f lat thin ellipsoidal shell with a large apex rise and we adopt FEM.As the apex rise increases,its critical instability load also gradually increases.

The relationship between def lectionof center point and loadis:

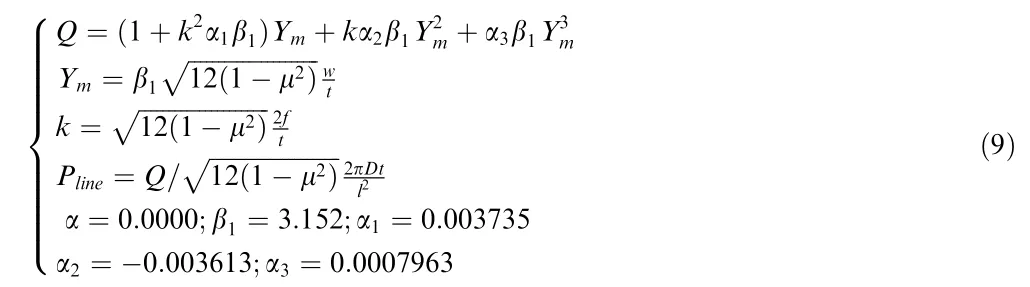
whereis a parameter indicating whether the shell is buckled;β,α,αand αare coeff icient and their values are shown in Eq.(9)is a parameter related to def lectionof the center point;is bending stiffness;is half of the span of f lat thin spherical shell;is the apex rise;is the uniform linear load;α=0.0000,which means concentrated load.

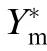
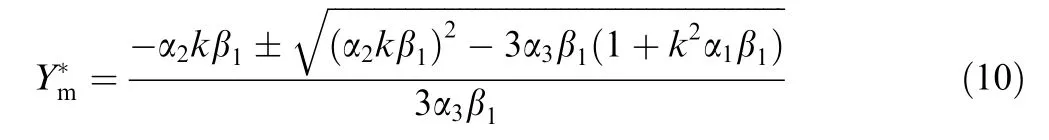
The wind pressure at different wind velocity and the critical internal pressure of snap-through instability are shown in Fig.6(c),and the relationship between wind pressure Pair and wind velocityis=1/2ρ(ρis the air density).It is found that when the displacement of the center point is 48.43 mm,there is a critical status of snap-through instability of pillow.For instance,when internal pressure of pillow is 1 Pa,the wind speed of 6.3 m/s can make the pillow snapthrough.Through the critical pressure difference of instability at different wind velocity and the degree of instability can be used to judge the snap-through instability of pillow,and then determine whether the pillow is out of work.

Based on the inspiration of the bistable shell and the accuracy of FEM,we designed a bistable pillow that is easy to be inflated and deployed,as shown in Fig.6(d)(Volume is volume change of pillow we studied above,and Volume-snap-through instability and Volume-hyperelasticity is volume change of bistable pillow).The deployment of the bistable pillow under different internal pressures is studied,and it is found that the bistable pillow can be fully expanded under a smaller pressure.Rubber materials’s bistable pillow can also be quickly inflated and have a greater rate of volume change due to lower stiffness,and it is beneficial to have good aeroelastic performance at the moment of inflation.

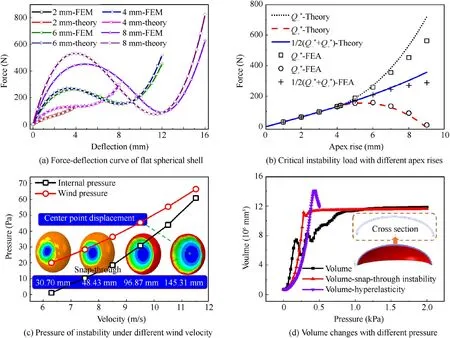
Fig.6 Snap-through instability and shape optimization of pillow.

5.Conclusions

This paper mainly studies pressure-induced instability and conducts the fluid-structural-thermal coupling analysis of inflated pillow under the cruising and‘‘negative pressure”slow landing stage.For local instability,wrinkles and kinks characteristics at its edge during deployment process are analyzed.In view of the collapsed and snap-through instability (global instability) under higher wind velocity,carbon fiber skeleton,critical snap-through internal pressure,bistable pillow are added for optimization design.

Firstly,the pillow is dynamically deployed,and when the internal pressure is relatively larger,the inside of the pillow is under tension without wrinkles.As the pressure increases,there is a mixed state of wrinkles and kinks at its edge.Secondly,in the cruising stage,it is found that under the same wind velocity,the vertical pillow drifts farther and suffers greater drag forces.Thirdly,in the slow landing stage,it was found that the external pressure gradually increased and the pillow is squeezed,resulting in an increase in the internal pressure and a decrease in volume.The pillow cannot withstand higher wind velocity under internal pressure of 0 Pa.Therefore,the structure optimization design of the pillow is carried out,and the carbon fiber skeleton is added,which can effectively control the recessed part,and improve the stiffness of structure.Finally,for snap-through instability of pillow,the critical internal pressure and different shape evolution under different wind velocity are evaluated.A kind of bistable pillow is designed,and it is good for aeroelastic performance at the moment of inflation.We wish the results obtained in this paper are good references for the design of floating air weapon system.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

The authors gratefully acknowledge the financial support from the National Natural Science Foundation of China(11872160),and the Science Foundation of National Key Laboratory of Science and Technology on Advanced Composites in Special Environments,China (JCKYS2020603C007).