Transit time difference and equal or non-equal transit time theory for airfoils with lift

Chenyun BAI ,Ziniu WU

a Ministry of Education Key Laboratory of Fluid Mechanics,Beihang University,Beijing 100083,China

b Department of Engineering Mechanics,Tsinghua University,Beijing 100084,China

KeywordsAirfoil;Equal transit time theory;Lift;Non-equal transit time theory;Transit time

Abstract The transit time difference of fluid particles moving along the upper and lower surfaces of a lift-producing airfoil is studied here both theoretically and numerically.We show that,under thin airfoil assumption and for potential flow,the transit time difference is equal to the circulation divided by the square of the inflow velocity and the lift coefficient is equal to half of the number of chords travelled by the airfoil during the transit time difference.An analysis of transit time difference for very thick airfoil(c.f.very large angle of attack)suggests the transit time may change sign beyond thin airfoil assumption,a conclusion supported by an example of flow with an attached vortex.Thus,fluid particles may transit the upper surface with less,equal and more time than those transiting the lower surface for lift producing airfoils,depending on the configuration of flow structure and geometry.

1.Problem statement

Though scientists and engineers know perfectly how to design wing to produce adequate amount of lift,the most fundamental reason for this lift production receives interests in educational and science communication societies.Among the various reasons proposed (c.f.Newton’s third law of motion,codependency of lift’s four elements,the creation of a vacuum,the equal transit time theory),the equal transit time theory (which is also known as the long path theory and which assumes fluid particles take equal time to transit the upper surface than the lower surface) enjoys wide belief (c.f.in aircrew training manuals and in school textbooks,as pointed out by Ackroyd),though it was shown (at least for the cases considered) to be wrong.

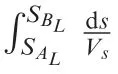
Fig.1 Schematical display of fluid particle path.

In this work we will study the transit time difference=t-tby relating it to the lift coefficient Cor circulation Γ (positive if anticlockwise),first under strict invicid potential flow assumption and then discuss the meaning of the result in two practical flow conditions beyond potential flow assumption.For＜0 s，=0 sand＞0 s,fluid particles take less,equal and more time to transit the upper surface than the lower surface.

2.Statement of results

Using complex variables the transit time difference can be expressed as

where Cis the contour of the airfoil directed in the anticlockwise direction,d=d+d,and υ=+is the conjugate of complex velocity.The complex velocity is related to the complex potential()=φ+ψ (φ is the potential function and ψ is the stream function) by

and the lift coefficient is given by half of the number of chord travelled during the transit time difference,i.e.

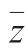
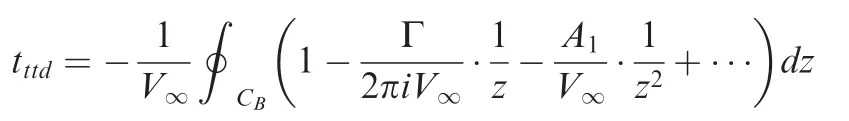
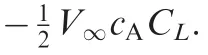
For infinitely thick airfoil,the transit time difference simply changes sign in comparison with that for infinitely thin airfoil,and is given by

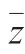
There exists some moderate value of thickness or angle of attack at which

Result C simply follows from Results A and B.In fact,a direct calculation shows that for a circular cylinder airfoil with any angle of attack Eq.(7) holds.

If the flow field on a grid is obtained either by conformal mapping or computational fluid dynamics,the transit times can be measured through using Tecplot,since Tecplot provides a timing tool,by which we can find the different times that a fluid particle has taken while arriving at a given point,such as the trailing edge.Table 1 shows a comparison between theory and numerical solutions for Joukowski airfoil with various angle of attack(α)and some thickness()and camber().The chord length is=1 m and the inflow velocity is=1 m/s.We see that when the thin airfoil assumption(small α，，) is met,the theoretical expression (4) compares well with numerical results.For very large α,the transit time indeed changes sign.For instance,when α=85,the transit time difference=2.89 s not only inverses its sign but also approaches the theoretical value 3.37 predicted by the infinitely thick airfoil expression (6).

Table 1 Comparison of transit time difference with theory and numerical results.

3.Significance of results

Result A means that,under thin airfoil assumption,fluid particles transit the upper surface at less time than those transiting the lower surface,in comply with Babinsky demonstration.Since the real flow as in Babinsky demonstration is viscous,it is interesting to check how the inviscid expression(4)applies to a viscous flow.For this purpose,we use CFD to compute the viscous flow around a NACA0012 airfoil,with α=5，=1 m，=1 m/s and a Reynolds number 10.CFD gives C=0.2112 and since the Kutta-Joukowski theorem also holds for unseparated boundary layer flow,the theoretical circulation can be evaluated as Γ=-C/2=-10.98,with which we should have=-0.00101 s by Eq.(4).Now we compare thiswith the measured one.Since the velocity vanishes on the body,should be measured near but outside the boundary layer.Fig.2(a)displays 4 sets of streamlines off the wall,along which=-0.000879，-0.00127，-0.001265，-0.00105 s. The first set enters into the boundary layer,the 2-4th are nearand outside of the boundary layer.The converged valueis close to -0.00127 s when approching the boundary layer and the 4th set has aclose to the theoretical.The positions(somewhere upstream of the stagnation point) and(crossing the trailing edge and perpendicular to the trailing edge streamline) are used as the starting and ending positions for transit time measurement.Increasingslightly does not changesignificantly since it is the transit time difference is measured.

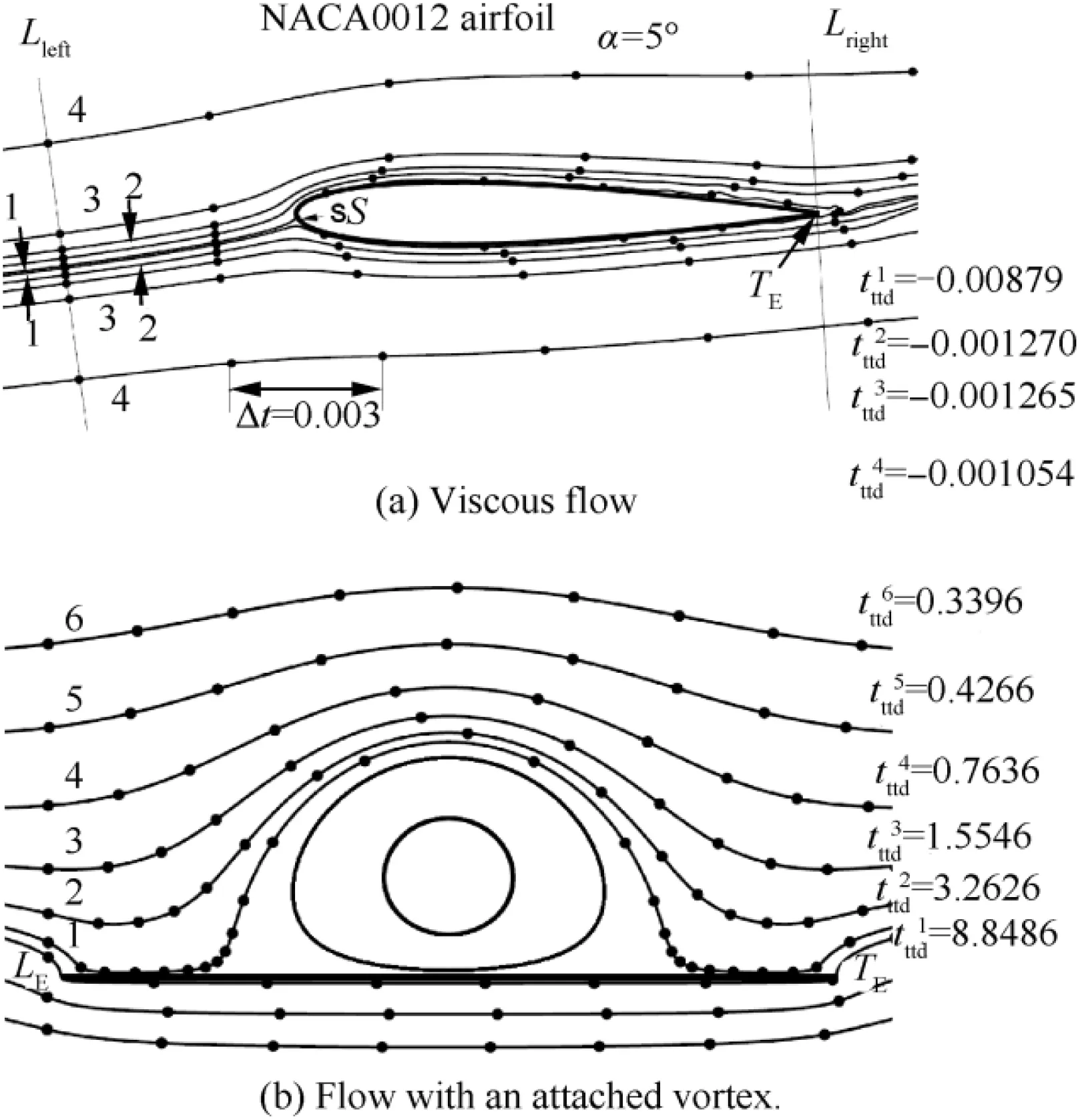
Fig.2 Transit time differences.

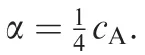
According to Saffmanand Saffman and Sheffield,if this vortex has a circulation Γ=-πthen this vortex is attached and the lift coefficient is C=2π＞0.For=0.5 m and=1 m,we observe from the time series displayed in Fig.2(b) that,along the streamline 1 which moves very closely to wall and passes over the vortex,air particles take much longer time than those moving below the plate.The transit time difference decreases when the distance of the streamline to the wall increases.This demonstrates one situation that the transit time difference changes sign comparing to thin airfoil situations.

The present work with transit time difference=t-tovercomes the difficulty of working with tand tindependently,since the theoretical values of tand tare infinite caused by the stagnation point.Previously,it was believed that air molecules moving on top of the airfoil takes less time than those below the airfoil.Here through the study of the transit time difference,we get the more complete picture that which of the air particles moving along the upper surface and lower surface arrive earlier at the trailing edge depends on the flow configuration and airfoil configuration (c.f.thickness and angle of attack).We have provided one situation (flow with an attached vortex) where the fluid particles take more time to transit the upper surface than the lower one,though the lift coefficient is positive.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

The authors are thankful to the Referees who provided valuable comments to improve the manuscript.This work was supported partly by the National Key Project of China (No.GJXM92579),the National Science and Technology Major Project of China (No.2017-II-003-0015),and the National Natural Science Foundation of China (No.11721202).