生长性学习：提升学生的认识

焦欢欢（江苏省南京市百家湖小学）

在数学教学实践中，以下现象屡见不鲜：教师稍微变化情境，学生便难以应对，这实质是学生的认知没有得到生长。教师需要转变视角，将焦点由“教知识”转变为“促生长”。因此，笔者倡导生长性学习，让教师的“教”真正引起学生认知的变化，让学生的生长“看得见”。作为教育者，应该以实现学生“生长性学习”为目标。为实现这一目标，笔者提出以下教学策略。

一、引导抽象思考：让学生的认识由感性生长为理性

学生思维发展的整体趋势是由具体到抽象，教师在呈现直观的材料后，还要引导学生进行抽象思考，让学生的认识由感性生长为理性。例如，在教学苏教版《义务教育教科书·数学》（以下统称“教材”）二年级下册“角的初步认识”时，教师通过逐步抽象，巧妙地让学生对“角”的认识走向理性。具体教学片断如下。

教师出示剪刀图、三角尺、时针和分针组成的角钟面图。

师：角在哪里？你们谁来指一指？

学生都指着剪刀头尖尖的部分。

生1：我认为这就是角。（生1摸着剪刀的一个顶点和两条边。）

师：你们能像这样找找三角尺上的角在哪里吗？钟面上的角呢？

学生在原有的认识上得到提升，正确地找出三角尺和钟面上的角。

师：仔细看，它们才真正是数学上的角。（教师出示图1。）

图1

师：比较一下，这些角有什么相同的地方？

生2：都有尖角。

生3：每个角都是由两条直直的线组成的。

师：它们都有自己的名称，自学教材内容。

自学后，学生总结：角是一个图形，有一个顶点和两条边。

教师的引导逐步抽象，让学生对“角”逐步上升到数学化的理性认识。由尖角、线这些直观的口语化表达，逐步上升到顶点、边这样抽象的数学化表达，从而认识到“角”的内核，使学生的认识由感性生长为理性。

二、聚焦本源知识：让学生的认识由模糊生长为清晰

很多学生知晓所学内容的结论，但是追问缘由却茫然不知，学生并没有清晰地认识到知识的本源。教师要聚焦本源知识，让学生的认识从模糊地记住结论走向清晰地理解知识的本质。例如，教材三年级下册“长方形和正方形的面积”这节课的教学片断。

师：请拿出事先准备的1平方厘米的小正方形，小组合作，摆出3个不同的长方形，把操作的结果填写在下表中。

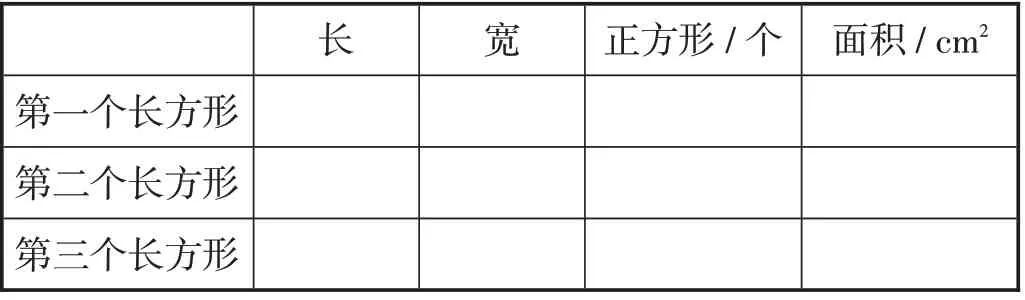
长 宽 正方形/个 面积/cm2第一个长方形第二个长方形第三个长方形

学生结合操作，交流相关数据。

师：图形的长和宽是怎么知道的？面积大小看什么？

生4：一排有几个，长就是几厘米，摆几排，宽就是几厘米。

生5：面积大小看正方形的个数，有几个1平方厘米的小正方形，面积就是几平方厘米。

师：如图2，如果这样铺，这个大长方形的面积是多少呢？

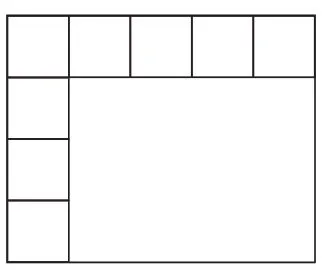
图2

生6：一排有5个，长就是5厘米，摆了4排，宽就是4厘米，5个4是20个，面积就是20平方厘米。

学生用小正方形动手验证。

师：如果长方形的长是7厘米，宽是2厘米，你能直接计算出它的面积吗？

生7：7×2=14（平方厘米）。长是7厘米，一排有7个，宽是2厘米，有2排，有2个7，面积是14平方厘米。

生8：我发现长方形的面积=长×宽。

师：为什么用长乘以宽表示面积？

生8：长是几，说明一排摆几个小正方形，宽是几，沿宽可以摆几排，长×宽=小正方形的个数。有几个1平方厘米的小正方形，面积就是几平方厘米。

本环节，教师聚焦本源知识设计操作活动，让学生建立一排的个数与长的关系、排数与宽的关系，感悟面积计算的本质是计算小正方形的个数，将长方形的面积与长和宽建立了联系，形成对面积计算的清晰认识。

三、提出深度问题：让学生的认识由浅层生长为深入

深度问题，是指能引发学生进行深度、从内在本质上思考的问题。一个有深度的问题恰似一盏明灯，指引学生的思维走向深邃之处。例如，教材六年级下册第94页“立体图形的复习”这节课的教学片断。

教师出示长方体、正方体、圆锥、球、圆柱。

师：哪些图形能与圆柱归为一类呢？

生9：我把圆柱、圆锥、球归为一类，因为它们都可以由一个平面图形旋转得到。

生10：我也把它们归为一类，因为它们从下面看都是圆。

师：这里用到了三视图的知识。（教师板书：三视图。）

生11：而且它们从中间平切，也都是圆。

师：也就是从截面看都是圆。（教师板书：截面。）

生12：我想把圆柱与长方体、正方体看作一类，因为他们的侧面积都可以用底面周长乘以高来计算。（教师板书：S侧=C底·h。）

在教学片断中，教师提出一个有深度的问题——“哪些图形能与圆柱归为一类呢？”，引发学生深度思考。学生思考：每种图形是怎样得到的？如何计算的？有哪些相同点？综观学生归类的理由：按照运动方式、计算方法、三视图、截面图等，可见学生对知识不是停留于浅尝辄止，而是深入到本质的理解。

四、暴露思维障碍：让学生的认识由错误生长为正确

教师要暴露学生的思维障碍，让学生心悦诚服地接受正确的认识，从而形成准确的认知结构。例如，教材二年级上册“厘米和米”第1课时“认识线段”这节课的教学片断。

师：两点之间能连几条线段？自己画试试。

教师收集了一些作品，如图3所示。

图3

生13：图3（1）不对，是连接两点，不能自己在线段中间画一个点。

生14：图3（2）也不对，上面画的不是线段，不是直的。

师：图3（3）呢？

生15：也不对，上面虽然是线段，却是一个点和上面点连起来了，不能在线段外面找点，只能是通过下面的两点去连接。

师：图3（4）呢？这两个点很大，所以能像这样连两条，可以吗？

生：不可以。

师：在数学上，点没有大小之分，如果把点看得足够大，像这样连了两条线段，实际上是把原来1个点分成了2个点（如图4），这样一来，两点之间有……

图4

生16：两点之间还是只有一条线段。

要想使学生真正改变自己错误的想法，就必须要让学生“看到”自己错误的认识。在两点之间能连几条线段的问题上，学生出现种种思维障碍，教师则大胆暴露，并引发全班学生交流辨析，让学生的认识由错误生长为正确。

教师不仅要关注学生的“学”，还要关注“学的变化”。生长性学习，关注学生认识的生长变化，强调变化路径的清晰、可视。教师可以通过引导抽象思考、聚焦本源知识、提出深度问题、暴露思维障碍等方式，明晰变化的路径，实现学生认识的拔节生长。