联系广义Kaup-Newell谱问题的一类方程的解

翟子璇，李 琪*，段求员，林清芳

(1.东华理工大学理学院，330013，南昌；2.抚州职业技术学院基础教学部，344000，江西，抚州)

0 引言

非线性科学是继相对论、量子力学之后自然科学界又一次新的大革命。而孤子理论作为应用数学和数学物理的重要组成部分，已然成为非线性科学中的一个重大研究课题。其中，寻求孤子方程的精确解是孤子理论中的一个重要专题，并已发展出诸多可行的方法，如齐次平衡原则[1]、反散射法[2-3]、Darboux变换[4]、Wronskian技巧[5-7]等。

本文将考虑耦合Gerdjikov-Ivanov(GI)方程

(1a)

(1b)

其所对应的谱问题：

联系广义Kaup-Newell谱问题[8]

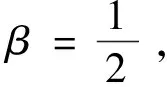
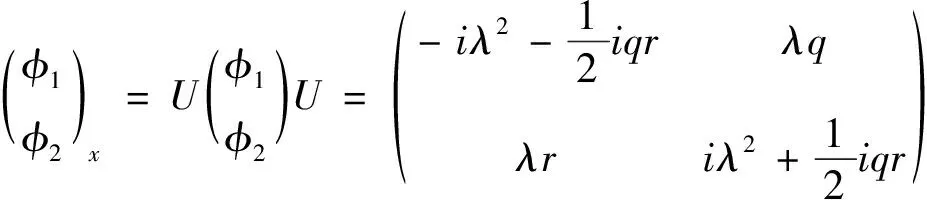
(2a)

时间发展式：

(2b)

其中，q=q(t,x),r=r(t,x)是位势函数，λ是x与无关的谱参数。

1 方程(1)的双Wronskian解

首先，对方程(1)作分式变换

(3)

则有方程(1)的双线性导数方程

(4a)

(4b)

(4c)

(4d)

定理1：双线性导数方程(4)有双Wronskian解

(5)

其中φj,ψj满足

(6a)

φj,t=2φj,xx,ψj,t=-2ψj,xx

(6b)

证明：

1)考虑谱问题(2a)与时间发展式(2b)。

令式(2a)中q=r=0，则

(7a)

即

φ1,x=-iλ2φ1,φ2,x=iλ2φ2

(7b)

再令(2b)中q=r=0，则

(8a)

也即

φ1,t=-2λ4φ1,φ2,t=2λ4φ2

(8b)

取k=-2iλ2,φ1=φ,φ2=ψ，则由式(7)与式(8)可知

(9a)

(9b)

2)计算双Wronskian行列式f,g,s与h对x的导数，得

又由式(9b)得f,g,s与h对t的导数，

将f,g及其关于x,t的各阶导数代入(4a)左端，根据恒等式：

以及行列式的性质：

① 设M为N×(N-2)矩阵，a,b,c与d都是N维列向量，则

|M,a,b||M,c,d|-|M,a,c||M,b,d|+

|M,a,d||M,b,c|=0

(10)

② 设aj,(j=1,2,…,N)是N维列向量，γj≠0,(j=1,2,…,N)是N个实常数，则

(11)

其中，γaj=(γ1a1j,γ2a2j,…,γNaNj)T。

可得：

=0。

故双Wronskian行列式(5)满足方程(4a)。同理可证，行列式(5)也满足式(4b)。

类似地，将f,g,s与h对x的各阶导数代入式(4c)，根据恒等式：

以及行列式的性质(10)与(11)。

得到：

=0。

故双Wronskian行列式(5)满足方程(4c)。同理可证，行列式(5)也满足式(4d)。

因此，方程(1)存在双Wronskian解

(12)

推论：双线性导数方程(4)有广义双Wronskian解

(13)

其中，φj,ψj满足

φj,x=Aφj,ψj,x=-Aψj

(14a)

φj,t=2φj,xx,ψj,t=-2ψj,xx

(14b)

其中，A=(aij)(N+M)×(N+M)是与t,x无关的任意实矩阵。而方程(1)的广义双Wronskian解为

(15)

2 孤子解与有理解

方程(14)有通解

φ=e2A2t+AxC,ψ=e-2A2t-AxD

(16)

其中，C=(c1,c2,…,cN+M)T,D=(d1,d2,…,dN+M)T是与t,x无关的任意常向量。

将式(16)展开成级数形式得

(17a)

(17b)

若A为对角阵，

(18)

将式(18)代入式(17)得

(19)

当N=M时，由式(19)构成的双Wronskian行列式f,g,s与h所确定的式(3)为方程(1)的N-孤子解。

若A为简单的Jordan阵，

(20)

且AN+M=0，故式(17)截断为

(21a)

(21b)

此时，φ与ψ的分量表达式分别为

(22a)

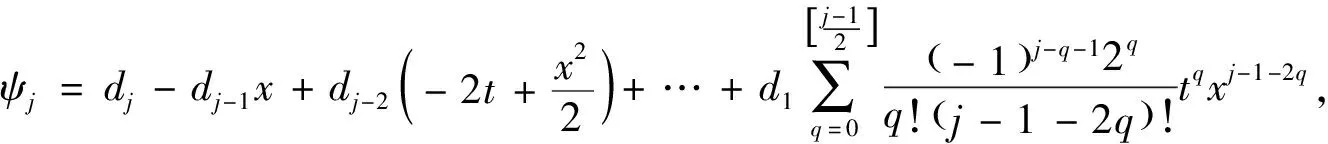
(22b)

由式(22)所确定的式(13)即为双线性导数方程(4)的有理解。

特别地，令c1=d1=1,ck=dk=0,(k=2,3,…,N+M)，由式(22)有

(23)

取j=1,2,3,4，得

当N=M=1;N=2,M=1;N=1,M=2;N=M=2时，双线性导数方程(4)的多项式解分别为

f=-1,g=1,s=-2x,h=4i;

f=2x,g=1,s=2(x2-2t),h=8i(x2+2t);

f=-1,g=2x,s=-2(x2+2t),h=4i;

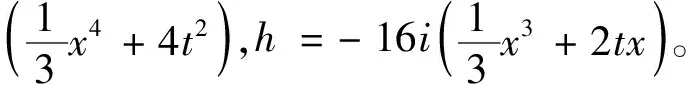
因此，方程(1)的有理解分别为

3 结束语

本文由广义Kaup-Newell谱问题得到耦合GI方程，并给出对应的双线性导数方程，进而利用Wronskian技巧求得耦合GI方程的广义双Wronskian解，包括孤子解及有理解，在后续的研究工作中，将继续探讨双Wronskian解的约化与Matveev解、Complexiton解以及混合解等更多精确解的导出。