“课程思政”视域下的高中数学教学思考
余铁青 祁云芳


【摘要】文章基于分析课程思政与高中数学学科教学的现实关系,思考了高中数学学科的思政教育功能,并举例给出了该视域下函数的概念教学思考,旨在通过该章节内容的教学设计,引起大家对课程思政视域下教学设计的更广泛思考.
【关键词】课程思政;函数的概念;教学设计
1“课程思政”的内涵与高中数学学科的内在现实关系
1.1“课程思政”概念的提出与内涵分析
习近平总书记在全国高等学校思想政治工作会议中强调:“要用好课堂教学这个主渠道,思想政治教育理论课要坚持在改革中加强,提升思想政治教育亲和力和针对性,满足学生成长发展需求和期待,其他各门课都要守好一段渠,种好责任田,使各类课程与思想政治教育理论课同向同行,形成协同效应.”[1]课程思政的内涵就是指将思想政治教育融入到课程教学的各个环节与显性思政教育协同构成立德树人的新模式.[2]这说明我们把原来思政教育的主阵地从单纯的思政课堂开始向多学科协同思政教育转变,我们开始认真思考如何将思政教育贯穿在具体的各学科教学中,并依托课程教学的多种有效组织形式向青年学子传播社会主义正能量,弘扬社会主义核心价值观,促进学生的身心全面发展,通过教书的手段最终达到育人的效果.
1.2“课程思政”与高中数学学科的内在现实关系
1.2.1高中数学“课程思政”是学科教育中立德树人的现实需要
中国高考评价体系中明确说到:高考的核心功能是立德树人,服务选才,引导教学.我们注意到此处把立德树人放在了首位,这就是高中数学学科教学的现实方向指引,我们通过数学学科的教学引导和启发学生让他们养成良好的品德,做到立德,另外通过数学学科的严谨表达,来培养学生的逻辑推理素养,科学精神素养等培育全面的人,实现树人的目标.现今高中生的生理发育虽然基本完成,但是心智很大程度上仍然是不够成熟,加之现代网络技术的高度普及,学生很容易通过媒体技术获取信息.在当前多元文化的冲击下,学生对社会的一些现象可能缺乏准确的认识.因此在数学学科中渗透思政教育这项工作具有深远意义.
1.2.2高中数学学科教学改革的必然趋势
在全国高等学校思想政治工作会议后,全国各高等院校教师就开始了非常广泛的研究,但基本上还是集中于高等教育阶段从不同的专业课程里面去渗透思政思想.而高中数学作为高中教育阶段的最主要的学科之一,我们能不能从课程的授课内容中去设计,找准知识内容的切入点,植入思政教育素材,向学生渗透思政教育呢?实际上,这种想法其实不难实现,而且有相当的可操作性.数学作为社会发展的工具性学科,它本身就具有相当的抽象性、复杂性、严密性等特点,它的发展凝聚了大量科学家的心血.数学家通过不懈努力,发现了一些特殊的规律和客观的事实,我们把这些内容以定理和性质的形式进行给出.然而这些相关定理、性质的生成都是数学家经过严谨的推理证明而来,这本身就是一种艰苦奋斗的精神写照,这其实就是最简单、最朴素的思政教育素材,加之数学学科所特有的逻辑严密性发挥着数学学科的育人作用,因此,挖掘数学学科课程的思政素材、发挥数学学科的协同育人功能是为数学教育锦上添花.通过在授课中传播渗透这些积极的思想观念,让学生成长为社会主义的坚实守护者和可靠接班人,因此数学学科不仅有着重要的育人价值,也有立德树人的教育使命.
1.2.3高中数学学科知识特性与思政的辩证统一
高中数学的教学首先是服务于高考,但高考数学考的不仅仅是数学知识,考查的应该是更深层次的马克思主义的认识论问题.如果说数学知识本身的积累有助于学习者通过运用知识来解决实际问题,给决策提供有力支持,那么辩证思维的力量则是方向的把控问题,是思考方式的问题[3].从高度上看,数学高考试题的命制在考查知识的同时更应注重辩证思维的渗透,思维方式的引领,这实质是一种辩证的唯物主义美学潜移默化的影响.比如我们所谈到的函数里面的对应思想,这与我们生活中的变与不变,量变与质变等相互交织在一起,浑然天成,再如这几年依托于空间立体几何情境所命制的数学文化试题有助于发展学生的爱国主义情操,这就是数学学科与思政的内在统一性.
2基于课程思政下函数的概念教学设计分析
2.1教材分析
函数的概念是继学习集合概念之后的一个抽象概念,我们进一步运用集合与对应的观点来刻画函数,突出了函数是两个集合之间的对应关系,注重领会集合思想、对应思想和模型思想.因此该课时的重点应放在函数的概念理解上,通过生活中的实际事例,引出函数的定义.
2.2学情分析
刚进入高中的学生,抽象能力不强.但函数的概念内容本身就比较难,使得学生对概念的记忆和理解更加不易.因为函数概念本身的特殊性,这个章节是非常重要的,假设这个章节没有理解清楚,以后就会难以深入理解函数的性质等内容,因此一定要帮助学生深入理解函数本质.
2.3教学重难点
教学重点:根据实际例子来刻画函数模型,抽象函数概念.
教学难点:函数本质属性的解读以及辅助学生主动建构生成函数的概念.
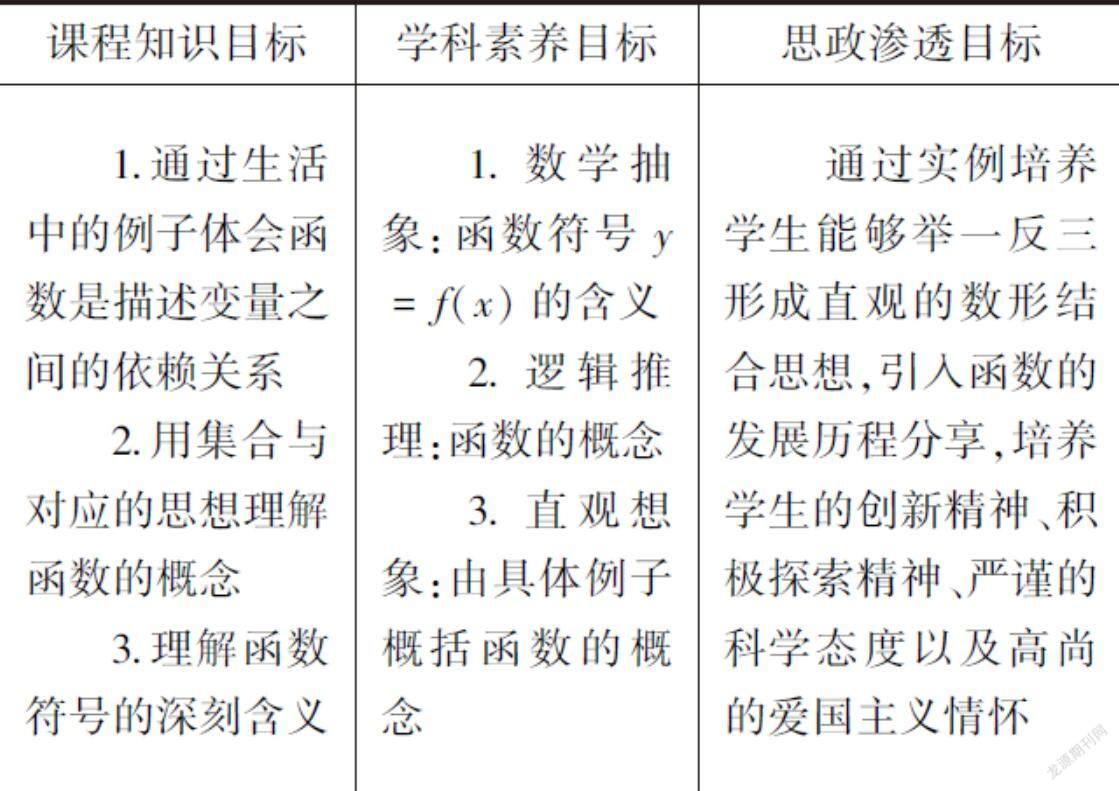
2.4教学目标和核心素养以及课程思政渗透:
3基于课程思政下“函数的概念”教学设计
3.1情境引入
师:实际上函数的发展也并不是静止的,随着数学使用的不断发展,函数的概念也慢慢在改进和精准化,逐步达到完善.那大家想不想知道函数的概念的发展史呢?
师:那好,下面我就来带领大家一起看看函数概念的发展历程[46].(PPT投影)
师:从函数概念的发展史让我不禁想到近代国外的强國之所以强大是因为其科学技术的高度发展,试想我们国家的古代数学文化是何等的灿烂辉煌,我们的九章算术,割圆术等等都是遥遥领先于外国.近代以来,我们国家还停留在清王朝人家就已经开始进行工业革命,这很好地诠释了落后就要挨打的道理.事实证明:为了中华民族的伟大复兴,努力学习科学文化知识是必由之路!
设计意图通过介绍函数概念的演变发展历程,从学生最近发展区入手,为深入学习更加深刻的函数概念做好铺垫.比对这些数学家的国籍,我们不难明白,他们这些国家的科技发展迅速主要也是依赖于数学本身的工具性所做出的贡献,从而延伸到我们中华民族的伟大复兴,调动学生的学习积极性,培养学生积极探索的科学精神,培养学生高尚的爱国主义情怀.
3.2合作探究,发现新知
问题1某“复兴号”高速列车到350 km/h后保持匀速运行半小时.这段时间内,列车行进的路程S(单位:km)与运行时间t(单位:h)的关系可以表示为S=350 t.[7](同时播放中国复兴号高铁经过本市高铁车站的视频短片)
设计意图依托高铁背景,逐渐渗透区间表达下的定义域与值域的初级形式,注意此处的定义域和值域都是连续型.另外从思政角度,学生在掌握知识的情况下领略到国家高铁事业发展的波澜壮阔,激发民族自豪感,强化爱国主义情怀.
问题2某电气维修公司要求工人每周工作至少1天,至多不超过6天.如果公司确定的工资标准是每人每天350元,每周付一次工资[7],那么你认为该怎样确定一个工人每周的工资?一个人的工资w(单位:元)是他工作天数d的函数吗?
设计意图标准的一对一,这将问题1中的定义域与值域问题进行了变化,由连续型转变到了离散型,体现了自变量的变化范围的多样性.从思政角度而言就是依据工人劳作获得报酬,赞扬了我国劳动人民艰苦奋斗、吃苦耐劳的民族精神,引导青年学生要脚踏实地、积极进取.
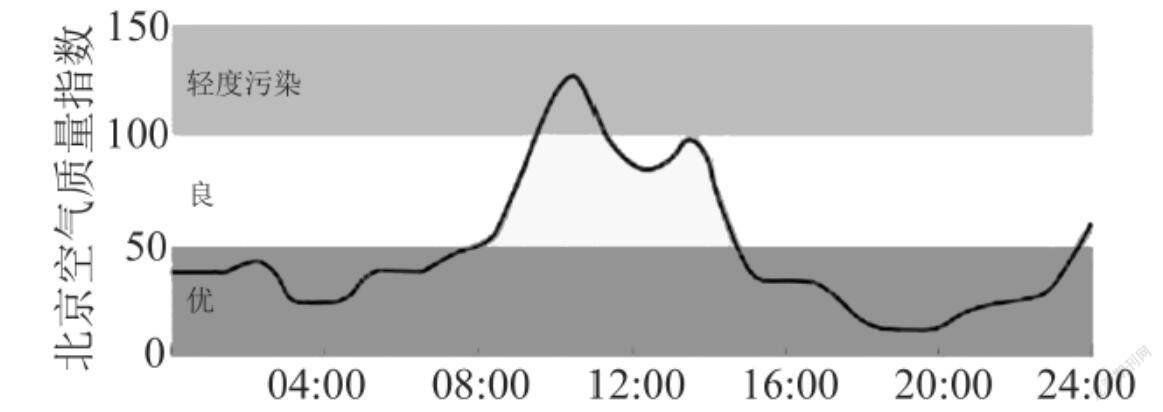
问题3下图是北京市2016年11月23日的空气质量指数变化图[7].设计意图在引导学生从显性函数表达解析式的角度逐渐过渡到隐形函数关系的表达,从思政角度而言就是引导学生注重节能减排,树立环保意识,启发学生加强生态文明建设.
问题4国际上常用恩格尔系数
r(r=食物支出金额总支出金额×100%)
反映一个地区人民生活质量的高低,恩格尔系数越低,生活质量越高.下表是我国某省城镇居民恩格尔系数变化情况,从表中可以看出,该省城镇居民的生活质量越来越高[7].
设计意图 通过展示表格,学生在强化函数直观理解的基础上,发现随着年限往后,恩格尔系数在减小的规律,这就引导学生认识到生活水平在实打实地提高,坚定信念紧跟共产党的领导,提升对国家的执政自信.
3.3引导学生从直观依赖关系过渡到逻辑对应关系
师:为了更加客观理性地描述以上四个问题,请大家讨论一下能不能用比较统一的对应关系来描述一下大家所讲的依赖关系呢?
设计意图通过辨析依赖与对应的区别,培养学生严谨的学习态度,和勇于探索的精神.
3.4函数的对应关系转变到集合的对应关系
师:我们整理一下刚才大家的发言(PPT同步板书):函数的概念:设A,B是非空的数集,如果按照某个确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数y和它对应,那么就称f:A→B为从集合A到集合B的一个函数(function),记作:y=f(x),x∈A.其中x叫做自变量,x的取值范围A叫做函数的定义域;与x的值相对应的值y叫做函数值,函数值的集合{f(x)|x∈A}叫做函数的值域.
设计意图引导学生自主归纳总结,引领学生感受数学的推理总是从特殊到一般的变化规律,也能够促进学生加深自身的自我认同,凸显由量变到质变的哲学思维,提升学生的思辨能力.参考文献
[1]习近平在全国高校思想政治工作会议上强调把思想政治工作贯穿教育教学全过程,开创我国高等教育事业发展新局面[N].人民日报,20161209(01版).
[2]习近平主持召开学校思想政治理论课教师座谈会强调用新时代中国特色社会主义思想铸魂育人,贯彻党的教育方针落实树德立人根本任务[N].人民日报,20190319(01版).
[3]吴新华,余铁青.辩证思维美学在高考数学试题中的渗透分析\[J\].中学数学研究,2021(16):4547.
[4]李鹏奇.函数概念300年\[J\].自然辩证法研究,2001(03):4852.
[5]萧昌建.人文数学导引\[M\].成都:西南交通大学出版社,2006:8086.
[6]汪晓勤,韩样临.中学数学中的数学史\[M\].北京:科学出版社,2002.
[7]人民教育出版社,课程教材研究所,中学数学课程教材研究开发中心.普通高中数学教科书必修第一册\[M\].北京:人民教育出版社,2019:6062.
作者简介余铁青(1990—),男,江西景德镇人,硕士,中学一级教師,中国数学会会员,广东省方亚斌名师工作室成员,广东省第二批STEM教改实验教师;主要研究高中数学教育教学理论;发表论文40余篇.
祁云芳(1975—),女,湖南益阳人,中学高级教师,中山市优秀教师,辅导学生多人数学竞赛获奖.

