数学问题解答

2021年12月号问题解答

(解答由问题提供人给出)

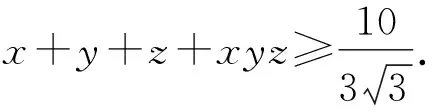
(浙江湖州市双林中学 李建潮 周秋斓 313012)

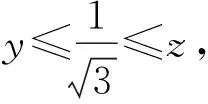
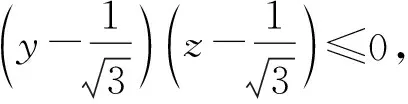
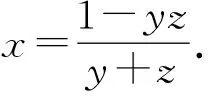
x+y+z+xyz=y+z+1+yzx

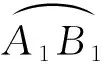
(北京师范大学附属实验中学 白玉娟 100032；北京市朝阳区郎各庄村21号 郭 璋 100121)

证明如图，在⊙O中，弦A1B1=A2B2且A1B1∥A2B2，易证四边形A1A2B2B1为矩形，所以直线CA1A2平行于直线DB1B2，又直线EF2垂直于直线A1B1，从而直线EG1F1G2F2平行于直线CA1A2、直线DB1B2.所以

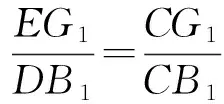
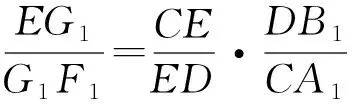
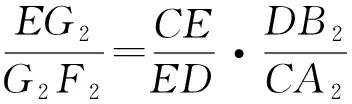
由③+④得

把上式两边分别平方得

因为CD为过点E的⊙O的切线，所以有CE2=CA1·CA2,ED2=DB1·DB2，进而有

所以

2638在△ABC中,三边长为a,b,c,面积为Δ,且外接圆与内切圆半径分别为R,r,则

(1)

(天津港职工培训中心 黄兆麟 300456)

证明注意到有熟知的Finsler—Hadwiger不等式的最佳式

(2)

注意到有内切圆半径公式

而以上最后一式是熟知的Garfunkel—Bankoff不等式,故(2)式成立,从而不等式(1)成立.

2639如图，已知在△ABC中，∠ACB=90°，点D在AB上，且(CD·AB)2=2CA·AD·DB·BC.求证：CD平分∠ACB.

(江苏省溧阳市光华高级中学 钱德全 213300;江苏省溧阳市永平小学 张晓蔚 213333)

证明如图，作DE⊥BC于E，DF⊥AC于F.因为∠ACB=90°，所以四边形CEDF为矩形，所以DE∥FC，DE=FC，DF∥EC，DF=EC.

得m2+n2=2mn，即(m-n)2=0，

所以m=n，因此四边形CEDF为正方形，

故有CD平分∠ACB.

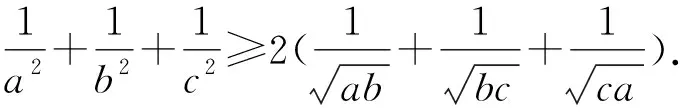
(江西省共青城市国科共青城实验学校 姜坤崇 332020)

证明条件式ab+bc+ca+2abc=1

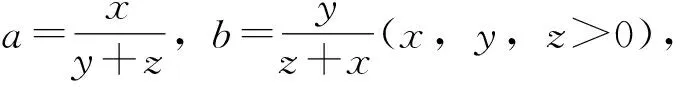
于是所证不等式可化为

由二元均值不等式得

①

又由二、三元均值不等式得

②

由①、②式即得

从而所证不等式成立.

2021年1月号问题

(来稿请注明出处——编者)

2641已知△ABC的外接圆过点B、C的切线交于点P,延长BA至点D,使AD=AB,作DE∥BC交直线PB于点E.求证:

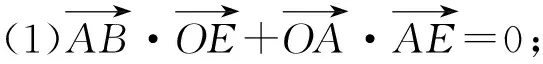
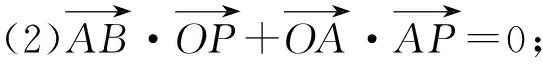
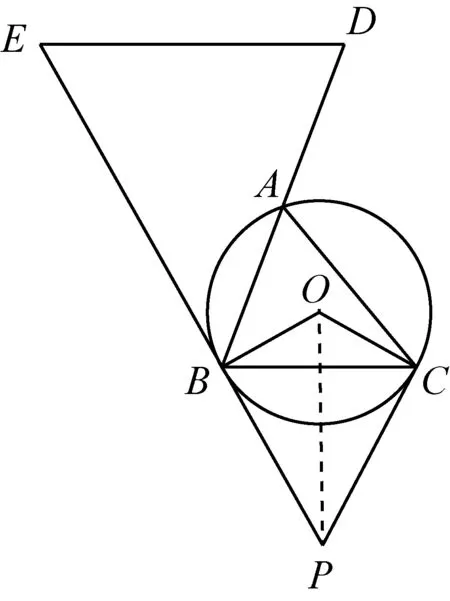
(华中师范大学国家数字化学习工程技术研究中心 彭翕成 430079；山西省临县一中 李有贵 033200)

2642已知a,b,c,d≥0,a+b+c+d=1,且

求p的最大值.

( 陕西省咸阳师范学院教育科学学院 安振平 712000 )

2643设双曲线C的两焦点为F1、F2，两准线为l1、l2，过双曲线上一点P，作平行于F1F2的直线，分别交准线l1、l2于M1、M2，直线M1F1与M2F2交于点Q，则P、Q、F2、F1四点共圆.

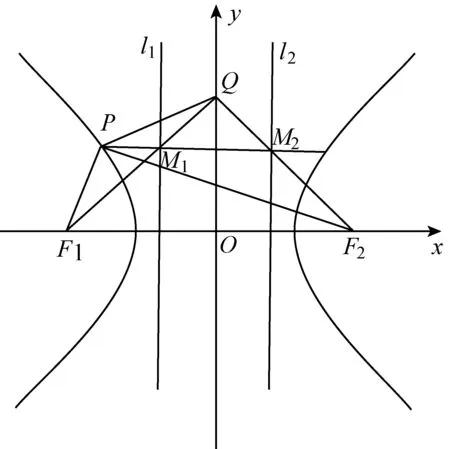
(江西省都昌县第一中学 刘南山 332600)

2644在三角形ABC中，求证:

cosAcosB+cosCcosA+cosBcosC

(山东省单县园艺中心校 张建平 274300)

2645如图，△ABC中，直线AP,BP,CP分别与各自对边所在的直线交于点D,E,F．

(i)求使得

的所有点P；

(ii)求使得

S△PBD+S△PEA=S△PDC+S△PAF=S△PCE+S△PFB

的所有点P.

(重庆市长寿龙溪中学 吴波 401249)