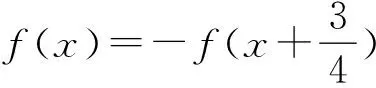近40年高考全国卷中周期性问题的梳理及启示
王克亮
(江苏省射阳中学 224300)
为研究高考全国卷中的周期性问题,笔者人工检索了1981~2020年由教育部考试中心命制的高考数学试卷203份,加上近期2021年高考的6份全国卷,共摘录了与周期性有关的试题47道,将它们按“年份、题号、题型、难度、考查函数、设问角度”这几个栏目制作成表格(受篇幅限制,此略),然后对此作了统计与分析,从中获得了一些启示.
1 考情分析

表1 考查年份统计表
由表1可知,自1985年首次考查周期性问题以来,只有90年、02年、07年这3年没有出现与周期性直接相关的试题,其余年份均有涉及,年份的考查率达91.89%(不含81年~84年). 其中,2008年至今,该知识点的考查一直没有间断过.

表2 考查题型统计表
由表2可知,周期性问题的考查题型包括选择题、填空题和解答题,其中选择题(含多选题)36道,占比76.59%;填空题6道,占比12.77%;解答题5道,占比10.64%. 2020年首次出现多选题,1998年曾以填空题形式出现过多选题. 另外,近十多年来没有在解答题中考查过该问题.

表3 试题难度统计表
由表3可知,周期性试题以容易题和较易题为主,共26道,占比55.32%;中档题17道,占比36.17%;较难题4道,占比8.51%. 值得注意的是,2011年之后的19道试题中,属中档题与较难题的有15道,占比为78.95%,可见对周期性问题考查的要求在明显提升.

表4 考查的函数类型统计表
由表4可知,考查的函数类型以三角函数为主体,共37道,占比78.72%;一般函数4道,占比8.51%;抽象函数6道,占比12.77%. 值得注意的是,对三角函数周期性的考查,从最初的直接代公式求解,到后来的先进行三角变换再代公式求解,再到目前的通常将周期性与函数图象、单调性、最值、对称性等性质融合在一起进行考查. 另外,2011年之后的19道试题中,以一般函数或抽象函数为载体的有6道,占比31.58%,该比例在明显提升.
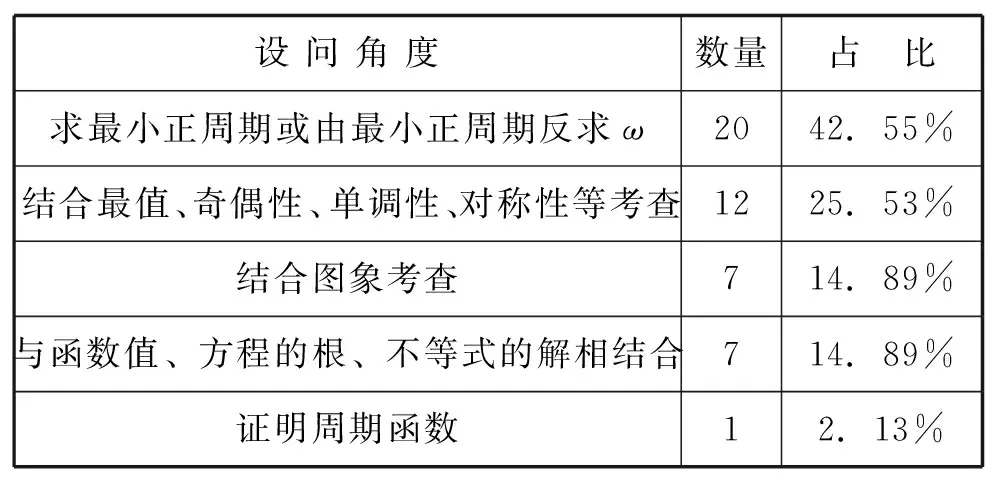
表5 设问角度统计表
由表5可知,周期性问题的设问角度,求最小正周期或由最小正周期反求ω的,有20道,占比42.55%;结合最值、奇偶性、单调性、对称性等性质考查的12道,占比25.53%;结合图象考查的7道,占比14.89%;与函数值、方程的根、不等式的解相结合的7道,占比14.89%;证明周期函数的1道,占比2.13%. 值得注意的是,2011年之后的19道试题中,单纯求三角函数最小正周期的只有3道,试题的综合性明显加强.
综上所述,近40年高考全国卷中周期性问题的考情如下:
(1)考查周期性问题的年份率达90%以上,且2008年至今没有间断过;
(2)涉及周期性问题的题型比较多样,选择、填空、解答都有可能,2020年又出现了多选题;
(3)试题的难度在加大,近年来以中档题与较难题身份出现的比率近80%;
(4)以三角函数为考查主体,近年来以一般函数或抽象函数为载体的试题的比率在提高,接近三分之一;
(5)试题由以前比较单一的求三角函数的最小正周期问题,逐步趋向与函数图象和其它性质进行融合,试题的综合性在加强,对考生能力的要求进一步提升.
2 解决策略
解析了上述高考试题,得到周期性问题的常用解决策略有如下几种.
2.1 化归基本模型
与三角函数有关的周期性问题,通常可化归为基本的三角函数模型,再代入周期公式来解决问题,转化的手段是三角变换.

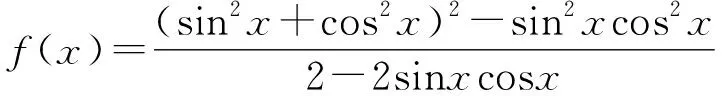

评注将所给函数转化为基本的三角函数模型(如y=Asin(ωx+φ)+k,y=Acos(ωx+φ)+k,y=Atan(ωx+φ)+k,等)是常用的处理手法,以便于代入周期公式来解决问题.

A.f(x)=|cos 2x| B.f(x)=|sin 2x|
C.f(x)=cos|x| D.f(x)= sin|x|

评注几种加绝对值的三角函数也属于基本的模型,如y=|Asin(ωx+φ)|(周期变为原来的一半),y=sin|x|(非周期函数),y=cos|x|(周期不变),等.在上述梳理出的高考试题中,有5道涉及到加绝对值的三角函数.
2.2 把握性质关系
解决三角函数的周期性问题时,要把握三角函数的性质与性质之间的关系,以及图象与性质之间的关系,善于从题中所给的函数图象或性质中转化得到周期的信息.


图1




评注本方法是将所给函数图象的特征转化为相位的大小来解决问题的.

A.11B.9 C.7 D.5




评注本方法是运用了函数的零点与对称轴之间的距离与周期之间的关系,以及函数单调区间的长度与周期之间的关系来解决问题的.
结论一般地,函数y=Asin(ωx+φ),y=Acos(ωx+φ)性质之间具有如下关系:
(1)对称轴必定经过它们的极值点;
(2)相邻两个零点的中点必为极值点,相邻两个极值点的中点必为零点;
(3)相邻的零点、相邻的对称轴间的距离均为半个周期;
(4)相邻的零点与极值点间的距离为四分之一个周期;
(5)极值点间、零点间的距离均为半个周期的正整数倍;
(6)零点与对称轴间的距离为半个周期的正整数倍与四分之一个周期的和;
(7)一个单调增区间(或减区间)的长度不超过半个周期;
(8)零点(或极值点)在一个周期中的位置与相应的相位对应;等等.
2.3 熟悉定义拓展
我们知道,周期函数f(x)定义的核心是满足恒等式f(x+T)=f(x),x∈A,其中T为非零常数,A为函数f(x)的定义域.该恒等式合理延伸后,可得到一些拓展结论.理解这些拓展结论的内涵,将有助于我们解决周期性问题.

(2)证明f(x) 是周期函数(此处略去(1)和(3)).
解析因为y=f(x)关于直线x= 1对称,所以f(x) =f(2-x),x∈R.
又因为f(x)是偶函数,所以f(x) =f(-x) ,x∈R,所以,f(-x) =f(2-x) ,x∈R.
将上式中“-x”用“x”来代换,得f(x) =f(x+2),x∈R.这表明f(x)是R上的周期函数,且2是它的一个周期.
案例6(2018年普通高等学校招生全国考试理科卷2第11题)已知f(x)是定义域为(-∞,+∞)的奇函数,满足f(1-x)=f(1+x),若f(1)=2,则f(1)+f(2)+f(3)+…+f(50)=( ).
A.-50 B.0 C.2 D.50
解析因为f(x)是奇函数,所以f(x)=-f(-x).又因为f(1-x)=f(1+x),即f(x)=f(2-x),所以-f(-x)=f(2-x) ,即f(2+x)=-f(x),所以f(x+4)=-f(x+2)=f(x),所以函数f(x)是以4为周期的周期函数.
根据周期性,以及f(0)=0,f(1)=2,可得f(1)+f(2)+f(3)+…+f(50)=2.故选C.
评注这两题都是运用了周期函数的定义及其拓展结论来解决问题的.
结论(1)一般地,在下列条件下,可得到对应函数为周期函数:
(I)知一个恒等式的(其中a≠0,k≠0)
比如,f(x+a)=f(x)(T=a);f(x+a)=-f(x)(T=2a);f(x+a)=f(x-a)(T=2a);
f(x+a)=-f(x)+k(T=2a);fn(x+a)+fn(x)=k(f(x)>0)(T=2a);

(II)知两个对称性的
比如,①若函数f(x)的图象关于直线x=a与x=b(b>a)对称,则f(x)是以2(b-a)为周期的周期函数;
②若函数f(x)的图象关于点(a,0)与点(b,0)(b>a)对称,则f(x)是以2(b-a)为周期的周期函数;
③若函数f(x)的图象关于直线x=a与点(b,0)(b>a)对称,则f(x)是以4(b-a)为周期的周期函数;等等.
(2)反之,由周期性和一个对称性可得到其它的对称性.
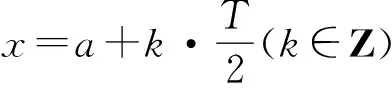

2.4 借鉴周期思想
有些函数虽不是周期函数,但其性质类似于周期函数,这时我们可借鉴周期思想来解决问题.

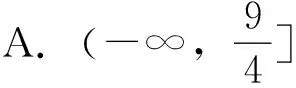


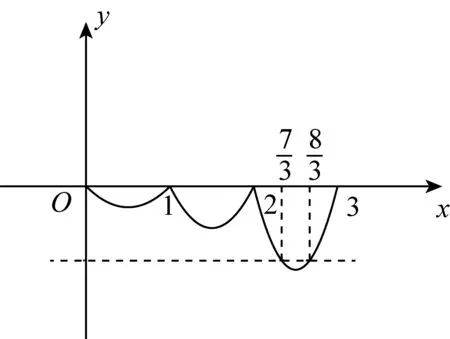
图2
评注当函数满足f(x+T)=Af(x)(T,A≠0)、f(kx)=Af(x)(k,A≠0)等恒等式时,该函数将呈现类周期性.
3 命题警示
因为函数的周期性与其对称性等性质既相互关联,又相互制约,所以命题时一不小心就会出现多余的或自相矛盾的条件,从而犯科学性错误.
案例8(2005年某省高考试题)已知f(x)是R上的以3为周期的奇函数,且f(2)=0,则方程f(x)=0在区间(0,6)内解的个数的最小值是( ).
A.2 B. 3
C. 4 D. 5

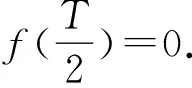

f(1)+f(2)+f(3)+…+f(2010)=________.