20世纪初美国代数教科书中的数学史
汪晓勤
(华东师范大学数学系 200241)
1 引 言
我们在19世纪以前的数学教科书中很少见到数学史的影子.事实上,以蒙蒂克拉(J. E. Montucla, 1725—1799)、康托(M. Cantor, 1829—1920)等为代表的早期数学史家,并非为了教育而去研究数学史,数学史的教育价值远未受到人们的普遍关注,即使是在今天,数学史研究者大多也仍不关注自己所研究主题的教育价值.另一方面,绝大多数教科书编写者对相关领域的历史不甚了了,且数学教育领域与数学史领域的学者之间很少有思想交流,导致大多数数学教科书与数学史之间存在很深的鸿沟.
然而,在19世纪末,以史密斯(D. E. Smith, 1860—1944)和卡约黎(F. Cajori, 1859—1930)为代表的美国数学史家改变了数学史被教科书冷遇的现状.史密斯和卡约黎既是数学史家,也是数学教育家,对于数学史的教育价值有着深刻的认识.史密斯是国际数学教育委员会的创始人,曾先后担任该委员会的副主席(1908—1920)和主席(1928—1932),卡约黎则先后担任了全美教育协会“十人委员会”成员(1892)、美国几何大纲“十五人委员会”成员(1910—1913).与前辈蒙蒂克拉和康托不同,他们撰写数学史的主要目的是为数学教育服务.他们利用自己在数学史方面的学术优势,在各自参编的数学教科书中较多地运用了数学史素材.史密斯和卡约黎对同时代的其他教科书编者产生了较大的影响.
我们选择20世纪前20年间在美国出版的11种代数教科书(Beman & Smith, 1900;Young & Jackson, 1908a; Young & Jackson, 1908b;Durell, 1912;Young & Jackson, 1913;Cajori & Odell, 1915;Slaught & Lennes, 1915;Cajori & Odell, 1916;Hallett & Anderson, 1917;Wentworth, Smith & Brown, 1917;Schultze, 1918),对其中的数学史材料进行考察,试图回答以下问题:11种代数教科书运用了哪些数学史料?有何特点?它们又是如何运用这些史料的?
2 教科书中的数学史材料
2.1 名人名言
Slaught & Lennes (1915)在扉页中引用培根(R. Bacon, 1214—1294)的话来强调数学的价值.
· “一切科学最终都依赖于数学.”
· “数学应被看做一切哲学的基础.”
· “只有神圣的数学,能够净化人的心智,使学生得以获取一切知识.”
不过,在其他教科书中很少见到名人名言.
2.2 数学词源
Beman & Smith (1900)在附录中,给出了全书涉及的数学术语的词源分析表,帮助学生更好地理解这些术语.表1给出了其中一些重要术语的词源分析.

表1 Beman & Smith(1900)中的部分数学术语词源
在数学教科书中补充数学名词的词源分析,这是编写者贝曼(W. W. Beman, 1850—1922)和史密斯的一项创举.
2.3 数学人物
Beman & Smith (1900)在附录中扼要介绍代数学的历史之后,收录了书中出现的43位数学家的生卒年和简介.Cajori & Odell (1915,1916)使用了韦达(F. Viète, 1540—1603)、笛卡儿(R. Descartes, 1596—1650)、沃利斯(J. Wallis, 1616—1703)、牛顿(I. Newton, 1643—1727)、欧拉(L. Euler, 1707—1776)和德摩根(A. De Morgan, 1806—1872)的画像,画像之下配有简要的文字介绍(图1).
Slaught & Lennes (1915)使用了魏德曼(J. Widmann, 1462—1498)、韦达、哈密尔顿(R. Hamilton, 1805—1865)、牛顿、毕达哥拉斯、沃利斯、笛卡儿、高斯(C. F. Gauss, 1777—1855)和帕斯卡(B. Pascal, 1623—1662)的画像(图2).画像之下附有简单的生平介绍.
Hallett & Anderson (1917)使用了毕达哥拉斯、欧几里得、韦达、帕斯卡、笛卡儿、牛顿、高斯的画像,画像之下配有简单的生平介绍.

图1 Cajori & Odell (1915; 1916) 中的数学家画像

图2 Slaught & Lennes (1915)中的数学家画像
2.4 图片资料
图片资料指的是历史上数学书籍(包括手稿)的书影、历史上天文学家和数学家所使用的测量工具图片、反映数学主题的绘画作品等.
Wentworth, Smith & Brown (1917)代数部分给出雷科德《砺智石》中出现“等号”的一页书影(图3)、魏德曼算术书中的加减号(图4)、16世纪数学书中代数式的写法(图5)、花拉子米《代数学》拉丁文译文的手抄本书影(图6)等.

图3 等号的创用(《砺智石》,1557) 图4 加减号的创用(魏德曼算术,1489)

图5 一次多项式的加法(格兰迈特乌斯,1518) 图6 花拉子米《代数学》抄本(1456)
在与史密斯合作之前,美国数学家温特沃斯(G. A. Wentworth, 1835—1906)在其独立编写的各种数学教科书中,未曾使用过任何数学史料.而作为著名的数学史家,史密斯无论是在课堂教学中还是在编写教科书时,都十分重视有关数学历史文献的图片,由于他拥有丰富的藏书,因而可以自由地使用相关的图片.
2.5 数学问题
数学的历史为教科书提供了取之不尽、用之不竭的问题.Beman & Smith(1900)在“一元一次方程”一章,呈现了数学史上的10个问题,具体见表2.

表2 Beman & Smith(1900)中的历史问题
Young & Jackson (1908a)采用了14世纪数学手稿以及17—18世纪法国数学家奥泽南(J. Ozanam, 1640—1718)、英国数学家桑德森(N. Sanderson, 1682—1739)、辛普森(T. Simpson, 1710—1761)和19世纪英国数学家布兰德(M. Bland, 1786—1868)有关著作中的数学问题,如:
· 今有3个酒桶,总容积为79加仑.第二个酒桶比第一个酒桶的一半多了3加仑,第三个酒桶比第二个酒桶少7加仑.问:每个酒桶的容积各为多少加仑?(14世纪数学手稿)
· 甲对乙说:“若你给我3个硬币,则我的硬币和你一样多.”乙回答说:“若你给我3个硬币,则我的硬币是你的两倍.”求甲、乙各有硬币数.(奥泽南《代数基础》,1702)
· 若干人在酒馆付账.他们发现,若增加3人,则每人各少付1先令;若减少两人,则每人需多付1先令.求原来的人数和账款.(桑德森《代数基础》,1740)
· 7年前,某人的年龄是其儿子的4倍;7年过去了,他的年龄变成儿子年龄的2倍.求父子的年龄.(辛普森《代数专论》,1767)

Young & Jackson (1908b)采用了法国数学家奥泽南、克莱罗(A. Clairaut, 1713—1765)和英国数学家牛顿(I. Newton, 1643—1727)等的数学问题,如:
· 信使从巴黎出发去格勒诺布尔,两地相距120里,共用了4天时间.从第二天开始,每一天比前一天少走2里.问:每天各走几里?(奥泽南《代数基础》,1702)
· 甲单独完成a单位工作量,需b单位时间;乙单独完成c单位工作量,需要d单位时间;丙单独完成e单位工作量,需要f单位时间.问;三人一起完成g单位工作量,需要多长时间? (克莱罗《代数》,1746)
· 甲、乙两地相距59英里.A和B各从甲地和乙地出发,相向而行.B比A迟1小时出发.A2小时走7英里,B3小时走8英里.问:A与B相遇时,A走了多远? (牛顿《广义算术》,1707)
Young & Jackson (1913) 采用了18世纪英国数学家桑德森、瑞士数学家欧拉和法国数学家波素(C. Bossut, 1730—1814)的数学问题:
· 甲、乙、丙各欠某人若干镑.已知甲、乙共欠60镑,甲、丙共欠80镑,乙、丙共欠92镑.问:甲、乙、丙各欠多少镑?(桑德森《代数基础》,1740)
· 一座房子值钱100元.若A除了自己的钱外,还拥有B的钱的一半,B除了自己的钱外还拥有C的钱的三分之一,C除了自己的钱外还拥有A的钱的四分之一,他们各自就能买得起这座房子.问:A、B、C各有多少钱?(欧拉《代数基础》,1770)
· 一个装满水的容器共有A、B、C三个排水孔.若三孔同开,则6小时排空;仅用B孔排空容器所需时间是仅用A孔所需时间的3/4倍;仅用C孔排空容器所需时间是仅用B孔所需时间的两倍.问:各排水孔单独排空容器,各需多长时间?(波素《代数基础》,1773)
Schultze (1918) 在全书最后给出1012道复习题,其中有三题源于数学史:
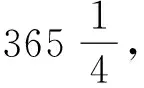
· 完满数指的是与所有真因数之和相等的数.若数列20,21,22,…,2n的和为素数,则该数乘以数列的最后一项,结果为完满数.(欧几里得)试求出4个完满数.
· 一则阿拉伯传说指出,象棋是由一位名叫赛萨的人为娱乐印度国王希兰而发明的.这位国王承诺奖赏发明者:在棋盘的第一格放1粒麦子,在第二格放2粒,在第三格放4粒等等,后一格的麦粒数是前一格的两倍.试求赛萨将要获得的麦粒数.
2.6 专题历史
数学专题的历史通常以注解的形式出现,主要追溯某个主题(公式、定理)的起源、发现者或简史.
Slaught & Lennes (1915)在全书的18个主题之后加了历史注解:印度-阿拉伯数码的起源、运算符号的起源、括号(包括大、中、小括号)的起源、乘除法分配律的起源、“代数”一词的起源、用字母表示未知数、负数概念的发展、加法的结合律与交换律、乘法的结合律与交换律、指数、毕达哥拉斯定理、分数的书写方法、比与比例、字母系数方程与求根公式、用图形表示方程、根式、二次方程与虚根、二项式定理.
Young & Jackson (1913) 则在每一章的末尾给出历史注解,见表3.
与其他教科书不同,Cajori & Odell (1915; 1916)将有关数学史内容以整节的篇幅写入正文之中(但用了小号字),而非放在全书或某一章最后的附录之中.如“代数学的肇始”、“一元二次方程的历史”、“分数的历史”、运算律的历史、对数的发明等等.
关于代数学的早期历史(图7),Cajori & Odell介绍了古埃及人表达方程的方法,丢番图(Diophantus, 3世纪)、韦达、努内茨(P. Nunes, 1502—1578)表达幂的方法,雷科德等号“=”的发明.
关于运算律,Cajori & Odell告诉读者,尽管代数学的历史可以上溯到公元前2000年,但在19世纪以前,人们只是默认交换律、结合律和分配律是正确的,无人给出证明,19世纪法国、德国、美国有关数学家的工作才使代数学臻于完善.法国数学家赛尔瓦(F. J. Servois, 1768—1847)最早给出“交换律”和“分配律”之名 ;英国数学家哈密尔顿最早给出“结合律”之名.

表3 Young & Jackson (1913)中的历史注解
关于对数的历史,Cajori & Odell介绍了苏格兰数学家纳皮尔(J. Napier, 1550—1617)在发明对数之前的一段经历:纳皮尔曾长期住在恩德里克河畔一座风景秀丽的城堡里.城堡对岸有一家棉绒厂,厂里发出的噪音常常打断纳皮尔的思路,纳皮尔曾希望厂主关掉工厂.
2.7 数学概念
如果一个知识点发生发展的逻辑序和历史序有差异,那么教科书在编排该知识点时就需要在参照学生心理序的基础上,在两者之间作出适当的选择.Beman & Smith(1900)借鉴历史序来呈现数系扩充的过程,如图8所示.编者将零的引入安排在负数之后,也符合历史序.
2.8 思想方法
Slaught & Lennes (1915)在一元二次方程的解法中,除了通常的配方法,还采用了“印度配方法”:在方程ax2+bx+c=0两边乘以二次项系数4a,得
4a2x2+4abx=-4ac,
两边加上b2,得
4a2x2+4abx+b2=b2-4ac,
即
2ax+b2=b2-4ac.
这种配方法最早由11世纪印度数学家斯律陀罗(Siridara)给出,其优点是避开了分数的使用.

图7 Cajori & Odell (1915, 1916)所介绍的代数学早期历史
图8 负数的引入
3 讨论
3.1 数学史的运用方式
数学教科书运用数学史的方式可分为点缀式、附加式、复制式、顺应式和重构式五种(汪晓勤,2012).
点缀式是以“装饰”、“美化”、“人性化”为目的的运用方式.数学家的画像、古代数学书籍、数学符号、测量或作图工具的图片、反映数学主题的艺术作品等都属于点缀式素材.所考察的11种代数教科书中,出现最多的点缀式素材是数学家的画像.但点缀式素材并非仅仅为点缀而点缀,而是以图辅文、图文相配.如,Cajori & Odell (1915,1916)在介绍代数学历史时,介绍了韦达和笛卡儿表达方程的方式,故在不同章的末尾配上两位数学家画像,并在画像的下方给出各自的方程表达方式.一般地说,教科书使用的都是对所涉及学科或主题作出重大贡献的数学家的画像.
附加式是以“追溯历史起源、补充历史知识、提供辅助材料”为目的的运用方式,附加式素材通常以附录、注解的形式出现,可与正文内容分离.11种代数教科书中,名人名言、词源分析、数学家生平介绍、数学专题的历史注解均属于附加式素材.
复制式是指原原本本采用历史上的数学问题、问题解法、定理证法等,或直接在正文中介绍有关主题的历史.复制式数学史素材是教科书正文不可分割的一部分,其功能是提供数学问题、再现古人智慧、促进数学学习.在11种教科书中,采自数学史文献的问题和方法都属于复制式素材.
所谓顺应式,是指根据历史材料来编制问题,或将历史上的数学问题进行改编,使之更适合于今日的教学,或将历史上的思想方法进行改进、简化使之顺应时代.顺应式数学史素材也是教科书不可分割的一部分,其功能是提供数学问题、增加探究机会、展示数学思想、激发学习兴趣.尽管11种教科书采用了较多的数学史问题,但只有Schultze (1918)的开普勒行星定律的应用问题和完满数问题属于顺应式.
重构式是指借鉴知识的发生、发展历史,以发生法来呈现知识.重构并非原原本本的重复,而是在借鉴历史的基础上,结合知识的逻辑序和学生的心理序,自然而然地呈现一个主题,其功能是把握认知基础、激发学习动机、促进数学理解.Beman & Smith (1900)引入负数概念的方式即属于重构式.然而,这种方式在早期教科书中用得很少.
图9给出了11种教科书中的数学史素材类别与五种运用方式之间的对应关系.

图9 各类数学史素材在代数教科书中的不同运用方式
3.2 数学史素材的若干特点
早期代数教科书对数学史素材的运用,呈现出以下特点.
其一,不同教科书运用数学史的情况千差万别.
11种代数教科书或多或少都运用了数学史,但运用数学史的数量和方式不尽相同,并没有什么标准.若进一步考察同时代更多的代数教科书,则会发现:在很多教科书中几乎见不到任何数学史素材.显然,数学教科书中是否运用数学史、运用多少、如何运用,都取决于编写者对数学史的了解以及对数学史教育价值的认识.Beman & Smith(1900)、Young & Jackson(1913)、Cajori & Odell(1915)、Slaught & Lennes(1915)等运用数学史,成了那个时代的典范.
其二,数学教科书运用数学史的情况与同时代数学史学术研究状况密切相关.
史密斯、卡约黎都是专业数学史家,而贝曼、杨格(J. W. A. Young, 1865—1948)、斯劳特(H. E. Slaught, 1861—1937)等数学家对数学史也都有浓厚的兴趣,贝曼曾与史密斯合作翻译德国学者芬克(K. Fink, 1851—1898)的《初等数学史》(1899)和《数学简史》(1900),杨格在数学史方面也有著述.尽管如此,他们所掌握的数学史知识明显有着时代的局限性.例如,他们在教科书中只字未提中国古代数学家对负数的运用以及在二项式定理、一元高次方程、高次方程组、等差数列等方面的具有世界意义的工作.实际上,在英国著名科学史家李约瑟(J. Needham, 1900—1995)出版《中国的科学与文明》之前,西方学者对于中国古代数学成就知之甚少;甚至连M·克莱因(M. Kline, 1908—1992)这样学问宏博的数学史家也完全忽略中国古代数学的成就.
其三,数学课程改革对数学史在教科书中的运用产生重要影响.
20世纪初,培利运动如火如荼,科学人文主义运动方兴未艾,数学课程处在变革之中.由美国数学协会(史密斯、斯劳特先后担任过会长)成立、杨格担任会长的“全国数学需求委员会”试图对美国的数学课程进行重构,该委员会在报告建议,为了激发学生对数学的兴趣,揭示该学科的意义,必须在教学中广泛使用数学历史和传记材料(The National Committee of Mathematical Requirements, 1922).在这样的背景下,作为课程改革的引领者,斯劳特、杨格、史密斯等在教科书中注重数学史素材的运用,也就成为自然而然的事了.
4 结语
20世纪初的11种美国代数教科书使用了较为丰富的数学史素材,涉及名人名言、数学人物、数学名词、文献资料、数学问题、数学概念、思想方法、专题历史等,其中使用最多的是数学问题和专题历史;运用数学史的方式有点缀式、附加式、复制式、顺应式和重构式,但顺应式和重构式很少出现;教科书运用数学史的情况与同时代数学史研究、编写者的数学史素养以及当时的数学课程改革大背景息息相关.
数学史融入数学教科书,在今天仍是一个颇受关注的主题,早期教科书所用数学史素材的类别较为丰富,为我们带来了很多思想启迪.
其一,让数学人性化、富有趣味性和吸引力,是教科书运用数学史材料的重要目的之一,教师或教科书在介绍数学家生平时,可以按照“一个人物、一个故事、一个主题和一种思想”来展开;
其二,名人名言、数学术语的词源、专题的历史等附加式素材在今日教科书中并不多见,而这些素材都有助于学生对相关主题的学习,完全可用于今日教科书或课堂教学之中;
其三,历史上的数学问题或基于数学史编制的数学问题是最重要的复制式或顺应式素材,尽管近年来中考或高考试卷上出现了一些数学文化问题,但问题来源相对单一,基于数学史的问题编制理应成为未来数学教师重要的研究课题;
其四,兼顾历史序、逻辑序和心理序,是概念呈现或概念教学的指导思想,是否遵循这一指导思想,决定数学史运用水平的高下.
将数学史融入数学教科书是一项系统工程.编写者不仅需要对数学学科的育人价值以及数学史独特的教育价值有深刻的认识,而且需要掌握丰富的数学史素材和对数学史料进行裁剪和加工的策略.在20世纪之初浩如烟海的西方代数教科书中,只有极少数运用数学史,这一事实充分证明:对于教科书编写者而言,数学史的运用并非易事,而要做到历史序、逻辑序和心理序的统一,则更为艰难.我们有理由相信,教科书如何运用数学史素材、用什么数学史素材,是一个需要数学教育研究者和数学史研究者交流合作、长期研究的课题.

