第十一届高中数学水平能力测试M-A(高三)试卷
(考试时间120分钟,满分120分)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
A.[24,48] B.[24,48)
C.[48,96] D.[48,96)
【答案】D
(供题人:中国人民大学附属中学 王鼎)
A.(0,1) B.{1} C.[1,2) D.[1,2]
【答案】B
(供题人:北京中学 张欣然)

A.1 B.2 C.3 D.4
【答案】C
(供题人:北京四中 贾祥雪)
4.将有理数集Q划分成两个非空的子集M与N,满足:M∪N=Q,M∩N=∅,且M中的每一个元素都小于N中的每一个元素.给出以下四个结论:
①M没有最大元素,N有一个最小元素;
②M没有最大元素,N也没有最小元素;
③M有一个最大元素,N有一个最小元素;
④M有一个最大元素,N没有最小元素.
其中所有可能正确的结论的序号是________.
A.① ② ③ B.① ② ④
C.① ③ ④ D.② ③ ④
【答案】B
(供题人:首都师范大学附属中学 李洋)
5.设函数f(x)的定义域为D,若存在x0∈D,使得f(x0)=x0,则称x0是f(x)的不动点.函数f(x)=ex-x2的不动点的个数为________.
A.0 B.1 C.2 D.3
【答案】B
(供题人:北京昌平一中 刘克光)
6.线段AB,CD如图所示,假设曲线y=f(x)经过点B和C,且在B,C处的切线分别为直线AB和CD.给出以下三个论述:
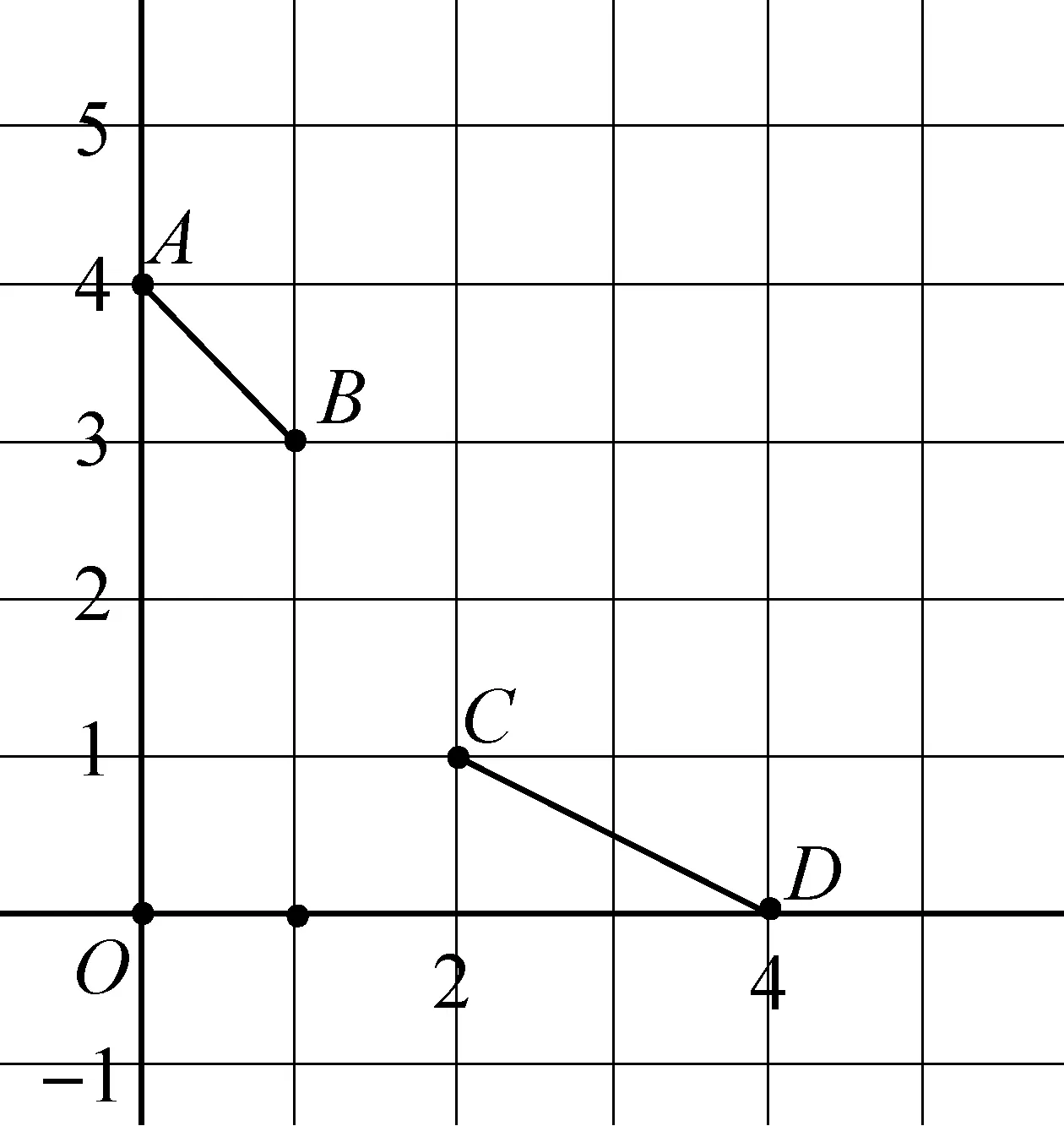
① 若f(x)=ax3+bx2+cx+d,则f(x)是唯一存在的;
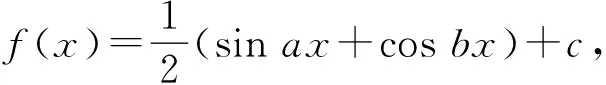
③ 若f(x)=ax4+bx3+cx2+dx+e,则f(x)是唯一存在的.
其中所有错误论述的序号是________.
A.① B.② C.③ D.② ③
【答案】D
(供题人:北京汇文中学 田会永)
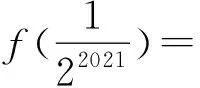
【答案】B
(供题人:北京大学附属中学 李静 单治超)
8.设(1+x+x2)1000=a0+a1x+a2x2+…+a2000x2000,则a0+a3+a6+…+a1998=________.
A.3333B.3666C.3999D.32000
【答案】C
(供题人:北京牛栏山一中 李金彪)
二、填空题:本题共8小题,每小题5分,共40分.

【答案】1
(供题人:北京四中 贾祥雪)
2.设[x]表示不超过x的最大整数.若实数a∈(0,1)满足:
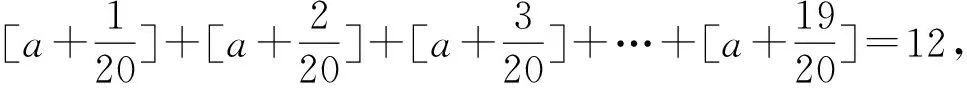
【答案】3
(供题人:北京工业大学附属中学 肖志军)

【答案】18
(供题人:北京陈经纶中学 孙丕训)
4.设点A与点B分别位于曲线y=ex与曲线y=lnx上,则线段AB的长度的最小值为.

(供题人:北京十一学校 潘国双)
5.如果圆x2+(y-1)2=r2与曲线(x-1)·y=1没有公共点,那么半径r的取值范围是.
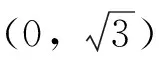
(供题人:北京工业大学附属中学 肖志军)
6.已知集合A=1,2,3,…,15.若集合B=xx=ab,a∈A,b∈A满足:∀x∈B,∃k∈N*,使得x=6k,则集合B中元素的个数最多为.
【答案】25
(供题人:北京清华大学附属中学 郎春雨)
7.如图,F1,F2是平面上的两点,且|F1F2|=10,图中的一系列圆是圆心分别为F1,F2的两组同心圆,每组同心圆的半径依次是1,2,3,…,点A,B,C分别是其中两圆的公共点.写出一个圆锥曲线的离心率的值,使得此圆锥曲线同时满足:① 以F1,F2为焦点;② 经过A,B,C中的两点.

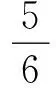
(供题人:北京八一中学 荣贺 曲艺)
8.对于正整数k,记f(k)表示k的最大奇因数,如f(3)=3,f(20)=5.设
Sn=f(1)+f(2)+f(3)+…+f(2n),
则S2021=.
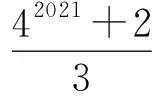
(供题人:北京牛栏山一中 李金彪)
三、双填空题:本题共4小题,每小题两空,每空5分,每小题10分,共40分.


(供题人:北京四中 贾祥雪)
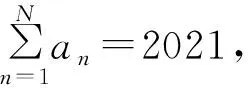
【答案】53,65
(供题人:北京陈经纶中学 孙丕训)
3.黑板上写着自然数1,2,3,…,2021,小明每次擦去两个奇偶性相同的数,再写上它们的平均数,最后黑板上只剩下一个自然数,则这个数可能的最大值为,可能的最小值为.
【答案】2020,2
(供题人:北京十一学校 潘国双)
4.用字母a,b,c组成字符串.长度为2的字符串中,不是由两个a组成的不同的字符串的个数为,长度为5的不同的字符串个数为.
【答案】8,164
(供题人:北京第十二中学 马超周)

