数学教学如何“立德树人”
石志群
(江苏省泰州市教研室 225300)
教育部于2014年发布了《教育部关于全面深化课程改革落实立德树人根本任务的意见 》,提出“立德树人”是教育的“根本任务”.学科教学是实现立德树人的主阵地,那么,数学学科如何“立德树人”呢?
1 数学的严谨性、逻辑性特征:“讲理”的德行,“守规”的习惯
俄国数学家A.D.亚历山大洛夫在《数学,它的内容、方法和意义》一书中这样表述数学学科的特征:“对数学只有肤浅的知识就能容易察觉到数学的这些特征:第一是它的抽象性,第二是精确性,或者更好地说是逻辑的严格性以及它的结论的确定性,最后是它的应用极端广泛.”,数学的严谨性表现在它的“讲理”,即作出任何结论都必须有理有据,这不仅对培养学生的严密的逻辑思维习惯非常有益,更能够使学生成为一个“讲理”的人;数学的公理化思想方法,以及基于公理化思想和逻辑推理的规范又能够让学生形成守公德、讲规范的行为习性.
当然,要实现数学教育的上述价值,在数学教学过程中就必须突出数学的“严谨”性特征,明确严格的逻辑要求.即使暂时还不宜进行严格证明的内容,也要让学生知晓,在数学中这些结论是一定要进行严格证明的,绝对不能以直觉代替逻辑、以特例代替一般.
一是要在教学中尽可能地严谨、严密,即使暂时还不能或不便进行逻辑证明的内容,最好也要向学生说明这个过程是不严密的,这种推理是合情推理,其结论的正确性并不能保证,因此,需要证明,当学习了相关知识后我们将可以进行严格的证明.比如,初中是用描点法研究一次函数、二次函数及反比例函数的,所有教材都由特殊的一次函数,用描点法画出图象,并直接下结论:一次函数的图象是直线;有些教材上在用描点法画出特殊的二次函数的图象后,直接指出:二次函数的图象是抛物线;甚至有些教材出现了反比例函数图象是双曲线的说法.其实,这个时候,学生对直线、抛物线及双曲线的定义都不了解(直线的概念是描述性的,本身就是元概念),所以,教学过程中应该向学生说明:这些结论将能够在以后的数学学习过程中给出证明.到了高中学习了解析几何相应内容后,最好能够将直线、圆锥曲线与一次函数、二次函数内容进行体系建构,说明:根据确定直线的条件(直线上的一个点和直线的方向)求得直线方程的过程,其实就是证明了初中所学习的内容:一次函数的图象是直线;学习了抛物线方程后,既可以用抛物线的定义证明二次函数的图象是抛物线,也可以通过标准方程对应的抛物线的“变换”证明二次函数的图象是抛物线;同样地,也可以用定义证明反比例函数的图象是双曲线.
二是要在教学中体现数学知识体系.比如,平面几何、立体几何的逻辑结构、三角恒等变换、基本不等式中的等式、不等式的逻辑关系,由此初步渗透公理化的思想方法.
三是做题时要按数学的书写规范严格要求,确保每一步过程都要符合逻辑规范.比如,复数除法运算部分的例题解答中运用“分母实数化”的方法时,要说明其理论依据是分数的性质在复数范围内仍然成立,以此保证运算过程的严谨性.教学中要让学生感受到建立理论依据的必要性和重要性.
当然,教数学的推理与逻辑要揭示“数学是生活常识的精微化”的特点,从数学到生活,引导学生做到:思考问题、发表观点要有理有据,符合逻辑;语言、行为要符合社会公德和法律法规,做一个讲道理、明事理、守规则的人.这正是数学学习健全人格之功能所在.
2 数学的理性精神:求真、求善、求美
真、善、美是德行的核心,也是“审美情怀”的内涵.恰好,数学的理性精神之根本就是求真、求善、求美.英国数学大师罗素认为“数学,如果正确地看待它,则有……至高无上的美——正像雕刻的美,那是一种冷峻的美.它没有绘画或音乐的华丽装饰,却纯净而崇高,可以达到伟大艺术的完美境界.”“一种真实的喜悦,一种精神的亢奋,一种超越人的意识——这些至善至美的标准,能在诗歌里得到,也能在数学中得到”.……
在数学中获得真、善、美的美好感受,这几乎是所有数学家的共同体验.那么,数学家们的这种感受也可以让学生在数学学习的过程中获得吗?如果大量刷人为编制的那些中考、高考题,估计是无法获得的.如果我们在数学教学过程中让学生真实地面对数学家们当初面对的情境,经历发现问题、提出问题、分析问题、解决问题的全过程,如果在教学过程中让学生多做些经典的数学问题,或者即使无法完全理解,也可以让学生欣赏一些与学习内容相关的经典数学问题,就可以让学生较为充分地感受到数学的真善美.

即使是数学的符号,也都蕴含着丰富的真、善、美的价值追求.比如,表示相等关系的“=”,用上下一样长的两条水平线来表示“数量一样”,既简洁又美观,意义也很直观,将数学的符号美表现得淋漓尽致.再比如,表示不等关系的“<”、“>”,其从近乎文字的符号形式发展到得到大家共同认可的现在的形式,经历了数百年的时间,即使现在的符号,从出现到普遍使用,也过了100多年.由哈里奥特创立的这种简洁优美的不等号,不管后人怎样去重新创造,都无法被取代.教学过程中遇到需要使用符号简化表示形式的时候,最好能够研究一下“用怎样的符号来表示呢?”并让学生从简洁、优美、形象的角度去构造,最后再简要地介绍一下数学中约定的符号的发展史,欣赏符号的美及蕴含其中的精神内蕴.
3 数学的观念、思想、方法:创新与创造(发现)
数学学科立德树人的价值还深刻体现在数学的观念、思想和方法中,甚至是由此获得的结论的奇异、美妙之中,体现在其巨大的创新、创造(发现)的功能上,而数学家们在观念、思想和方法的创新、创造的过程中表现出的科学精神,即理性思维、批判质疑、勇于探究的精神与品质也正是“立德树人”根本任务的重要内容.
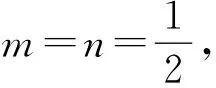
上述过程,既表现出了数学家们的“精神”:总是喜欢将特殊向一般“推广”,以创造出更一般的“数学”,从而扩展数学的应用价值,也在更广泛的层次上运用数学刻画自然,又体现了数学的价值观、审美观,即求统一、求简单、求和谐的价值追求与审美追求.这无疑会对学生的审美能力的提高、审美情趣的形成及由此生成的数学创新、创造力产生积极的作用.
二是通过向学生“打开一扇窗”,使感兴趣、有能力的学生能够欣赏到一流数学家们的数学观念、思想、方法.比如,可以介绍伟大数学家欧拉求
的完整过程,特别是在“问题解决”的过程中使
1=(1-a)+(a-a2)+(a2-a3)+(a3-a4)+ …,
并得到
等重要的变形转化过程中所体现的伟大的数学思想加以揭示,可以使学生感受一流数学家们的巨大创新能力的同时,体会到平时做数学题的那些所谓技巧应该融于问题解决过程的思维分析之中而产生,切不可只是一种套路.如果从立德树人的个性化特点看,要培养一流的数学家,必须向大师学习,学习他们在数学观念、思想和方法上的伟大创新、创造的精神.正如著名数学家贝尔特拉米所说:“学生应该及早地像数学大师那样去追求和进行大量的创造性思考活动,而不要让学校里那种无休止的练习把自己的头脑弄得僵化和贫乏.实际上,沉溺在许多无益的练习之中,正好是一种无意义劳动掩盖之下的懒惰,这样做除了使人消磨意志之外别无其他作用.在伟大的前辈面前去努力创造会使人坚强.”
4 数学的文化价值:人文底蕴与人文精神
爱因斯坦曾说:“一种没有相当发达的数学的文化是注定要衰落的,一个不掌握数学作为一种文化的民族也是注定要衰落的.”我国著名数学家齐民友先生在其著作《数学与文化》一书中也说道:“因为数学在人类理性思维活动中有一些特点,这些特点的形成离不开各个时代的总的文化背景,同时又是数学影响人类文化最突出之点.” “数学深刻地影响着人类的精神生活,可以概括为一句话,就是它大大地促进了人的思想解放,提高与丰富了人类的整个精神水平.从这个意义上讲,数学使人成为更完全、更丰富、更有力量的人.”
就本质而言,数学的文化价值主要体现为理性探索精神.从可能始于应用性需求的勾股定理优美的公式形式,到它的优美的证明方法(达数百种之多),再到无理数的发现,甚至到费马大定理,无数中外数学家在这条道路上进行着艰辛的探索,获得了丰硕的成果,并成为人类精神文化的重要组成部分.这种素材正是应该为数学教学所重视的.
从数学家们的文化习惯的角度设计问题链是进行数学文化教育的有效途径.比如,数学家们为什么会想到求
这个问题的?这就如指数概念推广的过程一样,这与数学家们的探索精神密切相关:古希腊时代及中国古代就有求数列和的需求和传统,比如,毕达哥拉斯学派的三角形数、四边形数、……,由贾宪三角所形成的若干数列和,中国古代的“堆垛术”解决高阶等差数列和、……都说明这个问题.
教学中我们可以这样进行渗透:研究了
1+2+3+4+…+n
之后提出问题:解决了这个问题后,你觉得还应该解决怎样的问题?如果学生能够提出与之相关的拓展性问题,就对其进行系统化整理;如果学生提不出问题,就用“欣赏”的方式“告诉”学生:当初,数学家们由此想到了下面的这些和式能否求出来呢?
12+22+33+42+…+n2;
13+23+33+43+…+n3;
……
……
这些都是有限项之和,你觉得数学家们还会提出哪些具有“无穷多个项”的式子的和呢?
……
经常地让学生真实地欣赏、感受数学家们的思维方式,了解数学家们在提出问题、解决问题过程中的真实思维过程,以及其包含的数学思想方法,对发展学生的数学素养、感悟数学家们创新思维中的文化基因,从而提升核心素养是大有裨益的.
当然,数学文化的精神体现更应该在正常内容的教学过程之中,因此,我们的课堂上从提出问题开始,就要遵循数学理性探索精神的原则.通过现实的、科学的或数学的大背景,运用数学的大观念提出本章研究的大问题,再通过解决问题的逻辑思维过程,以数学家研究问题的基本规范展开教学内容.对于每节的内容,也是遵循上述原则,通过提出问题链的形式分析问题和解决问题.
数学真理的相对性对学生发展辩证思维与形成辩证观念也是非常有益的,这又是数学文化系统中一道独特的风景,比如,欧氏几何与非欧几何都是数学的重要公理系统和理论体系,在各自的系统中它们是自洽的、正确的,这种几乎难以想象的现象,其教育意义也是巨大的.尽管教材正文中没有这部分内容,但在苏教版高中数学教材阅读材料“几何学的发展”中系统简介了几何学的历史过程,这样的设计就是基于将数学文化作为数学教育的重要内容和形式,有机地融合、整合进教材,以实现立德树人的根本目标.
以上讨论了如何在数学学科教学中实现立德树人根本任务的一些思考,还很不全面,比如,数学具有应用的广泛性的基本特征,这种特征对于立德树人同样具有非常重要的作用,在教材中大量案例都体现着数学的这一特征:既体现了数学可以源自现实世界,又体现了数学模型在解决自然世界、社会生活中各种问题的重要作用,还便于使用具有德育意义的现实素材;数学家们的爱国敬业、献身科学、诲人不倦的事迹也是进行品德教育的好素材;……限于篇幅,就不赘述了.

