模式识别 美在其中

刘志昂

(苏州高新区第五初级中学校 215151)

人们对于美的追求是对于生命本真的追求，数学美是数学生命力的重要支柱，是数学教育目标之一，是数学教师对数学教学的理性追求．学校的数学教育教学，承载着美育教育的任务．

1 数学之美

美是自然的，是一切事物生存和发展的本质特征．法国数学家笛卡尔也说过，美是客观适应满足于主观感受与体验的一种特征．张文俊认为，数学的美就是数学问题的结论或解决问题过程适应人类的心理需要而产生的一种满足感，简洁的表现形式，精细的思考方法，处处充满着理性、高雅、和谐之美，这是真与善的客观表现[1]．

徐利治也指出，对于数学美的追求，归根到底还是对于数学真理的追求．数学乃是真与美的完整统一，尽管真与美的表现形式不尽相同，但在本质上却是一致的[2]．

数学之美有很多，如数学的统一之美、简洁之美、对称之美、奇异之美、结论之美、方法之美、结构之美等等．它们激发着人们心灵上的美感和灵感，使之迸发出创造性的思想火花．我们日常的数学教学，就需要培养学生发现数学之美和欣赏数学之美的能力，而模式识别这一解题教学策略就不失为一种非常好的方法．

2 模式识别

喻平认为，数学模式是指形式化地采用数学语言，概括地或近似地表述某种事物系统的特征或数量关系的一种数学结构．在数学问题解决中，具有共同结构的一类问题或具有相同解法的一类问题也称为一种模式．所谓模式识别，是当主体接触到数学问题之后，能将该问题归类，使得与自己认知结构中的某种数学模式相匹配的过程[3]．

罗增儒认为，在数学问题的解决过程中，所积累的知识和经验经过加工，会得出有长久保存价值或基本重要性的经典结构与重要类型——模式，将其有意识地记忆下来．当遇到一个新问题时，我们联想起已经解决的问题，在记忆中提取相应的方法加以解决[4]．

在几何解题教学中，模式识别是基本图形(或基本问题)的基本结论，基本思想和基本方法．往往通过对基本图形(或基本问题)进行各种变式，在解决问题的过程中，探寻出基本图形(或基本问题)及诸多变式的共同特征，概括出它们的一般规律，总结出基本图形(或基本问题)的基本结论，归纳出一般的数学思想和方法，构建出解决问题的模式．运用迁移、化归等数学思想方法，进行直接识别应用、间接识别应用、转化识别应用、变式识别应用、迁移识别应用、拓展识别应用，最终达到问题解决的目的．

图1

3 模式识别实践

下面以“正方形中的互垂线段”一例对如上的模式构建和识别应用加以解释．

3.1 从变式到模式

如图2，正方形ABCD中，点E，F分别在BC，CD上，且BE=CF．连接AE，BF交于点H．你可以得到哪些结论？你是怎样得到的？(△ABE≌△BCF，AE=BF，AE⊥BF，S△ABH=S四边形CEHF等，通过“SAS”证明△ABE≌△BCF即可以直接或者间接得到如上结论．)

设计说明这是一个结论开放的问题，鼓励学生猜想和验证自己得到的结论，最后引导学生分析所有结论的共性——都是通过△ABE≌△BCF得到的， 因而证明三角形全等是根本性的方法和结论．

变式1：将部分结论与题设交换，你可以得到什么命题？是真命题吗？如何证明？(若AE=BF或AE⊥BF或S△ABH=S四边形CEHF，均可得到如上的其它结论，且都是通过证明△ABE≌△BCF而直接或者间接得到)

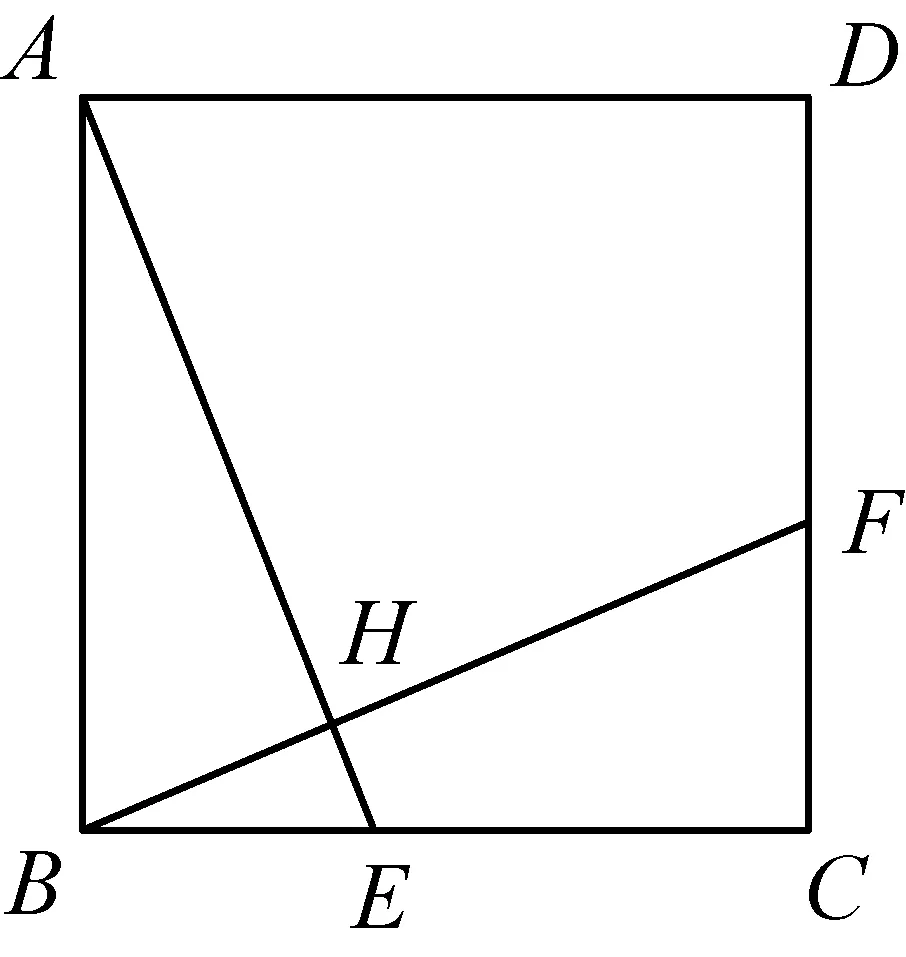
图2

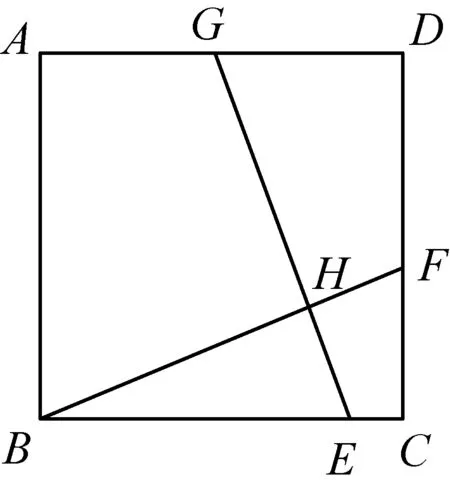
图3

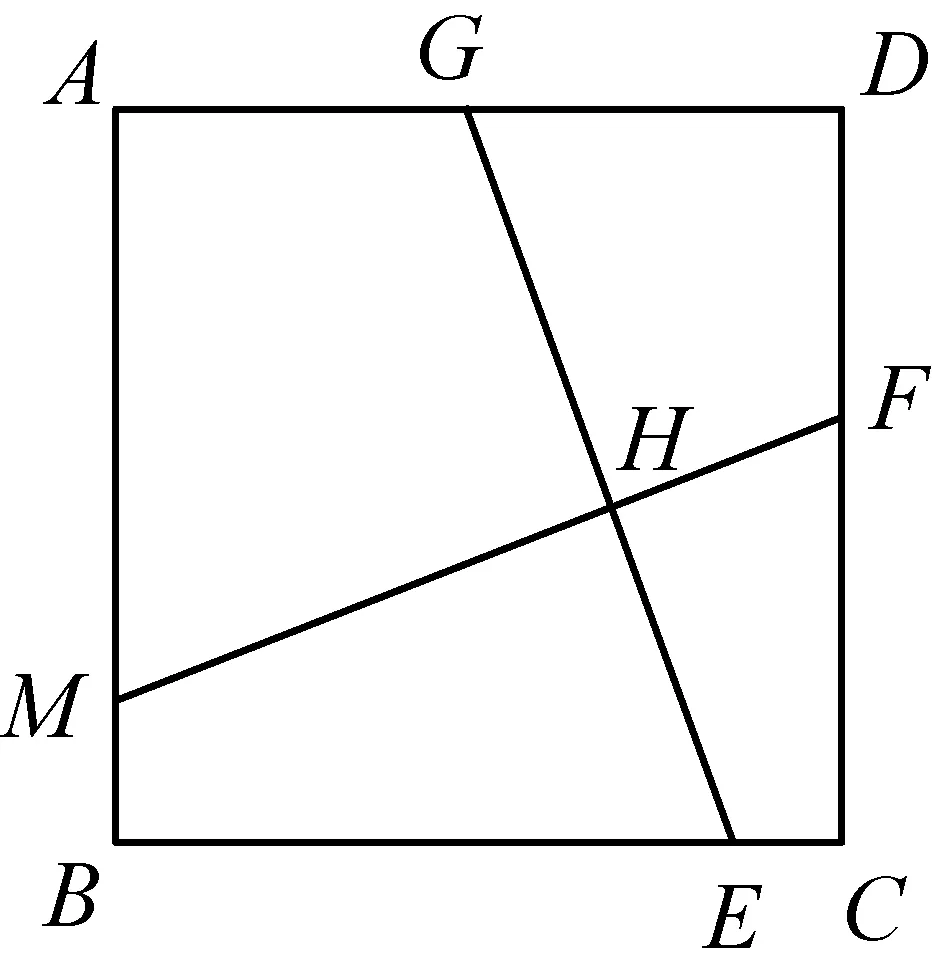
图4

变式2：如图3，正方形ABCD中，点E，F，G在边BC，CD，AD上，连接BF，EG交于点H．

(1)若BF与EG垂直，则BF与EG相等吗？你是怎样得到的？(若BF与EG垂直，则BF=EG，将GE向左平移，使G与A重合，证明所得三角形与△BCF全等即可)

(2)若BF与EG相等，则BF与EG垂直吗？你是怎样得到的？(在如图的情况下，同上平移构造全等是可以的；但是存在着其它情况：如果G的位置不变，E点靠近B点，也会有BF与EG相等的时候，此时BF与EG不垂直)

变式3：如图4，正方形ABCD中，点E，F，G，M在边BC，CD，AD和AB上，连接MF，EG交于点H．

你能提出什么问题吗？如何解决？(若MF与EG垂直，则MF与EG相等．将GE向左平移，使G与A重合；将MF向下平移，使M与B重合．结论同变式2．)

设计说明变式1是命题的互逆变式，变式2和变式3则是正方形的形内变式．通过变式让学生逐渐得到这样的结论：在这个特定的结构中，MF与EG若垂直则相等．都是通过平行化归构造全等三角形来得到的．

变式4：如图5，如果点G，E分别在AD，BC的延长线上，点F在CD上，BF的延长线交GE于点M．上述结论是否存在？如何说明？(若BF与EG垂直，则BF与EG相等是成立的，依然是通过平行化归证全等来得到的)

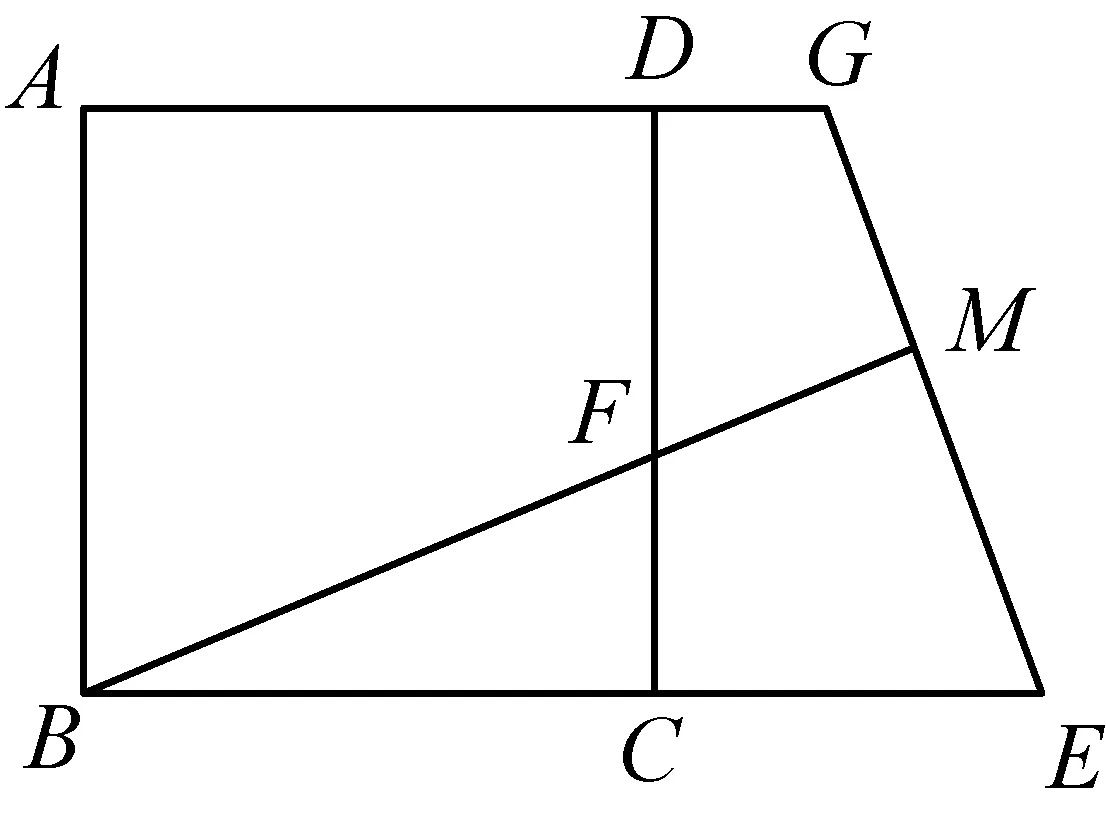
图5

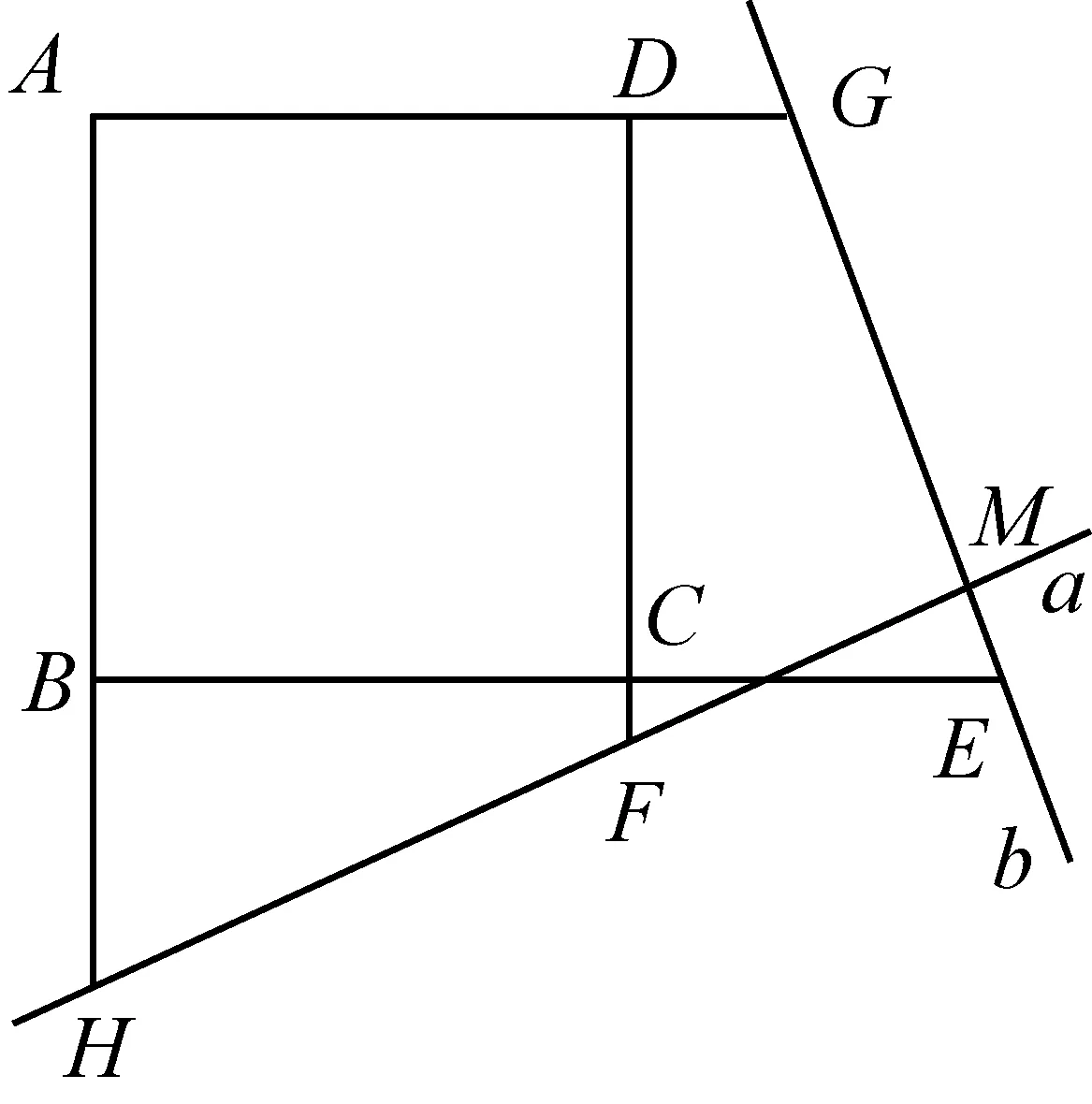
图6

变式5：如图6，如果直线a⊥b，垂足为M，直线a与AB，DC的延长线分别交于点H，F，直线b与AD，BC的延长线分别相交于点G，E． 上述结论是否存在？如何说明？(若HF与GM垂直，则HF与GM相等是成立的，依然是通过平行化归证全等来得到的)

设计说明变式4与变式5是在正方形的形外变式． 得到的结论与前面的变式一样，在这个特定的结构中，MF与EG若垂直则相等．这也是一个“变化中的不变性”：线段的位置在变，但是特殊的位置关系(互相垂直)没有变，特殊的数量关系(相等)没有变，证明的方法没有变：都是通过平行化归构造全等三角形来得到的．

在上面解决问题的过程中，我们构建出一个“模式”——即“基本图形的基本结论，基本思想和基本方法”．基本图形——端点分别在正方形两组对边所在直线上且互相垂直的两条线段．基本结论——这两条线段相等．基本思想——通过平行化归得到图2的基本图形．证明这一结论的基本方法——通过借助正方形的边和直角构造出全等的直角三角形，再运用全等三角形的性质来证明．

3.2 从识别到应用

例1如图7，E、F分别是正方形ABCD的边BC、CD上的点，AE、BF相交于点H，且AE⊥BF．下列结论：①AE=BF；②S△AHB=S四边形CEHF；③AH=HF．其中正确的有(填写序号)．

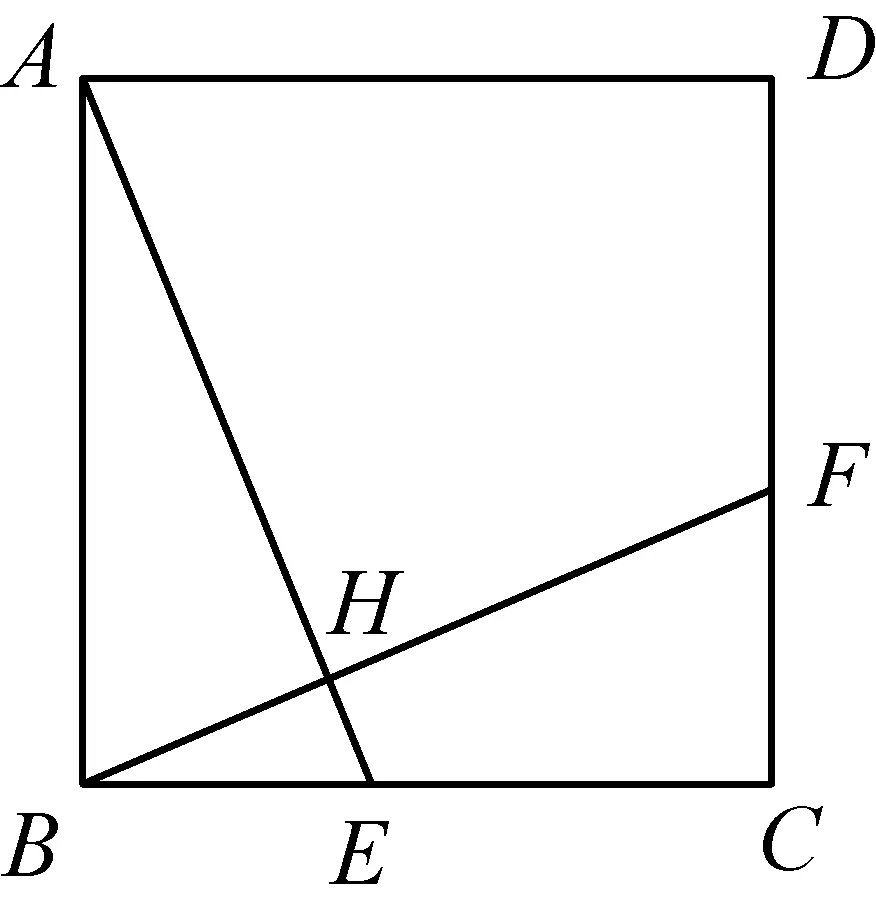
图7

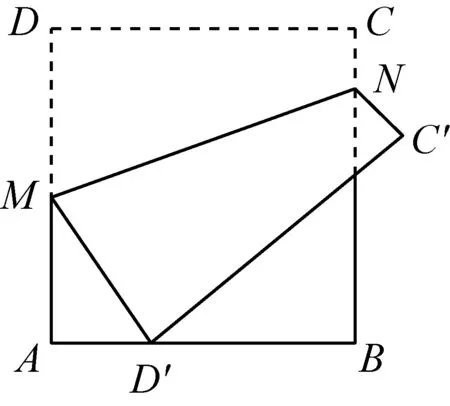
图8

设计说明这里可以直接识别出该图形就是模式中的基本图形，可以直接得出结论AE=BF，再通过证明三角形全等就可以对另外两个问题的正确性做出判断．

例2如图8，将正方形纸片ABCD沿MN折叠，使点D落在边AB上，对应点为D′，点C落在C′处．若AB=6，AD′=2，折痕MN的长为．

设计说明连接DD′．根据轴对称的性质得到DD′⊥MN，间接地识别出正方形中的互垂模式，通过三角形全等的证明得到DD′=MN，再运用勾股定理求出DD′的值即可解决问题．

例3已知，四边形ABCD是正方形，点P在直线BC上，点G在直线AD上(P、G不与正方形顶点重合，且在CD的同侧)，PD=PG，DF⊥PG于点H，交直线AB于点F，将线段PG绕点P逆时针旋转90°得到线段PE，连接EF．

①如图9，当点P与点G分别在线段BC与线段AD上时，请说明线段DP与EF有什么样的关系？

②如图10，当点P与点G分别在线段BC与线段AD的延长线上时，请猜想四边形PEFD是怎样的特殊四边形，并证明你的猜想．

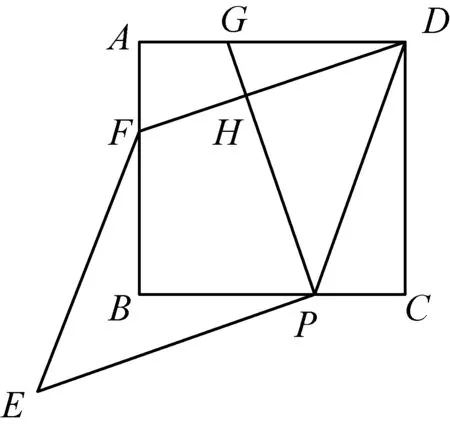
图9

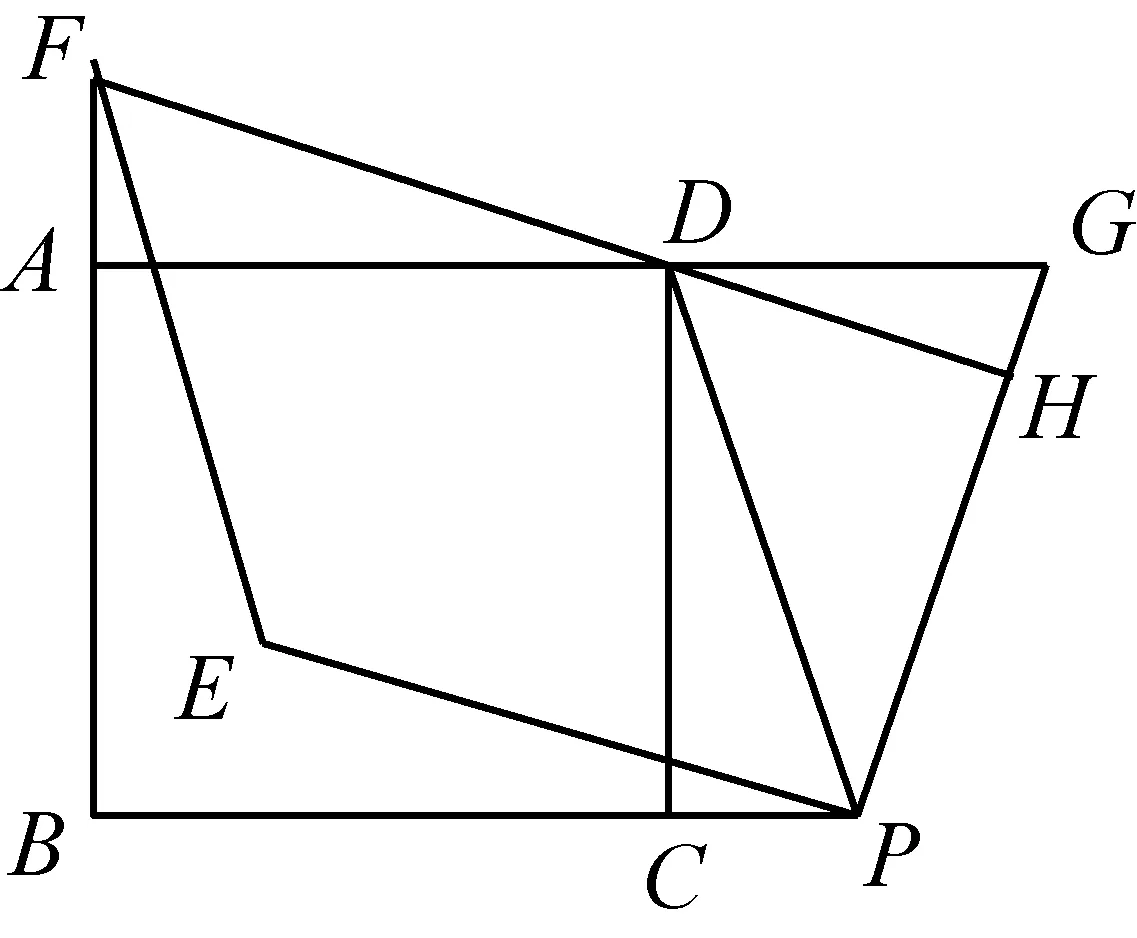
图10

设计说明①DP=EF且DP∥EF． 由点P在直线BC上，点G在直线AD上且DF⊥PG，可以识别出是图3中的正方形互垂线段模式，因而通过平行化归证全等后，结合图形旋转的性质得到PE=PG=DF，再证明PE∥DF．转化为证明四边形PEFD是平行四边形，因而DP=EF且DP∥EF． ②中点P与点G分别在线段BC与线段AD的延长线上，且DF⊥PG可以识别出是图6中的正方形互垂模式，同①证明出四边形PEFD是平行四边形，结合PD=PG=DF，所以PEFD是菱形．

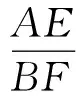
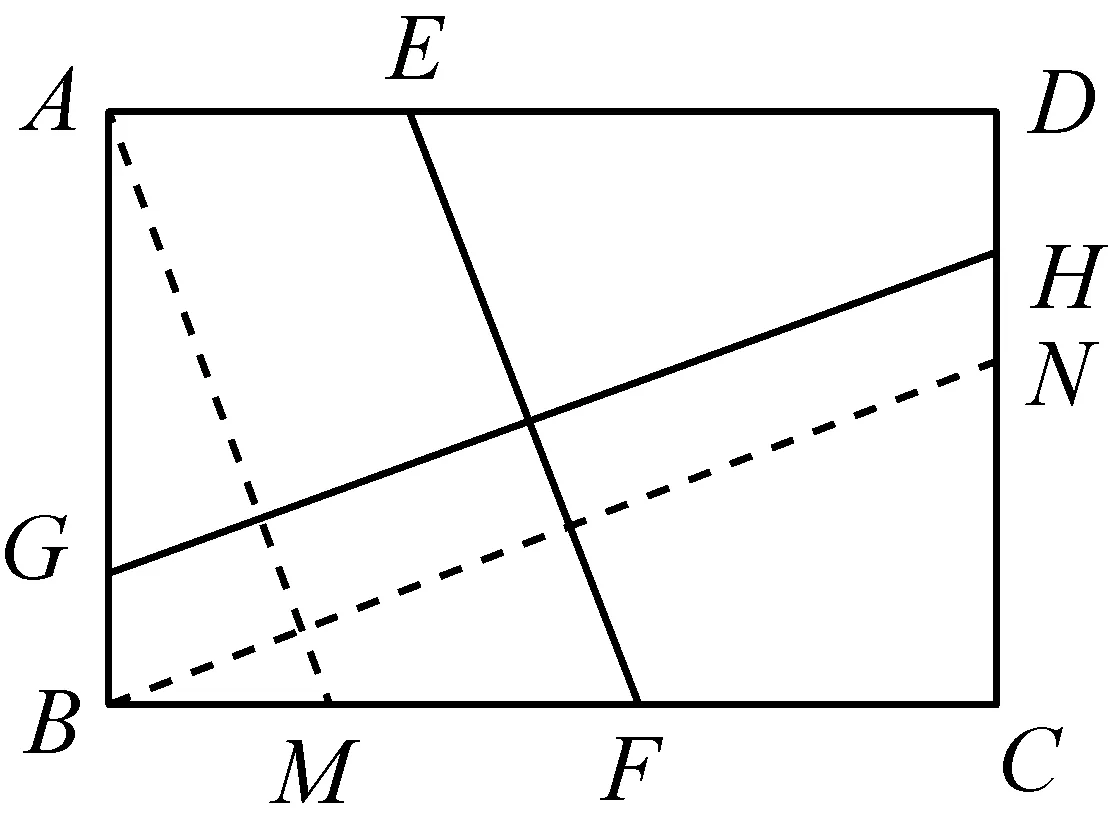
图11

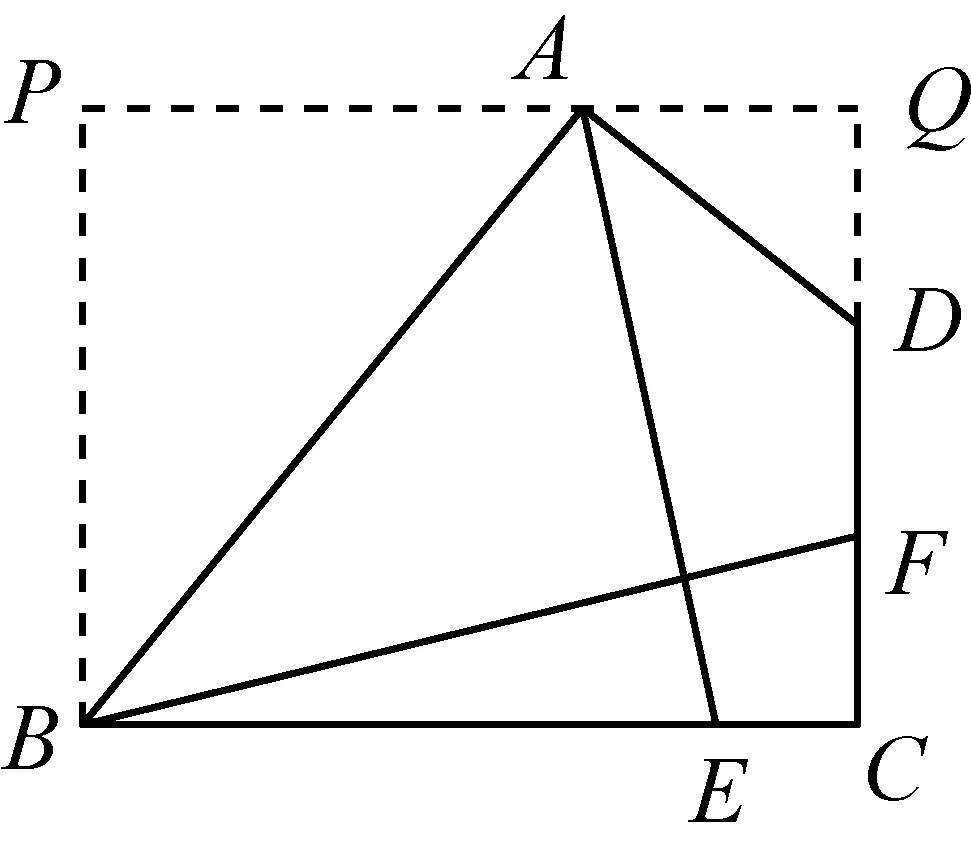
图11

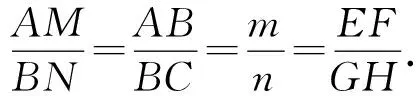
4 模式识别的数学之美

好而有用的模式总是具有模式美．所谓模式美就是模式本身表现出来的结构形式的和谐性和应用上的普适性．同时模式本身结论的简洁性、构思的精巧性，模式在构建过程中思维的和谐、方法的美妙也是与生俱来的，从模式的构建到模式的识别与应用，最终达成数学问题的解决，也形成了一个独特的数学学习结构．所以，模式识别具有简洁之美、结论之美、方法之美、结构之美．

4.1 简洁之美

数学的简洁美是数学之美的重要标志，它是指数学的证明方法、表达形式和理论体系结构的简单性，逻辑表述上的简洁性，主要包括符号美、抽象美、统一美、常数美等．

模式的构建，往往是在基本图形(或基本问题)的诸多变式中，建立它们之间的联系，找到其共同点，概括出共同的规律和根本属性，寻求变化中的永恒，动态中的静止，用不变规律来描述数学本质．模式的识别和应用，是一个从一般到特殊的过程，把一个个特例与构建的模式进行数学本质的比较，把复杂的问题化归为已经解决的问题，将数学问题的解决归结到自己熟悉的领域中．这就是模式识别的抽象美、统一美和常数美．

在上例模式的构建中，正方形中互垂线段(基本图形)的各种变式，通过平行化归证全等概括出一般的结论：端点分别在正方形两组对边所在直线上且互相垂直的两条线段相等．这个从特殊到一般的过程，是一个数学抽象的过程．在模式的识别与应用时，图形中识别出正方形的互垂线段(基本图形)的基本结论：若垂直则相等．而其中蕴含的基本思想和基本方法(平行化归证全等)是不变的，这既是抽象美，统一美，也是常数美，而“若垂直则相等”作为此模式的代名词，则为符号美．

4.2 结论之美

数学的结论之美主要表现在两个方面：形式美与内涵美．从形式上看，数学结论简洁、有序、对称、和谐等；从内涵上看，主要是结论自身的深刻性，比如揭示本质，建立联系，统一对象等，具有完备性和统一性[5]．

在上例模式的构建过程中，一系列的基本图形的变式(互逆变式、形内变式和形外变式)，是一个将特殊图形逐渐一般化的过程，构思是精巧而有序的；各种变式图形均可以通过平行移动而化归为基本图形，再通过证明三角形的全等来解决问题，它又是对称的、和谐的．上例中构造的模式“端点分别在正方形两组对边所在直线上且互相垂直的两条线段相等”本质上是一个数学命题，是一个正方形中两条特殊位置线段之间的特殊的数量关系，是一个由线段特殊位置关系向特殊数量关系转化的结论．显然是建立了联系，统一了对象，所以具有完备性和统一性，因而具有数学的结论之美．

4.3 方法之美

弗赖登塔尔认为：没有一种数学的思想，以它被发现时的那个样子公开发表出来．一个问题被解决后，相应的发展为一种形式化技巧，结果把求解过程丢在一边，使得火热的发明变成冰冷的美丽[6]．模式在构建过程中思维的和谐、方法的美妙也是与生俱来的，从模式的构建到模式的识别与应用，最终达到数学问题的解决，既是一个学习的过程，也是一个学习的方法．

在上例的模式构建过程中，各种变式中问题的解答，均是联想到基本图形中知识之间关联、问题解决的方法(通过全等三角形来解决问题)，而每种变式与基本图形之间也是有着内在关联的．接下来通过平行化归构造全等，将要解决的问题化归为已经解决的基本问题，本身就是一个“变更问题”[7]的方法，使问题的初始状态与目标状态愈来愈近．而模式的识别与应用，如上例中的直接识别应用、间接识别应用、转化识别应用、变式识别应用等，就是一个解题思路的产生与应用的方法，是一个数学思维方式获得的方法，还是一个用数学的方法，最终是一个数学问题解决的方法．

4.4 结构之美

模式是以抽象形式反映关系结构的，模式的识别与应用则是对这种关系结构的识别和应用的过程，因而模式识别既是一个数学抽象的过程，也是一个数学建模的过程．如上例就是从基本图形的基本结论出发，通过一系列的变式，引导学生归纳出诸多例证的共同特征，抽象出一般的规律，得到一般的结论，这是一个从特殊到一般的过程；而在诸多的识别与应用中，则是一个从一般到特殊的过程．

在上述的模式构建与识别、应用中，学生体会到不同的数学知识之间的内在关联，如正方形的性质、全等三角形的判定与性质、相似三角形的判定与性质、线段的特殊位置关系与特殊数量关系、平行四边形的判定与性质等等，形成了一个特定的知识结构．

学生通过对模式的构建与理解、模式的识别与应用，进一步地理解上述的知识，内化后将它们转化为自己的东西，变为内在的认知结构，这里“基本图形——端点分别在正方形两组对边所在直线上且互相垂直的两条线段．基本结论——这两条线段相等．基本思想——通过平行化归得到图2的基本图形．证明这一结论的基本方法——通过借助正方形的边和直角构造出全等的直角三角形，再运用全等三角形的性质来证明”就是一个特定的认知结构．

这一结构有助于学生的学习，有助于学生解决具有相关特征的数学问题，以达到问题解决的目的，因而形成了一个有效的学习结构．一旦形成这样的学习结构，学生在快速准确解决问题的同时，获得成功体验，有了快乐感受，产生积极情绪．这种积极情绪使得学生学习数学和愉快情绪建立稳定的联系，激发学生对数学学习的兴趣，促进学生学好的愿望和信心．法国数学家笛卡尔说过：“一般的说，所谓美和愉快，所指的不过是我们的判断和对象之间的一种关系．凡是能使大多数人感到愉快的东西就可以说是最美的．”