借助现代信息技术促进几何概念教学——以《5.1矩形》一课为例

孟泽琪

（杭州市勇进实验学校 浙江·杭州 310008）

1 问题的提出

我国《义务教育数学课程标准（2011年版）》在课程基本理念指出：“……数学课程的设计与实施应根据实际情况合理地运用现代信息技术，要注意信息技术与课程内容的整合，注重实效。要充分考虑信息技术对数学学习内容和方式的影响，开发向学生提供丰富的学习资源，把现代信息技术作为把现代技术作为学生学习和解决问题的强有力工具，致力于改变学生的学习方式，使学生乐意并有更多的精力投入到现实的探索性的数学活动中。

2 教学支持条件分析

利用几何画板制作课件，演示动态图形；截止希沃助手手机拍照上传投屏，随时拍照展示学生学习成果、及时呈现课堂细节；结合电子白板，学生触摸白板拖动图形，使课堂更加生动形象。

3 几何画板在《5.1矩形》的技术应用

3.1 课堂引入——开放式

问题1：如图1，用6根牙签棒首尾相接摆成一个平行四边形，思考：

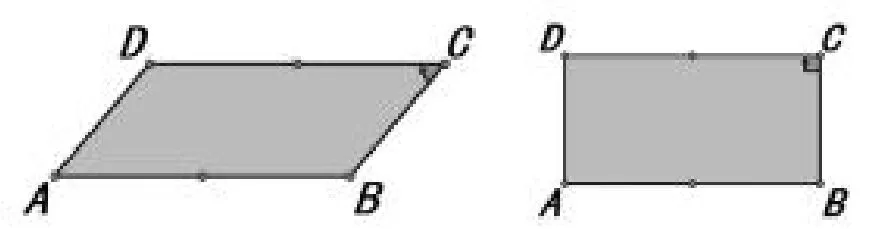
图1：平行四边形火柴和矩形火柴

（1）一共能摆成_________个不同的平行四边形？

（2）在这些平行四边形中，有没有面积最大的一个平行四边形？如果有请画出图形，如果没有请说明理由。

呈现两个问题后，演示平行四边形与矩形的动态变化,引导学生观察其垂线、对角线以及角度的变化，帮助学生从多角度分析图形的性质，如图1，学会从“边、角、对角线”来分析几何问题。引导学生学会理解矩形概念。

学生先行：通过收集学生的任务单发现，70%学生都能画出两种变形，其中就包括矩形类型，10%只画出一种，20%画出了多种变形，联想到平行四边形可以通过旋转得到矩形。

3.2 合作学习——探索式

教师提供几何画板的平行四边形模型，大胆放手让学生旋转、平移平行四边形，如通过点击几何画板中的角度摁钮，观察平行四边形某一角的角度变化；通过点击对角线摁钮观察平行四边形对角线长度的变化；通过点击垂线摁钮观察平行四边形高的变化。

问题2：尝试探索一下问题：

（1）平行四边形牙签的面积如何计算？

（2）过C点作高怎么画？

（3）这个直角在平行四边形的内部还是外部？

图2

【教学说明】问题 2中第（1）、（2）、（3）问引导学生想象平行四边形上的高，作高与底边，以及平行四边形内角角度有关，从高线的角度出发理解平行四边形与矩形不同点。

问题3：请根据平行四边形的动态变化，回答以下问题：

（1）当平行四边形变成矩形的时候，高怎么消失了？

（2）平行四边形的对角线有什么数量关系？

学生先行：学生们已观察到∠ABC变成直角的时候这个图形就是矩形。

在问题 3 中的第（1）、（2）中，在动态演示的过程中，可以得知，矩形具有平行四边形的所有性质，同时50%的学生反映高度的变化，知道高和边BC重合时就是这个图形面积最大的时候，学生细心的观察和提问，体现了在几何画板运用环境中，学生主动思考、操作、验证的能力，激发了他们的想象热情，说明几何画板可以提高整个课堂的上课效率，吸引学生眼球的同时，激发了他们的思考热情。

学生要想回答第（2）问需要运用类比，已知所有的平行四边形的对角线都是互相平分的，但不是所有的对角线都是相等的，当且仅当这个平行四边形是矩形时，才有可能使得这个图形的对角线相等，由此可以进入下一个环节：如何证明矩形的对角线相等。

【教学说明】在几何画板的动态演示中，分析矩形与平行四边形的异同点，感受图形的边、角、线之间的变化及联系，能建立起学习材料与学习者认知结构中已有知识的关系，产生有意义的学习。

问题4：根据平行四边形火柴的动态图像回答以下两个问题：

（1）面积最大的平行四边形出现在什么时候？

（2）一个角是直角的平行四边形是什么图形？

学生先行：当问及是否有面积最大的一个图形的时候，学生会有多种多样的回答，如90度角，对角线相等、高与BC边重合等，矩形是有一个角是90度的平行四边形。

【教学说明】学生在组合火柴的过程中，矩形的概念逐渐清晰，因为通过问题2让学生能够从多角度、多方向思考问题的核心，为学生自主选择学习内容提供了机会，问题激发了学生的数学想象能力和自信心。

3.3 概念类比——归纳式

在矩形概念形成的过程中，为了更加深入的理解矩形与平行四边形的关系，可以加入动画演示，从（1）定义（2）性质（边、角、线）（3）判定（用什么方法来证明这个图形？）三个角度动态展示从平行四边形到矩形的变化过程，可以加深学生对矩形本质的认识，即矩形是特殊的平行四边形。

同时，由于学生已学习平行四边形的概念，教师也可以从“边—角—线”等角度对矩形进行归纳，提升对矩形的认识。

【教学说明】通过直观的动态演示，有助于学生对矩形性质的理解，类比出概念学习的一般方法，其实理解图形性质还可以从边上的邻边、对边分析；也可以从角度上的邻角、对角分析；还可以从对角线是否平分、相等来分析；甚至可以从对称性来分析，至于如何证明这些关系，可以留给学生更多的想象空间去课外思考了。

4 信息技术辅助几何概念教学的几点反思

4.1 信息技术拉近生活与数学之间的距离

在初中教学中，教师往往都是直接通过PPT动画来完成几何图形的概念理解、习题分析。而几何画板往往通过画图和动画演示等形式，将某些抽象的概念转化为直观的图像，有助于学生理解几何概念。

在帮助学生学习方面，几何画板在结合现代电子白板的交互界面上，学生直接可以用手操作投影画面，课堂中所有学生都可以直观、近距离的观察、操作、演示，不仅可以深深吸引学生的眼球，并且通过长期的使用和讲解，学生在处理数学问题时，会联想到用信息技术来解决数学问题，促使学生运用信息技术来解决问题。

同时，教师也需要保证学生能充分体验数学情境。本节课在摆放牙签（五分钟）一位学生利用几何画板在电子白板上摆放牙签，其他学生在学习单上画出草稿、探索矩形的“边角线”（10分钟），如：学生在电子白板上随意拖动、旋转平行四边形观察图形变成矩形的过程中的变化，得出自己的数学猜想；了解矩形的对称性（5分钟），如：学生通过拖动矩形观察矩形在放大缩小过程中的对称性，这些环节都给学生留有足够的时间（5分钟+10分钟+5分钟=20分钟），学生不仅对信息技术展现数学原理非常感兴趣，学生对自主探究出来的概念和结论也是记忆犹新，在这样的操作、展示的过程中，教师发现，学生对几何画板的操作、功能都有了新的认识和兴趣，他们更愿意去了解和学习新技术的更多功能，提高参与、讨论数学问题的激情，培养重新创造数学的能力。

4.2 利用信息技术体验类比思想

本节课使用几何画板，从点、线、面三个角度（或者说是边、角、线）动态演示了平行四边形变成矩形的具体过程，尤其是动态演示过C点作直线AB的高，当高与边BC重合的时候，使学生联想到有一个是90度的平行四边形是矩形。

5 结束语

在一般教学情况下，学生会忽视矩形对角线的特征，但通过几何画板演示发现，矩形的对角线是相等的，这些都是信息技术所带来的生长点。本节课从观察、思考、证明三个步骤充分培养了学生自我探索、类比论证的能力，提供了学生展示自我的平台，使用信息技术当堂演示、互动、展示，增强了课堂的可操作性，加强了学生对几何概念的理解。