Frobenius扩张下的W⊥-Gorenstein内射性

宋 维

(浙江机电职业技术学院 数学教研室, 浙江 杭州 310053)

文中的环R,S均指带有单位元的环,若非特别指出,R-模均指右R-模,Mod-R表示所有右R-模构成的模范畴,idR(M)表示MR的内射维数,r.gldimR表示环R的右整体维数.

倾斜理论是代数表示论中的最基本也是最重要的内容之一,其最本质的研究对象就是倾斜模以及由倾斜模诱导出的一些子模范畴之间的对应.广义倾斜模(也称Wakamastu倾斜模[1])首先由Wakamastu[2]提出广义倾斜模(也称Wakamastu倾斜模[1]).一方面,广义倾斜模具有很多和倾斜模类似的性质；另一方面,一个和广义倾斜模相关的Artin代数表示论中的著名的同调猜想,称之为Wakamastu倾斜猜想(WTC),与表示论中其他著名猜想密切相关.例如,可以利用著名的有限维猜想推出Wakamastu倾斜猜想,利用Wakamastu倾斜猜想可以推出Gorenstein对称猜想和广义Nakayama猜想等[1,3-4].

目前,关于Gorenstein同调代数的研究已有许多结果.作为Gorenstein内射模的推广形式,Ouaighi[5]定义了X-Gorenstein内射模类,这里的X指的是包含内射模类的一个模类.这种模类统一了一些重要的同调模类,事实上,若令X为所有内射模的类,则X-Gorenstein内射模即为经典的Gorenstein内射模.Meng等[6]给出这类模许多重要的性质.

环扩张理论中,一类重要的环扩张为Frobenius扩张,它是Frobenius代数的一种推广,它在代数表示论、结构理论以及拓扑量子域理论中均有重要作用[7-10].Frobenius扩张的研究通常会和可分扩张联系在一起,即是可分的Frobenius扩张,其基本的例子是群代数在其具有有限指数的子群代数上的扩张,更多的例子可参见文[11,例2.4].

1 W⊥-Gorenstein内射模

首先回顾广义倾斜模的概念.

定义1一个有限生成的R-模WR称为一个广义倾斜模(或称为Wakamastu倾斜模[1]),若WR是自正交的,即对任意的i≥1,均有

且存在正合列

使得

1) 对i≥0,每个Ti∈addWR,这里的addWR指的是由所有的同构于WR的有限直和的直和项构成的R-模的全子模范畴.

2) 用HomR(-,WR)作用上述正合列后仍是正合的.

回忆一个R-模类是一个内射预解类,指的是它包含内射模类,并且对扩张和单同态的余核封闭.对于一个广义倾斜R-模WR,定义

对于一个广义的倾斜模W,在Gorenstein内射模定义[14]的基础上,定义W⊥-Gorenstein内射模如下:

定义2设WR是一个广义倾斜模,一个R-模MR称为W⊥-Gorenstein内射指的是存在内射模的正合列

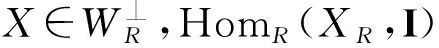
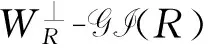
根据上述定义,容易得到关于W⊥-Gorenstein内射模的一些基本事实:

1) 每个内射R-模是W⊥-Gorenstein内射的.

2) 每个W⊥-Gorenstein内射模是Gorenstein内射的.

3)W⊥-Gorenstein内射模是一个内射预解类,且对直积和直和项是封闭的(见文[6]命题2.10).

下面的引理是对文[14]中引理3.12对偶结论的一个应用.

引理1设MR是一个R-模,考虑下面的两个正合列

2 Frobenius扩张下的W⊥-Gorenstein

内射性

1)T=-⊗RSS:Mod-R→Mod-S是由MR→M⊗RSS给出.

2)H=HomR(SSR,-):Mod-R→Mod-S是由MR→HomR(SSR,MR)给出.

容易验证(T,F),(F,H)均是伴随对.

由文[8]中的定义1.1和定理1.2得Frobenius扩张.

定义3[8]一个环扩张S/R称之为Frobenius扩张,指的是它满足下列等价条件:

1) 函子T和H是自然等价的.

2)RSS≅HomR(SSR,RRR),并且SR是有限生成投射的.

3)SSR≅HomROP(RSS,RRR),并且RS是有限生成投射的.

Frobenius扩张的研究通常会和另一种重要的扩张,也就是可分扩张联系在一起.

定义4一个环扩张S/R是可分扩张,如果S-双模同态π是可裂满的,其中

π:S⊗RS→S,s1⊗Rs2s1s2

一个环扩张S/R既是Frobenius扩张,又是可分扩张,则被称作一个可分的Frobenius扩张.

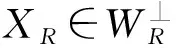
证明根据假设S/R是一个Frobenius扩张,则对任意的MR∈Mod-R,T(MR)=M⊗RSS≅HomR(SSR,MR)=H(MR).根据伴随同构,对任意的i≥1,

证明根据伴随同构,对任意的i≥1,

由于S/R是一个Frobenius扩张,RS为一个有限生成的投射R-模,因而W⊗RSR∈addWR.根据假设得到,对任意的i≥1均有

从而对任意的i≥1,

即得到

命题4设R是一个交换环,S/R是一个环的Frobenius扩张.若WR是一个广义倾斜R-模,则W⊗RSS是一个广义倾斜S-模.

证明由于RS是一个有限生成的投射模,则有W⊗RSS是有限生成的.对任意的i≥1,有

根据假设S/R是一个Frobenius扩张,RS作为R-模是有限生成投射的,从而W⊗RSR∈addWR.由于WR是自正交的,得到对任意的i≥1,

故

对任意的i≥1都成立,即S-模W⊗RSS是自正交的.

另一方面,因为WR是一个广义倾斜R-模,于是存在Mod-R中的正合列

其中对任意的i≥1,Ti∈addWR,且用HomR(-,WR)作用上述正合列仍正合.由于RS是有限生成投射的,用张量函子-⊗RSS作用后得到Mod-S中的正合列

其中对任意的i≥1,

Ti⊗RSS∈add (W⊗RS)S

考虑下面的复形同构,

其中第一个同构是由伴随同构得到.根据假设W⊗RSR∈addWR,由于HomR(T,W)是正合的,从而HomR(T,W⊗RSR)也是正合的,于是HomS(T⊗RSS,W⊗RSS)也是正合的.

综上所述,W⊗RSS是一个广义倾斜S-模.

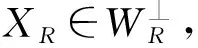
回想一个函子F:C→D称为Frobenius函子指的是存在一个函子G:D→C使得(F,G)和(G,F)都是伴随对.根据Frobenius扩张的定义,容易看出由双模AAS和SAA诱导的函子-⊗SAA≅HomS(AAS,-)是一个Frobenius函子.

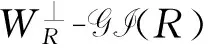
证明设T=-⊗RSS:Mod-R→Mod-S是由MSM⊗RSS对应关系得到的张量函子,则T≅H=HomS(AAS,-)是一个同时以限制函子F=-⊗sSR为左、右伴随的Frobenius函子.

根据定理1和定理2,分别得到

3 W⊥-Gorenstein内射维数

类似于一些经典的同调维数的定义,本文定义了模的W⊥-Gorenstein内射维数和环的整体W⊥-Gorenstein内射维数.

W⊥-GidR(M)=Inf{n|∃W⊥-Gorenstein内射分解0→M→E0→E1→…→En→0}

如果不存在这样的n,则记W⊥-GidR(M)=∞.

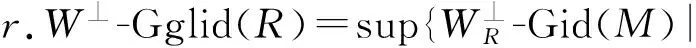
下面的命题表明一个模的W⊥-Gorenstein内射维数在Frobenius扩张下是“保持的”.

命题6设R是一个交换环,S/R是一个环的Frobenius扩张.对任意的R-模MR均有

证明首先断言

若W⊥-GidR(M)=∞,结论显然成立.

假设W⊥-GidR(M)=n<∞,则存在Mod-R中的正合列

0→M→E0→E1→…→En→0

0→M⊗RSS→E0⊗RSS→E1⊗RSS→…→
En⊗RSS→0

反过来,假设

对于R-模MR,存在Mod-R中的正合列

0→M→E0→E1→…→Em-1→Km→0

使得对0≤i≤m-1,Ei均是W⊥-Gorenstein内射模(事实上,可以都取内射模).由于RS是投射的,于是利用张量函子-⊗RSS作用后得到Mod-S中的正合列

综上,得到

推论1是命题6的一个有意义的推论.

推论1设S/R是一个环的Frobenius扩张.对任意的R-模MR,均有idR(M)=idS(M⊗RS).

命题7设MR是一个R-模,M′R是MR的一个直和项,则有

W⊥-GidR(M′R)≤W⊥-GidR(MR)

证明若W⊥-GidR(MR)=∞,则结论显然成立.令MR≅M′R⊕M″R,现设

W⊥-GidR(MR)=n<∞

对n应用归纳法.

若n=0,MR是一个W⊥-Gorenstein内射模,而W⊥-Gorenstein内射模是保持直和项的,故M′R也是一个W⊥-Gorenstein内射模.

若n>0,考虑正合列0→M′→I′→K′→0和0→M″→I″→K″→0,其中I′和I″是内射R-模.于是得到如下的交换图:

图1 交换图

其中列正合,行是可裂正合的.根据引理1,

W⊥-GidR(K′⊕K″)=n-1

利用归纳假设,

W⊥-GidR(K′)≤n-1

于是再利用引理1,得到

W⊥-GidR(M′)≤n

命题8设R是一个交换环,S/R是一个环的Frobenius扩张.对任意的S-模MS,

若此环扩张S/R也是可分的,则

则有Mod-S中的正合列

0→MS→E0→E1→…→En-1→En→0

0→MR→E0→E1→…→En-1→En→0

根据定理1,对每个0≤i≤n,Ei均是W⊥-Gorenstein内射的.从而有

反过来,若

W⊥-GidR(MR)=m

则有Mod-R中的正合列

0→MS→E0→E1→…→Em-1→Em→0

0→M⊗RSS→E0⊗RSS→E1⊗RSS→…→
Em⊗RSS→0

若环扩张S/R是可分的,则有MS是M⊗RSS的一个直和项,于是根据命题7,

综上,得到

推论2设S/R是一个环的Frobenius扩张.对任意的S-模MS,均有idR(M)≤idS(MS).特别地,若S/R同时是可分的扩张,则

idR(M)=idS(MS)

证明利用命题8,类似于推论1的证明.

推论3设R是一个交换环,S/R是一个环的Frobenius扩张.则

若此环扩张还是可分的,则

证明根据命题6,容易得到

若S/R是可分的,对任意的S-模MS,均有MS|M⊗RSS.因而,根据命题7得到

利用上述结果,可以得到环的整体维数是可分Frobenius扩张下的一个同调不变量.

推论4设S/R是一个环的Frobenius扩张,则

r.gldim(R)≤r.gldim(S)

特别地,若此扩张是可分的,则有

r.gldim(R)=r.gldim(S)

证明根据推论1和推论2容易得到.

致谢：本文得到浙江机电职业技术学院科教融合项目(A-0271-21-025)的资助，在此表示感谢.