GFRP层合板近缘和边缘低速冲击损伤数值模拟研究

徐姚兴， 韦尧兵, 刘俭辉

(1. 兰州理工大学 机电工程学院, 甘肃 兰州 730050; 2. 商丘工学院 机械工程学院, 河南 商丘 476000)

复合材料因比强度高、比刚度大、抗疲劳以及可设计性强等特点，被广泛应用于航空航天、汽车、船舶、军事等领域.飞机的机身、驾驶舱、机翼大多是使用复合材料构造的.当飞机受到低能量冲击时易产生损伤，这些能量冲击造成的材料损伤在表面无法观察到，但是内部损伤已经出现.这些冲击致使材料压缩强度大幅度下降，有些可以下降60%以上，造成材料综合性能下降[1-3]，进而对材料的安全性产生严重的影响.

以往的研究工作通常局限于构件的中心，远离边缘，很少关注近缘或边缘冲击.然而在飞机机翼、风力机叶片服役过程中发生的边缘撞击事件会导致严重的冲击损伤，使得复合材料结构过早被压缩破坏.沈真等[4]研究了复合材料体系的抗冲击性能，提出了复合材料抗冲击性能的2项指标，包括损伤阻抗和损伤容限.Malhotra等[5]研究了复合材料的冲击损伤，这些损伤发生在层合板的近缘和边缘上，并且对损伤大小和损伤机理进行了探讨，结果表明复合材料层合板易受边缘冲击.Ostré等[6]对碳纤维增强复合材料进行了低速边缘冲击和准静态实验，结果表明，2种材料的静态和动态行为是不同的，并且研究发现纤维性能控制初始冲击刚度，而在准静态压痕情况下，基体的性质控制初始压痕刚度与破碎的程度.Thorsson等[7]研究了聚合物基复合材料层合板在低速边缘冲击和冲击后压缩的实验响应，实验中使用了2种不同的冲击角度，即相对于边缘的0°与45°.Ji等[8]对复合材料层合板的冲击行为进行了实验和数值分析，研究了复合材料层合板在表面或边缘受到冲击时的冲击能量极限，由于多种失效模式的普遍存在，故采用了能够预测面内、面外损伤和失效模式的统一数值模型.

目前，复合材料冲击方面的研究已取得了一些成果[9],在复合材料冲击方面进行了相关研究，但主要是针对中心冲击造成的损伤，而对于近缘或边缘冲击对复合材料造成的损伤还未深入讨论.冲击位置不同，对构件造成的损伤亦不同.因此，本文以三维渐进损伤分析方法为基础，运用ABAQUS软件，插入0厚度的Cohesive单元来模拟界面层，结合改进的Vumat子程序对不同厚度层合板在不同能量下的冲击损伤进行仿真模拟，并通过实验数据验证模拟方法的有效性和可行性.

1 数值仿真理论

目前，三维渐进损伤方法已经被广泛用于复合材料的各种受力分析中，如冲击、疲劳载荷作用损伤分析等[10-12].通过此方法可以比较清楚地了解构件产生损伤后的应力重新分布情况及其损伤缓慢发展的过程.三维渐进损伤分析方法一般来说包含应力分析和失效分析:应力分析就是通过经典的复合材料层合板理论来进行有限元模拟分析;而失效分析一般是确定复合材料的失效判据和刚度退化方案，模拟纤维损伤断裂、基体损伤断裂和分层破坏.

1.1 失效判据

复合材料结构受到外界的低速冲击，损伤形式主要是纤维断裂、基体失效以及分层.本文基于应力的三维Hashin失效准则[13]来对纤维、基体损伤进行判断，具体失效判据如下：

1) 纤维失效

纤维断裂(σxx≥0)

(1)

纤维压缩(σxx<0)

(2)

2) 基体失效

基体开裂(σyy+σzz≥0)

(3)

基体挤压(σyy+σzz<0)

(4)

3) 层间损伤

对于分层损伤，引入0厚度Cohesive单元的失效判断系数GTC.

(5)

式中：σij为各单元方向与之相对应的应力分量；XT、XC、YT、YC分别为纤维方向极限拉伸强度、纤维方向极限压缩强度、垂直纤维方向极限拉伸强度、垂直纤维方向极限压缩强度；Sij为ij面内的极限强度；GⅠ、G分别为Ⅰ、型的断裂能；GⅠC、G分别为Ⅰ型临界应变能释放率、型临界应变能释放率；η为B-K准则系数.

只要某一单元的应力状态满足式(1～5)之一，则该单元发生了相对应的失效模式.

1.2 材料参数退化方案

复合材料层合板满足损伤判据之后，就需要对材料相关参数进行折减.参数退化方案一般有3种：

1) 材料损伤之后相关的参数进行倍速折减；

2) 材料参数通过指数函数进行折减；

3) 基于断裂韧性退化.

目前，Camanho退化方法[14]是常用的材料参数折减方案，具体步骤如下：

纤维断裂：E′11=FfE11

纤维压缩：E′11=FfcE11

基体开裂：

E′22=FmE22,G′12=FmG12
G′23=FmG23

基体挤压：

E′22=FmcE22,G′12=FmcG12
G′23=FmcG23

式中：Ff=0.07;Ffc=0.14;Fm=0.2;Fmc=0.4；E11、E22分别为纤维方向与垂直纤维方向弹性模量；G12、G23为剪切模量；E′11、E′22、G′12、G′23分别为损伤后材料对应的参数.

当发生纤维失效、基体失效时材料参数会发生变化，以往的研究直接把材料的相关参数进行折减.这种退化方法一方面会引起有限元计算中单元的极度扭曲，单元扭曲必然会使模拟结果误差较大；另一方面在材料破坏程度较轻的情况下，其失效单元还能承受多余的载荷，如果此时把材料刚度直接折减，那么有限元算出的承载能力值会减小.本文为了防止ABAQUS分析过程出现上述情况，将折减系数变为与时间有关的控制变量，借助材料损伤之后的参数进行倍速折减，具体步骤如下：

纤维断裂：E′11=F′fE11

纤维压缩：E′11=F′fcE11

基体开裂：

E′22=F′mE22,G′12=F′mG12
G′23=F′mG23

基体挤压：

E′22=F′mcE22,G′12=F′mcG12
G′23=F′mcG23

式中：F′f=1-0.93(c/t)2；F′fc=1-0.86(c/t)2；F′m=1-0.8(c/t)2；F′mc=1-0.6(c/t)2；c为ABAQUS内当前时间；t为冲击物在接触试件开始到速度为0的总时间，可以通过实验或有限元计算得出.

随着折减系数的加入，在ABAQUS计算过程中，材料折减便有具体的步骤，从而使有限元计算过程中不再出现极度扭曲现象或者当材料失效时还有多余的承载能力，提高了计算精度.

1.3 复合材料层合板低速冲击分析流程

在ABAQUS/Explicit模块中进行冲击损伤动态分析时，计算机会计算此刻的全部单元应力和应变，之后通过设定好的失效准则进行材料失效判断.如果应力和应变达到失效判据，则借助Vumat子程序里刚度退化方案进行相应的材料参数折减，之后重组刚度矩阵，ABAQUS便进行下一时刻冲击损伤分析，具体流程如图1所示.

图1 低速冲击分析流程图Fig.1 Flow chart of low velocity impact analysis

2 算例分析

为了验证模拟方法和子程序二次开发的正确性，基于复合材料层合板三维渐进累积损伤分析方法，在利用达索公司商用有限元软件ABAQUS的基础上，用二次开发子程序对层合板低速冲击进行动态模拟，并与实验结果进行对比.材料为GFRP层合板，铺层顺序为[0°/45°/90°/-45°]s和[0°/45°/90°/-45°]2s，尺寸为89 mm×55 mm(长×宽)，单层板厚度为0.25 mm.冲击器设定为刚体球形，直径为20 mm，质量为0.74 kg，并且为了使边缘冲击的层合板受力均匀，将边缘冲击与近缘冲击的冲击器形状设为不同，这是为了与文献实验边界条件相对应，层合板有限元模型设计如图2所示.本文采用带沙漏控制的8节点一阶减缩积分单元(C3D8R).考虑到冲击影响区域，在有限元模型网格划分时，采用渐进式的网格划分，使网格的密度从外部到冲击点逐渐增大，这样既可以保证结果的精度，又提高了ABAQUS的计算效率.玻璃纤维增强环氧树脂基复合材料单层板基本性能和材料属性如表1和表2所列，Cohesive单元属性如表3所列.其中，η为估计值.数值模拟5种不同入射能量对不同板厚(2 mm、4 mm)层合板造成的冲击损伤,研究不同入射能量对不同位置冲击损伤的影响.冲击器速度值与对应的能量值如表4所列.

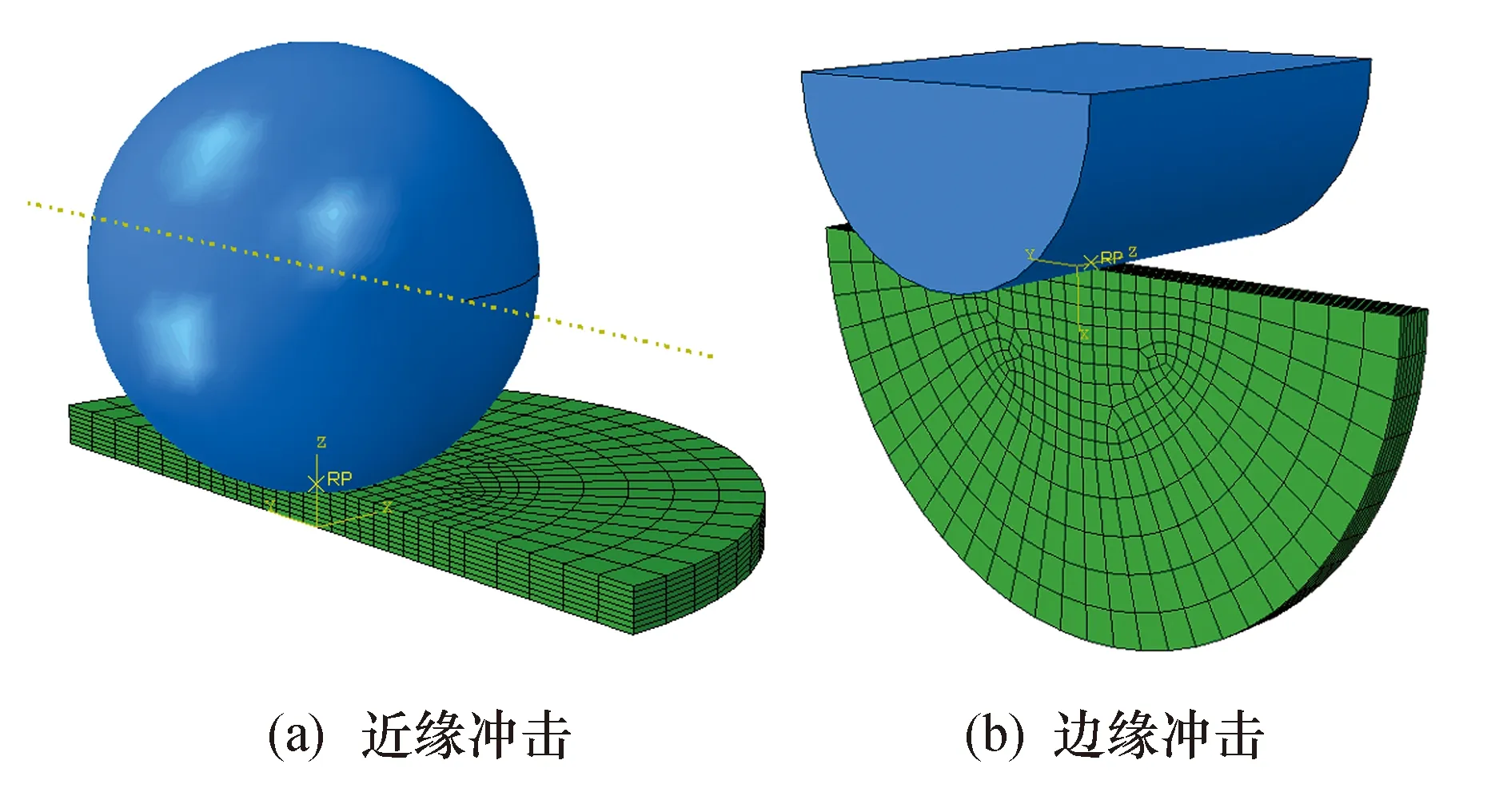
图2 有限元模型

表1 GFRP层合板基本性能参数[15]

表2 GFRP层合板强度属性[16-17]

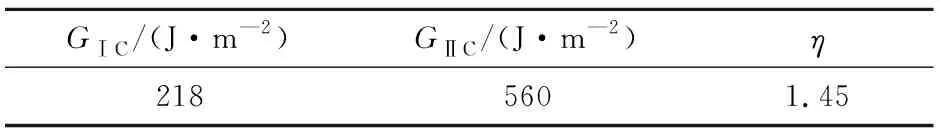
表3 粘性单元属性[17]

表4 入射能量与冲击速度对应值

2.1 层合板低速冲击损伤分析

2.1.1近缘冲击

选取厚度4 mm，冲击能量为2 J.图3为近缘冲击在冲击能量E=2 J下的渐进损伤过程.从层合板损伤过程可以看出：

图3 近缘冲击渐进损伤Fig.3 Impact progressive damage of near-edge

1) 在冲击刚开始时，层合板立即受到弯曲应力作用，其正面受压应力，而反面受拉应力，紧接着层合板便产生弯曲变形；

2) 随着冲击继续进行，层合板变形增大，可以清晰地看到接触点已经产生了明显的压痕，冲击反面因受到较大的弯曲应力使得层合板反面附近基体损伤迅速增大；

3) 在2 J能量冲击下，纤维并未发生损伤，说明试样整体应力还未达到纤维失效强度；

4) 无论在冲击的任一时刻，基体压缩损伤都大于基体拉伸损伤，且基体的碎屑粘结在一起，这也在一定程度上阻止分层的扩展.

上述观察到的现象与文献[15]利用计算机断层扫描得出的结果相一致.

2.1.2边缘冲击

选取厚度4 mm，冲击能量为2 J.图4和图5为边缘冲击在冲击能量E=2 J下的渐进损伤过程.从层合板损伤过程可以看出：

图4 边缘冲击渐进损伤Fig.4 Impact progressive damage of on-edge

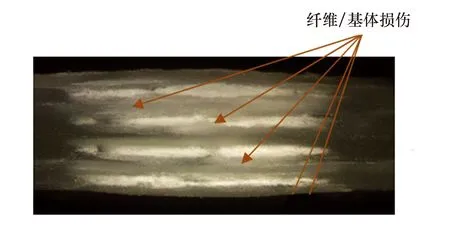
图5 冲击试件扫描结果Fig.5 Scanning results of impact test pieces

1) 在冲击点处，纤维断裂贯穿整个厚度方向，随着冲击的进行，纤维损伤从迅速增大到逐渐减缓；

2) 由于受力方向不一样，分层损伤与近缘冲击相比更加严重，这将导致材料的综合性能急剧下降；

3) 与近缘冲击相比，边缘冲击的纤维已经产生损伤，并且主要是压缩损伤，纤维产生破坏也将导致材料性能急剧下降；

4) 与近缘冲击一样，无论在冲击的任一时刻，基体压缩损伤都大于基体拉伸损伤，针对于此现象，后期设计复合材料时可以适当地增强基体的压缩强度.

上述观察到的现象与文献[15]利用计算机断层扫描得出的结果相一致.

2.2 层合板低速冲击动态响应分析

2.2.1近缘冲击

峰值力是冲击器与复合材料在冲击事件中的最大接触力，对分析复合材料层合板冲击损伤的严重程度具有重要意义.利用本文提出的方法对GFRP层合板在不同冲击能量下的最大接触力进行数值模拟，并与实验结果[15]进行对比，结果如表5、表6和图6、图7所示.

图6 近缘冲击最大接触力与能量关系Fig.6 Relationship between maximum contact force and energy of near-edge impact

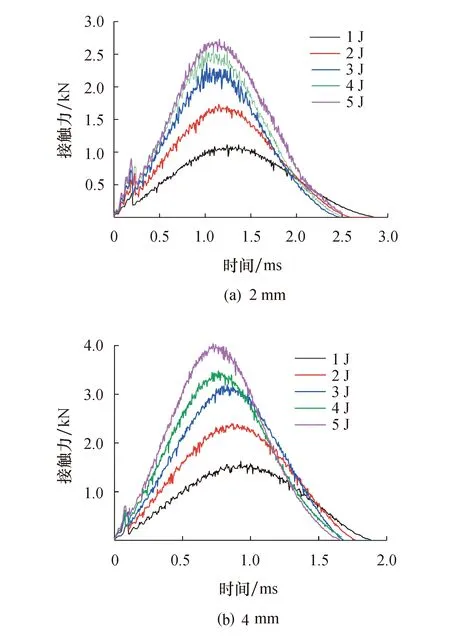
图7 近缘冲击时间-力曲线

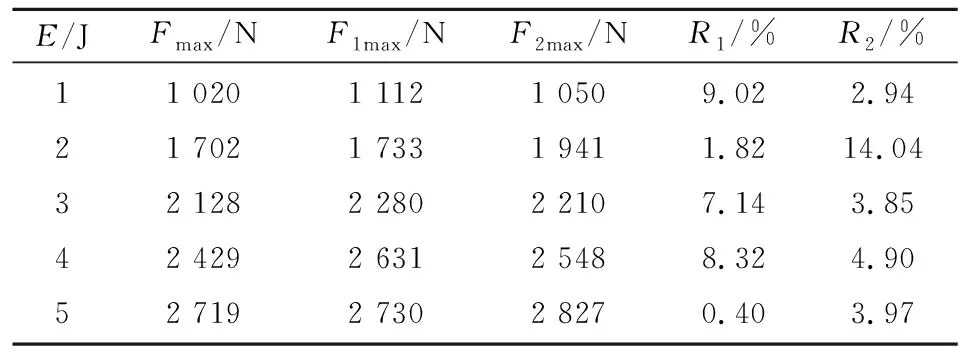
表5 厚度2 mm时不同冲击能量下最大接触力

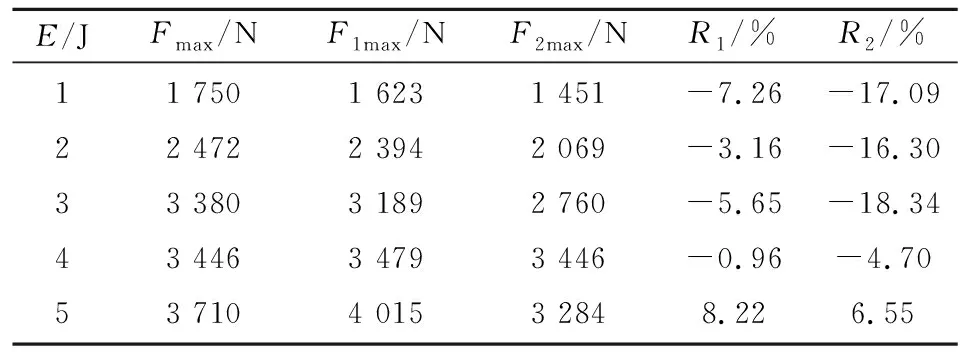
表6 厚度4 mm时不同冲击能量下最大接触力

表5和表6为2种Vumat子程序仿真结果与实验数据的比较.其中，E为冲击能量；Fmax为最大接触力实验值；F1max为改进后Vumat的最大接触力仿真值；F2max为未改进Vumat的最大接触力仿真值；R1和R2为误差值. 可以看出，在2 mm板厚情况下，刚度退化参数直接折减的方案比非线性折减的误差小，整体平均误差稍大些，但在4mm板厚的情况下，此方案所得出的结果误差较大.可能的原因是：2 mm厚的层合板抗冲击性能较差，冲击过程中材料破坏较严重，在有限元仿真时，一旦单元失效，此单元不能承受多余的载荷，单元的刚度便可直接倍速折减；而在4 mm板厚的情况下，冲击过程中材料破坏程度相比2 mm板厚要小，当单元发生失效，因厚度效应，其还能承受部分多余的载荷，此时用非线性折减刚度比较符合实际.

图6为最大接触力与冲击能量之间的关系.可以看出，无论是2 mm厚的层合板还是4 mm厚的层合板，在一定的冲击能量范围内，所受的最大接触力与冲击能量近似呈线性关系.考虑到散射带的影响，2种层合板厚度的峰值力随入射能量的增长率基本相同.

图7为2 mm和4 mm厚的层合板接触力-时间关系曲线，反映了有关损伤萌生和扩展的重要信息.随着冲击的进行，出现了第1个力的峰值，表示弹性响应极限载荷达到最大值，并且损伤已经开始，从此刻产生并传播3种不同类型的应力波，即纵波(P波)、横波(S波)和瑞利波(R波).接触力的第1次突然下降，表明分层造成了刚度的损失.整个过程受到的接触力近似对称，且近缘冲击响应几乎是正弦分布，2 mm和4 mm板厚除了一开始达到弹性响应极限载荷值之后，均无明显的尖峰，在达到最大接触力的一段时间内力的大小发生剧烈振荡.造成这种现象的主要原因是，在冲击器与层合板接触时间内，层合板内部已经出现了纤维损伤、基体损伤、分层，引起层合板与冲击器接触不稳定，从而导致力的变化.其余曲线上的小波动主要是由试件的弹性波响应和振动引起的.随着冲击器速度的增加，与层合板接触的时间越小.

2.2.2边缘冲击

数值模拟在5种不同入射能量下层合板边缘低速冲击对其造成的损伤，并与实验结果[15]进行对比，结果如表7、表8和图8、图9所示.

图8 边缘冲击最大接触力与能量的关系Fig.8 Relationship between maximum contact force and energy of on-edge impact

图9 边缘冲击时间-力曲线Fig.9 Force-time curves of edge impact

从表7和表8可以看出，2种厚度的有限元模拟中，非线性折减所得出的结果都比刚度直接折减的误差小，这表明对于边缘冲击，非线性折减的方案是比较符合实际情况的.可能的原因是，相对于近缘冲击，边缘冲击的破坏更为严重，在有限元中其失效单元也更多，如果是单纯地把失效单元刚度直接折减，则网格的扭曲数量更多，从而影响有限元的计算精度.从非线性折减方案结果可以发现，对厚板(4 mm)冲击时误差较小，而对薄板(2 mm)冲击时误差较大，且在冲击能量为5J时误差最大.可能的原因是：对薄板的冲击，冲击器下落的摩檫力对冲击能量的影响较大；薄板在受到冲击时易发生振动，对测量的准确性产生影响.

表7 厚度2 mm时不同冲击能量下最大接触力

表8 厚度4 mm时不同冲击能量下最大接触力

图8为边缘冲击最大接触力与能量之间的关系.可以看出，与近缘冲击类似，在一定的冲击能量范围内，所受的力与冲击能量近似呈线性关系.

图9为边缘冲击时间-接触力曲线.可以看出，每条曲线都存在明显的峰值，并且随着入射能量的增大而增大，达到最大接触力值的时间随着能量增大而减小，但是2种厚度的冲击接触时间几乎没明显变化.4 mm厚的层合板在边缘冲击期间的振荡较2 mm厚的层合板低，表明损伤较小或振动较小，而曲线上可见的小振动可能是由平面外的振动引起的.边缘冲击与近缘冲击在冲击时间-接触力曲线上有一定的区别，边缘冲击在冲击力达到最大值后会有一段平稳载荷区，之后冲击力再随时间缓慢下降，总的接触时间与近缘冲击相比更短.

3 讨论与分析

3.1 层合板低速冲击损伤对比分析

从2种冲击类型的GFRP层合板渐进损伤结果可知，在入射能量E=2 J情况下，近缘冲击的纤维还未产生损伤，而边缘冲击的纤维已经产生损伤，并且主要是压缩损伤.虽然都产生了不同程度的分层损伤，但对于近缘冲击而言，由于基体破碎的碎屑阻止分层的扩展，所以分层的损伤程度较边缘冲击低，并且边缘冲击的分层损伤呈现撕开状，这将导致材料的性能急剧下降.

3.2 层合板低速冲击动态响应对比分析

由模拟结果可知，边缘冲击的总接触时间都比近缘冲击的少很多，与板厚关系不大.这是因为层合板在近缘冲击下，与边缘冲击相比弯曲刚度低很多.较薄的层合板具有较低的冲击力，但具有较高的位移；而对于较厚的层合板，由于其较高的抗弯刚度，所以不太可能发生因弯曲而引起的位移，不过却更有可能在冲击器的前端发生剪切位移.在较高的冲击能级下，2种厚度的冲击响应都较为相似.

4 结论

本文采用了累积损伤分析方法，建立了复合材料层合板低速冲击三维数值模型，对层合板近缘和边缘低速冲击损伤进行了研究，得到了如下结论：

1) 通过与已有实验结果进行对比，发现与直接折减方案相比,利用本文给出的非线性折减Vumat子程序整体上能够更有效地预测层合板近缘、边缘冲击损伤以及时间-接触力曲线等主要特征.

2) 模拟计算结果表明近缘、边缘冲击表现出的冲击动态不同，边缘冲击接触的时间明显小于近缘冲击的，并且其最大接触力也远大于近缘冲击的，但2种冲击响应中都具有明显的接触力峰值.

3) 无论是近缘冲击还是边缘冲击，在冲击过程中基体压缩损伤都大于基体拉伸损伤.对于近缘冲击，基体损伤量要高于边缘冲击的.

4) 从模拟的渐进损伤图可知，边缘冲击造成的内部损伤程度都是高于近缘冲击的，并且其分层损伤也更为严重，为此，后期应该多加关注复合材料的边缘冲击损伤.

致谢：本文得到兰州理工大学红柳优青人才项目(2020062001)的资助，在此表示感谢.