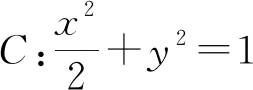一道清华测试题的解法探究和推广

浙江省衢州第二中学 (324000) 汪耀生

在解析几何研究中，圆和椭圆是两个非常重要的研究对象，它们图形优美，有极强的对称性，圆和椭圆可通过仿射变换相互转化，快速解决椭圆中相关的问题.椭圆中也会生成很多圆，比如内切圆、伴随圆、基圆和蒙日圆等，它们在性质具有怎样的关联？本文从一道清华自测题谈起，通过对问题的解法探究、拓展推广、链接应用等，建构这一类问题的解法，帮助学生抓住问题的本质，提升解决问题的能力，积累解题经验，优化思维品质，提升学生的核心素养.

一、真题再现

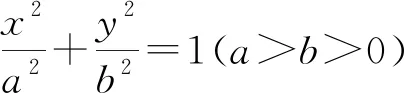
本题考查椭圆的几何性质，直线和椭圆的位置关系以及定值问题，意在考查学生数学运算能力、转化和化归问题的能力，以及数学运算和逻辑推理等核心素养.该题内涵丰富，是具研究价值的一道好题.

二、就题论题

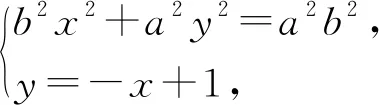
三、推广探究

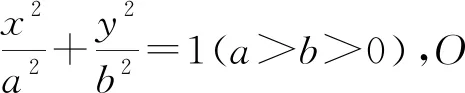
证明：若OM或ON中有一条直线斜率不存在，另一条必定为0，则|OM|=a,|ON|=b.

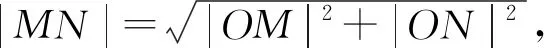
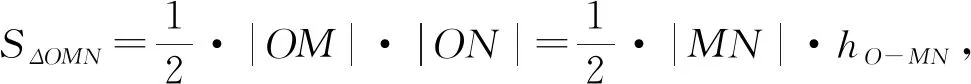
四、总结提升

上述问题我们可以这么描述：直线MN是椭圆基圆的任意一条切线，交椭圆于M,N两点，且OM⊥ON.事实上这也并不难证明(读者可自行完成)，至此我们得到：

对于双曲线也存在类似的结论，即：

结合以上结论，再来审视前面给出的例题，我们可以得到更准确而快速的解法：

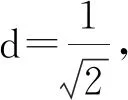
我们通过对一道清华测试题解法的研究，尝试去发现在OM⊥ON的条件下，椭圆长短半轴和|OM|,|ON|之间的关系，进而得到基圆，得到一般化的结论.在整个结论推导过程中，并未过多涉及直线MN，换言之，直线MN只是椭圆的一条割线这个简单的要求，这就为我们后续使用结论奠定了一个广泛的基础.在整个推导结论过程，先发现结论必要性，再证充分性，这种研究问题的方法也是我们需要掌握的一种常用方法.再根据椭圆研究结果，推广到双曲线，收获了双曲线的一般结论，这是我们在研究圆锥曲线这些“同根生”曲线，即截口曲线中常常会采用的一种方式.我们从特殊到一般，从椭圆类比到双曲线，经历结论的发现过程，让我们有一种“发现者、研究者和探究者”的满足感和成就感，会引导学生按图索骥，学生经历了发现问题、提出问题、分析问题和解决问题的全过程，会有探究结论的强烈愿望和冲动，充分调动学生学习数学的积极性，提升学生思维能力，提高学生的核心素养.

五、链接应用