统一定义在焦点弦相关问题中的妙用

甘肃省武威第十中学 (733000) 赵登祥

过圆锥曲线焦点的弦称为焦点弦，关于焦点弦问题，除了运用弦长公式外，常利用过焦点的特点，即用圆锥曲线统一定义求出焦半径，从而得到焦点弦的长，也可使与焦点弦相关的问题获得简解，达到优化解题、提高解题效率的效果．

圆锥曲线的统一定义：与定点(焦点)的距离与对应的一条定直线(准线)的距离的比等于常数(离心率e)的点的轨迹为圆锥曲线，当01时轨迹为双曲线，当e=1时轨迹为抛物线．

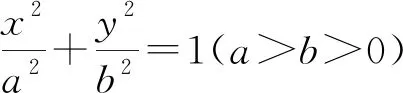
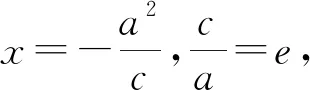
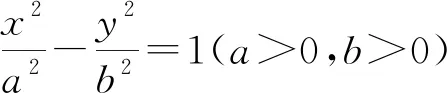
3、若|AB|是过抛物线y2=2px(p>0)的焦点F(c，0)的弦，则|AB|=x1+x2+p(证明留给读者)．下面举几例谈它们的应用．

一、在椭圆问题中的应用

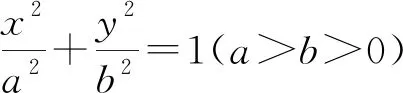
评注：通过将弦所在的直线方程与椭圆方程联立后，就容易求出弦长公式的x1+x2，这是解此类题中的一个重要步骤，而后面的解题就是根据题设和解题需要列式求解了．

评注：求椭圆方程必须分别求出a2,b2的值，所以必须寻找出两个方程，解题时要注意题设条件全面和反复运用，不能顾此失彼．

二、在双曲线问题中的应用

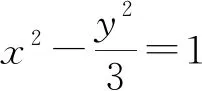
评注：关于双曲线的焦点弦有四种形式，需要针对不同的焦点与准线，在使用时可能会造成误用，当然在使用时，不必死记硬背，可以用定义进行推导一下，就能准确运用．

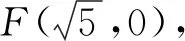
评注：要求焦点弦所在的直线方程，必须求出弦与双曲线的焦点，如果按常规方法是比较难办到的，在运用了焦半径的公式后，两个线段的比问题就能用坐标表示出来了，由定比公式又可得到另一个等式，下面的问题就很简单了．

三、在抛物线问题中的应用

例5 设O是抛物线的顶点，F为焦点，且AB为过F的弦，若|OF|=a，|AB|=b，求ΔOAB的面积．

评注：关于抛物线的焦半径是既好推导，也好记忆，也是我们解题中经常使用的一个结论，所以要经常使用它帮助解题．

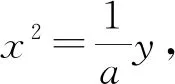
评注：此题的证明方法比较多，而这里运用抛物线的焦半径定理来证，显然推理通畅、过程简洁，体现了这个结论给我们解题带来的优势和方便．

上面由圆锥曲线统一定义推出了焦半径和焦点弦长公式，并举例讲述了几种应用题型，其实质就是统一定理的运用，在我们平时的教学中，若能经常教会一些解题方法和技巧，我想学生的学习兴趣和学习能力会得到较大提高的．