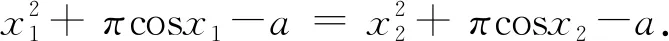2021年新高考Ⅰ卷导数压轴题的解法探析

福建省福清融城中学 (350399) 王 强福建省福清第三中学 (350300) 何 灯

历年高考试卷中的导数压轴题，都是命题专家的独具匠心之作．而双变量问题是其中的高频考点，高频考点之下必有变式，2021年全国卷导数压轴题其本身表述简洁，但解题的思想方法是灵活多样的，这有利于激发学生思维的灵活性．在解题中，若学生不能将题中的隐性信息识别转化，就无法打开解题思路，因此如何将所给条件进行转化成为解题的关键．本文对此类问题进行解法探究，总结处理此类问题的常用方法及基本思想，以期达到抛砖引玉之效．

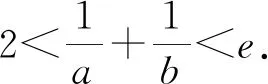
2试题解析第(1)问是常规的利用导数探求不含参函数单调性的问题由题易知f′(x)=1-lnx-1=-lnx(x>0)，令f′(x)=0得x=1，当x∈(0,1)时，f′(x)>0，从而f(x)在(0,1)上单调递增；当x∈(0,+∞)时，从而f′(x)<0，f(x)在(0,+∞)上单调递减．以下探讨第(2)问．

图1

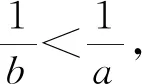
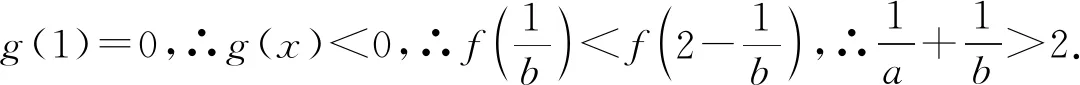
评注：若符合极值点偏移的题型设置，①f(x1)=f(x2)；②两根之和大于或小于2倍的极值点，x1+x2>2x0，x1+x2<2x0，则解决此类双变量问题的一般性策略步骤是：(1)设x2>x1，则x2>x0>x1；(2)x1和2x0-x2在f(x)同一个单调区间；

(3)f(x1)和f(2x0-x2)比较；(4)转化为单变量f(x2)和f(2x0-x2)比较；(5)利用极值点偏移的特点进行对称作差构造函数g(x)=f(x)-f(2x0-x).

图2

图3

图4

3变式训练已知函数f(x)=x2+πcosx-a在(0,+∞)上有两个零点x1，x2，且x1

通过以上分析可以发现，对于高考导数问题中出现的双变量的等式或不等式，要求我们必须具备转化意识，这样才能有效地解决问题．而此类问题若能用同构思想加以切入，辅以数学直观，就能把握其中所蕴含的减元、构造新函数、巧用单调性等数学思想．