青山缭绕疑无路,忽见千帆隐映来
——例谈“转换视角”在解题中的应用
广东省珠海市斗门区第一中学 (519100) 骆晓梅广东省深圳市深圳高级中学 (518118) 付中华
所谓转换视角,是指在解题过程中,遇到困难,转换思考问题的角度,寻找新的解题思路;或者是换个角度寻找其他的解题方法,优化解题过程,从而培养学生的解题能力,优化学生的思维品质,提升学生的数学素养.本文将借助几个具体的例子,与老师们分享.
一、转换视角,正难则反
例1 已知二次函数f(x)=4x2-2(p-2)x-2p2-p+1,若区间[-1,1]内至少存在一个实数c,使得f(c)>0,则实数p的取值范围是.
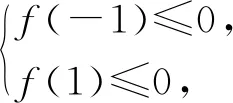

二、转换视角,化数为形
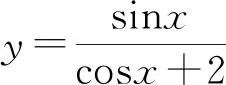
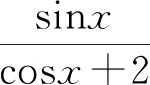
评注:对于此题转换视角,寻找代数式的几何意义,借助几何直观能够快速找到答案.
三、转化视角,化隐为明
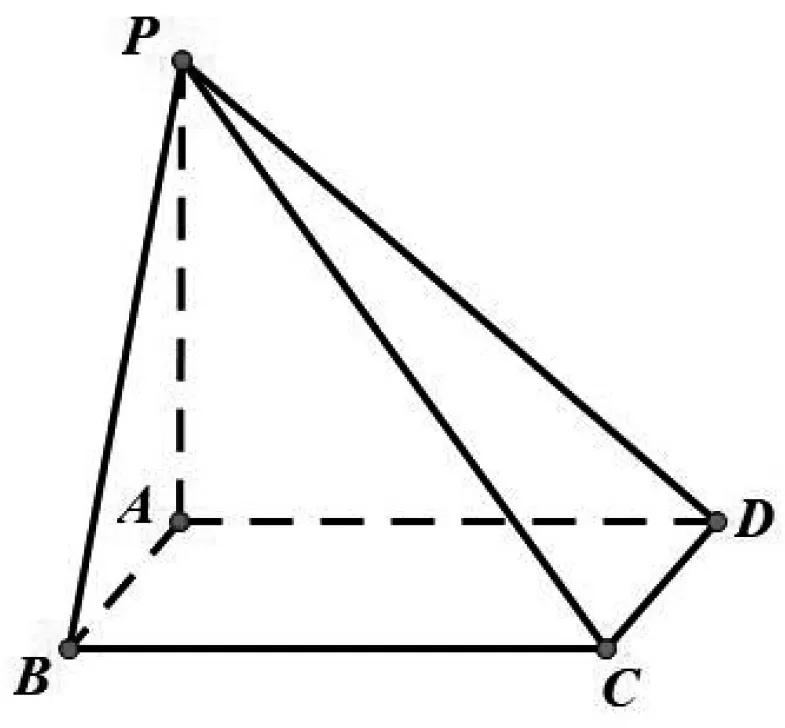
图1
例3 如图1,四棱锥P-ABCD中,ABCD为正方形,PA⊥平面ABCD,PA=AB,则平面PAB与平面PCD所成的锐二面角的度数为.

图2
解析:可将该四棱锥补成一个正方体,如图2,则所求的二面角转化为平面CDPQ与平面BAPQ所成的二面角,则∠APD就是锐二面角的平面角,易知∠APD=45°.
评注:按常规求二面角想法是作出它的平面角,而它是一个“无棱二面角”,要作出它的平面角有一定的难度.当然建系也是可行的,计算量稍微有点大.转换视角,将四棱锥补成熟悉的正方体,则可直接写出答案.
四、转换视角,借力助力
例4 求sin220°+cos250°+sin20°cos50°的值.

评注:学生的第一反应是采用降幂公式求解,但是困难重重.少数学生能够发现数据的特殊性,利用50°=20°+30°求解,能正确计算出结果的人则更少.通过对已知条件的观察,转换视角,构造对偶式,巧妙地利用了同角三角函数关系、二倍角公式两角和与差的正弦公式,化简之后容易发现角度的关系,从而配角40°=70°-30°,100°=70°+30°,或者利用和差化积公式,显得自然流畅.在解决此类三角函数求值问题中,该方法具有一定的通用性.
五、转换视角,以退为进


当n=1时,a1=S1=1(负值舍去);


六、转换视角,化异为同
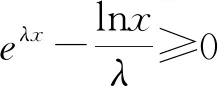

评注:本题中既含有指数式又含有对数式,无法直接求解参数的范围.转换视角,利用等式x=elnx将不等式左右两边转换为相同的结构,从而构造函数,简化原来的不等式.
七、转换视角,反客为主
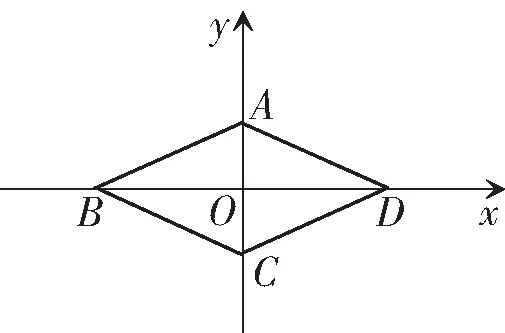
图3
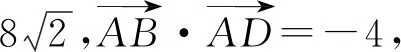
(1)求椭圆的方程;
(2)求证:AN与CM的交点在定直线y=1上.


评注:本题中,常规的化简方法是将x1+x2,x1x2代入,转化为含有k的式子,非常繁琐,转换视角,反客为主消去k,转换为含有x1,x2的式子,问题迎难而解.
以上是转换视角的常见思路和方法,在实际解题中还有其他的方法,比如说等价转换等等,故在平时的教学或解题中,需要我们不断总结,不断积累,提高学生的解题能力,培养学生的思维的灵活性,提升学生的思维品质,进而落实好学科核心素养.

