用题组促进数学概念课中的深度学习
浙江省衢州第二中学 (324000) 陈一晖
在高中数学概念课的教学过程中,从学生们理解概念到深化概念,再会应用概念解决问题是一个不断提高的过程,而此时常出现个别同学掉队,跟不上教学节奏的现象,这就是继续学习、深度学习的把控不够到位.如何使学生不脱节、不掉队,过好新概念学习这一关,是我们授课者必须深入思考的一个课题,本人通过近几年的教学实践进行了一些有针对性探索,感觉到利用设计题组进行目标训练是切实可行、效果显著的方法.本文向同行们分享一下,如何按照课情与学情的需要,设计对应学习题组以帮助提高数学概念课的教学效率.
1、通过题组探究数学概念的实质和内涵
有部分学生在刚开始接触新概念时,只是从字面上有所理解,还不能注意到细节,更谈不上理解概念的内涵,对实质性的东西是茫然的,此时我们应该设计一些对概念理解不透、容易出现解题偏差的题组,通过仔细分析、及时纠正错误,这样对巩固新概念很有用处.
案例一在巩固奇函数的概念时,我们可以设计如下的题组进行练习,旨在夯实概念.
⑴若函数f(x)的定义域为(-∞,+∞),且有f(-1)=-f(1),则f(x)是奇函数吗?

⑶函数f(x)=x3-x,x∈(-1,4]是奇函数吗?
⑷函数f(x)=ax2+bx能为奇函数吗?
⑸若函数f(x)奇函数,则一定有f(0)=0吗?
⑹如果函数f(x)=ax2+(2b-1)x,x∈(2b+1,1-b)是奇函数,求f(-1)的值.
分析:⑴由于奇函数的定义中是对于定义域内任意x,都有f(-x)=-f(x)成立,只有其中某一个或部分x满足等式是不能确定为奇函数的,故而答案为不一定.
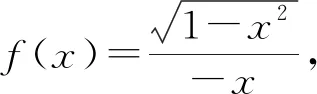
⑶中f(x)不是奇函数,由于f(-4)没有意义,则f(4)=f(-4)不成立.
⑷中f(x)可以是奇函数,当a=0,b≠0时满足.

⑹由于f(x)是奇函数,则必有a=0,且1-b=-(2+1),得b=-2,所以f(x)=-5x,x∈(-3,3),则f(-1)=5.
此组练习,从多个方面强化了奇函数的内涵,随着知识点的增加,当然还有多种类型的题目可以运用,应注意的是选题的广泛性和规范性,以及把握题目难易的坡度和区分度.
2、运用题组探索数学概念的外延和应用
一个数学概念本身不是孤立的,它是建立许多知识点的累积之上的,而一个新概念也需要与已学过的知识进行融合、交汇,形成知识网络,这样这个概念才有意义和存在价值.注意这里的外延是有限度、有方向的,也就是常说的所谓“正迁移”,如果迁移过分或迁移不当,有可能发生谬误.
案例二在学完抛物线的定义和标准方程后,我们可以给学生提供如下的一组提高练习,旨在理解抛物线概念并合理外延概念的作用.
⑴抛物线y2=4x上一点P到y轴的距离为4,求点P到焦点距离;
⑵已知动点P到点A(0,8)的距离比到直线l:y=-7的距离大1,求动点P的轨迹方程;
⑶若点A的坐标为(3,2),F是抛物线y2=2x的焦点,点M在抛物线上移动时,使|MF|+|MA|取得最小值的点M坐标为;
⑷过抛物线x2=4y的焦点F作一条直线交抛物线于P1(x1,y1),P2(x2,y2)两点,若y1+y2=6,则|P1P2|的值为.
分析:⑴由抛物线方程知,2p=4,所以准线方程为x=-1,而点P到y轴的距离为4,则点P到准线的距离为5,根据抛物线的定义知,点P到焦点距离为5.
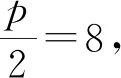
⑶ 由于|MF|是点M到抛物线焦点距离,使|MF|+|MA|取得最小值的点为过点A作与y轴垂直的直线与抛物线的交点,则点M纵坐标为2,代入方程的横坐标也为2.
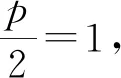
此组练习都是以抛物线的定义为基准,围绕着这个定义向四周辐射所形成的各类问题,通过本组题的练习,不但深化了抛物线的概念,同时也了解了哪些题是可以运用定义解决的.
3、运用题组辨别形似但本质不同的相关概念
有一些数学概念其表现形式差别不大,容易混淆,但是我们可以通过设计相关题组的方法,把它们放在一起解决,通过分析可发现它们之间的本质是不一样的,通过设计题组及时区分,并解剖它们的本质,可以进一步加深对所学概念的理解,以免犯审题不清造成的错误.
案例三在讲完了分段函数的单调性问题后,可以给出下面一组练习,旨在检查对一些分段函数单调性有关题型的判断情况.
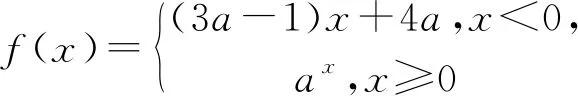
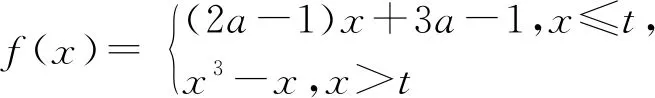

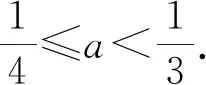
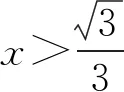
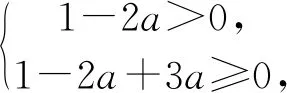
此组练习都是关于分段函数的单调性问题的,其题设部分比较相似,而不相似的部分正是问题的关键,通过分析研判,可以挖掘利用它们的不同,建立符合题意的求解方案.
4、利用题组多向探究发掘数学概念的用途
在一个概念的后面,会有许多对应的练习题目呈现,对此我们必须对它们进行分类和挑选,目的是有针对性地巩固所学的新概念,并使概念发挥作用.同时也可利用对新概念的认识,揭示一些问题的破解方法,扩大学生们视野,提高应变能力,增加学习数学的兴趣.
案例四在讲完函数的最大值与最小值的概念后,给出下面的题组,引导学生对函数的最大值与最小值的概念有一个全方位的了解.
⑴函数f(x)=x3-3x-1,若对于区间[-3,2]上任意x1,x2,都有|f(x1)-f(x2)|≤t,求实数t的取值范围;
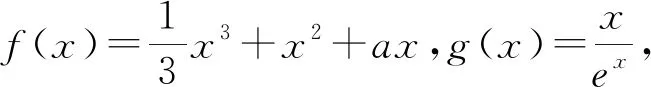

分析:⑴由于f′(x)=3x2-3,当x∈(-∞,-1)∪(1,+∞)时,f′(x)>0,当x∈(-1,1)时,f′(x)<0,易得f(x)max=1,f(x)min=-19.由题设知在区间[-3,2]上f(x)max-f(x)min≤t,从而t≥20,即实数t的取值范围是[20,+∞).
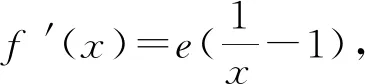
此组题,从形式上看似乎是不同类型的问题,但实质是一样的,它们都是通过求函数的最大值和最小值来解决问题,是函数最值问题的不同应用而已.

