Hénon-Heiles可积系统的Eisenhart提升

李 雯，章 海

（安庆师范大学 数理学院，安徽 安庆 246133）

可积系统具有良好的动力学行为，蕴含丰富的代数结构。人们发展了各种方法来构造新的可积系统，有些属于直接的方法，有些是代数或几何的方法。Eisenhart提升[1]是一种构造可积系统的有效方法，通过扩大相空间的维数，能获得高维相空间上可积的测地系统。文献[2-3]讨论了Goryachev-Chaplygin陀螺和Kovalevskaya陀螺的提升，获得了带有高阶Killing张量的四维时空的例子。从经典的Drach系统出发，文献[4]导出了一些具有自对偶和反自对偶的四维时空（它们都是Ricci平坦时空的例子），并研究了这些时空的Killing张量和等距群。文献[5-6]分别研究了经典的可积Toda链和Calogero系统的Eisen‐hart提升。Calogero系统的共形不变量在构造动力学不变量方面起到了很大的作用。Euler双引力中心问题被提升为三维的可积测地系统，相应的可积自然系统（包含势能项）也被构造了[7]。Hénon-Heiles系统是一类重要的物理模型，有一些可积的情形和很多可积的推广[8]。本文针对三种已知的可积情形，研究其单坐标扩充Eisenhart提升，获得新的三维系统，并讨论其可积性质。首先，回顾Hénon-Heiles系统及可积扰动的基本知识和Eisenhart提升方法。其次，根据Hénon-Heiles系统的三种可积情况和各自的扰动，通过引入一个额外的维度，提升原始系统，得到新的系统；原始系统的守恒量被提升成为新系统的守恒量。最后，得到相应的构形空间的高阶Killing张量。

1 预备知识

1.1 Hénon-Heiles可积系统及其可积扰动

1964年，文献[9]引入了原始的Hénon-Heiles系统：

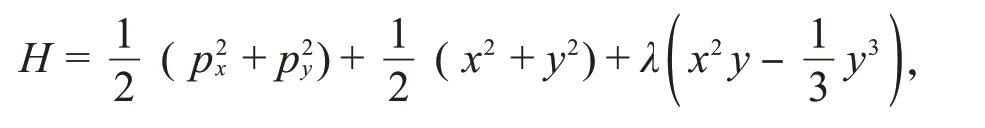
它被用于刻画在星系势场中恒星的运动规律。人们发现该系统表现出混沌的动力学行为，是不可积系统[10]。通过改变系统参数，该系统被推广为含多个参数的Hamilton系统：

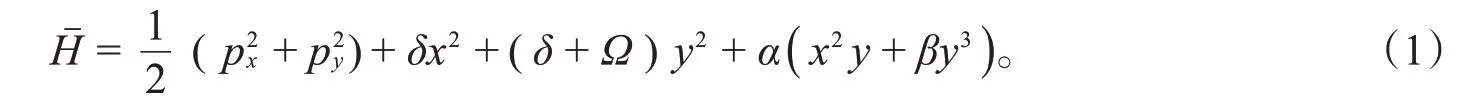
势能项的简单性以及参数不同值对应的动力学行为的丰富性导致系统（1）成为研究二维Hamilton系统的重要模型。可以从不同角度（包括量子化系统的角度）研究Hénon-Heiles系统由可积到不可积范畴的转变。对于一般的参数值，Hénon-Heiles系统是不可积的，但是在以下3种特殊的参数值情形下是可积的[11]：Sawada-Kotera(S-K)情 形，β=1/3，Ω=0；Kaup-Kupershmidt(K-K)情 形，β=16/3，Ω=15δ；Kortewed-de Vries(KdV)情形，β=2，Ω是任意的。它们的第二守恒量( {F,H}=0)分别是：

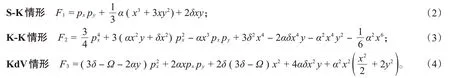
这3个系统分别对应于Sawada-Kotera方程、Kaup-Kupershmidt方程、5阶Kortewed-de Vries方程的定常流[12]。S-K-Hénon-Heiles系统在旋转笛卡尔坐标系中可分，KdV-Hénon-Heiles系统在平移的抛物坐标系中可分。K-K-Hénon-Heiles系统的广义可分性通过正则变换得到了证明[13]。

作为一类重要的可积系统，Hénon-Heiles系统有很多种推广和扰动方式，且得到的系统仍然具有可积性。下面介绍Hénon-Heiles系统的一些常见扰动形式[8]。

通过在S-K-Hénon-Heiles系统中增加一个离心项，得到可积的扰动系统：

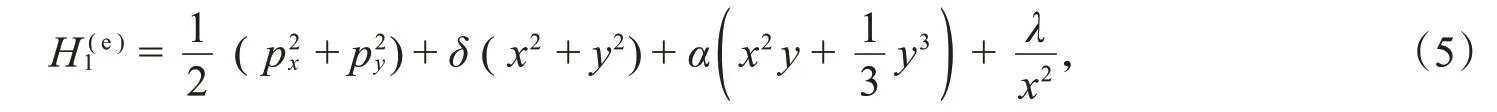
其守恒量为动量的四次多项式：

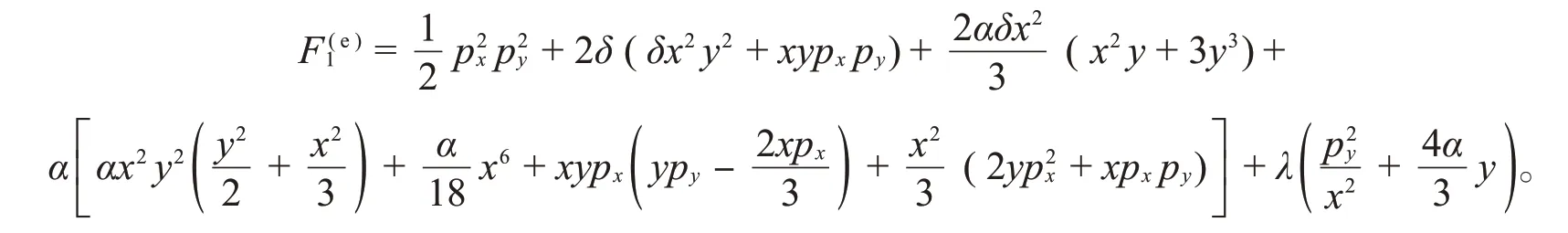
和原始系统相比，上述守恒量变成了四次不可约多项式，所以扰动后的系统不再是可分系统。

K-K-Hénon-Heiles系统的下述扰动由两个有理项给出：

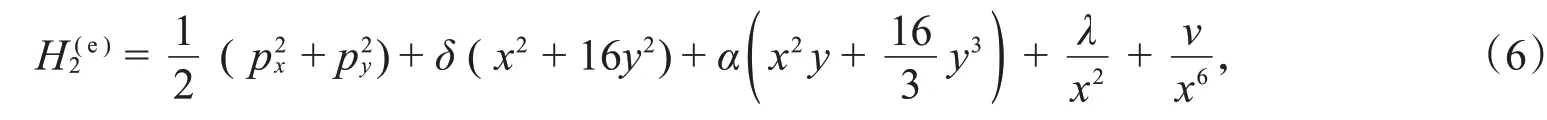
其守恒量也是动量的四次多项式：

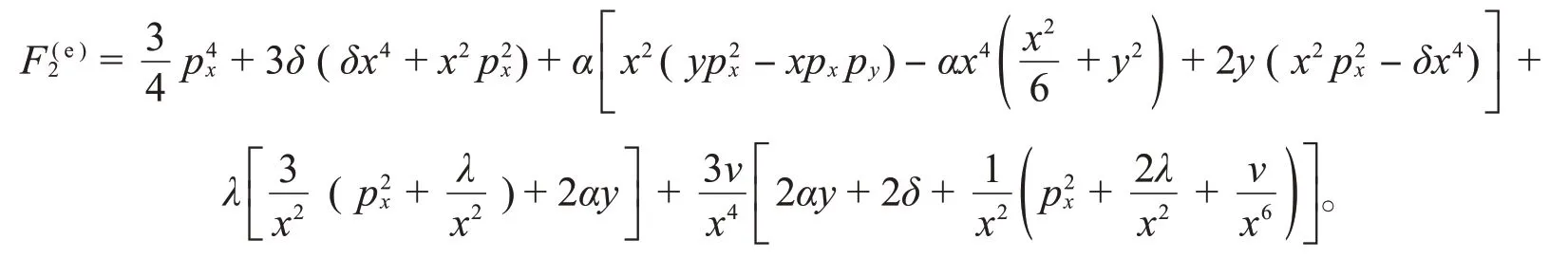
通过添加一个离心项可以得到KdV-Hénon-Heiles系统的扰动系统：

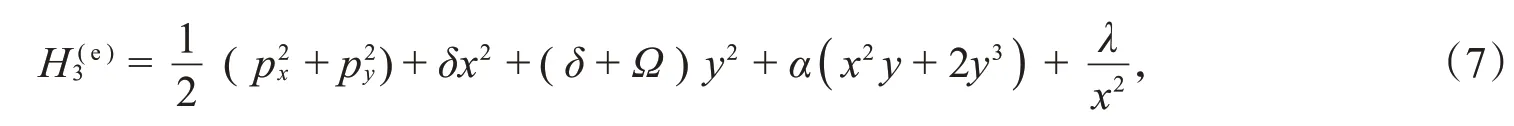
其守恒量是动量的二次多项式：

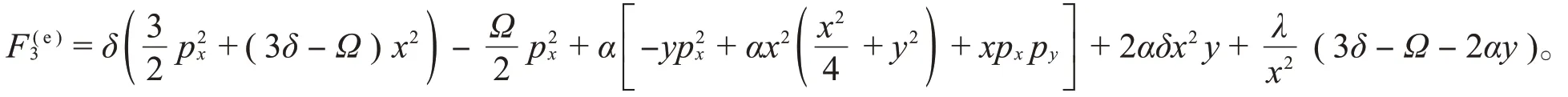
扰动保持了系统Hamilton-Jacobi方程的可分性，当然系统的分离坐标可能也有扰动。

1.2 Eisenhart提升方法

Eisenhart提升最早由Eisenhart引入[1]，它把平面上一个自然Hamilton系统的运动轨迹解释为弯曲空间上的测地线。这一构造与Jacobi度量[14]有一定的相似之处，但与Jacobi度量不同的是，Eisenhart提升要求扩大Hamilton系统的维数，通过引入一个或者多个额外的空间维度，把粒子在势场中的运动转化为不受作用的自由运动。Eisenhart提升方法可以很容易地从Hamilton动力学的基本原理得到[15]。

考虑一个自然Hamilton系统，它的Hamilton函数是动能和势能和的形式：

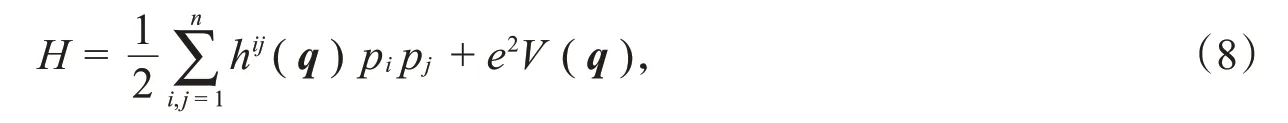
其中，(hij)是对称的非退化矩阵，h ij(q)和V(q)都是位置变量q=(q1,q2,q3,…,q n)的函数，p=(p1,p2,p3,…,p n)是与之共轭的正则动量变量。通过引入一对新的共轭变量(u,p u)，可以得到一个新系统的Hamilton函数

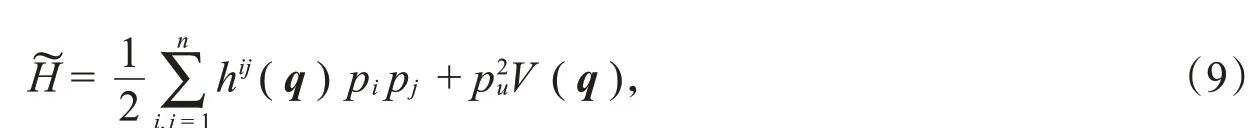
该函数没有势能项，是构形空间上的测地系统。上点的坐标为(q,u)，动量的二次多项式（9）对应于流形上的度量张量：

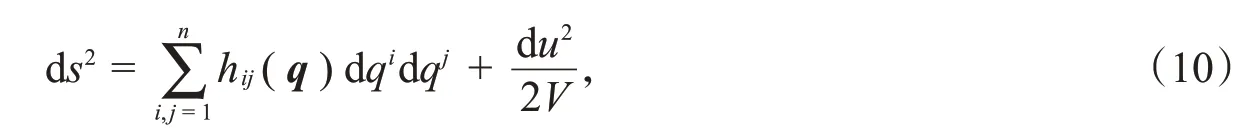
这里(h ij)是(hij)的逆矩阵。原始系统的运动方程包含在此度量决定的测地线方程中。利用Eisenhart方法获得的Hamilton函数是关于动量(p i,p u)的二次齐次多项式。设原始系统有一个守恒量( {H,F}=0)

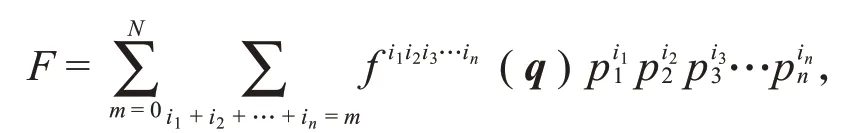
它是动量的N次多项式，最高次系数不全为零。多项式F经提升后，变为扩张相空间上的关于动量的N次齐次多项式是新系统的守恒量，这里{·,·}′表示扩充相空间上的Poisson括号。

如果原系统是电磁型系统[16]，系统的势能既包含纯量势V(q)，也含有向量势A i(q)，它的Hamilton函数是

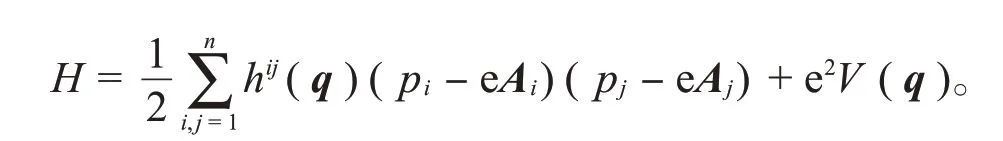
类似地，引入新的共轭变量(u,p u)，由Eisenhart提升得到的新Hamilton函数[13]

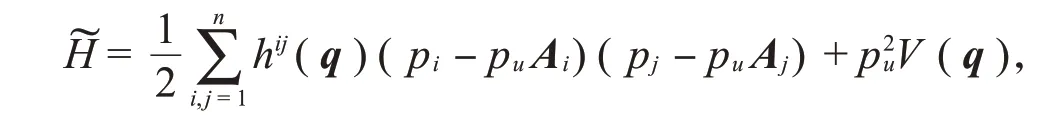
它可以看作（伪）黎曼流形(Q,ds2)上的测地Hamilton系统，其度量为

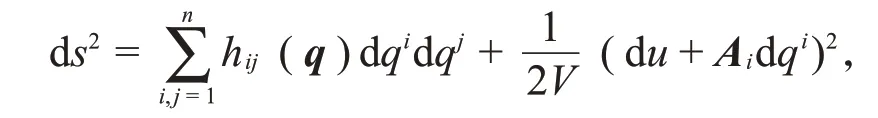
多项式守恒量也可以类似地得到提升。

2 用Eisenhart方法提升Hénon-Heiles系统

利用上一节介绍的Eisenhart提升方法，对Hénon-Heiles系统的3种可积情形及其可积扰动分别进行提升，推导新系统的Hamilton函数和守恒量，并给出构形空间上的Killing张量。

2.1 S-K-Hénon-Heiles系统

考虑Hénon-Heiles系统的第1种可积情况，利用Eisenhart提升方法，引入一对新的共轭变量(u,p u)，得到新系统的Hamilton函数是

由于u是可遗变量，L=p u是新系统的守恒量。提升原来的守恒量（2），得到新系统的守恒量：

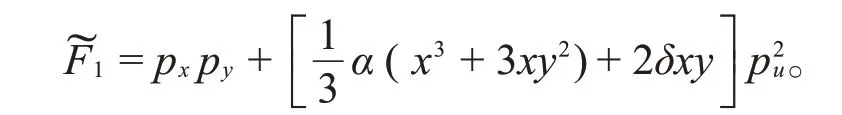
三自由度的新系统具有守恒量,L,，并且它们之间是函数无关的，因此提升后的系统也是可积的Hamilton系统。由于是(p x,p y,p u)的齐次多项式，它对应于扩张的构形空间上的（反变）Killing张量，其分量为

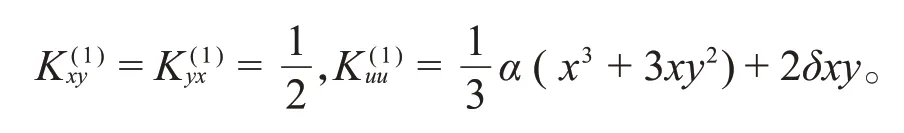
2.2 K-K-Hénon-Heiles系统

对于第2种可积情况，用Eisenhart方法提升得到新系统的Hamilton函数：

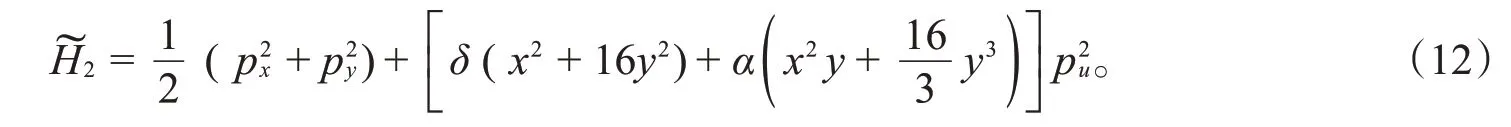
提升原系统的守恒量（3），得到新的守恒量：

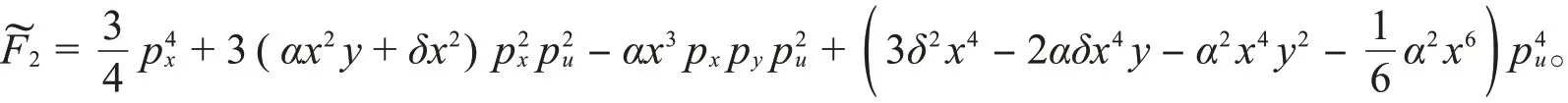
新系统具有守恒量,L,,它们之间是函数无关的，因此提升后的系统也是可积的Hamilton系统。

四次守恒量对应于系统的三维黎曼构形空间上的四阶（反变）Killing张量K(2)，K(2)的分量为

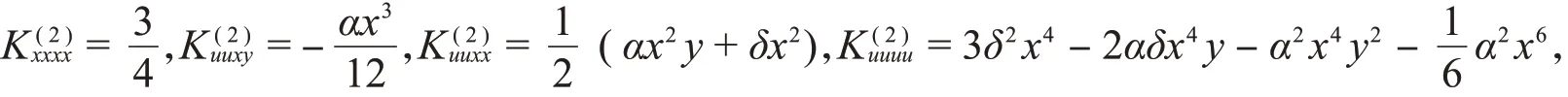
张量K(2)的其他分量可以由全对称性得到，所有对称化分量都未出现的分量为零。

2.3 KdV-Hénon-Heiles系统

考虑第3种可积情况，用Eisenhart方法提升得到新系统的Hamilton函数：

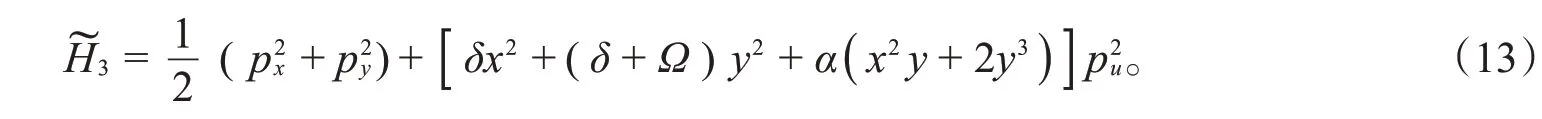
提升原系统的守恒量（4），得到新的守恒量：

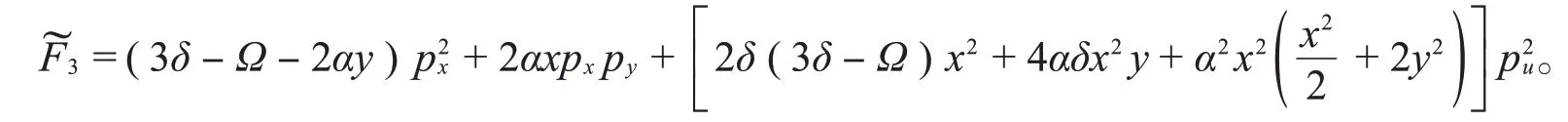
新系统具有守恒量,L,，它们之间是函数无关的，因此提升后的系统也是可积的Hamilton系统。

二次守恒量对应于系统的三维黎曼构形空间上的（反变）Killing张量K(3)，K(3)的分量为

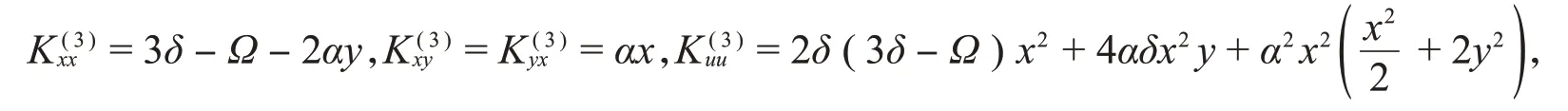
其他未出现的分量为零。

2.4 S-K-Hénon-Heiles可积扰动系统

对于S-K-Hénon-Heiles的可积扰动系统（5），用Eisenhart提升得到新系统的Hamilton函数：

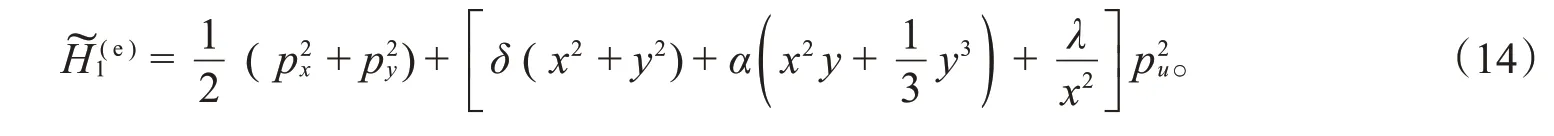
提升原系统的守恒量，得到新的守恒量：

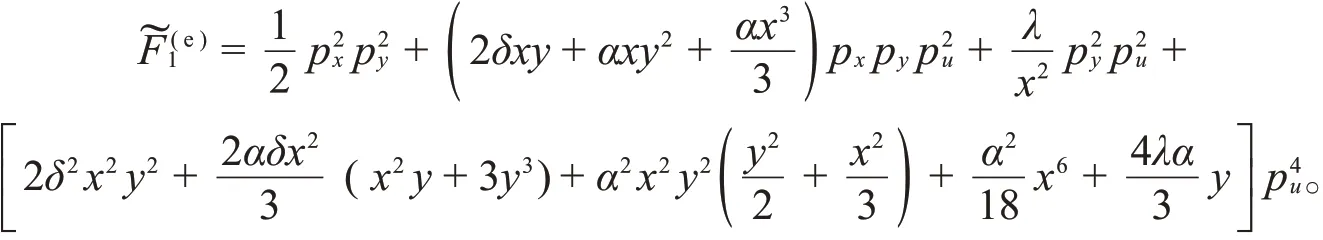
新系统具有守恒量,L,,它们之间是函数无关的，因此提升后的系统也是可积的Hamilton系统。

四次守恒量对应于系统的黎曼构形空间上的（反变）Killing张量K(4)，K(4)的分量为

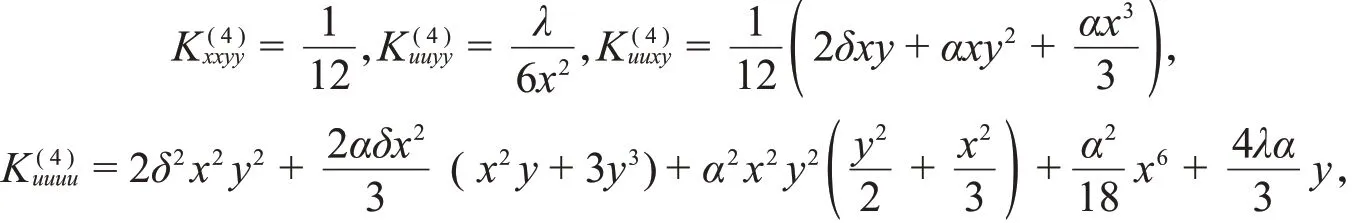
张量K(4)的其他分量可以由全对称性得到，所有对称化分量都未出现的分量为零。

2.5 K-K-Hénon-Heiles可积扰动系统

对于K-K-Hénon-Heiles的可积扰动系统（6），用Eisenhart提升得到新系统的Hamilton函数：

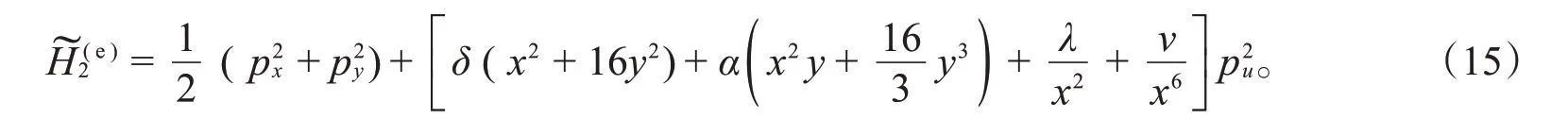
提升原系统的守恒量，得到新的守恒量：

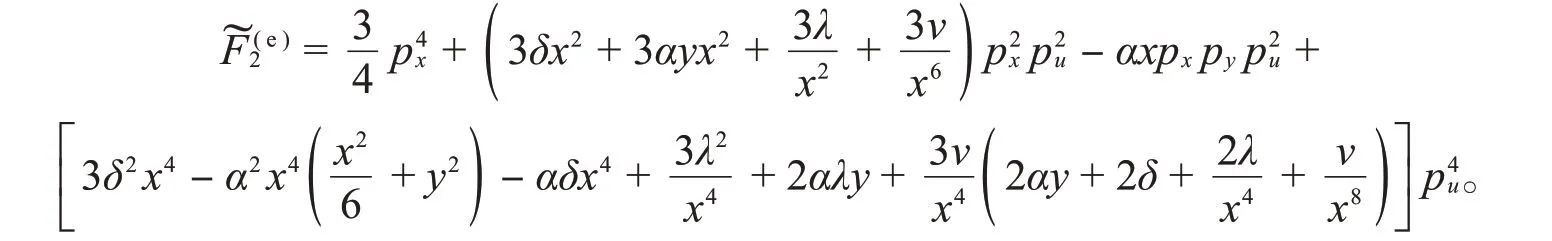
新系统具有守恒量,L,,它们之间是函数无关的，因此提升后的系统也是可积的Hamilton系统。

四次守恒量对应于系统的黎曼构形空间上的（反变）Killing张量K(5)，K(5)的分量为

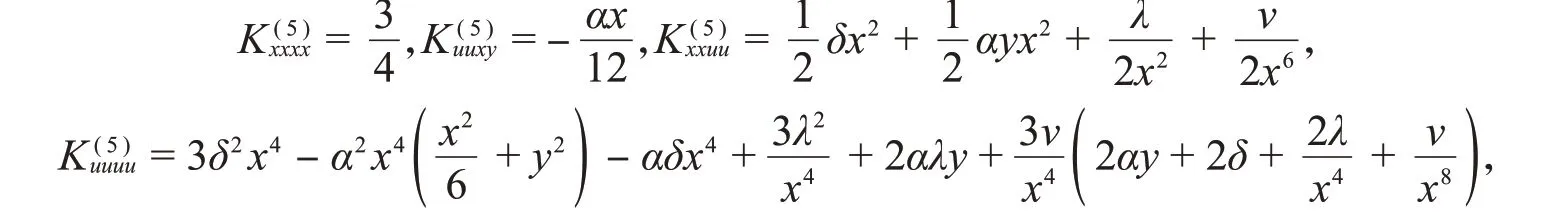
张量K(5)的其他分量可以由全对称性得到，所有对称化分量都未出现的分量为零。

2.6 KdV-Hénon-Heiles可积扰动系统

对于KdV-Hénon-Heiles的可积扰动系统（7），用Eisenhart提升得到新系统的Hamilton函数：

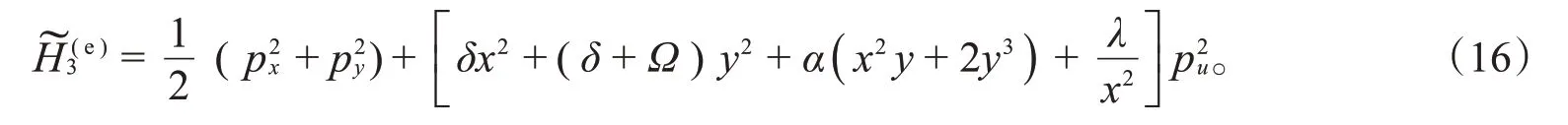
提升原系统的守恒量，得到新的守恒量：

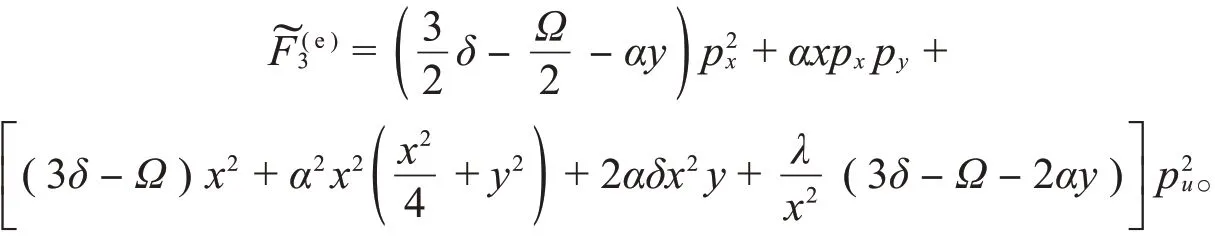
新系统具有守恒量,L,，它们之间是函数无关的，因此提升后的系统也是可积的Hamilton系统。

二次守恒量对应于系统的黎曼构形空间上的（反变）Killing张量K(6)，K(6)的分量为

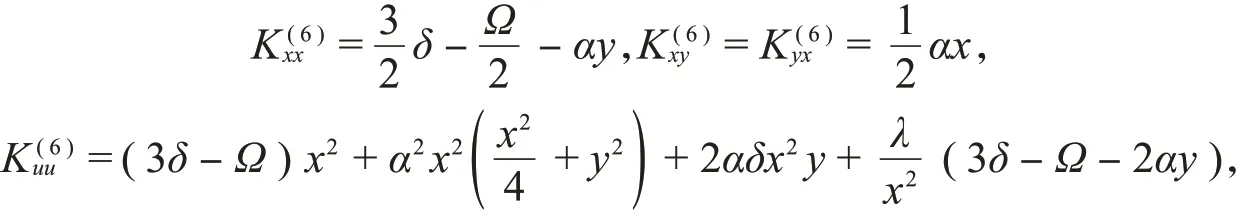
其他未出现的分量都为零。

系统的守恒量关于动量是一次、二次多项式，说明提升后的系统的Hamilton-Jacobi方程依然是可分的，其分离坐标由原系统（7）的分离坐标和新坐标u构成。可以继续研究该系统是否为多可分系统，即它是否具有超可积性。

3 结论

通过在相空间中引入一对额外的共轭变量(u,p u)，相空间的维数增加了两维。对于Hénon-Heiles系统的3种可积的情形及其扰动系统，我们推导了新系统的Hamilton函数、守恒量，得到了三维Riemann流形上的高阶Killing张量，这项研究在几个方向上可以继续进行。首先，可以尝试引入两个或者多个坐标变量，从而得到更高维的时空流形，并进一步研究这些时空的几何性质；其次，除了来源于原始系统守恒量的对称性，研究新系统是否还有额外的新的对称性，即新系统是否是超可积系统；最后，本文得到的系统都是测地系统，增加何种势能项之后是否仍保持系统的可积性？这些都是值得继续研究的新问题。