在“凑整”过程中提升简便运算能力
熊瑞峰 董涛


简便运算是综合运用计算原理,将较复杂的计算变得简单的一种技能。简便运算与运算定律的教学密切相关,蕴含着转化思想、整体思想、优化思想等数学思想方法。教学中,如何帮助学生明晰算理、掌握运算技巧、感悟运算之道呢?本期,我们讨论如何提升学生简便运算的能力。
把某些数凑成整十、整百,或把某个图形拼成一个完整图形,进而把握它们之间的内在联系,运用整体思想解决实际问题,是提升简便运算能力的常用方法。
一、凑整,培养思维的多样性
凑整是整体思想的重要组成部分。“凑十法”是凑整的一种,包括“拆小數,凑大数”和“拆大数,凑小数”两种方法。笔者在学生掌握了“拆小数,凑大数”的基础上,再教学“拆大数,凑小数”的方法。这样可以使学生明白,在计算20以内进位加法时,有多种不同的计算方法。
教学人教版数学一年级上册第92页例3时,笔者首先呈现“8+9=£”,组织学生观察拆分8或9凑成10的操作过程,直观感受拆数、凑整的基本思路。
生1:我的方法是把8凑成10。从9中分2给8,8添上2就是10,把10当作整体,10个1就变成了一个10,9分走2还剩7,10加7等于17,所以8+9=17。
生2:我的方法是把9凑成10。从8中分1给9,9添上1就是10,把10当作整体,10个1就变成一个10,8分走1还剩7,10加7等于17,所以8+9=17。
师:除了这两种方法,你还有其他方法吗?
生3:还可以根据9+8=17,得出8+9的得数也是17。
师:从生3的回答,你发现了什么规律?
生4:我发现两个数相加,交换加数的位置,得数不变。
笔者继续设疑:把9分成几和几才能跟8凑成整十?一名学生说:把9分成2和7,8和2凑成整十。笔者追问:空格中能填7和2吗?这名学生接着回答:不能,因为8和7不能凑成整十,所以两个空格中只能填2和7。笔者反问:把8分成几和几才能和9凑成整十?一名学生抢答:把8分成7和1,1和9恰好凑成整十。笔者追问:两个空格中能填1和7吗?他接着回答:不能,因为7和9不能凑成整十,所以不能填1和7。
最后,笔者问学生:你喜欢哪一种方法?学生回顾、比较,用自己喜欢的方式进行计算,进一步理解了不同“凑整”方法的算理。
经历多层次的活动,学生从具体到抽象,把“算”与“思”相结合,使思维过程更清晰、更有条理,既巩固了“凑十法”,又体会到简便计算的多样性。
二、凑整,培养思维的灵活性
教学《运算定律》时,笔者直接呈现例4(如图1),引导学生观察例题中的信息。
学生很快列出算式:234-66-34。笔者引导学生观察图中三名小朋友的算法,了解三种算法的特点,感悟计算的算理。他们是怎样计算的?一名学生回答:第一名小朋友是从234中依次减去66和34两个数;第二名小朋友是从234中减去66与34两个数的和;第三名小朋友是从234里先减去第二个数34,再减去第一个数66。
笔者借助小精灵的第二个提示“你喜欢哪种方法”,要求学生在小组中交流自己喜欢的方法,每个小组选一名代表汇报。第一小组说:我们喜欢第二名小朋友的算法,理由是减去的两个数的和恰好等于100,从234里减去100比较简便。第二小组说:我们喜欢第三名小朋友的算法,理由是从234中先减去第二个数34正好等于200,再从200里减去66比较简便。笔者顺势问:有谁喜欢第一名小朋友的算法?学生都表示不喜欢。笔者立即更换数据问:如果将题中的“234”换成“266”,第一名小朋友的算法简便吗?第三小组说:简便,因为266先减66得整数200,再从200里减去34比较简便。
通过不同方法的计算与比较,学生不仅发现“一个数连续减去几个数,可以减去这几个数的和”,而且明白了在计算过程中,需要结合具体数据、算式的特点,合理选择算法,才能使计算变得更简便。
三、凑整,培养学生思维的开放性
凑整的方法不仅适用于数的四则运算、代数式的运算,也是解决几何问题的有效途径。如求图形的周长、面积时,可以通过平移、旋转、割补等方法对图形的某部分进行调整,把不规则的图形变成规则的图形,把不完整的图形变成完整的长方形或正方形,然后运用公式求出图形的周长或面积。
教学《长方形和正方形》时,笔者创设了一道凑整简算、寻找已知和所求条件的关联题。如图2,求组合图形的周长。
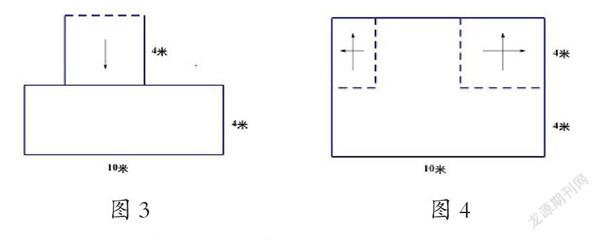
首先,笔者让学生观察图形,了解图形的特点和题中信息:图形是由两个不相等的长方形拼成的一个组合图形;已知大长方形的长和宽及小长方形一边的长;求组合图形的周长。接着,笔者引导学生根据题中信息厘清解题思路:要求组合图形的周长,就必须知道图形中各边的长度,而组合图形的上部分横着的三条线段的长度都是未知的,看似无法求出组合图形的周长,但通过仔细观察,可以发现上部分三条线段的和恰好是10米长的线段(长方形的对边相等)。笔者顺势设疑:怎样将这三条线段“凑”成一条线段呢?一名学生回答:将中间的一条线段向下平移,与另两条线段“凑”成一条线段。图中就含有一个长10米,宽4米的长方形(如图3),组合图形的周长就等于这个长方形的周长与2条4米的线段之和。另一名学生说:也可以把两边的线段向上平移,与中间一条线段“凑”成一条线段;再把竖着的两条线段分别向左右平移,与大长方形的宽“凑”成一条线段,组合图形就变成了一个长10米,宽“4+4=8”米的长方形(如图4),这个大长方形的周长,就是原组合图形的周长。
最后,笔者用动画演示平移线段的过程,让学生直观感受线段“凑整”的方法及原理。经过一系列引导,学生列出了不同的算式,如“(10+4)×2+4×2”“(10+4+4)×2”,并快速计算出组合图形的周长。
(作者单位:应城市杨岭镇中心小学)
责任编辑 张敏

