含缺陷的二维CuI光电性质的第一性原理计算

宋 娟， 贺 腾

(1.贵州大学 大数据与信息工程学院， 贵阳 550025； 2. 中国科学院半导体研究所 半导体材料科学重点实验室， 北京 100080)

1 引 言

自Geim等人利用物理剥离的方法从石墨上制备石墨烯后[1]，二维(2D)半导体因其独特的热力学特性，电学特性等成为当前研究热点，其中以石墨烯的研究最广泛，并且已将其用于高速电子器件、移动设备、DNA测序等领域[2-4]. 但石墨烯不存在带隙，这使其在光电子器件方面的应用受到限制，虽可通过吸附、掺杂等方式调控其带隙宽度，但又会影响石墨烯的其他物理特性. 考虑到石墨烯这一缺点，研究者将注意力转移到类石墨烯结构的二维材料上.

γ-CuI具有快离子导电性、较小的空穴有效质量等优点而引起人们的关注[5-7]，因此无论在生长研究上还是理论计算上的研究都进行了较多的研究[8-10]，如Hui Chen等人利用PBE探究了Zn，Cd，Hg掺入γ-CuI后的跃迁能，并发现Hg原子掺入γ-CuI后能提高其p型导电率[11]；Miso Lee等人探究了γ-CuI的电子结构以及光学性质并解释了其高空穴迁移率的内在机理[12]. 虽然目前对CuI晶体进行了大量的研究，但是对于二维γ-CuI而言，Kangkang Yao等于2018才首次利用物理气相沉淀法制备了高质量的2D CuI[13]，而在理论计算上还未有人对本征CuI单层进行理论计算，为进一步探究二维CuI的基本物性，因此展开对二维CuI光电特性的研究显得尤为重要. 此外，由于γ-CuI在制备的过程中会不可避免的出现本征缺陷，进而影响材料的性能，因此探究本征缺陷对二维CuI的结构、光电特性的影响极具研究意义. 因此本文利用第一性原理计算并分析了本征缺陷对二维CuI的光电特性，为实验上进一步探究2Dγ-CuI提供一定的理论参考.

2 计算模型与方法

体相γ-CuI属于闪锌矿结构，其晶格常数为:a=b=c=0.605 nm[14]，本文计算结构采用γ-CuI晶胞的(111)面，然后分别向a和b基矢方向分别扩胞四倍，得到(4×4)CuI单层，其中包括16个Cu原子和16个I原子，如图1(a)所示. 由于2D CuI中所有Cu原子以及所有I原子均为等价位点，因此在构建二维CuI的Cu或者I空位缺陷结构时只需将表面上的Cu原子或者I原子挖空即可. 本次计算基于从头算量子力学程序CASTEP软件完成，用GGA-PBE描述电子间的交换关联能，选用Cu和I的价电子组态分别为3d104s1和4d105s25p5，在计算过程中截断能设置为450 eV，k网格点密度设置为5×5×1，四个优化参数原子间最大相互作用力，原子间的最大位移收敛标准，作用在原子上最小的力以及自恰精度分别设置为0.02 GPa， 5.0×10-5nm，0.01 eV/Å以及5.0×10-6eV.

图1 计算结构图 (a) 本征CuI单层；(b) Cu缺陷的二维CuI；(c) I缺陷的二维CuI；(d) k空间的能带结构计算路径Fig. 1 Structure diagrams of calculation. (a) intrinsic 2D CuI structure; (b) Cu-deficient 2D CuI; (c) I-deficient 2D CuI; (d) energy band structure is calculated through the k-space path

3 结果与讨论

3.1 几何结构弛豫

本征2D CuI以及Cu和I缺陷时的优化参数如表1所示，其中包含了Cu-I键长以及体系的键布居. 表1中Cu-I的键长分为两类，分别为d1和d2(如图1所示)，d1表示非缺陷周围的Cu-I键长的平均值，d2代表与缺陷邻近的原子之间的键长. 从表1中可知本征2D CuI的Cu-I键长为2.5 Å；在Cu缺陷时，CuI单层中的Cu-I键长(d1)比本征CuI单层中的Cu-I键长略有增加，键长d2比本征CuI单层中的Cu-I键长小；在I缺陷时，CuI单层中Cu-I键长d1和d2均大于本征CuI单层中的Cu-I键长，这可能是由于缺陷周围的亚铜离子不稳定，然后导致亚铜离子相互靠近造成了对其他Cu-I键的拉伸作用. 键布居是衡量化学键的离子性和共价性特征的物理量，当键布居为0时，表明化学键为离子键，键布居越大，化学键的共价性越强. 从表1中可以看出本征CuI单层的键布居为0.43，在Cu缺陷以及I缺陷时，CuI单层的键布居均比本征CuI单层的键布居小，这表明Cu以及I缺陷的引入使二维CuI结构中Cu-I化学键的共价性减弱，离子性增强.

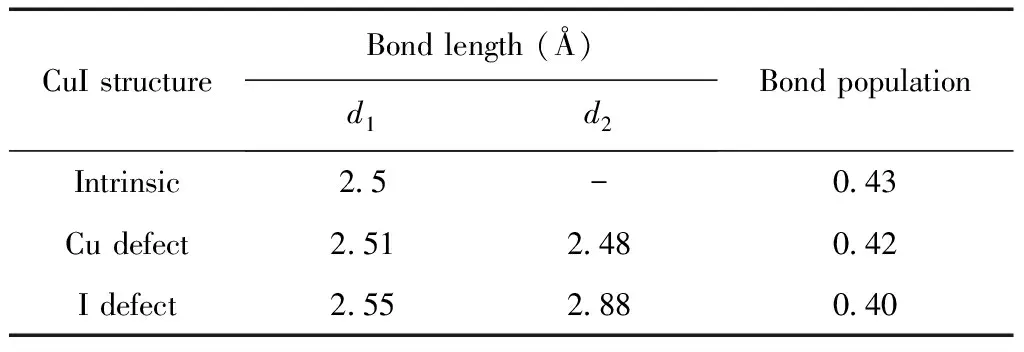
表1 本征二维CuI以及Cu和I缺陷时的键长以及键布居

3.2 电子结构

图2是本征CuI单层以及Cu和I缺陷时的能带图. 图2(a)为本征CuI单层的能带图，从图中可以看出其带隙值为1.56 eV，且导带底和价带顶均位于布里渊区的中心点，这表明2D CuI为直接带隙半导体. 结合态密度分析可知其导带主要来自于Cu-p以及I-s/p轨道sp2杂化的共同影响；其价带主要是来自于Cu-d以及I-p轨道的贡献. 图3(b)展示了Cu空位缺陷2D CuI的能带结构图，相比于本征CuI单层而言，其禁带宽度增大，为1.71 eV，这主要是由于导带底向高能端移动导致，这是由于Cu缺陷导致2D CuI的Ga-s/p向高能端导致，此外，Cu缺陷并未改变2D CuI的CBM和VBM的位置，它们均位于布里渊区的中心点. 图2(c)是2D CuI在I空位缺陷时的能带图，其禁带宽度为1.88 eV，其VBM和CBM分别位于布里渊区中心位置Γ和M点位置，这表明I空位缺陷时CuI单层为间接带隙半导体，价带电子吸收光子发生跃迁时必须吸收或者释放声子，且导带底所在的能级更加平缓，这表明I缺陷时2D CuI的电子有效质量增大，从而限制了电子的迁移率.

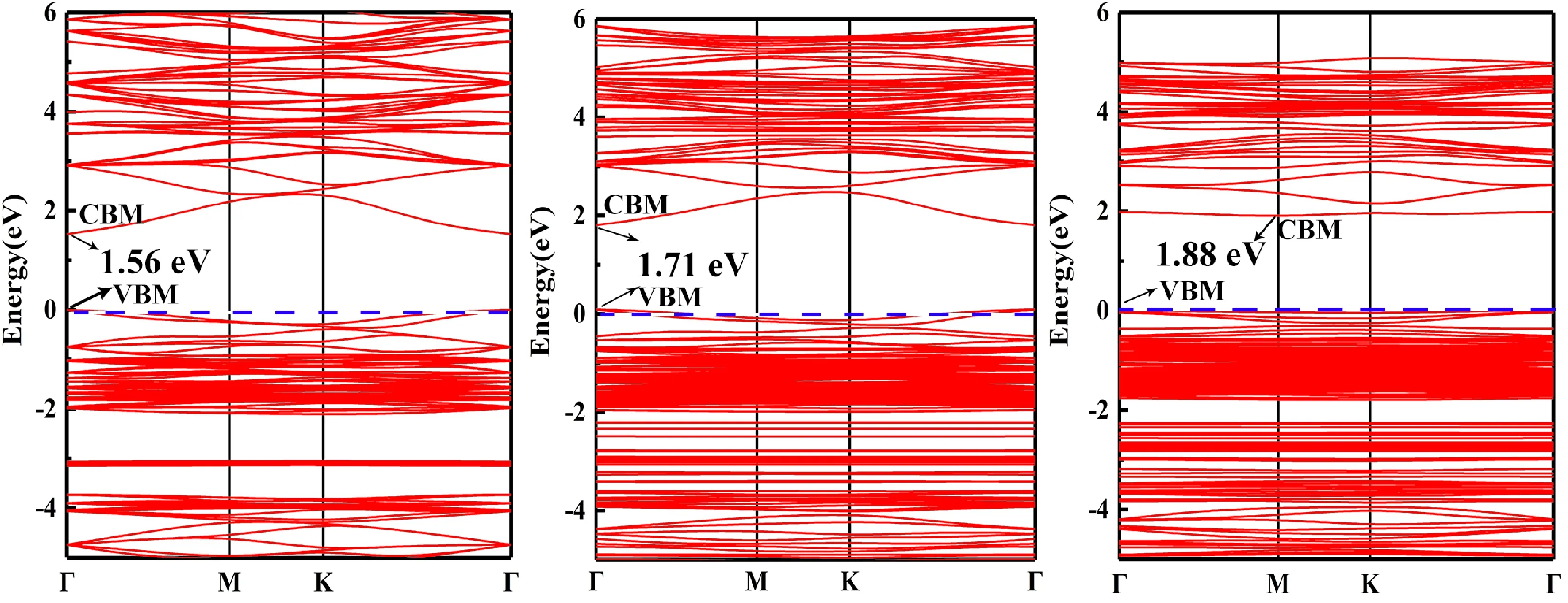
图2 能带结构 (a) 本征CuI单层结构；(b) Cu缺陷的2D CuI；(c) I缺陷的2D CuIFig. 2 Band structures. (a) intrinsic 2D CuI structure; (b) Cu-deficient 2D CuI; (c) I-deficient 2D CuI

图3是本征2D CuI以及Cu和I缺陷时2D CuI单层的总态密度和分波态密度. 图3(a)展示了本征CuI单层的态密度图，根据总态密度图可以将其分为三个能量范围进行分析，分别为-15 eV - -10 eV，-6 eV - 0 eV以及导带部分. 在能量范围为-15 eV- -10 eV内的总态密度主要由I-s态贡献；在-6 - 0 eV能量范围内的总态密度主要是来自于Cu-p态以及I-p态的贡献；导带部分的总态密度主要是来自于Cu-p以及I-s/p轨道sp2杂化的影响；图3(b)为2D CuI在Cu空位缺陷时的态密度图，相比于本征CuI结构而言主要有两个较为明显的变化，其一为在-12.5 eV附近新出现了一个较小的吸收峰，这主要是由于Cu缺陷时使2D CuI结构的I-s在该能量范围内出现一个较小的局域态组成；其二为-6 eV - 0 eV能量范围内总态密度的峰值均减小，这表明对应的峰值上的电子态减小，这主要是由于在-5 eV - 0 eV局域态内Cu-d态的峰值减小所导致；图3(c)为2D CuI在I空位缺陷时的态密度图，相比于本征CuI单层而言，在-15 eV - -10 eV和-6 eV- 0 eV范围内的总态密度的峰值有略微的减小，这主要是来自于I-s/p轨的影响.

3.4 光学性质

从图5(a)是2D CuI以及Cu和I缺陷时的复介电函数实部变化曲线. 从图中可以看出CuI单层的静态介电函数为2.47，然后随着入射光子能量的增加呈现先略微增加，介电函数虚部的变化较小，在7.5 eV能量附近达到最小值后随着能量的增加趋于不变. I缺陷时CuI单层的实部变化趋势和本征CuI单层的变化趋势一样. Cu缺陷时， CuI单层的静态介电函数为10.43，这表明Cu缺陷使CuI单层的耐高温特性增强，其后随着入射光子能量的增加急剧下降，在3 eV附近与本征CuI的虚部曲线的变化趋势一致.

复介电函数的虚部决定材料的光吸收特性，因此在分析材料的光学性质时对介电函数虚部的分析十分重要. 复介电函数虚部代表介质的损耗，它是由于分子的极化过程跟不上外场变化而引起. 图5(b)是介电函数虚部随入射光子能量的变化曲线. 可以看出未掺杂2D CuI的介电函数虚部有3个明显的特征峰，分别位于能量2.13 eV，4.64 eV，6.85 eV处，结合态密度图分析可以得知，其中A1峰主要来自于I-s态到Cu-d态电子的跃迁，A2以及A3峰主要来自I-p态到Cu-p态电子的跃迁. 引入I缺陷后，2D CuI只有A3对应的吸收峰存在，且该峰值相对于本征CuI单层的值略微减小；对于Cu缺陷的CuI单层而言，在光子能量为0时ε2(0)等于3.52，然后随着能量的增大迅速下降，在1.50 eV处达到极小值0.22，其后在3 eV附近与本征CuI单层的虚部曲线变化趋势相同.

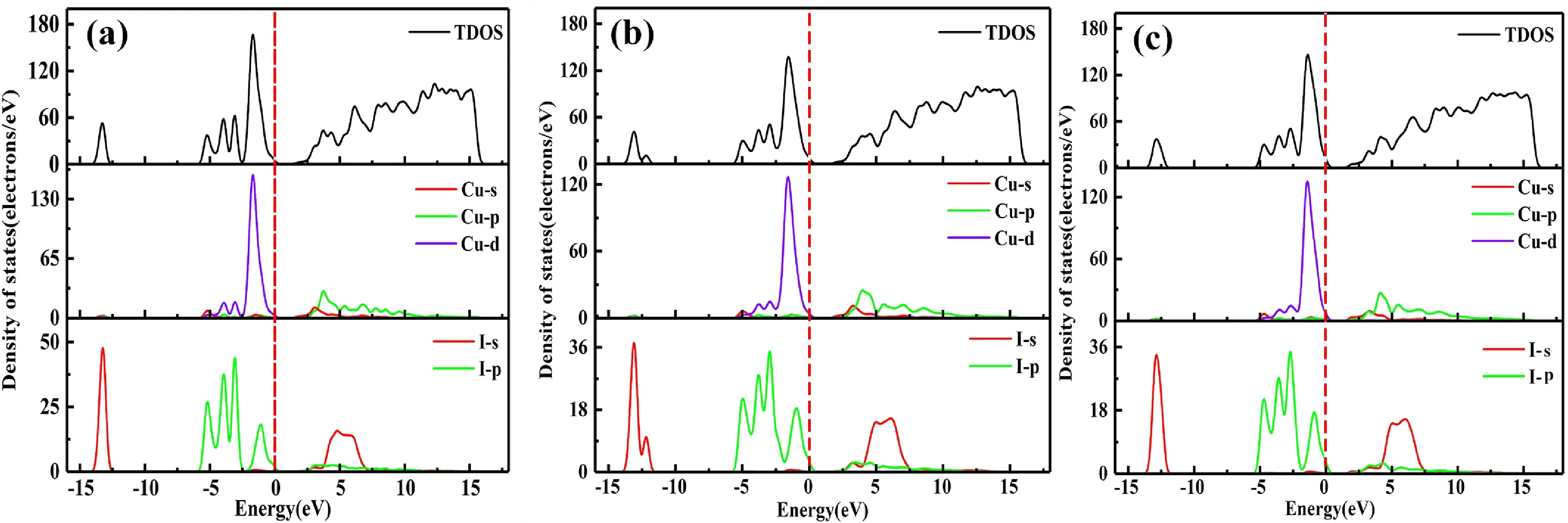
图3 总态密度与分波态密度 (a) 本征CuI单层结构；(b) Cu缺陷的2D CuI；(c) I缺陷的2D CuIFig. 3 Total densities of states and partial densities of states. (a) intrinsic 2D CuI structure; (b) Cu-deficient 2D CuI; (c) I-deficient 2D CuI

图4 CuI 单层以及Cu和I缺陷时的复介电函数(a)复介电函数实部；(b)复介电函数虚部Fig. 4 Complex dielectric functions of 2D CuI and 2D CuI with Cu and I defect; (a) the real part of complex dielectric; (b) the imaginary part of complex dielectric

4 总 结

本文基于密度泛函理论计算了2D CuI以及Cu和I缺陷时Cu和I原子之间的键长，布居电荷，能带结构，态密度以及复介电函数. 计算结果显示本征2D CuI的带隙为1.56 eV，为直接带隙半导体，Cu缺陷时2D CuI的带隙值增大至1.71 eV，这主要是由于导带底向高能端移动所导致；I缺陷时，2D CuI的带隙增大至1.88 eV，且使2D CuI变为间接带隙半导体材料，这主要是来自于Cu-s/p轨道的影响. 光学性质计算结果表明本征2D CuI的静介电函数为2.47， I缺陷的引入对2D CuI的静介电函数影响较小，但是在Cu缺陷后2D CuI的静介电函数急剧增大.