基于深度卷积神经网络的α-Fe晶界能预测

陈 村， 李六六， 彭 蕾， 时靖谊

(1.中国科学技术大学 核探测与核电子学国家重点实验室， 合肥 230026;2. 中国科学技术大学 核科学技术学院， 合肥 230027)

1 引 言

先进核反应堆结构材料铁素体/马氏体(F/M)钢在受到中子辐照后会产生大量的氦原子. 这些氦原子容易在结构钢中的晶界处聚集形成氦泡，从而导致材料脆化. 不同的晶界对氦泡诱导脆化的敏感程度是不同的[1]. “晶界工程”[2]通过控制和设计晶界来改进材料性能，首先需要获知结构钢中各晶界的性质. 晶界能作为晶界的主要特性之一，可在一定程度上衡量晶界的性质[3]. 获取晶界能的方法主要有理论推导、实验测量和模拟计算. 著名的Read-Shockley公式[4]基于理论推导得到了晶界能和取向差角之间的关系，但仅适用于小角度晶界. Hasson和Goux[5]通过实验测定了Al<100>和<110>对称倾斜晶界的晶界能随取向差角的变化规律,但该方法受到测量条件的限制，难以大范围运用. 因此，若能快速准确地获取晶界能，将为“晶界工程”提供便利，提高实验效率.

随着材料模拟技术的发展，更多地是基于分子动力学来研究晶界结构和晶界能，主要有考虑周期性边界条件的块状模型[6]和考虑非周期性边界的球形模型[7]. 分子动力学方法所要消耗的计算资源较大，并随晶界体系的增大而增加，难以满足“晶界工程”中计算大量晶界的需求. 因此，有少数研究者[8-10]尝试从数据科学的角度出发，在分子动力学模拟的基础上构造出合适的特征，并通过机器学习模型[11]对Al的晶界性能进行预测，但该方法的准确性受限于人为构造的特征，特征的好坏将直接影响预测效果. 由于模型信息量大，特征复杂，人工提取合适特征的难度较大，较难在大的倾斜角范围内得到应用.

近年来，深度学习[12]以更深层次的网络结构实现了自动提取特征的能力，在图像、语音、自然语言处理等方面均取得了非凡的成绩，也有研究者将其应用于生物蛋白质[13]、超高碳钢[14]和复合材料[15]中. 因此，本文主要针对F/M钢模拟α-Fe中常见的对称倾斜晶界，以中心对称参数和原子密度信息构建积累中心参数，并通过具有高效提取空间信息能力的深度卷积神经网络算法(CNN, Convolutional Neural Networks)[12]进行晶界能预测.

2 对称倾斜晶界库

针对α-Fe中常见的晶界，本文挑选出其中的具有一定倾斜轴(<100>和<110>)和倾斜角θ的对称倾斜晶界，利用LAMMPS软件[16]构造出稳定晶界构型并计算相应的晶界能. 先按重合位置点阵(CSL, Coincident Site Lattice)模型[17]建立两个具有一定取向的α-Fe晶粒，将其拼接后得到初步的双晶结构，两者交界面即为晶界平面. 同时为避免周期性边界条件导致的双晶界互相影响，遵循两晶界在晶界法向上间距大于12 nm的原则. 再应用晶界平面内平移(In-plane Translations) 和原子删除判据(Atom Deletion Criteria) 理论[18]枚举出大量可能的晶界构型. 然后在0 K下对每一个晶界构型进行静力学弛豫并对晶界附近原子进行微小的调整，筛选出能量最低的构型作为晶界结构. 其中铁原子间的相互作用通过Ackland等[19]发展的铁铁势函数Ackland04描述. 最后通过以下公式计算各晶界的晶界能大小：

(1)

其中γgb代表晶界能，Egb是含对称倾斜晶界双晶系统的势能，E1和E2分别是上下两个晶粒单独存在时的势能，A为晶界平面的大小.

结果如表1所示，一共构建了92个具有最低能量构型的α-Fe对称倾斜晶界,其中包括倾斜轴<100>的晶界结构32个和倾斜轴<110>的晶界结构60个.

3 深度学习模型与设计

预测晶界能的深度学习模型的整体流程如图1所示，在前一节建立的对称倾斜晶界库上以原子坐标为基础构建晶界特征参数(中心对称参数、积累中心对称参数). 再对完成特征构建的样本库进行分层抽样，划分为训练集和测试集. 通过卷积神经网络模型在数据增强后的训练集上进行学习、验证，并以测试集上预测的晶界能和模拟得到的晶界能间的相对差值来评估模型的真实预测效果.

3.1 特征参数构建

晶界平面附近的原子空间分布并不均匀，直接以空间结构进行学习的有效性极低. 考虑到块状晶界模型的周期性边界条件，本文以晶界原子的中心对称参数(CS, Centro-symmetry Parameter)[20]分布替代晶界结构达到了简化模型的作用. CS常用来衡量原子周围局部晶格的紊乱程度，在晶界处有较大的正值. 在对称倾斜晶界模型中，CS值仅与晶界平面法线方向(下文以y轴代表该方向)上的相对距离相关，相同的晶界在y轴上具有相同的CS相对分布. 因此，通过该参数可以将三维的空间信息简化到二维的相对分布，从而降低计算复杂度，相比于传统机器学习方法构造的特征也更为简便，其计算公式[20]如下：

(2)

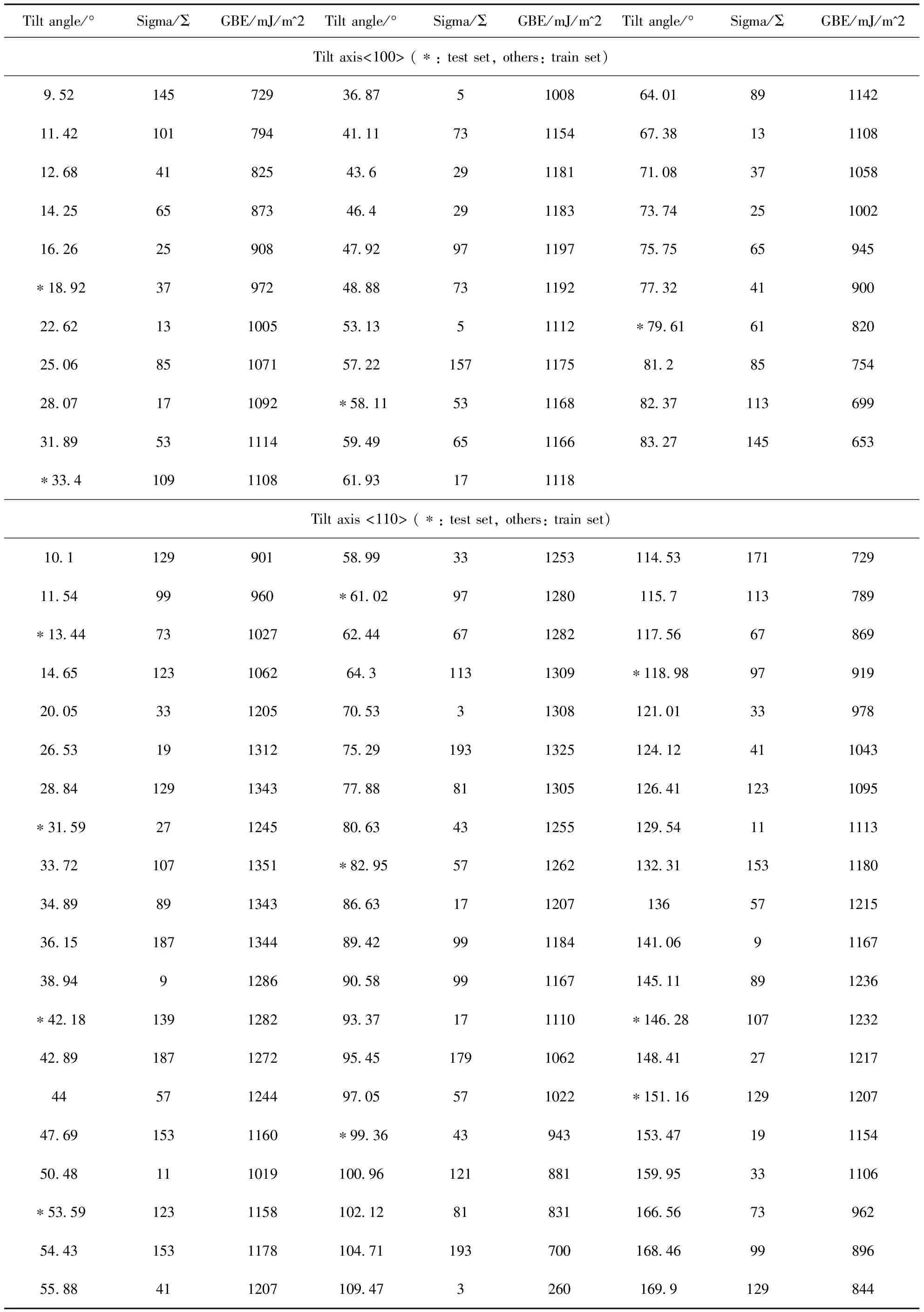
表1 α-Fe对称倾斜晶界各晶界参数

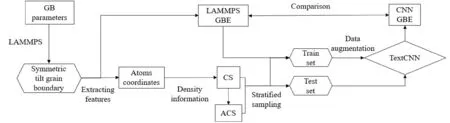
图1 预测晶界能流程图Fig. 1 Flow chart of grain boundary energy prediction

同时，考虑到不同倾斜角的晶界在y方向上的原子密度是不同的，本文利用伊番科尼可夫核函数(Epanechnikov Kernel)融合进原子密度信息构造了积累中心对称参数(ACS, 如图2绿色线所示). 最终对(-20 Å, 20 Å)区间内的CS和ACS分布分别等间隔地取401个值作为模型的输入特征.

图2 <110>倾斜轴的Σ9对称倾斜晶界上中心对称参数、连续的中心对称参数以及积累中心对称参数随y轴坐标的分布图Fig. 2 For a Σ9 symmetric tilt grain boundary with a tilt axis of <110>, the distribution of centro-symmetry parameter, continuous centro-symmetry parameter and accumulate centro-symmetry parameter along Y coordinate

3.2 卷积神经网络模型

本文以适合一维卷积的TextCNN模型[21]为基础，通过PYTORCH 1.5.1搭建了卷积神经网络模型，整个模型的参数量在1.7*105左右. 如图3所示，模型主要由卷积层、池化层(Pooling)和两层全连接层(FCN)组成. 卷积层通过卷积核的滑动进行卷积计算，本文使用了多个不同尺寸的卷积核，单个尺寸卷积核设置为k(50、100、150、200)个，卷积计算后通过修正线性单元(ReLU)[11]引入非线性. 池化层作为一种下采样操作主要用于降维，对每一组特征采用最大值池化中的Chunk-Max-Pooling[21]筛选出局部最大的4个值. 最后将池化层输出的特征按序拼接后展平输入隐藏层单元为(64,16)的全连接层，并以0.5的概率暂时丢弃一定数量的神经元，防止网络出现过拟合现象. 使该模型在训练集上循环训练1000个周期，并通过平滑的L1损失[11]更新模型的参数. 参数的更新算法采用Adam算法[22]，参数更新的学习率对于ACS特征设置为3 e-4，对于CS特征前100个周期设置为1 e-4，之后为1 e-5.

4 预测结果与分析

依据表1的对称倾斜晶界库统计了晶界能随倾斜角的分布，如图4所示. 这与Yasushi S等[23]构建的体心立方晶体对称倾斜晶界的晶界能随倾斜角的分布相接近. 从图中可见，相邻倾斜角的晶界能较为接近，因此，本文通过按倾斜角分层抽样的方法划分了训练集和测试集. 首先，统计晶界在各倾斜角区间的样本个数，尽可能地保留稀疏区间的样本作为训练集，最终以28个<100>倾斜轴晶界和50个<110>倾斜轴晶界分别作为原始训练集.

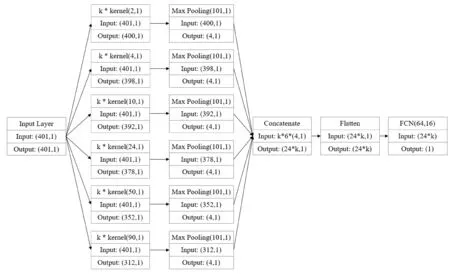
图3 卷积神经网络模型框架图Fig. 3 Illustration of convolutional neural networks framework

图4 α-Fe中倾斜轴为(a)<100>和(b)<110>的对称倾斜晶界倾斜角与晶界能关系图Fig. 4 Grain boundary energies of the symmetric tilt boundaries in α-Fe as a function of tilt angle for the tilt axes of (a) <100> and (b) <110>

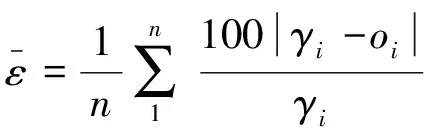
(3)

式中γi为分子动力学计算的目标晶界能，oi为预测晶界能，n为测试样本数.

4.1 晶界能预测结果

不同卷积核尺寸的模型预测晶界能的平均相对误差随训练周期的变化如图5(a)所示，这里同尺寸卷积核的个数设置为100个. 可以看到，平均相对误差随循环周期增加逐渐下降，在1000个周期时均能趋于平稳，并未出现再次上升的情况，这说明模型未出现过拟合现象. 其中ACS特征在参数更新的学习率高于CS特征的情况下误差下降趋势仍更缓慢，这在一定程度上反映了ACS特征相比于CS特征更加地复杂，难以学习. 在所有模型中，ACS特征在卷积核尺寸为(2,4,10,24,50,90)的网络中取得了最低的平均相对误差1.74%，而同模型CS特征的平均相对误差仅为4.17%，增大了2.43%. 在其余同卷积核尺寸模型中，ACS特征模型的平均相对误差均低于CS特征模型. 进一步分析同特征在不同尺寸卷积核模型上的表现：ACS特征在(2,4)、(2,4,10,24)、(2,4,10,24,50,90)卷积核模型上的平均相对误差依次为5.08%、3.90%和1.74%，CS特征为6.31%、5.94%和4.17%. 通过比较差值发现，无论是ACS特征还是CS特征，更大尺寸的卷积核使模型平均相对误差下降更明显. 而由于输入参数规模的限制，进一步设置更大尺寸的卷积核较为困难，通过增加同尺寸卷积核的个数亦能得到更大规模的卷积网络模型，因此在图5(b)中以卷积核尺寸为(2,4,10,24,50,90)的模型作为基础模型，通过改变单个尺寸卷积核的个数，比较了更大规模网络的平均相对误差. 结果表明，在单尺寸卷积核个数为100的模型上平均相对误差是最低的，稳定在2%左右，最低可达到1.74%.

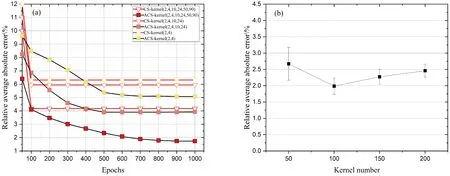
图5 (a)不同模型预测晶界能的平均相对误差随循环周期变化 (b) 平均相对误差随卷积核个数的变化Fig. 5 (a)Relative average absolute errors (%) of predicted grain boundary energies of the different CNNs. (b) Relative average absolute errors (%) of the different convolutional kernel numbers

针对具有最低平均相对误差的卷积核尺寸为(2,4,10,24,50,90)、同尺寸卷积核个数为100的模型，比较了分子动力学计算的晶界能和模型预测的晶界能间的差距. 如图6(a-b)所示，CS特征模型在测试集上的平均相对误差(4.17%)高于ACS特征模型(1.74%)，样本分布更为离散，出现较大相对误差的可能性也更大. 经图6(c-d)统计，测试集上，ACS特征模型的最大相对误差小于6%，而CS特征模型则达到了10%. 由于测试集样本较少，在图中一并统计了原始训练集上的相对误差样本分布，可见ACS特征模型上的分布也更为集中. 综合以上结果，ACS特征模型相比于CS特征模型在预测晶界能的任务中有更大的优势. 相比于文献8以机器学习方法在Al的非对称倾斜晶界上预测晶界能取得的结果(晶界能在200至600 mJ/m2范围内的平均绝对值误差为11.35 mJ/m2)，本文在更广倾斜角范围的对称倾斜晶界上取得了相当的结果.

通过输出TextCNN最后一层网络的权值可以得到经该模型加工后的16维晶界特征(vi)和晶界能(GBE)间的定量关系：

GBE=0.23v1-0.28v2+0.19v3+0.28v4-

0.26v5+0.27v6+0.14v7-0.14v8-

0.15v9-0.12v10-0.21v11-0.30v12-

0.16v13+0.19v14-0.13v15+0.21v16

(4)

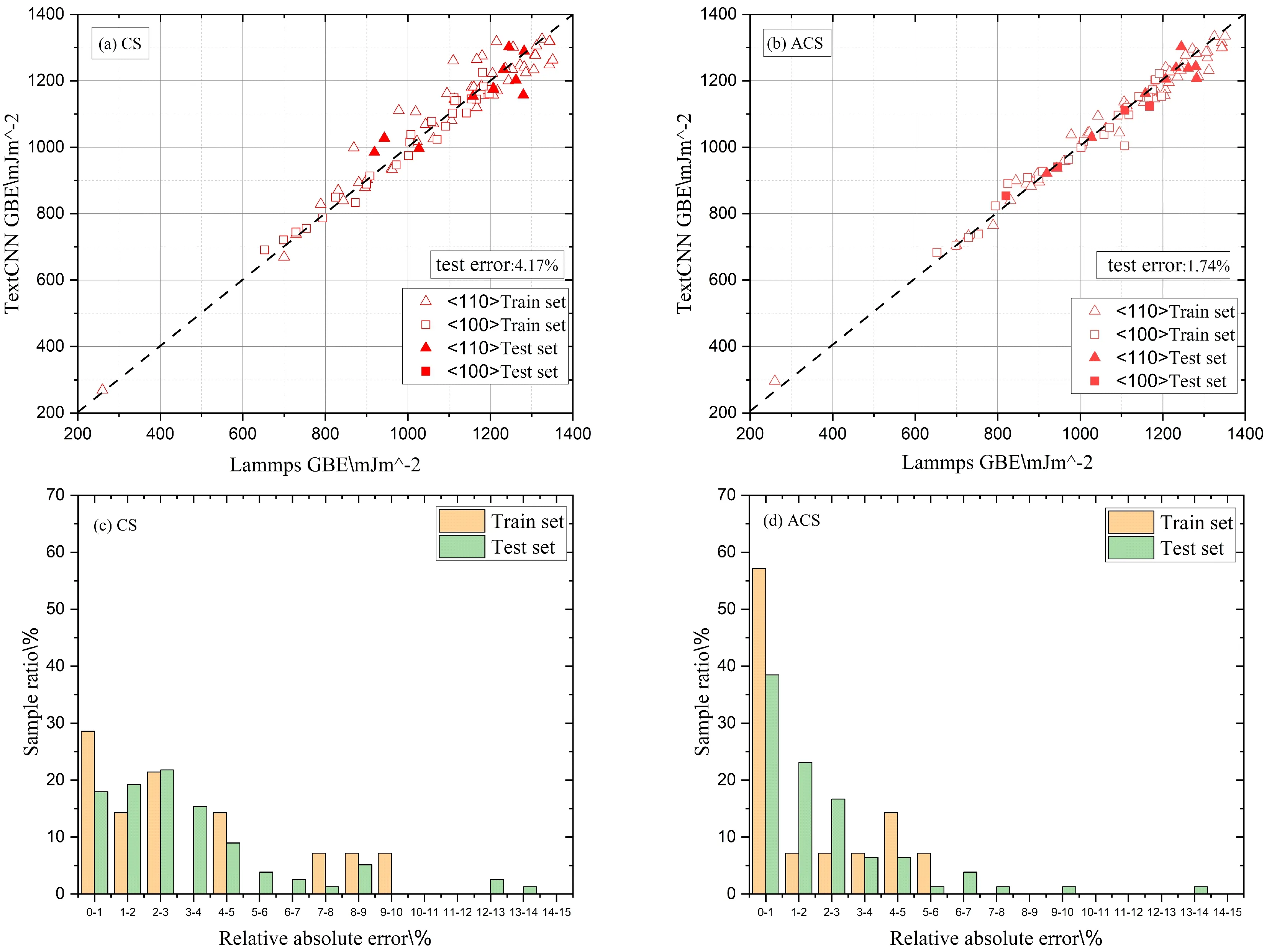
图6 (a-b)所有样本集上原始晶界能和预测晶界能对比图，(c-d)预测结果统计分布图.Fig. 6 (a-b) The original GB energies are compared with the predicted GB energies in the whole set; (c-d) Statistical result of network prediction

4.2 分层抽样和数据增强的影响

为了进一步确认按倾斜角分层抽样对模型预测能力的影响是正向的，在部分的数据集上分别以CS和ACS作为晶界特征在同样的模型上比较了三种抽样方式(按倾斜轴分层抽样、随机抽样、不均匀抽样)对模型预测能力的影响. 其中，不均匀抽样是只选择了倾斜角较大的样本. 在同样的测试集上计算了晶界能的平均相对误差，结果如图7所示，不论是ACS特征还是CS特征，分层抽样得到的平均相对误差均是最小的，随机抽样次之，不均匀抽样最大. 这表明了不同倾斜角的对称倾斜晶界的晶界结构是有一定的差异的，仅使用一定倾斜角范围内的晶界将导致样本在特征空间分布不均匀，易发生过拟合的情况，在更大倾斜角范围内的晶界上预测结果较差. 因而通过按倾斜角分层抽样的途径，能让训练样本空间分布得更加均匀，使模型在测试集晶界上能有更准确的预测结果.

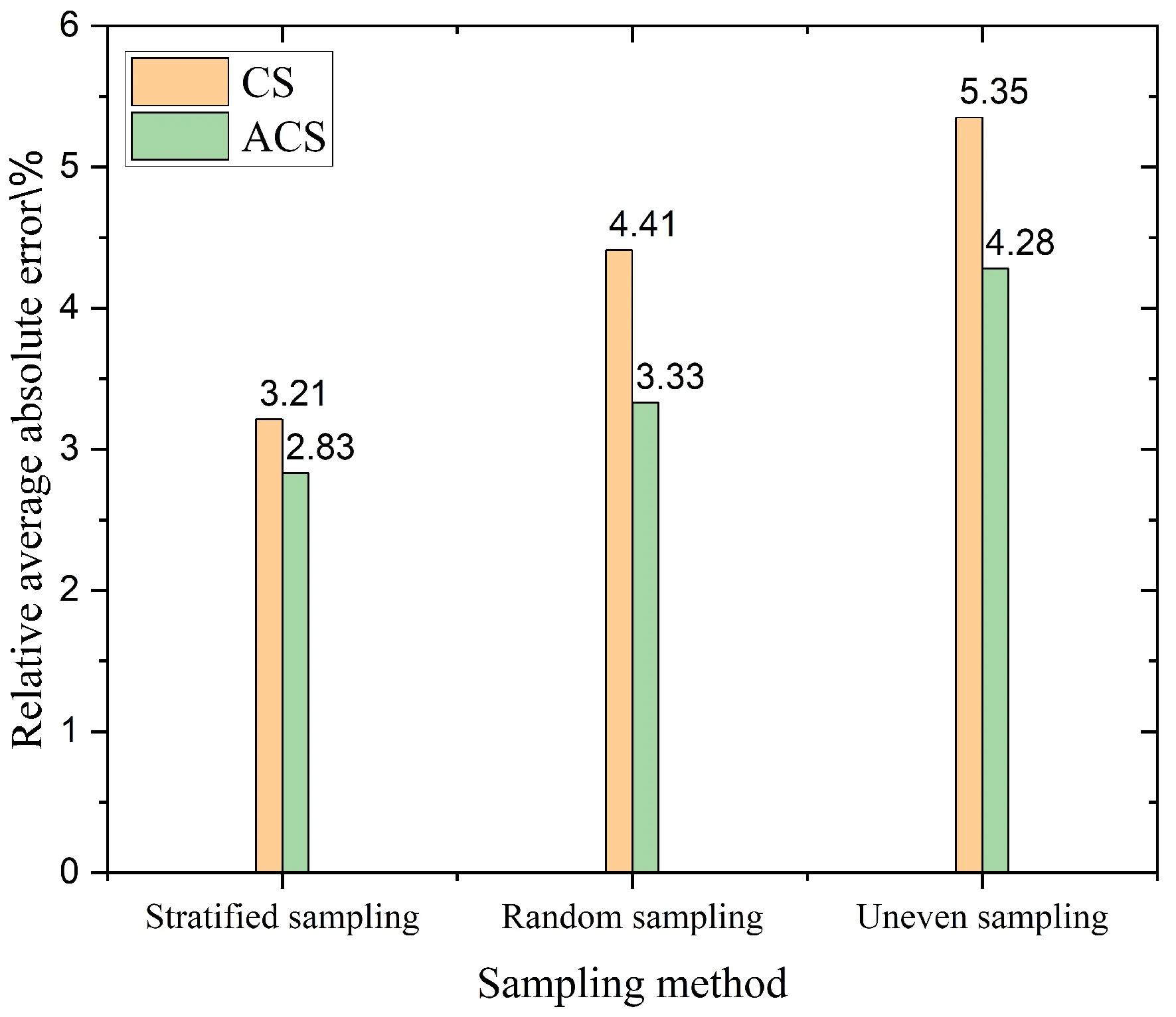
图7 不同训练集采样方法在CNN模型上预测晶界能平均相对误差的变化Fig. 7 Relative average absolute errors (%) of predicted grain boundary energies of the CNN varies with the different sampling methods

如图8所示，以同一模型为基础，对同一训练集进行数据增强，通过改变增强样本的个数在相同测试集上比较了平均相对误差的变化. 结果表明，相较于未进行数据增强的模型，合理引入增强样本能够降低模型预测晶界能的平均相对误差，而随着增强样本个数的增多，平均相对误差在增强样本个数为65左右时达到了最低点，随后出现了一定的上升. 以此可见，数据增强在一定范围内能够合理地增加训练集的个数，提高模型的鲁棒性，但随着平移尺度的加大和增强样本个数的增多，对模型引入了一些负面的噪声，改变了训练数据的主要特征分布，导致模型的预测精度产生了一定的下降，类似的结论在文献[25]中也有体现. 因此，选择合适的增强尺度和增强样本个数对提升模型的预测性能是十分重要的.

图8 不同数据增强样本个数下预测晶界能平均相对误差的变化Fig. 8 Relative average absolute errors (%) of predicted grain boundary energies varies with the augmented sample numbers

5 结 论

本文基于卷积神经网络TextCNN结构，在α-Fe的<100>和<110>倾斜轴的对称倾斜晶界上建立了晶界能预测模型. 以融合原子密度信息的积累中心对称参数作为晶界特征，通过按倾斜角分层抽样和“翻转平移”的数据增强方法进一步提升了模型的效果. 测试集结果表明，该方法预测晶界能的平均相对误差小于1.75%. 通过该方法，本文在深度学习的模型基础上建立了晶界结构和晶界能之间的连接，这种连接方法同样可用于预测其他晶界性能，为进一步研究F/M钢晶界工程提供了支撑.