囚禁离子非线性Rabi模型量子场熵演化特性

鲁恩民， 王中结

(安徽师范大学 物理与电子信息学院， 芜湖 241000)

1 引 言

量子纠缠一直是量子通信[1]、量子密码[2]、量子隐形传态[3]等方向的核心内容. 量子纠缠一词首次出现是在1935年薛定谔发表的猫态一文中[4]，经过后人对于量子世界逐渐探索，量子纠缠才真正的被人们所接受和理解. 1982年法国Aspect实验小组关于检验Bell不等式的实验[5],宣告着人们对于量子纠缠的认识从经典论转向量子力学范畴. 对于量子纠缠的研究成果开始爆发式的涌现，首先是在量子判据方面，Peres[6]、Schlienz[7]、Keller[8]等人分别给出了不同的解释，其次许许多多不同的纠缠度量方法被提出，其中Phonenix和Knight等人就将熵理论应用于部分纠缠度量中[9,10]，因其既可以分析场与原子之间经典与非经典的关联程度，又可以分析场与原子之间纠缠特性，所以近些年来，利用量子场熵来度量系统与光场之间纠缠度的研究取得了令人欣喜的结果. 2017年 Arturo Zǘniga-Segundo等人证明了混合态的原子与场的相互作用可以计算出两倍于崩溃时间的场熵[11]. 2018年刘堂昆等人介绍了如何通过量子场熵来计算相干态光场与双量子态的两个原子相互作用的纠缠度等[12]. 2019年Jorge A. Anaya-Contreras等人研究了用Araki-Lieb不等式从原子熵来计算场熵[13].

本文所研究的量子Rabi模型在量子信息方面是靠量子模拟来实现，主要的量子模拟平台有超导电路[14]，超冷原子气体[15]，和囚禁离子平台[16]等. 本文首次将Von-Neumann量子约化熵理论引入到囚禁离子非线性Rabi模型量子场熵演化特性的研究中，间接的研究囚禁离子与光场之间的量子纠缠，并借助计算机的模拟，给出Lamb-Dicke参数和初始平均光子数对量子纠缠的影响.

2 模型及其解

我们考虑了一个被囚禁在谐波势阱中的离子，它与失谐的一阶红、蓝边带光场相互作用，产生相应的失谐量，即光学RWA读出后系统的哈密顿量:

(1)

其中，δ1=ω1-ωa+kν,δ2=ω2-ωa-kν,ωa是两能级跃迁频率，ω1,2是驱动激光的频率，ν是囚禁势频率，σz是与这个两能级系统相关的泡利矩阵，σ+是原子上升算符，Ω是拉比频率. 如果我们应用振动的旋转波近似，我们得到

(2)

式中

(3)

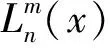
(4)

如果选择k=2，我们可以得到如下的双光子非线性Rabi模型

(5)

假设在初始时间原子处于激发态|e>，光场处于相干态|α>，系统的初始状态为：

(6)

系统在任何时刻的波矢可以表示为：

(7)

将(7)代入由单光子非线性拉比模型的哈密顿量(4)或双光子非线性拉比模型的哈密顿量(5)所决定的薛定谔方程，得到与和有关的相应微分方程.

3 光场与囚禁离子之间的量子纠缠演化特性

由(5)式可以得到相互作用系统的密度算符ρ(t)=|ψΙ(t)〉〈ψΙ(t)|，根据Von-Neumann量子约化熵理论，激光场的约化密度矩阵为：

ρL(t)=Triρ(t)=Tri{|ψΙ(t)><ψΙ(t)}

(8)

采用文献[13]中的处理方法，可以得到光场约化密度矩阵的本征值为

(9)

(10)

从而我们可以得到光场的Von-Neumann量子约化熵为

(11)

4.1 Lamb-Dicke参数对量子纠缠的影响

我们取|α|2=20，Lamb-Dicke参数取不同值时，求解方程后我们可以做出数值计算，得到量子场熵随标度时间的演化曲线如图一所示.

图1 Lamb-Dicke参数取不同值时，量子场熵随标度时间的演化曲线(a)η=0.5;(b) η=0.6;(c) η=0.7;(d) η=0.8Fig. 1 Evolution curves of quantum field entropy with scaling time when Lamb-Dicke parameter takes different values(a)η=0.5;(b) η=0.6;(c) η=0.7;(d) η=0.8

图1我们给出了|α|2=20时，Lamb-Dicke参数η取不同值时，量子场熵随标度时间的演化曲线，我们可以看出Lamb-Dicke参数η影响着量子场熵演化曲线的周期性，Lamb-Dicke参数η较大时，周期性越来越明显，这说明了Lamb-Dicke参数η对量子场熵起到了一定的调制作用，随着Lamb-Dicke参数η的不断增大，我们发现存到达某极值后调制效果达到最大随后调制效果开始减弱. 其次量子场熵演化曲线的平均值是先变小后变大，曲线的振荡幅度先增大而后减小，振荡的频率越来越慢. 这说明了随着Lamb-Dicke参数η的不断增大，囚禁离子与驻波激光场之间量子纠缠强度先减弱后增强.

4.2 初始平均光子数对量子纠缠的影响

我们取Lamb-Dicke参数η=0.7. 初始平均光子数取不同值时，我们可以做出数值计算，得到量子场熵随标度时间的演化曲线如图二所示.

图2我们可以给出了当Lamb-Dicke参数η=0.7时，量子场熵与平均光子数之间的关系，可以看出场熵的演化具有明显的振荡性，其次随着初始平均光子数的增大，量子场熵的平均值是先减小后增大. 其振荡频率和振荡幅度都是随着初始平均光子数的增大，先减小后增大. 这也就是说，随着初始平均光子数的增大，囚禁离子与驻波激光场之间量子纠缠的程度先减弱后增强.

5 双光子Rabi模型中场熵演化

5.1 Lamb-Dicke参数对量子纠缠的影响

在这一章节的研究中我们取|α|2=20，改变Lamb-Dicke参数的取值，来研究Lamb-Dicke参数对于量子纠缠曲线的影响，得到的量子场熵随标度时间的演化曲线如图四所示：

从图中我们可以看出双光子Rabi模型场熵的演化曲线有明显的周期性，这说明原子与光场的纠缠呈现周期性的变化并且随着Lamb-Dicke参数η的增大，场熵的周期性在逐渐消失，当Lamb-Dicke参数η较小时出现了周期性的纠缠和退纠缠即退耦现象，随着Lamb-Dicke参数η的不断增大，场熵的退纠缠现象消失. 另一方面，量子场熵演化曲线的平均值在逐渐增加，振荡的频率越来越快. 这说明了随着Lamb-Dicke参数η的不断增大，囚禁离子与驻波激光场之间量子纠缠强度在逐渐增强. 从中我们可以看出Lamb-Dicke参数η对于场熵的演化曲线有明显的调制作用.

图2 初始平均光子数取不同值时，量子场熵随标度时间的演化曲线Fig. 2 The evolution curves of quantum field entropy with scaling time when the initial average photon number is

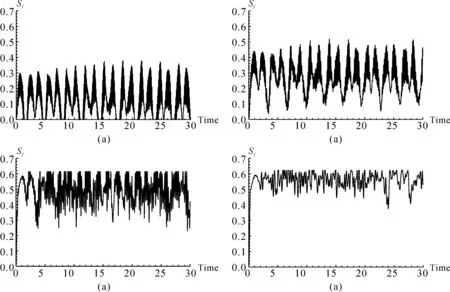
图3 Lamb-Dicke参数取不同值时，量子场熵随标度时间的演化曲线(a)η=0.25;(b) η=0.30;(c) η=0.35;(d) η=0.40.Fig. 3 Evolution curves of quantum field entropy with scaling time when Lamb-Dicke parameter takes different values(a)η=0.25;(b) η=0.30;(c) η=0.35;(d) η=0.40.

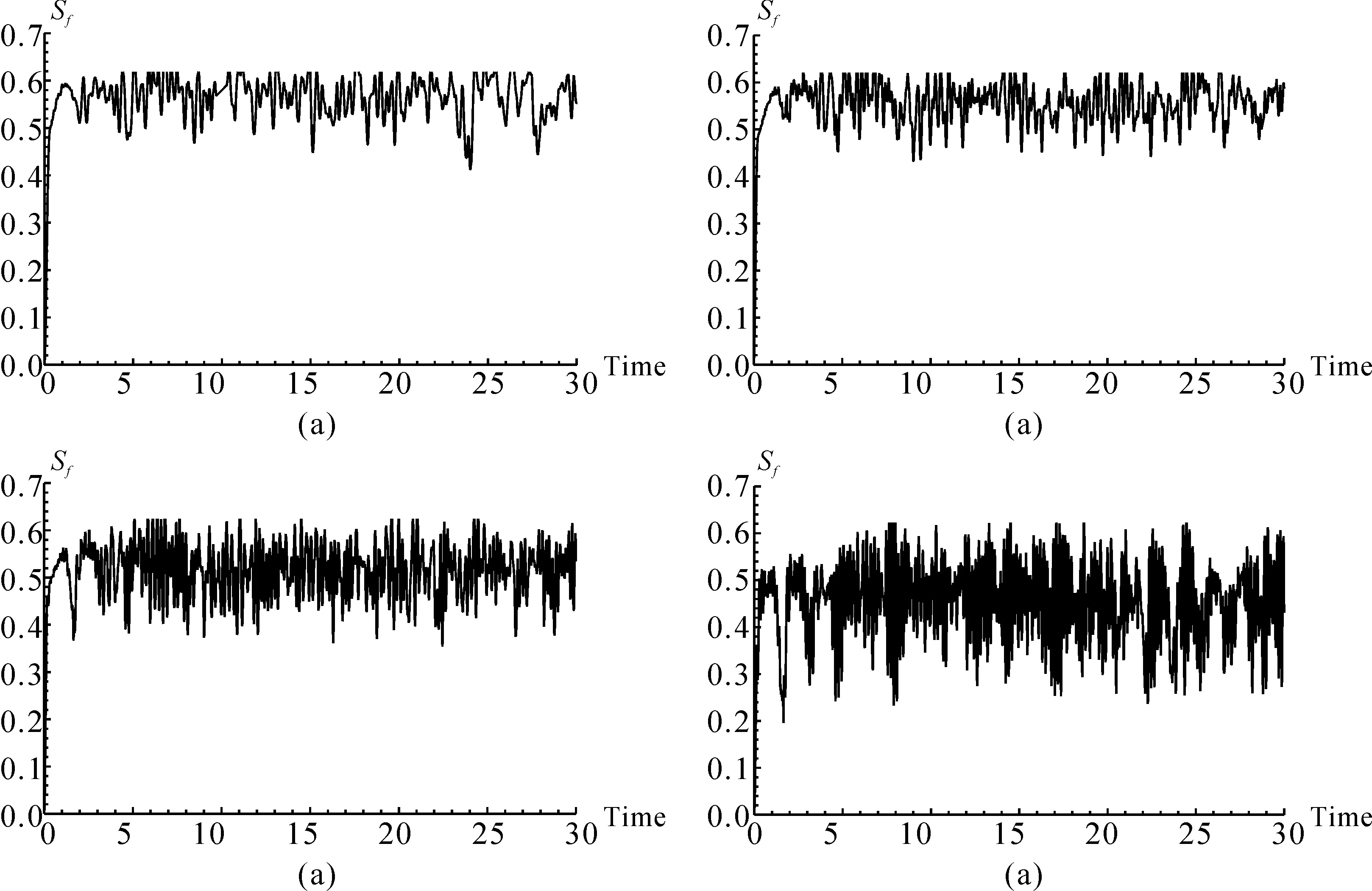
图4 初始平均光子数取不同值时，量子场熵随标度时间的演化曲线Fig. 4 The evolution curves of quantum field entropy with scaling time when the initial average photon number is

5.2 初始平均光子数对量子纠缠的影响

在这一节中我们取Lamb-Dicke参数η=0.40，改变初始平均光子数，来探究初始平均光子数对于量子纠缠的影响.

从图5中我们可以看出，场熵的演化曲线具有周期性，这说明光场与原子的纠缠存在周期性，随着初始平均光子数的增大，量子场熵的平均值逐渐减小，振荡幅度略有增加，振荡频率加快. 这也就是说明，随着初始平均光子数的增大，囚禁离子与驻波激光场之间量子纠缠的程度越来越弱.

6 结 论

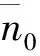
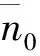
根据上述囚禁离子与驻波激光场之间的量子纠缠特性，我们可以选取适当的Lamb-Dicke参数η和使得初始选取恰当的光子数来制备纠缠态或纯态，还可以利用这些演化特性构建有用的量子逻辑门等.