非线性两能级系统中的Landau-Zener-Coulomb跃迁
豆福全, 胡 丹, 孙建安
(西北师范大学 物理与电子工程学院, 兰州 730070)
1 引 言
量子非绝热跃迁作为量子力学中的一种基本现象, 涉及到化学反应系统、核物理系统和超冷原子系统等多个领域[1-7]. 长期以来, 人们为了研究量子非绝热跃迁这一现象, 引进了众多模型, 其中多通道Landau-Zener-Coulomb模型作为可精确求解的模型之一, 是由Sinitsyn于2013年提出. 不同于其它模型, 在该模型中, 能级之一是根据库仑定律衰减的[8], 而其它能级则是随时间线性变化. 随后,Sinitsyn团队基于该模型对量子非绝热跃迁进行了大量的研究, 得到了一系列结果, 包括跃迁概率的解析表达式, 跃迁过程中的反直觉行为以及振荡现象等[8, 9]. 此外, 该模型在Rydberg原子和分子碰撞中也有着重要应用[10-15].
实际上对于真实的物理系统, 特别是超冷原子系统, 往往由于存在粒子间相互作用而使系统具有非线性[16]. 这些非线性会使物理系统出现一系列新奇现象. 近年来, 许多学者对非线性系统, 特别是对非线性系统的跃迁动力学进行了广泛地研究. 如非线性Landau-Zener隧穿[17-22]、非线性Rosen-Zener跃迁[23, 24]和非线性Demkov-Kunike跃迁[25]等. 而对于Landau-Zener-Coulomb模型, 如果系统中存在粒子间相互作用, 其跃迁动力学仍不清楚.
本文研究了非线性两能级系统中的Landau-Zener-Coulomb跃迁动力学. 在非绝热条件下, 通过将能级的斜率分为为正和为负两种情况, 讨论了粒子间相互作用对Landau-Zener-Coulomb跃迁动力学的影响, 发现当能级的斜率为正时, 非线性会抑制非绝热跃迁, 且非线性强度越大, 两能级间的非绝热跃迁越难发生. 而为负时, 弱非线性会促进非绝热跃迁, 对于强非线性情况, 跃迁概率会出现振荡. 随着非线性强度的增大, 振荡幅度逐渐减小, 能级间的非绝热跃迁受到抑制.
2 模型与能级
非线性两能级系统的Landau-Zener-Coulomb跃迁可以由下面无量纲化的薛定谔方程描述:
(1)
哈密顿量为

(2)
其中a,b是|0〉态和|1〉态的概率幅, 系统的总概率|a|2+|b|2=1.k是|0〉态的能级曲率,β为|1〉态的能级斜率,g和c分别是两个能级之间的耦合强度和描述粒子间的相互作用的非线性参数.
由于系统是从τ→0到τ=+∞演化, 假设初始时刻τ→0时系统完全制备在|0〉态上. 定义跃迁概率为P0→1=|b(+∞)|2. 则线性情况下(c=0)跃迁概率如下所示[8]
(3)
(4)
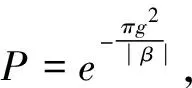
(5)
通过数值求解(5)式, 得到如图1所示的能级结构图. 其中初始态在上能级上, 随着非线性的出现, 能级结构发生了改变. 当能级的斜率为正时, 如图1(a)所示, 随着非线性强度的逐渐增大, 系统的下能级出现了环状结构, 并随非线性强度的逐渐增大而扩大. 而当能级的斜率为负时, 如图1(b)所示, 非线性相互作用也会使系统的能级结构发生改变, 当非线性强度增大到超过某个临界值时上能级上出现了环状结构, 且随着非线性强度的增大会变大.
为获得粒子间相互作用的临界值并分析系统中出现的动力学性质,可通过正则变换将非线性两能级系统转化为经典哈密顿系统[18]. 其中a=|a|eiθa,b=|b|eiθb, 引入布居数差s=|b|2-|a|2和相对相位差θ=θb-θa, 得到系统的经典哈密顿量:
(6)
θ=0,π,
(7)
(8).

相互作用临界值满足:

图1 (a)k2=0.7,β=1.0,g=0.3时不同非线性强度下的能级结构; (b)k2=0.2,β=-1.0, g=0.3时不同非线性强度下的能级结构.Fig. 1 (a) Energy levels for different nonlinear strengths with k2=0.7,β=1.0,g=0.3; (b) Energy levels for different nonlinear strengths with k2=0.2,β=-1.0,g=0.3.
(9)
(10)
3 Landau-Zener-Coulomb跃迁动力学
本部分将采用4-5阶龙格-库塔法数值计算能级斜率分别为正和为负两种情况下两能级系统中的跃迁动力学. 数值计算中时间取τ=0.0001到τ=800.
3. 1 能级斜率为正的情形
首先探究跃迁动力学的一些基本规律. 数值结果如图2-4所示, 图2展示了不同非线性强度下跃迁概率随演化时间的变化, 图中取k2=0.7,β=1.0,g=0.3. 可以看出随着时间的增大, 跃迁概率会稳定在一个固定值, 且随着非线性强度的增大持续降低, 能级间的非绝热跃迁受到抑制. 图3展示了不同非线性强度下跃迁概率随耦合强度、能级斜率以及能级曲率平方变化. 其中棕色方块线表示c=0.0的解析结果. 图4展示了跃迁概率随非线性强度的变化. 我们发现非线性总是抑制两能级间的非绝热跃迁, 且非线性强度越大, 两能级间的非绝热跃迁越难发生.
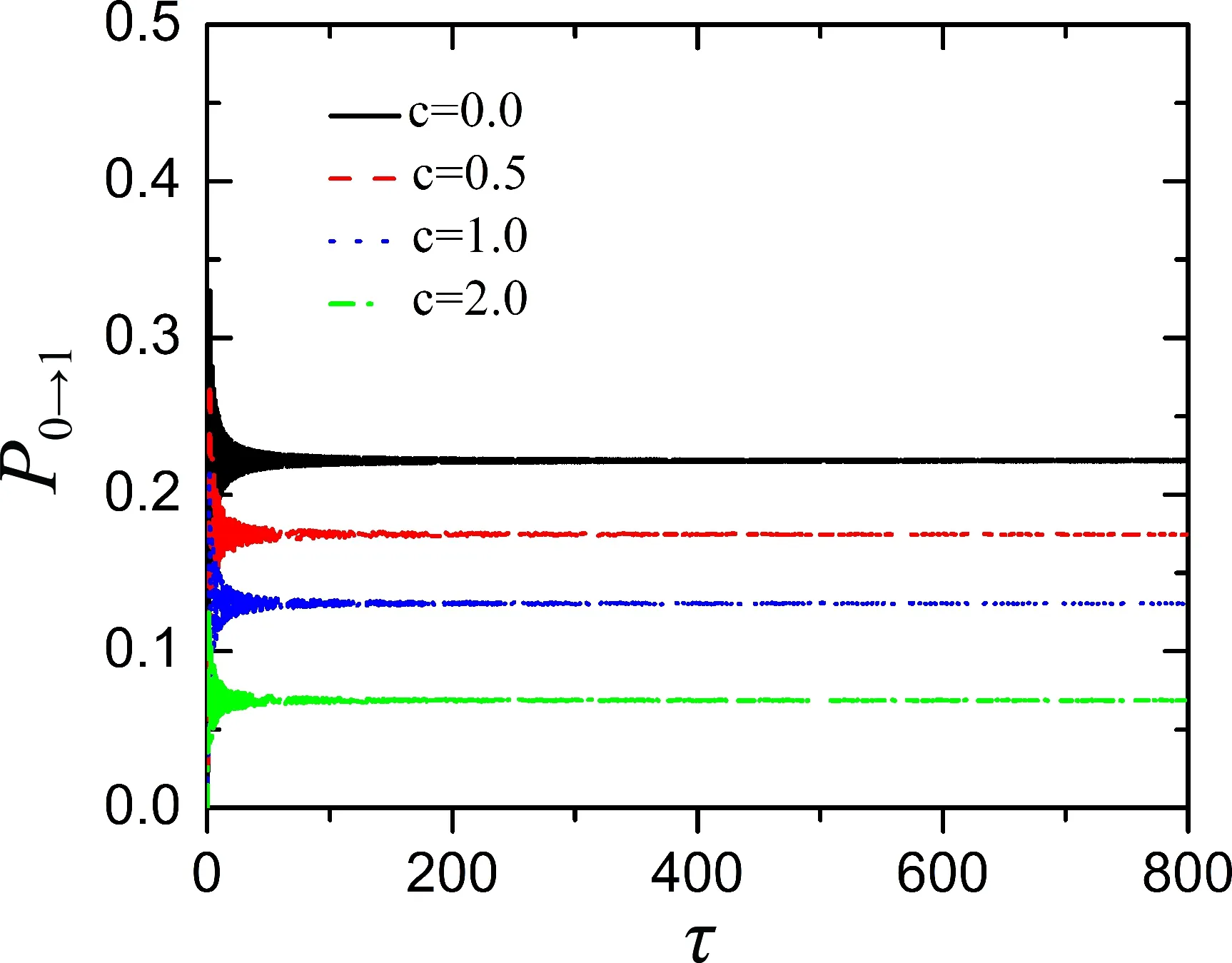
图2 不同非线性强度下跃迁概率随时间τ的变化关系.Fig. 2 The transition probabilities as time τ for different nonlinear strengths.
3.2 能级斜率为负的情形
仍先探究跃迁动力学的一些基本规律. 数值结果如图5-7所示, 图5展示了不同非线性强度下跃迁概率随演化时间的变化关系, 图中取k2=0.2,β=-1.0,g=0.3. 根据(10)式可得到相互作用的临界值c=2.09964, 弱非线性和强非线性就分别对应于c<2.09964和c>2.09964. 可以看出随着时间的增大, 不论相互作用的强弱, 最后跃迁概率都会到达一个稳定值. 对于弱非线性情形, 随着非线性强度的增大跃迁概率会增加, 相互作用促进了跃迁的发生. 而对于强非线性, 跃迁动力学变得复杂. 图6展示了不同非线性强度下跃迁概率随耦合强度、能级斜率以及能级曲率平方的变化. 其中棕色方块线表示c=0.0的解析结果. 为进一步揭示粒子间相互作用对跃迁动力学的影响, 计算了跃迁概率随非线性强度的变化, 如图7所示. 我们发现弱非线性确实会促进能级间的非绝热跃迁, 而在强非线性时, 由于能级拓扑结构发生变化, 跃迁概率会出现振荡, 且随着非线性强度的增大, 振荡幅度逐渐减小, 整体而言粒子间强相互作用会抑制能级间的非绝热跃迁.
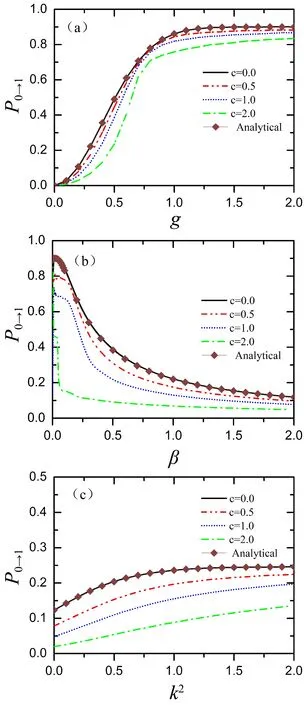
图3 (a)k2=0.7,β=1.0时不同非线性强度下跃迁概率随耦合强度g的变化关系; (b)k2=0.7, g=0.3时不同非线性强度下跃迁概率随|1〉态的能级斜率β的变化关系; (c)β=1.0, g=0.3时不同非线性强度下跃迁概率随|0〉态的能级曲率的平方k2的变化关系.Fig. 3 (a)The transition probabilities as coupling strength g for different nonlinear strengths with k2=0.7,β=1.0; (b)The transition probabilities as the slope of energy level of the |1〉 state β for different nonlinear strengths with k2=0.7,g=0.3; (c)The transition probabilities as the square of the curvature of energy level of the |0〉state k2 for different nonlinear strengths with β=1.0,g=0.3.

图4 跃迁概率随非线性强度c的变化关系. 参数分别取k2=0.7,β=1.0,g=0.3.Fig. 4 The transition probabilities as nonlinear strength c with k2=0.7,β=1.0,g=0.3.
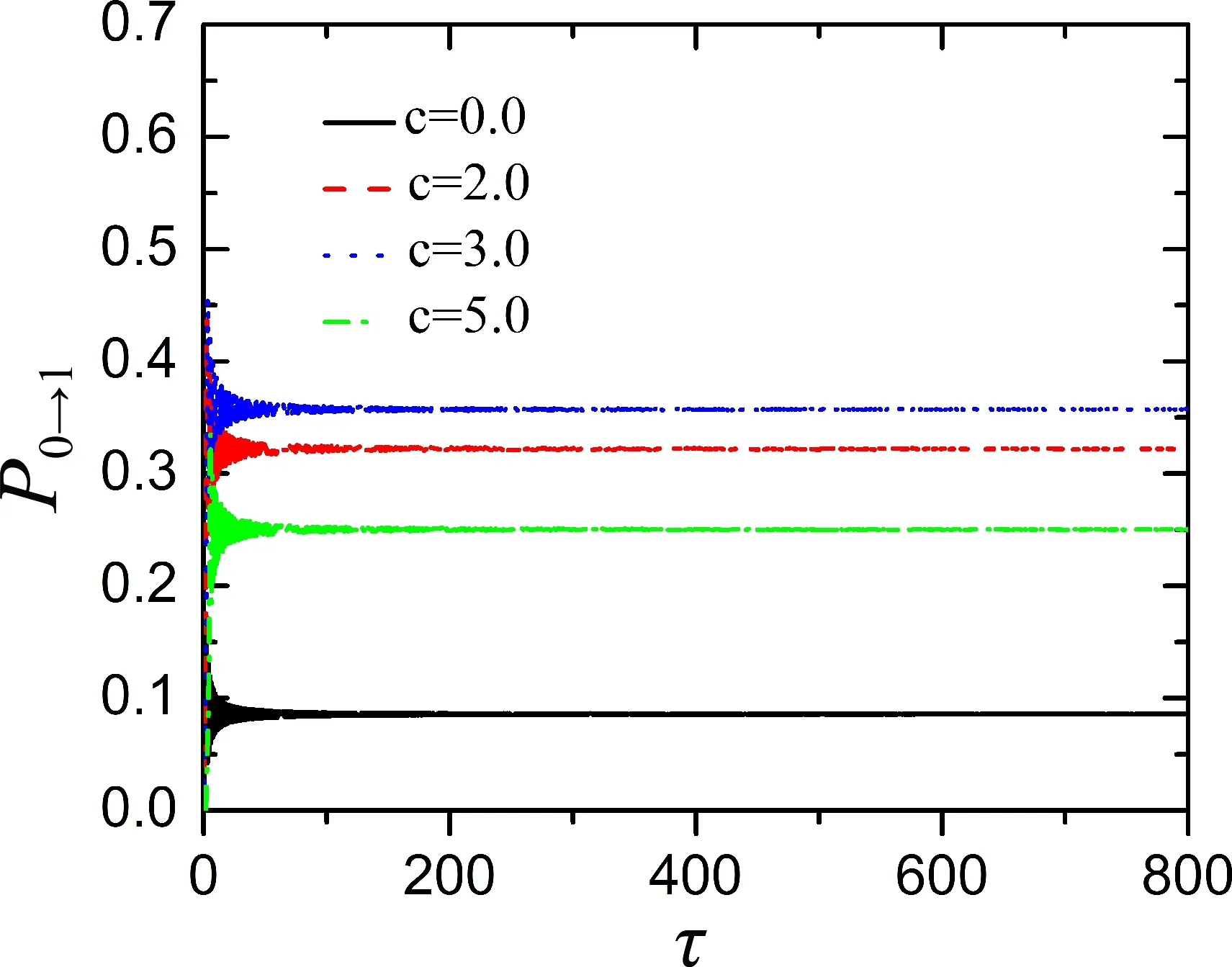
图5 不同非线性强度下跃迁概率随时间τ的变化关系.Fig. 5 The transition probabilities as time τ for different nonlinear strengths.
4 结 论
研究了具有粒子间相互作用的两能级系统Landau-Zener-Coulomb跃迁动力学. 研究结果表明, 在能级斜率为正和为负两种情况下, 粒子间相互作用对能级间的非绝热跃迁会产生完全不同的影响. 为正时, 粒子间相互作用会抑制能级间的非绝热跃迁, 且相互作用强度越大, 两能级间的非绝热跃迁也就越难发生. 而为负时, 弱相互作用会促进能级间的非绝热跃迁, 在强相互作用时, 跃迁概率会出现振荡, 随着相互作用强度的增大, 振荡幅度逐渐减小, 能级间的非绝热跃迁受到抑制.
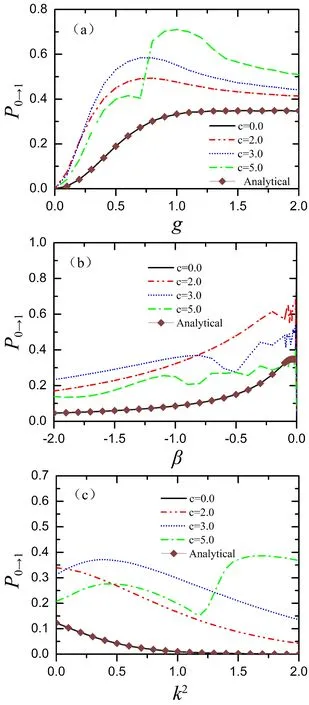
图6 (a)k2=0.2,β=-1.0时不同非线性强度下跃迁概率随耦合强度g的变化关系; (b)k2=0.2,g=0.3时不同非线性强度下跃迁概率随|1〉态的能级斜率β的变化关系; (c)β=-1.0,g=0.3时不同非线性强度下跃迁概率随|0〉态的能级曲率的平方k2的变化关系.Fig. 6 (a)The transition probabilities as coupling strength g for different nonlinear strengths with k2=0.2,β=-1.0; (b)The transition probabilities as the slope of energy level of the |1〉state β for different nonlinear strengths with k2=0.2,g=0.3; (c)The transition probabilities as the square of the curvature of energy level of the |0〉state k2 for different nonlinear strengths with β=-1.0,g=0.3.
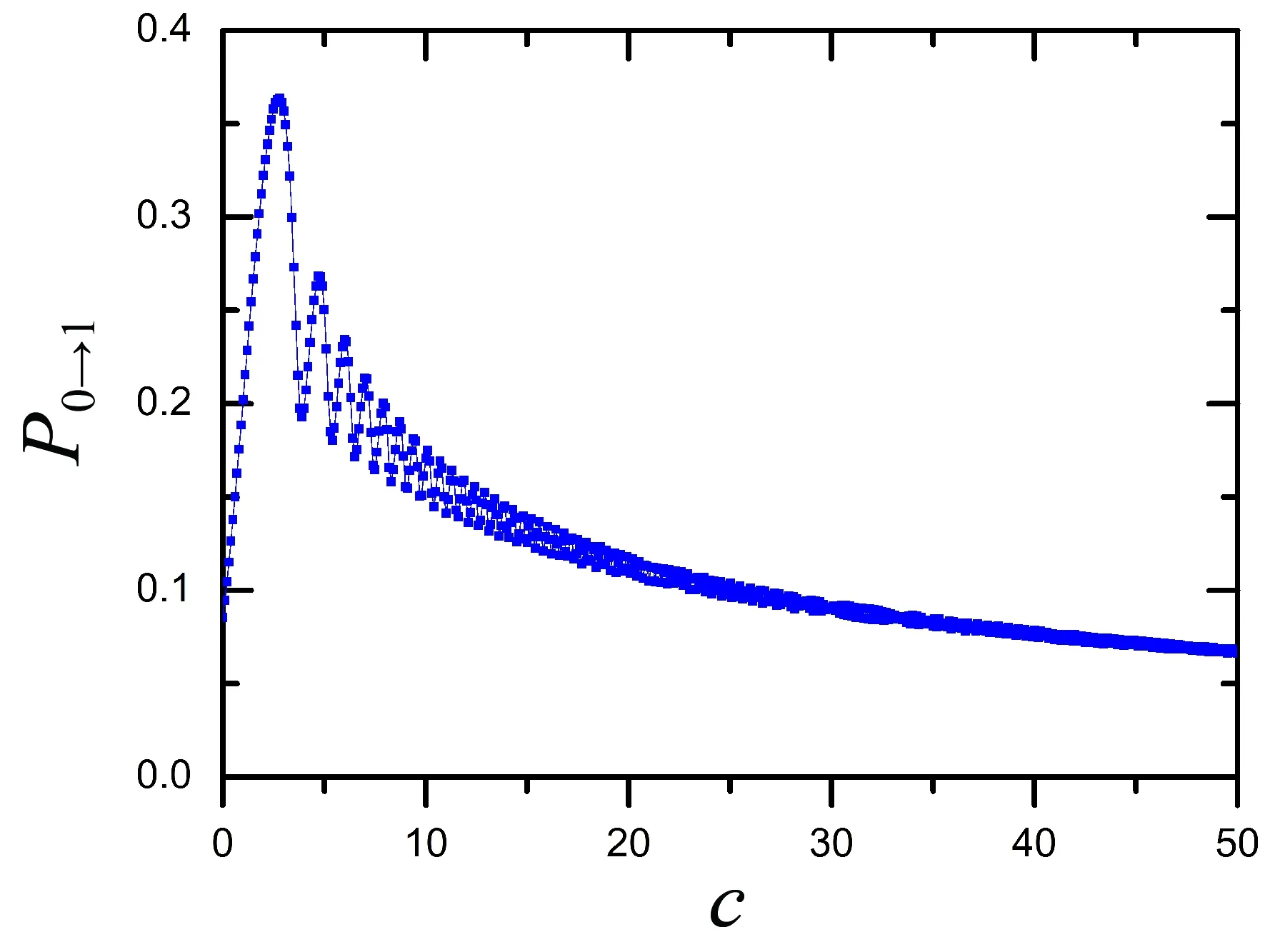
图7 跃迁概率随非线性强度c的变化关系. 参数分别取k2=0.2, β=-1.0, g=0.3.Fig. 7 The transition probabilities as nonlinear strength c with k2=0.2, β=-1.0, g=0.3.

