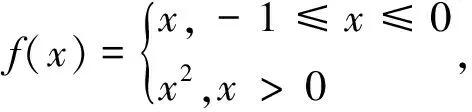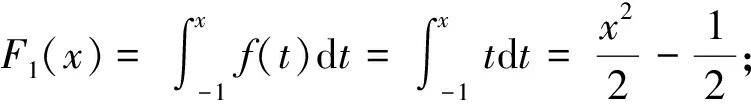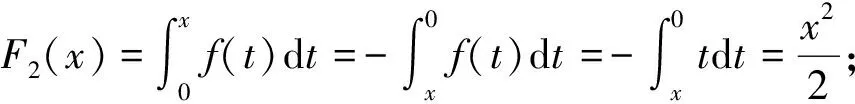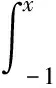关于定积分基本概念与性质的常见题型和解题思路

赵莉莉

(云南大学 数学与统计学院，云南 昆明 650091)

0 引言

定积分的定义能够将微分与积分这一对立的概念有机地统一起来，不仅具有理论意义，还有很大的应用价值，能够解决大量的实际问题，在历年的考研试题中，一直是考核的重点与难点。本文汇总了关于定积分的基本概念与性质的常见题型，并给出了相应的解题思路分析。

1 利用定积分的定义计算数列的极限

定积分的本质是和式的极限[1-2]，而且与区间的划分法以及点的取法没有关系，因此，可以利用定积分计算数列的极限。

例1求数列极限

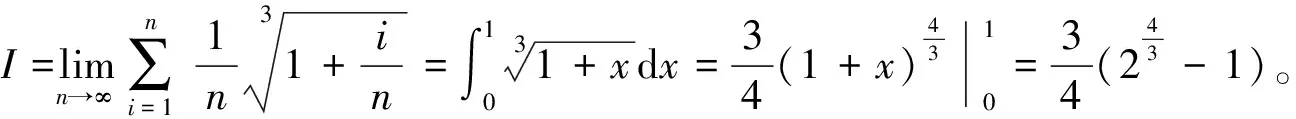
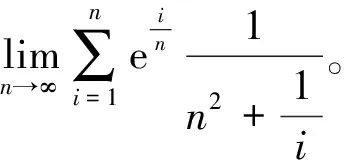
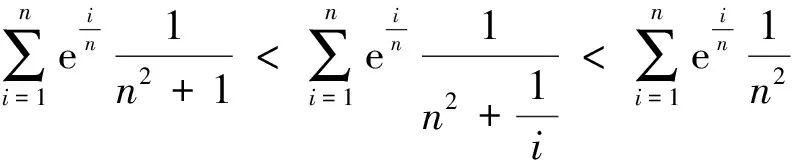
注：所求的数列极限，不一定刚好是某一个和式的极限，可以通过定积分的方式得到答案，但有时可以适当放缩数列的通项，利用夹击定理，求出结果。

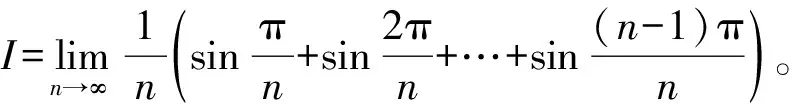
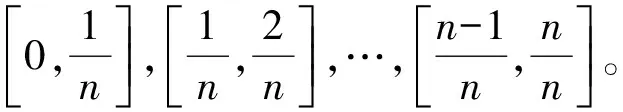
注：定积分的值与区间的划分法，以及点的取法没有关系，在用定积分的定义求数列极限时，一般取的是特殊的点：左端点、右端点或者是小区间的中点。

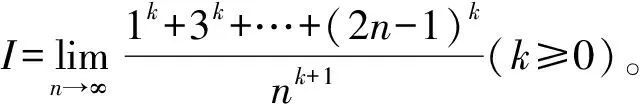
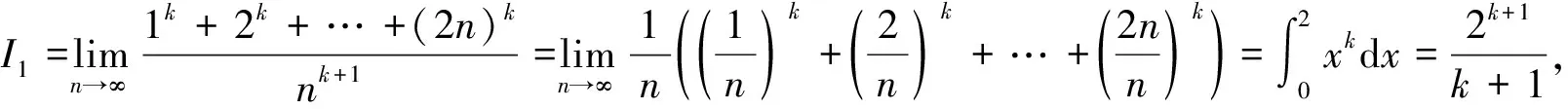
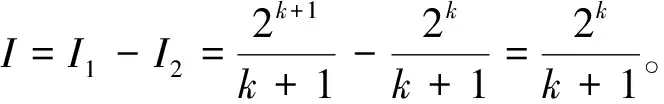
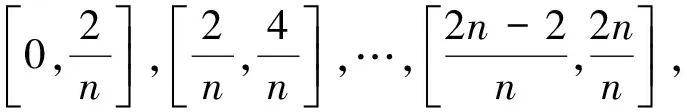
2 定积分性质的应用

2.1 比较定积分的大小

一般来说，可以利用定积分的单调性或者保号性判断两个定积分的大小。

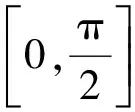
2.2 估算定积分的值

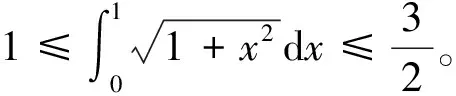
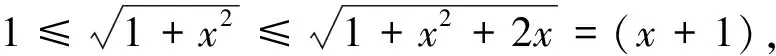
2.3 证明不等式

遇到两个函数乘积或两个定积分乘积，相关的积分不等式的证明，通常需要用到Cauchy-Schwarz不等式[3-6]。设f(x),g(x)均在区间[a,b]上可积，则

例7设f(x)是闭区间[0,1]上的连续函数，且f(x)≥x(∀x∈[0,1])，则

证明

例8设a>0,f′(x)在闭区间[0,a]上，恒大于零且连续，以及f(0)<0，证明

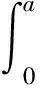
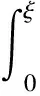
注：积分中值定理是联结函数、函数值，以及积分上、下限的一个桥梁，因此，如果不等式中出现了函数值、函数在某一个闭区间上的定积分，以及函数的导数，可以考虑利用积分中值定理以及微积分基本公式进行证明。

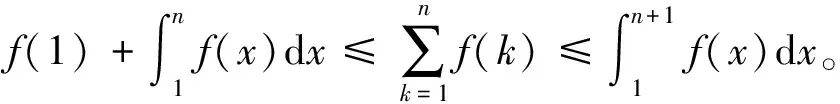
证明

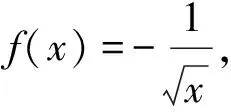
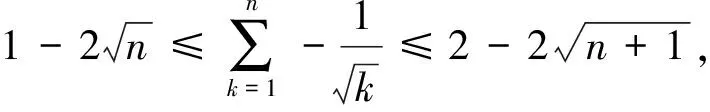
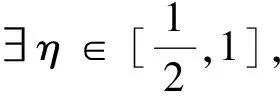
注：因为积分中值定理与被积函数在闭区间上的平均值有关，所以，若题目中出现了定积分等于被积函数在积分区间以外的某点的函数值，要证明区间中某点处的一阶导数为零，不妨使用积分中值定理，并结合罗尔中值定理证明。

2.4 利用定积分的性质求数列的极限

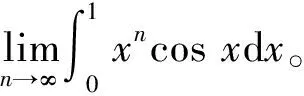
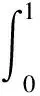
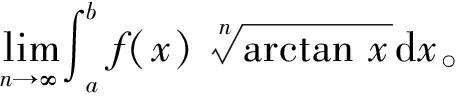
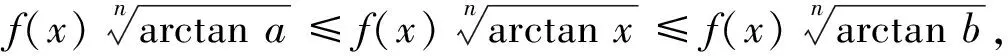
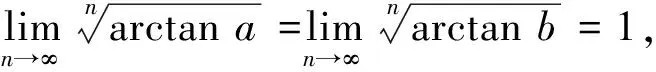
注：若定积分的被积函数中含有有界函数，或者被积函数中的某部分函数具有单调性，一般可以利用定积分的单调性加上夹击准则，求定积分的极限。

2.5 由积分等式，求未知函数

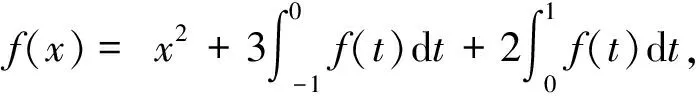
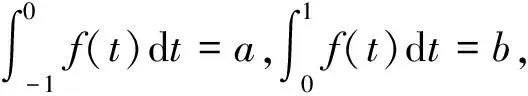
注：1)由积分等式求未知函数时，需要牢记定积分仅是一个与被积函数、积分区间有关的常数，其与积分变量无关。

即F(x)在x=1处不可导，与原函数的定义矛盾。所以f(x)在[0,2]上不具有原函数。

3 求变限积分函数的表达式

给出分段函数的表达式，求以分段函数作为被积函数的变限积分函数的表达式，关键在于对变限积分函数的极限进行分类。