基于突发因素下银行最优信贷策略研究

丁 青，赵雨姗，王 雨，王少珍

(湖南财政经济学院 数学与统计学院，湖南 长沙 410205)

0 引言

近年来，针对企业贷款决策的问题已有很多学者进行了研究分析与讨论。

朱惠琳[1]分析如何减少市场经济风险以及促进银行信贷业务优化。叶莉等[2]针对中小企业贷款利率定价探究中小银行与国有银行竞争策略的演化轨迹及内外部影响因素。李钰博等[3]通过熵权法的应用,构建中小微企业的综合得分模型,确定是否给予中小微企业贷款，并且在年度信贷总额固定时,对这些企业是否放贷,贷款额度及贷款利率方面的信贷策略。刘亚[4]分析了小微企业财务报表在银行信贷决策中的困境，并试图找到独立、客观、高效的第三方信息，在企业财务信息和经营信息之间架起一座稳固的桥梁，为信贷正确决策提供依据。朱皓[5]以小微企业的信贷风险作为研究目标，找出小微企业在信贷业务风险管理的问题。张伟如[6]从经济学的角度分析了商业银行对小微企业“惜贷”的原因。

这些研究的主要方向均从如何制定一个合理的中小微企业的信贷决策出发，都根据现状发表了自己的见解。由于中小微企业在我国的经济发展中占有重要地位，其融资难、融资贵等问题需要得到有力的解决。

在前人研究的基础上，笔者对 123 家有信贷记录的企业的信贷风险进行量化分析，通过建立数据模型，可以高效地发现企业在突发因素的影响下对其贷款信誉的影响，有利于银行对企业的贷款策略作出调整。

1 建立正常情况下的银行最优信贷策略模型

1.1 数据预处理，建立层次结构模型

结合银行对于信誉等级为D的企业原则上不予放贷的规定以及违约企业无论信誉等级高低都不予放贷的假定条件，对123家有信贷记录的企业在正常情况下的信誉评级、发票信息等运营数据及经营数据进行分析与预处理。

根据企业的信用等级、运营时长、企业规模、企业的资金波动、企业间的联系(供求关系)、利率与客户流失率等11个指标，从企业信用、企业实力和未来发展稳定性3个维度，以信誉等级(C1)、总体价税合计(C2)、企业各月价税合计标准差(C3)作为关键指标，采用层次分析法建立企业信贷风险评价体系(图1)。

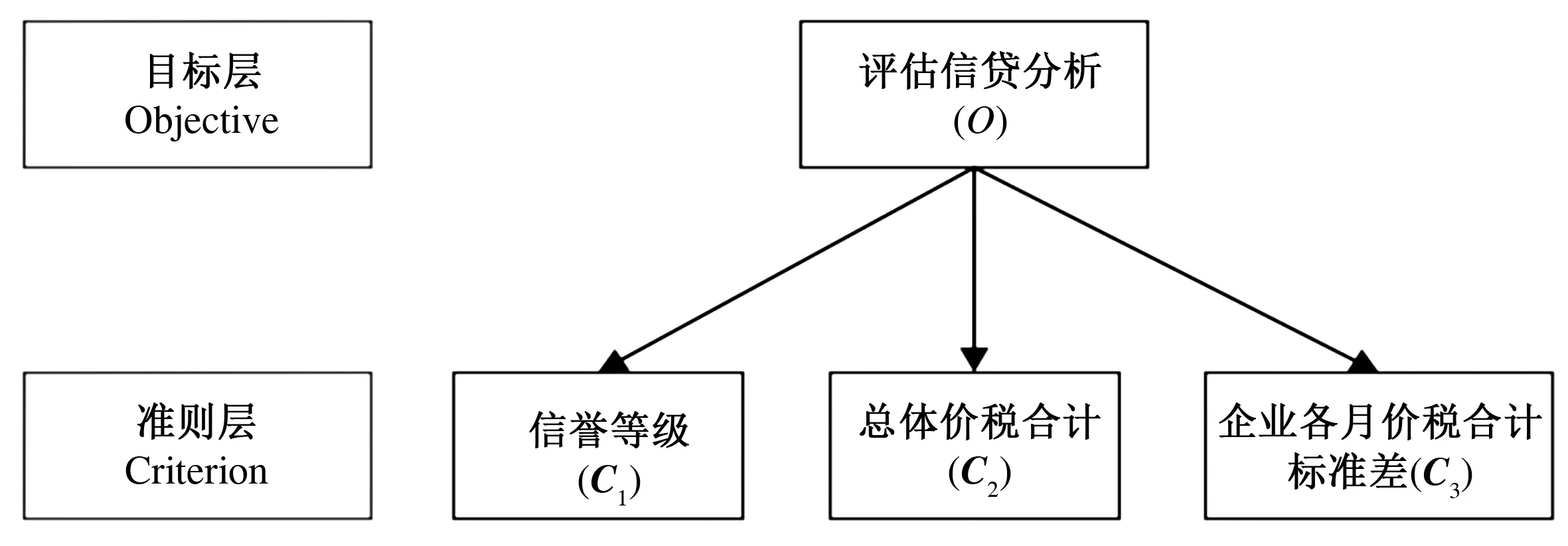
图1 对决策问题建立的递阶层次结构模型

1.2 建立加权评价模型

1.2.1 构造判断矩阵

构造O-C判断矩阵C1-P，C2-P，C3-P，如表1所示。

表1 O-C判断矩阵

1.2.2 对判断矩阵进行一致性检验

首先，求出O-C判断矩阵的特征值λmax= 3.009 2，由公式

(1)

计算出一致性指标CI=0.004 6，平均随机一致性指标RI与n的关系如表2所示。

表2 n与RI的关系

再根据

(2)

计算出CR=0.008 8<0.1，故O-C判断矩阵通过一致性检验。

1.2.3 分别用算术平均法、几何平均法、特征值法计算权重

假设判断矩阵

通过算术平均法求得权重向量分量

(3)

通过几何平均法求得权重向量分量

(4)

将算术平均法、几何平均法、特征值法得到的权重进行平均，再通过特征值法，求出矩阵JM的最大特征值以及其对应的特征向量，将求出的特征向量进行归一化即可得到最终的权重向量，如表3所示。

表3 由算术平均法、几何平均法、特征值法得到的权重向量

使用倒数法将极小型指标(企业各月价税合计标准差越小越好，这样的数据称为极小型指标)转为极大型指标(信誉等级、净利润数据越高越好，这样的数据称为极大型指标)，以达到指标同趋势化的效果，得到正向化数据。

随后，对已正向化数据进行标准化处理以消除不同指标量纲的影响，

(5)

采用特征值法确定指标权重，基于TOPSIS(technique for order preference by similarity to ideal solution)方法加权得到最后的量化值，以量化各企业的信贷风险，得到企业信贷风险量化体系，对企业的信贷风险进行评级，与原有的企业信誉等级对比，验证模型的可行性。

将量化值与信誉等级进行比对，结果为95.78%，由于对比正确率超过95%的数据成立，所以模型成立。

1.3 建立正常情况下的银行最优信贷策略模型

依据违约金字塔理论[7]，银行要实现盈利性与安全性的统一，就需要使得贷款利率与信誉等级相关，保证信贷风险越低。信誉等级越高的企业融资越快，取得的贷款额度和贷款利率也越低。相应地，当信誉等级越低，取得的贷款额度和贷款利率就会越高，即利用利润最大化和风险最小化的经营原则构建银行最优信贷策略模型，用来判断银行是否选择对企业放贷，并给出最佳贷款利率和最佳贷款额度。

同时，银行对于信誉等级为D的企业原则上不予放贷的规定以及违约企业无论信誉等级高低都不予放贷的假定条件仍然成立。所以，

再根据公式结合企业数据与前期设定的量化标准，可以计算出企业在一定范围内能够获得的贷款金额(此时达到银行能够给出的最佳贷款额度)，

(6)

同样地，贷款年利率与客户流失量存在一定关系，所以设银行每年对企业的贷款收益W，每年给单个企业贷款的金额m，给单个企业总贷款为M，年利率为ρ，客户流失量为μ。运用公式(7)，计算出每一家企业取得贷款时的贷款利率值，

(7)

总的来说，

2 对突发事件和企业的分类

针对突发事件和企业性质，确定合适的分类标准。一般来说，突发事件根据性质可以分为自然灾害、事故灾难、公共卫生事件、社会安全事件四类；企业可以分为服务业、制造业、高新技术产业、个体经营等类型。为简化对突发事件影响分析的复杂程度，基于上述准则对突发事件及企业进行分类。

3 引入影响因子，识别突发因素对企业的影响

考虑到不同突发事件对不同行业的具体影响和影响程度不同，为分析突发事件对企业的真正影响，我们需要对其进行比较。对此设定一个影响因子，基于影响因子越强，影响力越大的理论，衡量突发事件对企业影响程度的大小，进而判断银行对企业进行放贷的考虑程度(表4)。

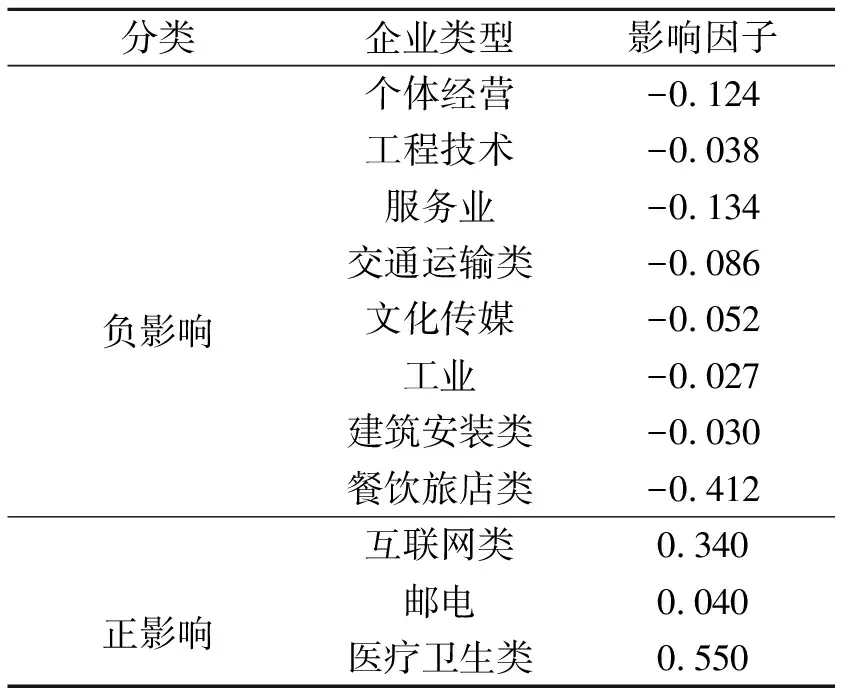
表4 影响因子

4 改进原有策略模型，得到基于突发因素下银行最优信贷策略方案

在原来模型的基础上考虑突发因素的影响程度，通过向企业信贷风险量化体系中加入影响因子，对原来的模型进行改进和调整，更准确地量化中小微企业基于突发事件的信贷风险，基于突发事件的最优信贷决策模型，运用公式

量化值(影响后)=(影响因子+1)×量化值(影响前)

(8)

求解发生突发事件时的信贷调整策略。例如，假设某种传染病暴发对企业有重大影响，对产生负影响的企业，银行对其放贷策略可以在一定范围内进行缩小或选择不对企业进一步放贷；对产生正影响的企业，银行对其放贷策略可以在一定范围内选择增大；而对产生间接影响，甚至是无影响的企业，银行对其放贷策略可以选择保持不变或小范围内进行最优化调整。据此，最终获得基于突发事件下银行最优信贷策略方案。

5 模型创新点和特色

1)使用熵权法对各项指标进行赋权后，使用TOPSIS方法量化各企业的信贷风险，使企业信贷风险体系更具体化；

2)对突发事件及企业的分类依据分类准则进行分类，在一定程度上简化对突发事件影响分析的复杂程度，节省了较多花费在不同突发事件、相同突发因素影响下对企业的影响识别时间；

3)引入影响因子，着手实现突发因素带来风险的量化，能够较好地转化为银行放贷决策的重要参考指标之一；

4)将影响因子与已有数据进行整合得到的结果代入正常情况下银行的最优信贷策略模型，与原有方案进行任务成功率的对比，保证改进后的模型能够在实际情况下使用；

5)运用较多的数学模型以及数学分析方法，考虑了多个突发因素对企业及银行作出信贷决策的影响，使得模型更好地接近实际，实现灵活性、安全性和有效性的统一，一定程度降低突发因素对银行信贷风险的影响。

6 结论与建议

本文基于银行对于信誉等级为D的企业原则上不予放贷的规定以及违约企业无论信誉等级高低都不予放贷的假定条件，通过数学建模建立企业信贷风险评价体系，研究企业在融资过程中受到突发因素影响时，针对不同突发因素对不同行业、不同类别企业的不同影响，给出银行最优贷款决策。

首先，基于已有信誉等级的企业数据建立企业信贷风险评价体系，使用熵权法和TOPSIS方法量化信贷风险，依据RAROC(risk-adjusted return on capital)理论[9]、违约金字塔理论及利润最大化和风险最小化的经营原则，构建正常情况下的银行最优信贷策略模型；其次，对突发事件和企业进行分类，引入影响因子，识别并量化突发事件对企业的风向影响，将得到的量化值结果代入正常情况下银行的最优信贷策略模型，采用Logistics函数对模型进行检验，与原有方案进行任务成功率的对比；最后，在原来模型的基础上综合影响因子，改进和调整模型，求解发生突发事件时的最优信贷调整策略，得到风险情况下的银行最优信贷策略模型。

基于本研究，银行可根据不同行业的企业进行信誉等级的划分和确定，明确指出不给予信誉程度低的中小微企业贷款支持，对正常信誉程度下的企业建立最优信贷策略模型，在响应国家政策的条件下，最大限度降低银行资本损失率；当企业出现突发事件而影响企业经营时，银行应该要将预测的风险影响量化并代入决策模型中进行检验，观察结果的好坏，并根据结果对原有贷款方案进行修改，使决策方案符合信贷主体双方对利益的预期，降低双方的风险，从而形成最优信贷决策方案。

模型主要解决以下3个方面的问题。

1)对正常情况下银行对企业的最优信贷策略进行分析，建立银行最优信贷策略模型，判断银行在何种情况下选择对企业放贷，并给出最佳贷款利率和最佳贷款额度；

2)针对突发事件和企业性质，作出合适的分类标准，并引入影响因子概念，考虑如何识别突发事件对企业的影响；

3)对不同的中小微企业抗风险能力的不同，考虑不同突发事件对中小微企业影响程度不同，银行应如何利用量化后的影响因子改进原有模型，并在其基础上如何使用改进模型制定最优信贷调整策略。

此外，该模型还可以推广至其他的决策研究，如股票投资决策等。但是，考虑到技术方面的不足、突发因素的多样性及突发因素对企业影响的不可测，目前难以建立一个较为完善的基于突发因素下的银行最优信贷策略模型，对其信贷决策也无法完全达到最优的状态。