基于特征值反问题下的图像修复

程 鹏，陈 伟

(华北水利水电大学 数学与统计学院, 河南 郑州 450046)

0 引言

图像分割与修复是图像识别的关键步骤，图像修复技术的应用已经遍布各个领域。随着图像修复应用技术的适用范围越来越广，人们对图像修复效果及质量的要求也在不断提高。而在图像技术不断发展的今天，图像修复技术仍有很多问题是传统修复算法难以处理和解决的。因此学者不断探索将新兴理论与图像修复相结合的方法。本文探究特征值反问题下的图像修复，首先介绍关于实对称带状矩阵相关的研究。

给定

r>0是一个整数，|i-j|>r时aij=0，i=1,2,…,n;j=1,2,…,n。在(i,i+r)元素所在的对角上至少有一个元素非零，则称A(r)为带宽为2r+1的实对称带状矩阵。

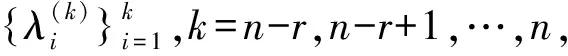
(1)

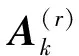
1984年BOLEY D L等[1]对问题1给出了r=2时、n为偶数、公式(1)仅为严格不等式的情形，采用块Lanczos方法，给出问题1的解。随后BOLEY D L 等[2]在r能整除n的情况下给出了问题1的解。FRIEDLAND S[3]对r=n-1给出问题1的一个解。1989年，殷庆祥[4]给出了拟Lanczos方法，取消了r能整除n的限制。1987年，戴华[5-7]采用广义块Lanczos方法，不仅取消了r能整除n的限制，且不必所有特征值满足公式(1)严格不等式的情形。其中戴华的方法灵活性更强且受限制更小，能解决问题的范围更加广泛。随后诸多学者对于此类相关的特征值反问题进行了不同的研究[8-25]。

本文建立在图像数据的基础上进行探索，也就是说，本文所研究的实对称带状矩阵假设一定存在，且实对称带状矩阵的各元素满足取值范围为1～255。为此提出问题2、问题3两个关于图像修复的新问题。

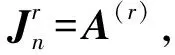
1 预备知识

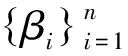
βi≤αi≤βi+1,i=1,2,…,n-1,

R(λ)=(T(λ),S(λ))表示T(λ)和S(λ)的首项系数是1的最大公因式，

其中

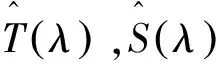
νi≤μi≤νi+1,i=1,2,…,k-1，

(2)

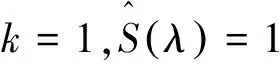
I(z)={j|αj=z,j=1,2,…,n-1}，

则(bn1,bn2,…,bnn)为矩阵B的最后一行的充分必要条件是bni(i=1,2,…,n)满足方程组

(3)

方程组(3)有有限个解的充分必要条件是：当αi(i=1,2,…,n)是S(λ)的m>1重零点时，αi是T(λ)的至少m重零点，这时方程组(3)恰有2k-1个不同的解。

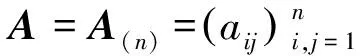
2 问题2的求解

由引理1和引理2可知实对称带状矩阵加边构造的过程，但在加边构造过程中难以保持矩阵带宽不变。本文是建立在实对称带状矩阵已经存在的基础上进行研究的，为此需要维持所加的边使矩阵始终保持带状形式，并且这样的构造是唯一的。

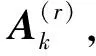
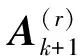
令

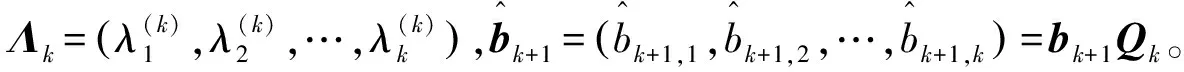
(4)

的解。

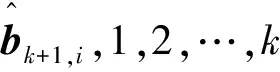
(5)

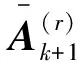
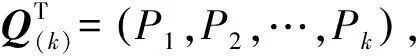
tPi=0,i=1,2,…,k-r

(6)

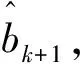
定理1由上述方法构造的实对称带状矩阵A(r)是唯一的。

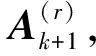
dk+1≠bk+1,

(7)

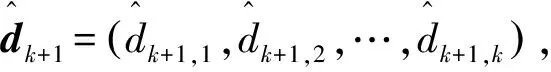
(8)

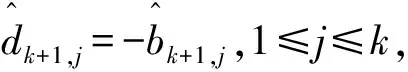
G1=f1G2+…+fk-1Gk,

(9)

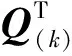
(10)

将公式(10)带入公式(9)可以推出公式(9)不成立,所以dk+1=bk+1，构造的实对称带状矩阵A(r)是唯一的。

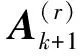
3 问题3的求解

给出Jacobi 矩阵

这里ai,bi∈R，且bi>0，Ji是Jn的顺序主子矩阵,i=1,2,…,n。

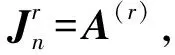
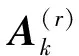
证明略(当然可以检验它的正确性)。

令

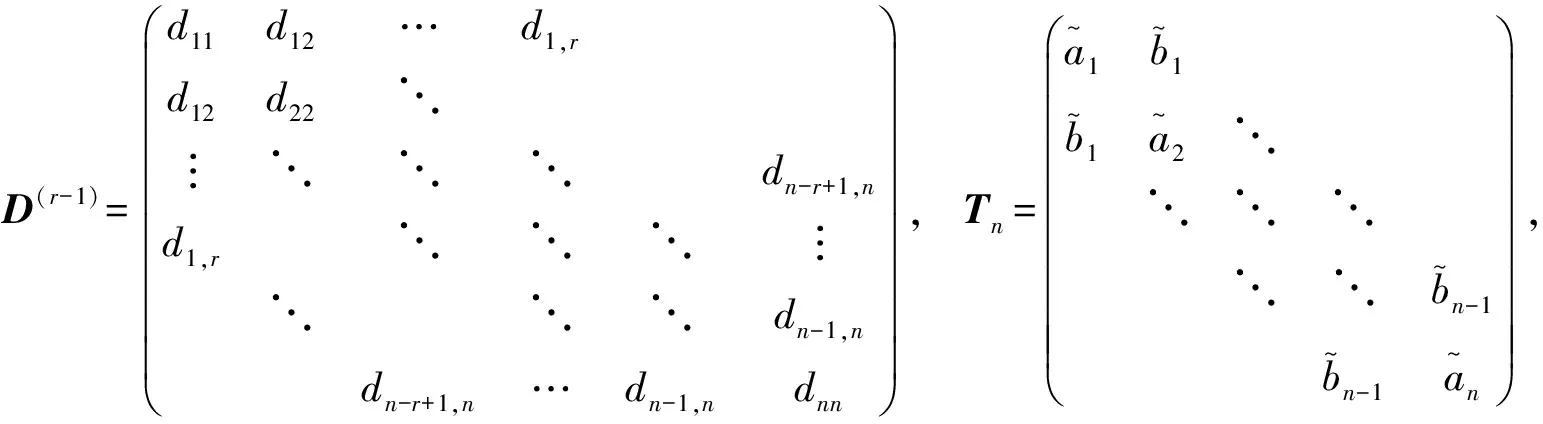
D(r-1)和Tn中所有的元素未知。满足

D(r-1)·Tn=A(r)。

(11)

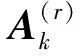
故由公式(11)知

(12)

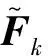
(2k-r-1)r+k≥r(r+1)/2+(k-r)r+r-1+2k,

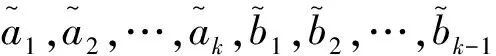
由引理3知，当

(13)

则Tk=Jk。

4 算法步骤

4.1 问题2的算法

4.2 问题3的算法

1)通过公式(11)确定建立方程组；

2)由公式(12)和公式(13)求出Jk；

3)由文献[18]或[13]结合已知条件构造Jn；

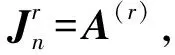
5 图像的修复

本文通过特征值反问题处理图像，要保证图像的对称性，对于普通图像可以通过中心对称得到一个对称图像，下面对两类问题进行不同的分析。

5.1 问题2下的图像修复

图1是原始黑白图像。这是一个对称图像，通过MATLAB软件对其逆时针旋转45°得到图2，提取图2数据，可以发现图2是在方阵中，白色位置分元素值为255，为体现本文的研究需要，对其空白部分数据进行适当改变。

图1 原图

图2 旋转后图像

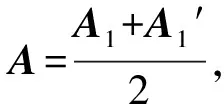
矩阵A转换成的图像就是图3，此时矩阵A满足实对称带状矩阵的条件，对图3所生成的矩阵A各阶顺序主子矩阵的特征值进行提取，使其满足问题1的条件，图4是损坏的图像，可用问题2的解法修复图4。

图3 填充后的图像

图4 损坏的图像

图5是修复后的图像，图6是对图5图像的截取，也是修复后的图像，对比图1可以发现图像是相同的，数据分析得到问题1的解法在图像数据的还原上基本误差在1范围内，所呈现的图像效果也是良好的。

图5 修复后的图像

图6 图像的截取

从问题2的解法可以看出，只能修复图像的3/4，如果是另外1/4受损时，可以在保留数据时对图像所生成的矩阵旋转180°，保留旋转后所生成矩阵的各阶顺序主子矩阵的特征值。

5.2 问题3下的图像修复

图7是随机生成矩阵所呈现的图像，图8是去除矩阵一部分数据后得到的图像，图9是修复后的图像。可见白色区域数值十分庞大，数据的变换从图像中很难看出差距，白色区域的数值在构造矩阵过程中数值十分不稳定,数值往往会改变很大，但在图像上依旧呈现白色。但如果是普通图像满足问题3的条件，那么它的值在计算过程中改变是十分小的，对于成像过程基本上不会出现太大差距。如果能够改变上下三角矩阵的像素大小使其可以一直满足问题3的条件，那这个解法适用性就很广泛了。相关的结论在今后的研究中会继续探讨。

图7 原图

图8 损坏的原图

图9 修复后的图像

5.3 图像的还原

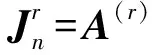
设B=(bij)是任意一个n阶实对称矩阵，取变换H1使

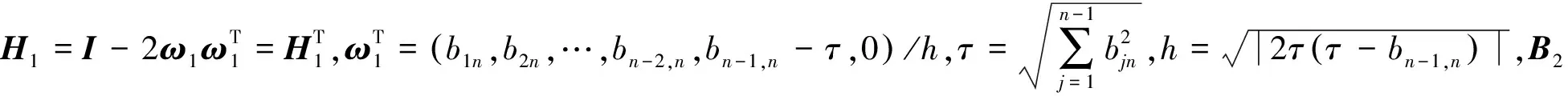
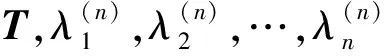
通过此方法还原图1，图10是还原后图像，图11是对图10中图像的截取。

图10 还原后的图像

图11 图像的截取

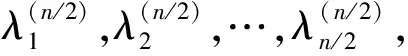
6 总结

从文章可以看出两类特征值反问题对于图像的修复都是可行的，问题2方法的优越性在于其修复的图像与原图像几乎一模一样，它们所生成的矩阵忽略像素值千分位时两者的像素值基本是相同的。问题3的精确性取决于Jacobi构造时的精确性，而相关的Jacobi矩阵构造证明是相当成熟的，所以问题3的方法也是可行的。对于图像的还原是关于图像修复的另类探索，可以看出本文还原的图像效果是很好的。图像的数据在矩阵领域讨论，特征值反问题无疑是最好、最方便的方法，结合高斯云模型的图像分割技术可以完整地研究图像识别技术中最重要的两个部分。