评时钟佯谬的现代解

孟广达，霍瑞云，王润华

(1.郑州大学，河南 郑州 450001；2.河南财政金融学院，河南 郑州 450046)

0 引言

不知从什么时候起，人们使用“狭义相对论”这个术语时，其含义是有差别的。大多数人还是仅限于惯性参照系；有些人，特别是一些造诣较深的学者，把加速参照系也包括在内了。这个差别并不影响对时钟佯谬的讨论，但必须明确交代，不然会带来毫无价值的争议。我们所说的狭义相对论只限于惯性系。本文中如果不作说明，时钟A总是指相对惯性系不含加速阶段的。

1 问题

20世纪60年代，对时钟佯谬的讨论相当热烈，不少人想在狭义相对论范围内把该佯谬解决，这样的探讨也是有益的，可以加深对相对论中诸多概念的理解。但是，导致出现时钟佯谬的根源是时钟B经历了加速阶段。如果不针对根源而只关心它导致的结果，就不可能顺理成章地解决问题，有关这方面的讨论我们已经阐明过看法[1-2]，本文不再涉及。

长期以来，大多数人容易接受的时钟佯谬的解是：在与时钟B相关联的参照系中岀现了引力场。据说这种解是爱因斯坦提出的。初看起来很难理解，这么简单的一句话，既无运算，又无公式，也无结果，怎么能是问题的解答。冷静一想就恍然大悟了：给出(或求出)时钟B的运动状况，找出与此相应的坐标变换，从而得出时钟B参照系中的度规，代入公式问题就解决了[3]。时钟B的运动状态五花八门，每种状态都有与它相应的坐标变换，不同的坐标变换不可能用几个式子表达岀来。所以时钟佯谬的“通解”就只有这么一句话。对它可作解释，无须增添。

如果深信这个“通解”正确，那就没有必要选择时钟B的某种运动状态进行详细的完整运算。这种运算没有什么价值,充其量也不过可以作为一道习题让学生做。极可能就是由于这个原因，爱因斯坦本人没有给出一个实例来。

对时钟佯谬感兴趣的人对此“通解”并不满足。有相当多的人，总想找个实例。出人意料的是，直到今天，一个多世纪过去了，能给出结果的人屈指可数。即使非常著名的学者也只是给出了近似解[4]，近似解价值不大。据我们所知，只有MØLLER C对一个实例作出了完整的解答[3]。

为何找一个实例这么困难？因为遇到的一些问题难以解决：例如什么是匀加速参照系，如何找出加速参照系与惯性系之间的变换关系。加速参照系中的引力场为何会在全区域同时发生突变而无传播过程……现在看来，爱因斯坦之所以没有给出一个实例，除了上面已经提到的可能之外，也很有可能他本人也难找到一个。试想，时钟佯谬关系到相对论的自洽性，受到广泛的关注[4]，难道他不想给出一个尽量圆满的解答？

MΦLLER C给出的解可能是最好的一个实例，但其中也存在问题有待商榷，只是不容易澄清，很难取得共同的看法。利用他的解法，我们推出了时钟佯谬的解中普遍存在的一个离奇结果：时钟A的读数增量在整个过程的某一阶段是负值，把它通俗化就是“返老还童”[2]，如何处理这个离奇结果有待进一步讨论。

2 时钟佯谬的现代解

为了表述方便，下文中把上述的传统的爱因斯坦解简称为“爱氏解”。

所谓时钟佯谬的现代解，按照文献[5]中的介绍，只有一句话:“时钟记录的是自己的世界线长度。”我们不知道这个解是哪位学者在什么地方首先提岀的，也没见到过该解的原始表述。我们对它的了解大都来自文献[5]。我们觉得该文写得非常出色，读后受益匪浅，可以信赖。如果有引用不妥当，甚至有理解错误之处，敬请指正。

对于接触过相对论，但了解并不多却对时钟佯谬很感兴趣的人，见到现代解会觉得太玄了，所以现代解引不起广泛关注；另一方面，不少相对论方面的专家对它推崇备至，甚至有些学者感概道：“相对论时钟是类时世界线上的里程表，假如人们对于这一事实有过更多的关注,那么在所谓时钟佯谬上付出过的很多努力就可以省略掉了。”[5]如果现代解果真是时钟佯谬的最精辟完美的解，那么爱因斯坦应该太遗憾了。完成了狭义相对论，独自一人创立了引力理论，可惜没有能够完满解决质疑狭义相对论自洽性的时钟佯谬。难道他不知道时钟记录的是自己的世界线长度，不知道长度是坐标变换下的不变量，不知道时钟A的世界线长度比时钟B的长吗?在这些方面谁能比他更熟悉？对于几何学，如果他达不到登峰造极炉火纯青的地步，怎么可能创立他的引力埋论。我们认为不论从哪方面讲，在长达数十年的时间内他不会想不到这样的解。那么他为什么没给出这样的解?难道不值得深思吗？与爱因斯坦解相比现代解还是有些逊色，特别是负面影响严重。

下面我们用甲、乙两方对话的形式把这两种解作一比较。

乙：你为何不支持爱氏解而支持现代解？

甲：首先，现代解简单明了，短短一句话就可以表达清楚：时钟记录的是自己的世界线长度。

乙：是的，一句话内行就明白了。但是爱氏解也不需要两句：引力场的影响。用字更少而且容易被较多的人理解。

甲：这一句话怎么能是一个解，它没给出结果。

乙：现代解的那句话也没有给出结果。

甲：结果非常明显，不必交代。只要在时钟A参照系中画出两个时钟的世界线就一目了然了。

乙：爱氏解也是如此。只要在时钟A参照系中算岀结果即可，而且计算简单，甚至不加思考就可以写出结果。

甲：你没有用到引力场的影响。

乙：同样，你没有在时钟B参照系中画图。

甲：不必在时钟B参照系中画图。世界线长度是坐标变换下的不变量，再画图仍然是时钟A的长，何必徒劳。

乙：同样，我也不必在时钟B参照系中计算，代入公式即得结果,何必徒劳。

甲：你能确保所得结果与时钟A参照系中的结果相同？

乙：你能确保在时钟B参照系中画出的两条世界线的长度之差一定与时钟A参照系中的相同？

甲：可以确保。世界线长度是不变量。

乙：同样，我也可以确保。所用公式正确，怎么不能确保！

甲：用公式计算太难，遇到的问题几乎束手无策，以致于直到现在也没能作出几个解。

乙：难道在时钟B参照系中画出世界线就容易吗？我们还没有见到过这样的图。试问：得出时钟B参照系中的度规容易？不知道度规如何画图？从画出的图判断世界线的长短容易？

让我们选用最简单的实例试想一下吧。

T=0时，时钟B从原点出发沿x轴正方向以速度v匀速运动(图1)。t=T时瞬间反向，沿原路返回到原点。对于这个过程，在时钟A参照系中画出的图与文献[5]中的图相似:时钟A的世界线是一条沿时间轴的直线；时钟B的世界线由两条相交的直线构成。两条世界线的起点和终点分别重合(见图1)。在时钟B参照系中两个时钟的世界线是什么样呢？除了一段无限短的时间外，时钟B参照系也是惯性系，在此时空区域内时钟A以速度v匀速运动瞬间反向后沿原路返回到原点。因此，在时钟B参照系中画出的两个时钟的世界线与在时钟A参照系中画出的非常相似(见图2)。差别是：沿时间轴的直线是时钟B的世界线；不相交的两条直线是时钟A的世界线上的两段,这两条直线的端点无限接近,间隙处为时间无限短的非惯性时空区域，此处的世界线我们画不出，所以是空白。

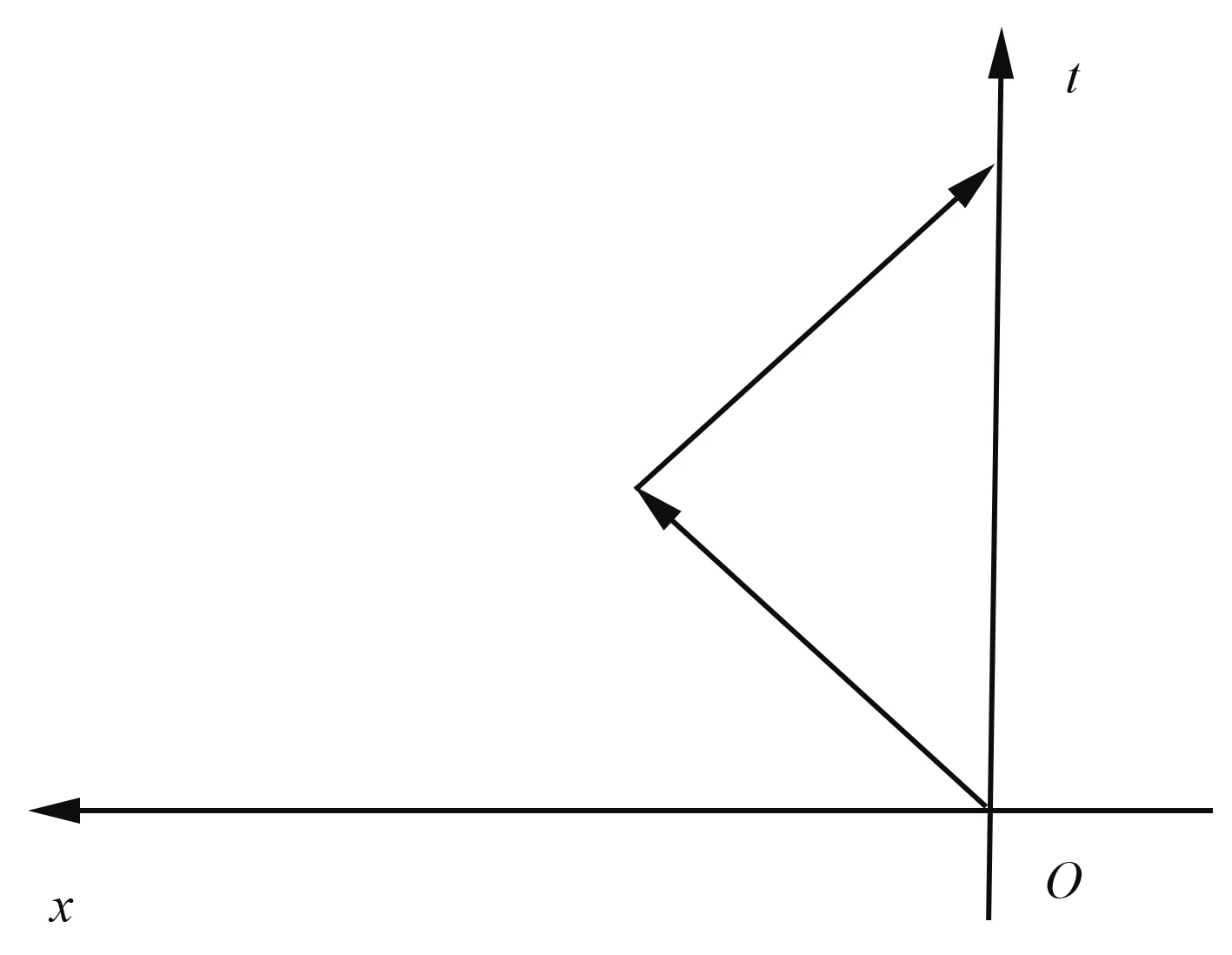
图1 正向

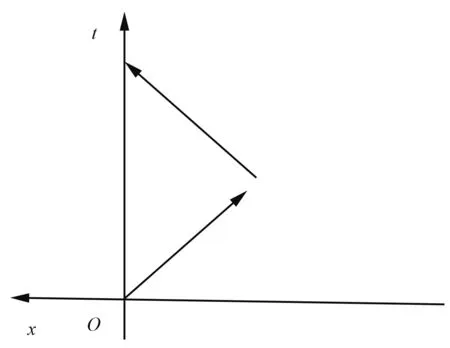
图2 反向

根据所画的世界线可以推出的结论是:在惯性区域内，时钟B的世界线比时钟A的长,因此，如果能得到时钟A的世界线的总长度比时钟B的长。那么在无限小的非惯性时空区域内，时钟A的这一段世界线必需比时钟B的长，而且二者之比为无限大。试问有可能画出时钟A的这一段世界线吗？你能补上吗？

甲：不必画，想象即可。因为世界线的总长度是不变量，所以在这个无限小的时空区域内，时钟A的一定比时钟B的长。

乙：你的回答不合逻辑。讨论实例的目的就是要用实例证实从图上的确可以得出两个时钟的世界线长度都是不变的。怎么能用需要证明的对象作为论证的依据。其实，不是不必画，可能是你根本无法画出来，就是凭想象我们也想象不出。

这样看来，爱氏解就胜过你所支持的现代解。爱氏解不仅可以算出这段世界线的长度，而且可以给岀这个令人惊奇的结果的根源——引力场的影响[3]。

人们对传统的爱氏解不满足，所以总想用实例证实。同样，人们对你称赞的现代解也是不会满足的，必需用实例证实。如果一个实例没有，怎能令人置信。上述实例是极限下的情况，要求在无限小的时空区域画图可能强人所难了，改换成一个加速区域为有限大小的过程吧。我们建议采用文献[3]讨论时钟佯谬时选用的那个实例。如果把文献[2]中涉及时钟读数增量为负值的过程也包含进去就更好了，显示一下几何图中如何表示时钟读数的负增量。

从以上的对话可见，现代解绝对不可能是时钟佯谬的最精辟完美的最终解。它与爱氏解各有所长，相比之下还是不如爱氏解。对于具体的实例爱氏解的确遇到了很大困难，以至直到现在，据我们所知，所有已经讨论过的实例没有一个不存在需要商榷、有待进一步讨论的地方。在相当长的时间内人们热衷于在狭义相对论范围内解决时钟佯谬。之所以如此，一个主要的原因就是爱氏解遇到的困难太大，几乎束手无策。事实上遇到困难并不是坏事而是好事，对于深入理解相对论十分有益。现代解用几何语言回避困难，看似十分巧妙、精彩地解决了问题，事实上不仅没有把问题解决，而且还有很不好的影响。试问，遇到困难不认真思考产生困难的原因，不寻找克服困难的办法而是设法回避困难，难道不妨碍对相对论的深入理解吗？想出的回避办法越是看似十分巧妙、十分精彩、十分高深，造成的负面影响就越严重。我们之所以对现代解发表点看法就是这个缘故。

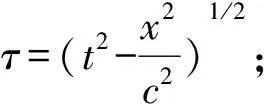
现代解流行之前有一种解与它很相似，也许它就是由这种解演变而来的。简单讲，这种解也可以用一句话表述：固有时是不变量。对于这种解我们曾作过评论[2]。这里顺便再强调一点，固有时是不变量不能确保可以解决时钟佯谬，例如讨论过程中会出现时钟读数的负增量这一离奇的结果，就是一个很难处理的问题。

引力理论方面著名的物理学家FOCK V的时钟佯谬解，也与现代解很相似[6]。他做了一个实例，可惜是个近似解，而且只做了一半，人们最关心的另一半他略去了，很让人失望。他不认为讨论时钟佯谬有很大价值。他之所以讨论它,是由于它受到了非常广泛的关注而且有些解是不能令人满意的,然而十分遗憾的是,他的解基本上没有引起人们的兴趣。