经济领先指数构建及对资产配置的影响

周 亮，周楷奇

（1.湖南财政经济学院 财政金融学院，湖南 长沙 410205；2.郑州大学 国际学院，河南 郑州 450011）

一、引言

经济周期是由经济中主要宏观变量的周期变化导致的，这些变量变动带来的基本面变动驱动着股票价格的变化，所以资产价格与经济状态变量之间有着天然显著的正向相关关系。Fama和French（1989）[1]发现经济变量对股票和债券的预期收益变动有着较好的解释。股价和宏观变量间的因果关系已经有很多成功的研究，研究的市场遍布全球，包括美国、英国、日本、新加坡等。Ferson和Harvey（1991）[2]研究发现与经济活动总体水平或者阶段状态有关的变量能够解释资产定价和预期股市收益之间的均衡关系。Mehr（2001）[3]指出公共政策对经济增长的影响可以通过股价来测量。Ibrahim和Aziz（2003）[4]研究发现宏观因素会通过影响预期现金流来影响股价。Charkravarty（2005）[5]也指出股价对宏观变量高度敏感。Frankel和Saravelos（2010）[6]指出外汇储备和真实汇率高估是经济危机预测中的两个最重要的领先经济指标。根据Dzikevičius和Zamžickas（2009）[7]对澳洲经济周期的研究发现，在经济结构失衡状态下，周期理论仍然能够很好地解释经济状态的改变。Ahemerkamp等（2012）[8]研究了多资产类别动量等策略的可预测性，发现商业周期指标具有很强的解释力。Cooper等（2016）[9]提出了价值和动量的全球宏观经济风险模型，并发现在各个资产类别的预期收益和实际平均收益之间存在有意义的关系。Hitendra和Jain（2018）[10]采用ADS指数和PMI指数来识别衰退周期，将经济周期的哑变量加入回归方程预测资产表现。

美林证券公司提出的投资时钟将宏观经济指标与资产轮动进行了较好地契合[11]。之后很多学者直接采用美林投资时钟对资产轮动策略进行设计和研究。Wang和Qu（2016）[12]采用GA-RS算法对经济周期进行分类，实证研究并发现了美林投资时钟在中国市场的适用性。苏民和逯宇铎（2011）[13]对美林投资时钟的周期阶段做了重新安排，用传统经济学的思维将滞胀剔除出第四阶段，而又建立一个新的非典型的经济周期配置模型把滞胀纳入，消除了美林投资时钟与传统经济学的不融合问题，扩展了其应用范围。张子能和董必焰（2012）[14]使用宏观经济数据确定完整的时钟周期，并对这一时期各主要资产的风险收益情况进行统计分析后发现，投资时钟理论对于我国资本市场的走势预期、资产配置决策以及风险管理等方面具有较强的实践意义。孙云等（2015）[15]以经济景气指数为基准进行数据分析后划分经济周期，并根据美林投资时钟来对比市场品种的收益，从而验证了其运用在中国的可行性。郜哲（2015）[16]和周亮（2018）[17]等学者运用美林投资时钟理论对我国的大类资产配置进行了实证研究，分析了我国宏观经济指标与成熟经济体的不同，指出投资时钟原理在我国实践应用中采取国家统计局的领先和滞后指数来划分经济周期更符合我国经济的特点。王健辉等（2018）[18]利用光谱利率和流动性指标拓展了投资时钟分析框架，并给出了不同广谱利率和流动性环境下的资产配置建议。总体来看，大部分学者的研究都支持宏观经济指标尤其是经济领先指标能够对资产配置提供富有意义的指导。

常用来构造经济领先指数的源指标包括股市指标、宏观流动性、经济各组成部分的产销数据等。股市常被看成是宏观经济的晴雨表，但是我国A股市场的政策敏感性较为明显，而中国香港股市由于市场化程度更高，且很多内地的股票都选择在中国香港上市，因此很多学者（包括统计局的宏观经济景气指数）都将恒生指数的月度收益率作为经济领先指标的源指标。流动性对宏观经济的影响是重要且关键的，当经济不景气的时候，管理当局往往会选择增大流动性的供给力度，从而刺激居民消费和企业投资，并带动经济重回增长的轨道；相反，当流动性收紧时，往往就是防止经济过热的起点，因此流动性是一个非常有效的经济领先指标。可以从数量和价格两个角度对流动性进行判断，M2同比增长率能够较为有效地衡量市场上的流动性，当前利率水平、期限利差及信用利差等利率指标则是衡量流动性价格的常用指标。除此以外，产品销售率、货运量、房地产开工等实体经济指标也对宏观经济有一定的领先性，产销率和货运量直接反映了实体经济的运行状况，房地产则是大部分国家的支柱产业，其带动了上下游几十个行业的发展，因此这几个指标可以直接反映出实体经济所面临的境况，能够对宏观经济有一定的引领作用。PMI指标作为统计局定期发布的反映实体经济的综合指标，更是常被用来预判经济增长的发展趋势。除此以外，消费者信心水平等指标也常被用来预判宏观经济的发展。

目前常用的经济领先指数包括国家统计局公布的宏观经济景气指数先行指数以及OECD中国领先指数等，但是这些指数公布的时间往往较慢，一般都要滞后于实际经济2个月时间以上。考虑到资本市场瞬息万变，过慢的指标对投资实践的指导意义大打折扣，因此本文拟借鉴这些领先指数的指标选取方法及合成方法，自行构建能够更及时反馈经济信息的领先指数，并对其经济预警能力及资产配置指导能力进行详细检验。

相对于其他研究经济指标及资产配置的文献，本文的可能贡献在于：第一，本文借鉴常见的经济领先指数构造方法，构造了更敏锐的经济领先指标，同时通过跨期相关检验、脉冲响应分析等多种方法检验了经济领先指标对宏观经济的领先性；第二，详细考察了多种信号分解方法在提取经济领先指标趋势项时的有效性，不仅为本文经济领先指标的区制划分奠定了基础，也是信号分解理论实际应用过程中的有益探索；第三，将经济领先指标与资产配置及股市风格轮动结合起来，在验证经济领先指标对资产配置及风格配置有效性的同时，也拓展了资产配置和投资组合理论的应用边界。

二、研究设计

（一）经济领先指数构造方法

常见的经济领先指数均是采用对宏观经济具有一定领先性的指标，并利用不同的加权方法进行合成。为了检验不同指标对宏观经济的领先能力，我们采用跨期相关系数进行分析，计算公式如式（1）所示：

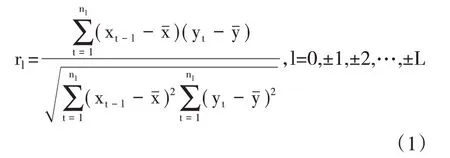
其中，l表示超前或滞后的期数，l取负数时表示超前，取正数时表示滞后；L是最大滞后期数，nl是数据取齐后的数据个数。通过观察跨期相关系数的大小及显著性，就可以判断出所选指标是否对宏观经济具有领先性，并利用具有领先性的经济指标加权得到最终的经济领先指数。常见的加权方法包括等权、主成分以及熵权等方法，考虑到熵权法能够更好地利用到变量本身的不确定性，且不确定性对于经济本身的波动具有较强的预见能力，因此采用熵权法对不同指标进行加权，具体计算步骤如下：

（二）信号降噪

为了考察经济领先指数对资产配置的影响，需要对指数进行降噪，以防止状态切换太频繁导致更多的交易成本及错误信号。常见的降噪方法包括HP滤波、EMD经验模态分解等，Hamilton（2018）[19]指出采用自回归的方式对数据降噪，可以避免其他模型可能带来的虚假信号。基于此，本文采用这三种方法来对构造的经济领先指数进行降噪。

（1）HP滤波法。

HP滤波是最常用的降噪方法，将变化不定的时间序列数据中具有一定变化趋势的平滑序列分离出来，将时间序列分为周期性波动数据和趋势要素数据。该方法广泛应用于宏观经济的趋势分析中。计算方法如式（2）所示：

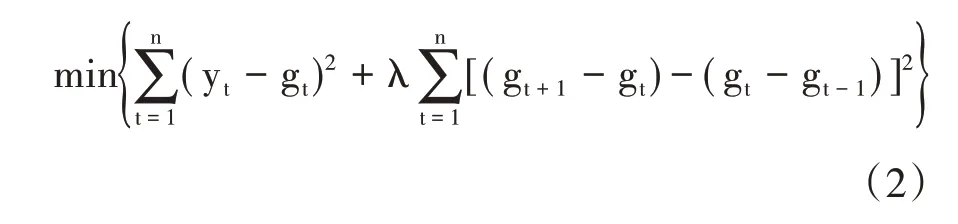
其中，yt为原始序列，gt为提取出来的趋势项。λ为平滑系数，λ越大，则gt越平滑，当v趋向于无穷大时，gt趋向于一条直线；λ越小，gt越趋向于yt，当λ为0时，gt就是yt。

（2）EMD经验模式分解法。

EMD是Huang等（1998）[20]开发的一种非线性、非平稳数据处理方法，它假定数据根据其复杂性可能同时存在多种振荡模式，具体计算步骤如下。第一，确定时间序列x(t)的所有极大值和极小值。第二，用三次样条插值生成其上下包络emin(t)和emax(t)。第三，计算上下包络的逐点平均值m(t)=(emin(t)+emax(t))+/2。第四，将x(t)和m(t)之差定义为d(t)=x(t)-m(t)。第五，如果d(t)是IMF，则将d(t)表示为第i个IMF，并用残差r(t)=x(t)-d(t)替换x(t)，第i个IMF通常表示为ci(t)，如果d(t)不是IMF，则用d(t)替换x(t)。第六，重复步骤一至五，直到残差项满足某种停止标准为止。

EMD往往分解出来的IMF信号比较多，如果对每个信号进行建模的话，无疑会加大计算机的运算难度，从而导致计算时间过长。因此，借鉴Zhang等（2008）[21]的方法，将所有的IMF合成高频和低频两个部分，实现信号的重构。具体计算步骤为：第一，计算每个成分（残差项除外）的c1(t)到ci(t)之和的平均值；第二，使用T检验确定均值显著偏离零的i；第三，在均值发生突变的变化点，就使用IMF从该位置进行部分重建，分别合成低频部分和高频部分，即用c1(t)至ci(t)合成高频部分，用ci+1(t)至cN(t)合成低频部分。

（3）Hamilton方法。

Hamilton（2018）[19]指出如HP等降噪模型可能带来的虚假信号，因此在对经济序列进行降噪时，采用自回归的模型形式能够更好地提取真实的趋势序列，具体模型形式如式（3）所示：

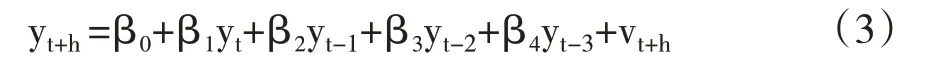
其中，yt为原始序列，h为领先阶数；vt为回归残差，即为波动项；趋势项则可以表示为yt-vt。Hamilton（2018）[19]指出如果采用月度数据，将h设定为48比较好；如果采用季度数据，将h设定为16比较好，即采用4年的样本进行回归。

后续分析，本文将采用这三种方法对经济领先指数降噪，同时利用一定的方法和技术比较三种降噪方法的优劣。

（三）马尔科夫区制转换模型

马尔科夫区制转换模型可以对经济领先指数所处的阶段进行划分，从而对我们的资产配置提供前瞻性信息。马尔科夫区制转换模型的形式如式（4）—式（8）所示，假定变量满足r阶自回归、具有N种区制，假设每种区制下有不同的均值和方差，则有：

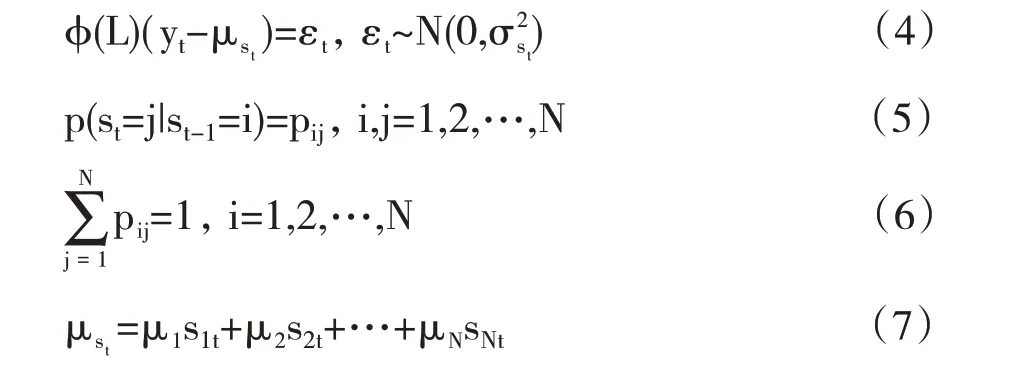
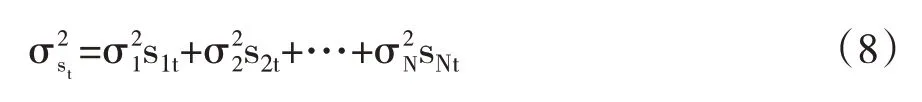
其中，yt为所研究的时间序列，φ(L)为滞后算子多项式，st表示存在M种状态的马尔科夫区制转移变量，st=1,2,…,M，pij为转移概率，μst和σ2st分别为st状态下的均值和方差。采用Hamilton滤波方法来推断转移概率，进而运用极大似然法可以求出各参数的估计值。本文采用变量的一阶自回归来构造两区制马尔科夫转换模型AR(1)-MS(2)，具体模型形式如式（9）所示，其中yt表示经济领先指数的时间序列：

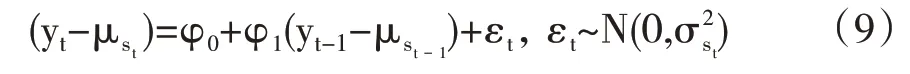
（四）数据描述及统计

本文借鉴其他学者的研究，选定了9个可能对宏观经济具有领先性的指标，包括恒生指数月收益率（Stock）、产品销售率同比变化（Sale）、PMI同比（PMI）、M2同比增长率（M2）、房地产开工率同比变化（House）、货运量同比变化（Freight）、消费者预期指数（ICE）、期限利差（Term）以及信用利差（Credit）等，样本区间为2005年1月至2021年6月的所有月度数据，所有数据均来自Wind数据库，对于缺失数据采用线性平滑方法进行补齐。对变量的描述性统计分析如表1所示。从AR(1)和AR(6)可以看到，大部分经济变量的自相关性均很强，如M2的6阶自相关系数仍然高达0.83，股票收益率和产品销售率同比变化的自相关性相对较弱，尤其是股票收益率，其6阶自相关系数甚至为负值。

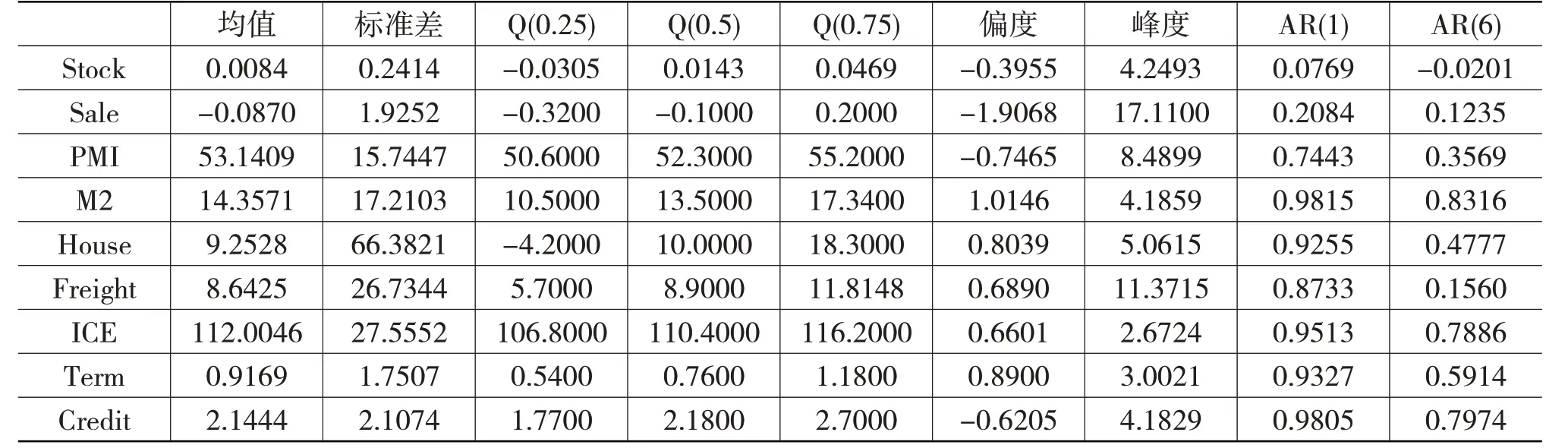
表1 变量描述性统计分析

三、实证检验

（一）变量筛选

虽然本文按照经济逻辑以及前期研究，选用了9个经济领先指标，但是这9个指标对于经济的领先作用仍然需要提前进行分析，以筛选出更合适的指标对经济的变动提前发出信号。表2报告了9个变量之间的相关系数，可以看到，绝大部分指标间具有相关关系，相关性最高的是货运量与房地产建设，其相关系数高达0.55，两个利率指标与部分经济指标间的相关系数显著为负，如二者与货运量的相关系数均为-0.2，且在1%水平下显著。除此以外，其他大部分指标间的相关系数均为正。总体来看，本文所选的9个经济指标间存在着一定的互动关系，但是相互之间也存在着较大的差异，将这9个指标进行综合，可以有效整合多方面的市场信息，从而可以对宏观经济形势进行更全面的判断。

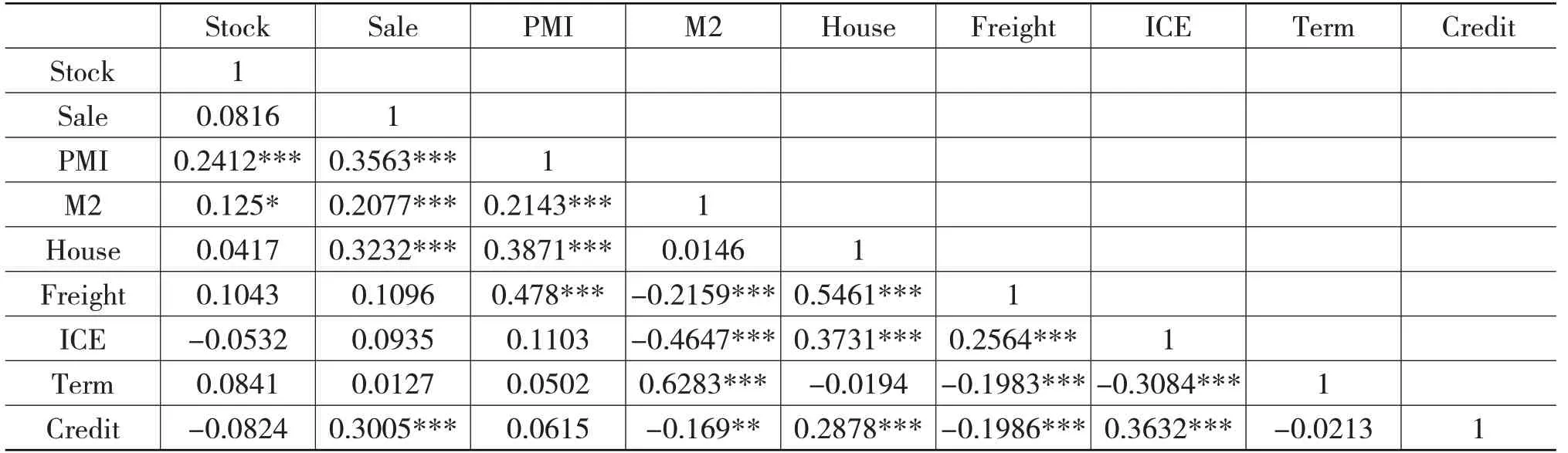
表2 变量相关性检验

利用跨期相关检验，本文考察了9个经济指标与工业增加值（IVA）之间的领先滞后关系，结果如表3所示，其中行标题代表领先或滞后的阶数，“-12”表示每列所代表的经济指标领先工业增加值12期，“0”表示经济指标与工业增加值同期，“12”表示经济指标滞后工业增加值12期，其他以此类推。表中阴影的数字代表经济指标与工业增加值相关性最高的时期，可以看到，股票市场收益率、M2以及期限利差分别领先工业增加值2个月、6个月和10个月；产品销售率、PMI及房地产开工率对工业增加值具有一定的领先性，并在同期达到最高的相关系数；货运量、消费者预期指数以及信用利差则分别滞后于工业增加值3个月、12个月和12个月。因此在构造最终的经济领先指数时，货运量、消费者预期指数以及信用利差三个指标应予以剔除，同时为了增加信息的全面性，最终选择了股票市场收益率、M2、期限利差、产品销售率、PMI及房地产开工率6个指标进行分析。

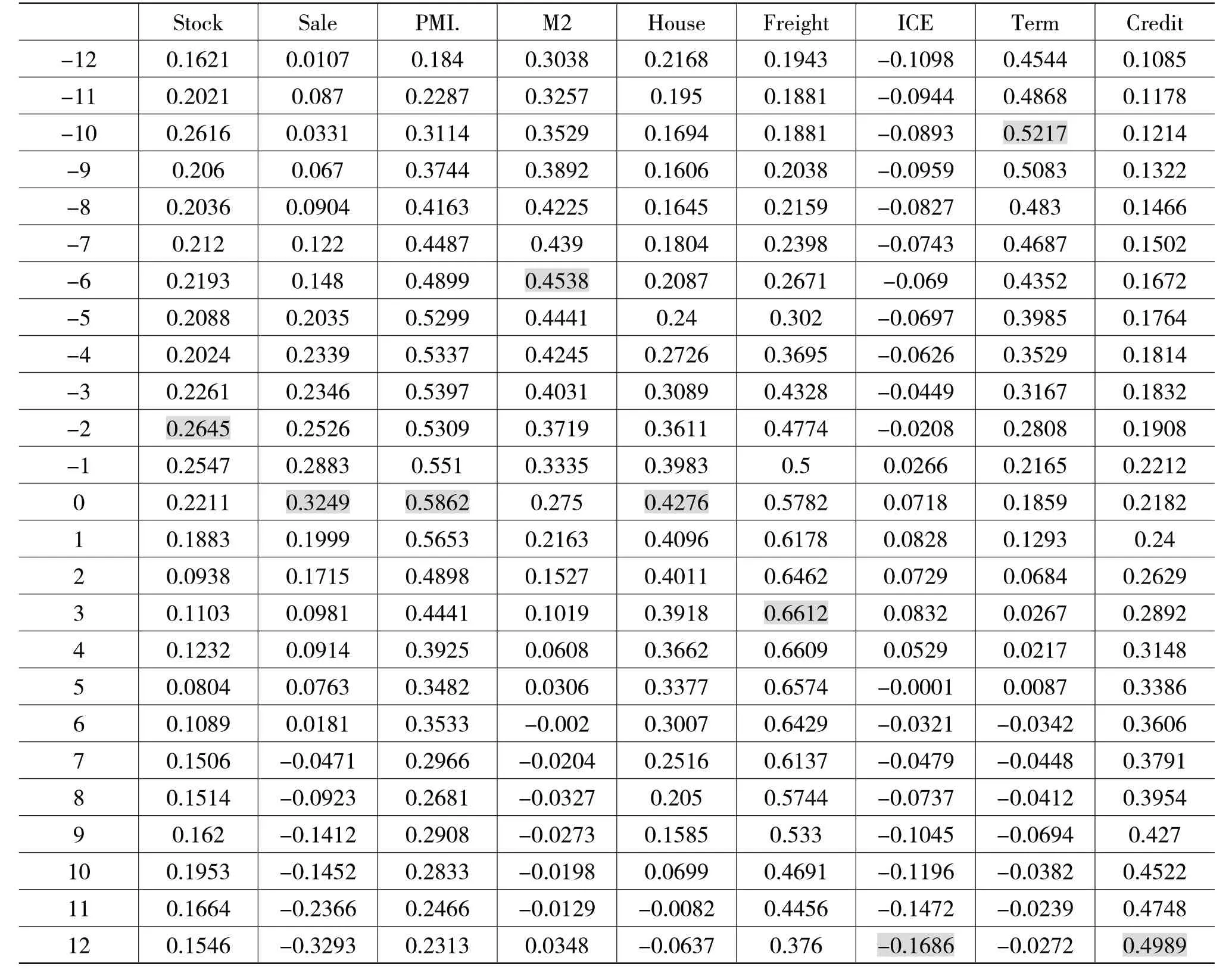
表3 与IVA的跨期相关性检验

（二）经济领先指标分析

本文首先对所有的指标进行X-12ARIMA季节性调整，再进行归一化处理，考虑到不确定越高的指标对宏观经济的影响往往越大，因此采用熵权法来确定各指标的权重，从而合成最终的经济领先指标（CLI），结果如图1所示。从图中可以看到，经济在样本区间出现了3个明显的低点，分别是2008年10月、2014年12月以及2020年2月。2008年是受美国次贷危机的发酵，我国经济于2008年下半年快速回落，大批农民工返乡，出口负增长，2008年11月进出口总值同比下降9%，GDP在2008年第4季度下降4个百分点，经济面临“硬着陆”的风险。在此之后，中国政府果断推出扩大内需、促进经济平稳增长的相关举措，抑制住了经济下滑的趋势，2009年GDP增长9.4%，经济领先指标也在2009年出现了大幅攀升，并于2009年11月达到阶段性峰值。2015年是中国经济运行相对艰难的一年，1月份CPI远低于市场预期，达到2009年11月来最低水平，PPI同比下降4.3%，为2009年来最大跌幅；中国楼市也面临着硬着陆风险，房价从2014年下半年开始出现了下滑；而股市更是出现了剧烈的波动，2015年6月15日，上证指数触及5178的高点后掉头向下，千股跌停频现，上证指数在2016年初达到2638的低点；整个2015年GDP增幅为6.91%，自1991年以来首次跌破7%。而经济领先指数在2014年12月已经发出了经济减缓的信号。2020年2月的低点则是受新冠肺炎疫情影响，全球经济近乎停滞。2020年1—2月份我国规模以上工业企业利润骤降38.3%；一季度货物贸易进出口总值比去年同期下降6.4%，其中出口下降11.4%、进口下降0.7%、贸易顺差减少80.6%；一季度我国GDP增速下跌至-6.8%。因此总体来看，CLI指标可以对我国宏观经济的动态走势进行较好的拟合，且具备一定的前瞻性，更细致的数理分析详见下文分析。

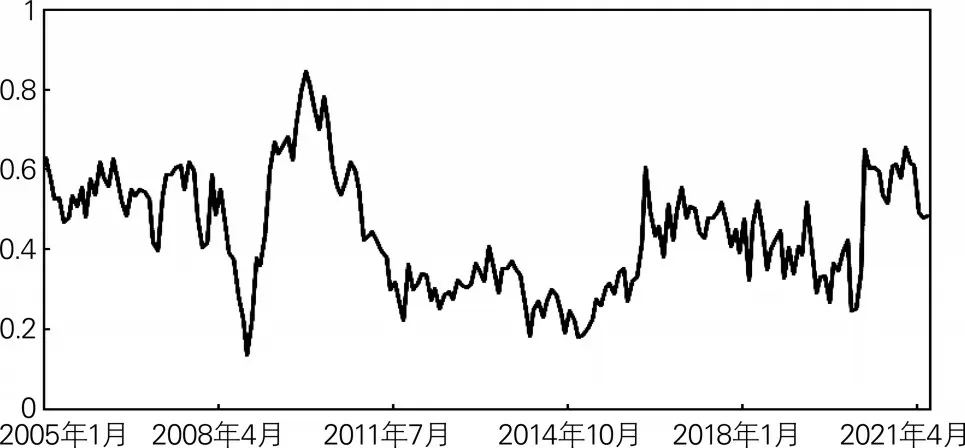
图1 CLI走势图

为了观察CLI对宏观经济的领先滞后关系，我们同样对CLI与IVA进行了跨期相关性检验，结果如图2所示，纵坐标表示跨期相关系数，横坐标表示CLI对IVA的领先或滞后关系，“-12”表示CLI领先IVA指标12个月，“12”表示CLI滞后IVA指标12个月。从图中可以看到，CLI指标对IVA具有较强的领先作用，在领先12个月时的相关系数就高达0.43，并在领先5个月时相关系数达到最大值0.62，说明所构建的CLI指标对IVA至少领先了5个月以上，进一步验证了CLI指标的有效性。

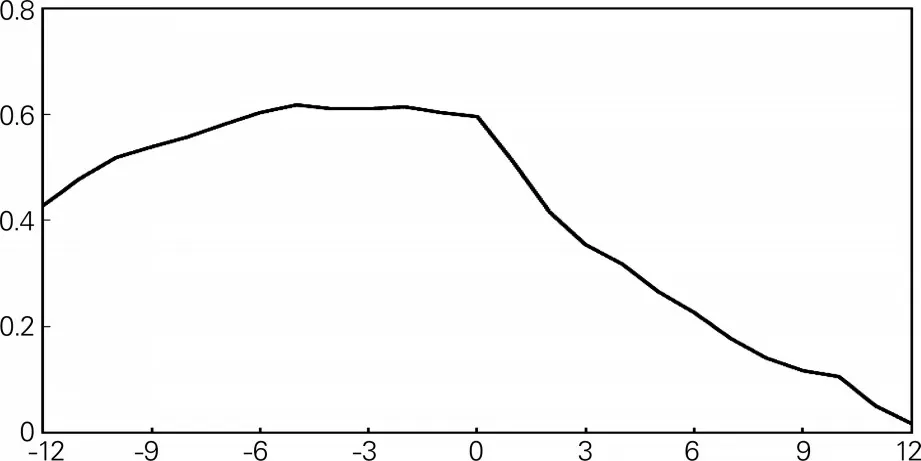
图2 跨期相关性检验

（三）脉冲响应分析

为了更进一步观察CLI对宏观经济的影响，本文构造了VAR模型并进行脉冲响应分析，所选变量依次为IVA、Invest、Consume、Import、CPI、CLI，其中Invest为固定资产投资同比增速，Consume为零售品消费总额同比增速，Import为进出口总额同比，CPI为通货膨胀率。将CLI置于变量之后，可以更清晰地判断出CLI对宏观经济的影响，因为在VAR分析过程中，越靠后的变量影响往往越小。VAR模型根据AIC准则选择滞后4阶。图3报告了IVA与CLI的相互作用，其中左图为CLI一个单位冲击对IVA的持续影响力，右图为IVA一个单位冲击对CLI的持续影响力。可以看到，CLI的单位冲击对IVA产生了显著的影响，且这种影响是持续的，在第8期达到最大，并一直持续到10期以后；而IVA的单位冲击对CLI的影响却较小，仅持续了3期就转到了0及以下。因此可以说明，CLI对IVA具有显著的持续的作用，这种作用表现出来就在于其经济领先性，反之IVA却对CLI作用甚微。

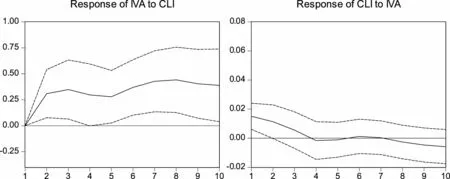
图3 CLI与IVA的脉冲响应分析

图4报告了CLI对其他宏观经济变量的脉冲响应分析结果，可以明显看到，当给CLI一个单位冲击后，对投资、消费、进出口以及通货膨胀均有显著的持续影响，且除了对投资的影响在第3期后基本维持均衡外，对消费、进出口及CPI的影响均随着期数的增加而不断累积。图4的结论不仅进一步肯定了CLI对宏观经济的领先性，而且这种领先性不仅表现在对工业生产上，对于经济的三驾马车以及物价走势，均有较强的领先性。因此综合图2至图4的研究结论，本文得出以下结论，CLI指标是一个有效的经济领先指标，并且由于所选的部分变量公布的时间点较为靠前，能够及时对宏观经济的变化进行预先判断。

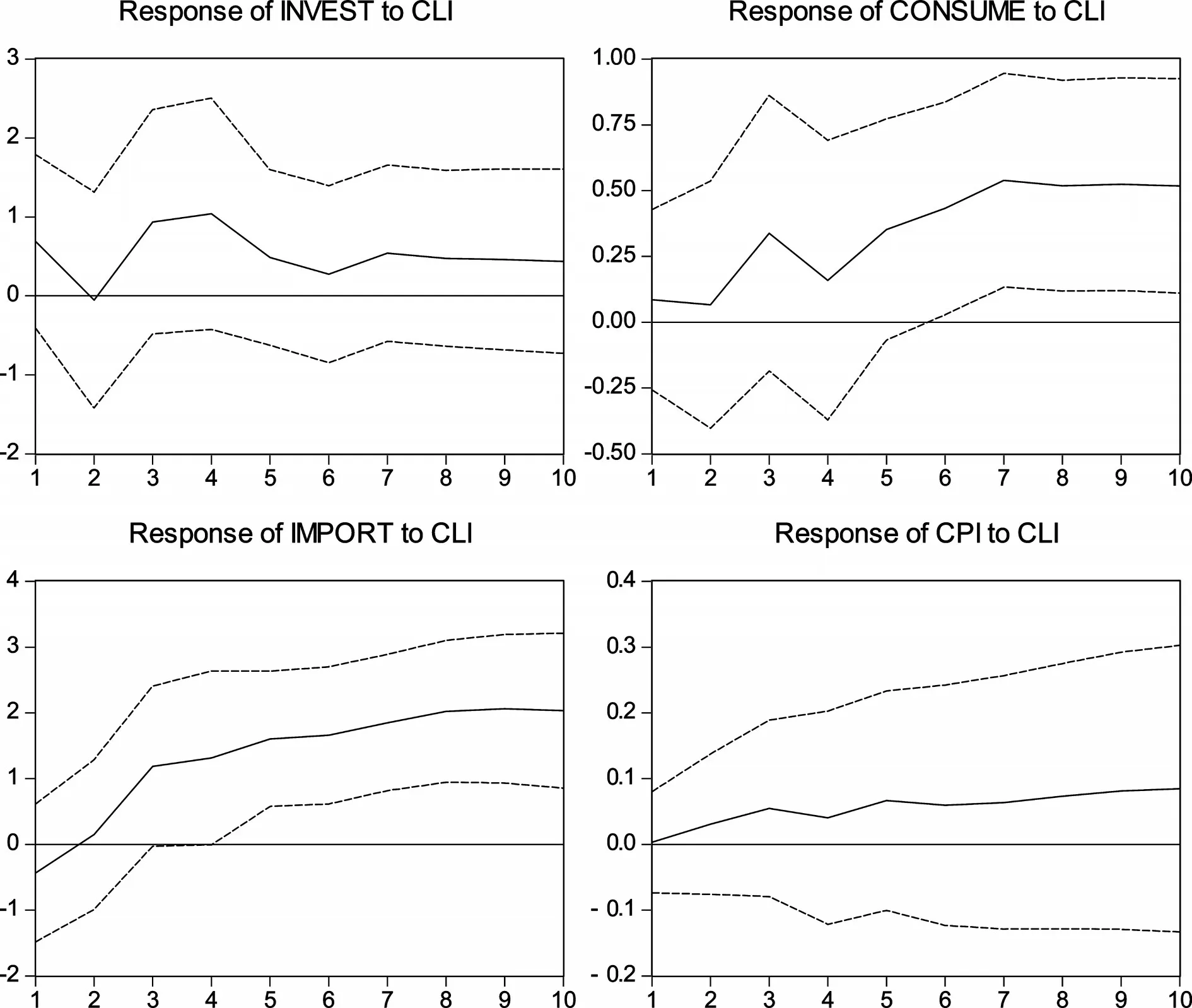
图4 脉冲响应分析

（四）对资产配置的启示

1.回归分析

本部分重点考察CLI指标对资产配置的影响，选择了三种资产配置方式进行分析，分别是股票与债券的轮动配置，其中股票采用Wind全A指数衡量，债券采用中证全债指数衡量；参考Fama和French（1993）[22]的研究，考察了两种股票风格的轮动配置，其一是小盘股与大盘股的轮动（对应FF三因子中的规模因子），分别采用巨潮小盘股指数和大盘股指数衡量；其二是成长股与价值股的轮动（对应FF三因子中的估值因子），分别采用巨潮成长股指数和价值股指数衡量。表4报告了CLI对这些指数相对收益的回归结果，控制变量采用了投资、消费、进出口以及物价指数，CLI及所有的控制变量均取滞后一期。从表中回归结果来看，所选变量对不同价格指数的比值具有一定的回归效果，调整R2分别达到0.3、0.13和0.34。CLI对三个价值指数的拟合效果较好，其中对股票/债券及成长/价值比值的回归系数均显著为正，对小盘/大盘比值的回归系数显著为负。这说明在CLI处于上升趋势时，配置股票、大盘股及成长股，相对于债券、小盘及价值股更优。

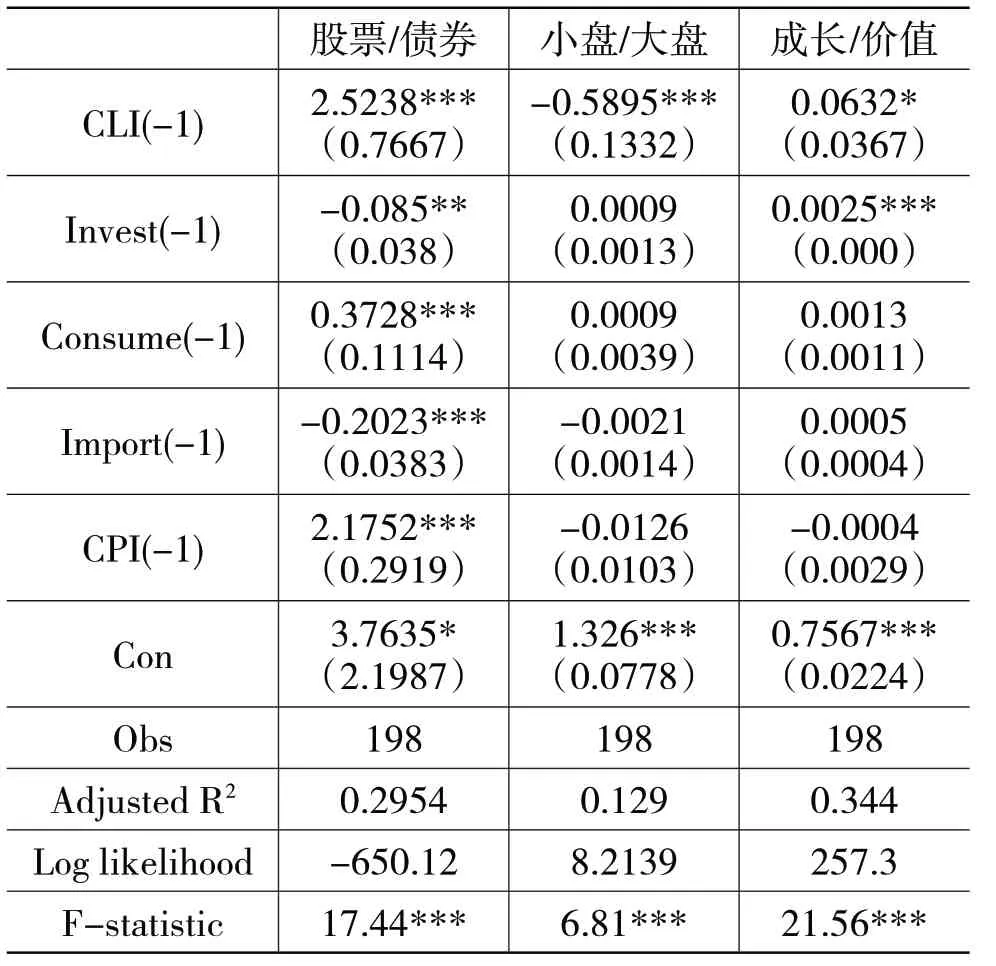
表4 CLI对资产配置的回归分析

2.CLI降噪

我们进一步从实际投资绩效的角度考察CLI对资产配置的影响，具体而言需要先将CLI区分为上升阶段和下降阶段，并在不同的阶段配置不同的资产类别。在对CLI进行阶段划分时，常见的方法包括“谷—峰”法及马尔科夫区制转换方法。考虑到“谷—峰”法更多的是从事后角度进行判断，实际投资过程中难以进行操作，因此采用马尔科夫区制转换法进行阶段划分。但是由于原始数据中包含了大量的噪声，如果直接采用原始数据进行分析，会导致状态变换过于频繁，从而增大交易成本以及发出太多的虚假信号，因此在进行马尔科夫区制转换模型构建前，先对原始数据进行降噪。

常见的降噪方法包括HP滤波、EMD经验模态分解等，Hamilton（2018）[19]指出采用自回归的方式对数据降噪，可以避免其他模型可能带来的虚假信号。基于此，本文采用这三种方法进行降噪，并挑选最合适的降噪方法进行进一步分析。

采用两种方法进行判断：一是观察降噪序列与原序列的关系，拟合得越好的模型相对更优；二是我们对原始序列分阶段拟合，观察真实趋势序列与实时趋势序列的差异。具体而言，分别进行全样本降噪（2005年1月至2021年4月）及部分样本降噪（2005年1月至2020年2月），并观察2005年1月至2020年2月这段时间内两种降噪方法所提取趋势项的差异。

图5报告了研究结果，其中Panel A是三种降噪后的趋势序列与原始CLI的走势图。可以看出，Hamilton方法效果最差，基本为一条水平直线，HP的效果较好，与原始CLI拟合较好，且能较好地识别出拐点，EMD变化相较HP要慢，能够识别出更大级别的趋势。Panel B至Panel D分别是HP、EMD及Hamilton降噪法的部分样本比较情况。可以看出，HP降噪法除了存在一定的端点效应，全样本与分样本拟合结果基本一致；EMD降噪法同样存在着明显的端点效应，但是两个样本存在着一定的偏差，不如HP拟合得好；Hamilton全样本与分样本间的拟合曲线完全不一致。因此综合来看，用HP进行降噪的效果要优于其他两种方式，虽然存在着一定的端点效应，但是一方面可以将尾部几个数据剔除，另一方面可以通过机器学习等方法对尾端数据进行拟合等方式的处理，以减小端点效应对数据处理的影响。

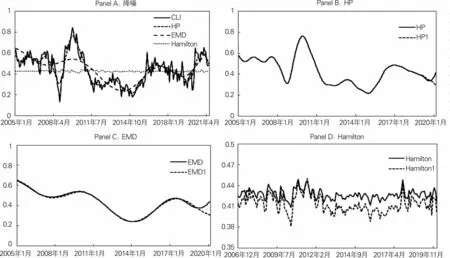
图5 降噪结果分析

3.马尔科夫区制转换

我们建立两区制一阶自回归马尔科夫转换模型MS(2)—AR(1)来对HP滤波后的CLI序列进行分析，回归结果如表5所示。可以看出，MS-AR模型较好地将CLI区分成两区制，其中区制1代表低风险，即风险不断下降阶段，对应图6的灰色区域部分；区制2为高风险区域，即风险不断上升阶段，对应图6的白色区域部分。两区制的转换概率分别高达0.96和0.92，说明高低区制非常稳定，相互转换的概率较小，期望持续时间（用式1/（1-P）计算）分别达到25个月和12个月。从图6绘制的区制转化图可以看出，高低区制基本上较好地拟合出了CLI的上升阶段和下降阶段，同时又规避了原始序列不断波动的特性，避免了区制的反复切换。且从图6可以看到，进入2021年，我国经济开始进入下降区间。

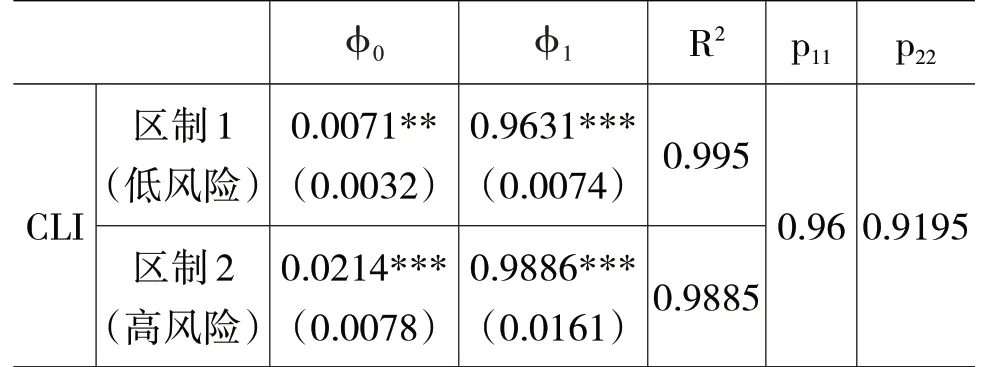
表5 马尔科夫区制转换回归结果

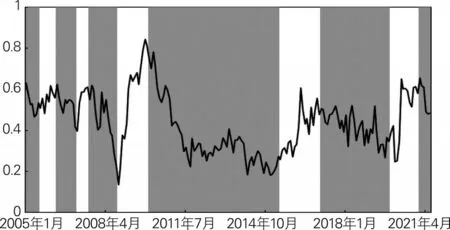
图6 马尔科夫区制划分

4.资产配置绩效分析

根据表4的回归结果以及图6的CLI区制划分，构造资产配置择时策略：对于股债轮动配置，在CLI上升区制配置股票资产，在CLI下降区制配置债券资产；对于规模轮动配置，在CLI上升区制配置大盘股，在CLI下降区制配置小盘股；对于价值轮动配置，在CLI上升区制配置成长股，在CLI下降区制配置价值股。考虑到宏观数据公布的滞后性，本文对所有的CLI均滞后一期，即依据上一期CLI所处的区制来判断本期的资产配置。

表6报告了资产轮动策略及对应的原始指数序列的投资绩效，图7报告了资产轮动策略以及对应指数的净值曲线。可以看到，对于股债轮动而言，策略可以实现12.93%的年化收益，远高于Wind全A指数的9.52%，且波动率及最大回撤均低于单独配置Wind全A指数。从图7中Panel A也可以看出，股债轮动策略最终净值达到7.59，远高于Wind全A指数的4.56；对于规模轮动而言，策略可以实现15.6%的年化收益，高于小盘股的13.58%和大盘股的11.91%，且其风险与大盘股持平，低于小盘股的32.64%，因此轮动策略的夏普比率达到0.43，高于小盘股的0.32和大盘股的0.3。从图7中Panel B可以看出，规模轮动策略最终净值达到11.21，远高于小盘股指数的8.35；对于价值轮动而言，策略可以实现14%的年化收益，高于成长股的12.83%和价值股的11.73%，策略夏普比率为0.36，高于成长股的0.32和价值股的0.29。从图7中Panel C可以看出，价值轮动策略最终净值为8.88，高于成长指数的7.48。因此，综合来看，本文所构造的CLI指标能够对宏观经济进行较为有效的预警，且经过HP-MS划分后的区制，能够对投资者的投资实践进行一定的指导。

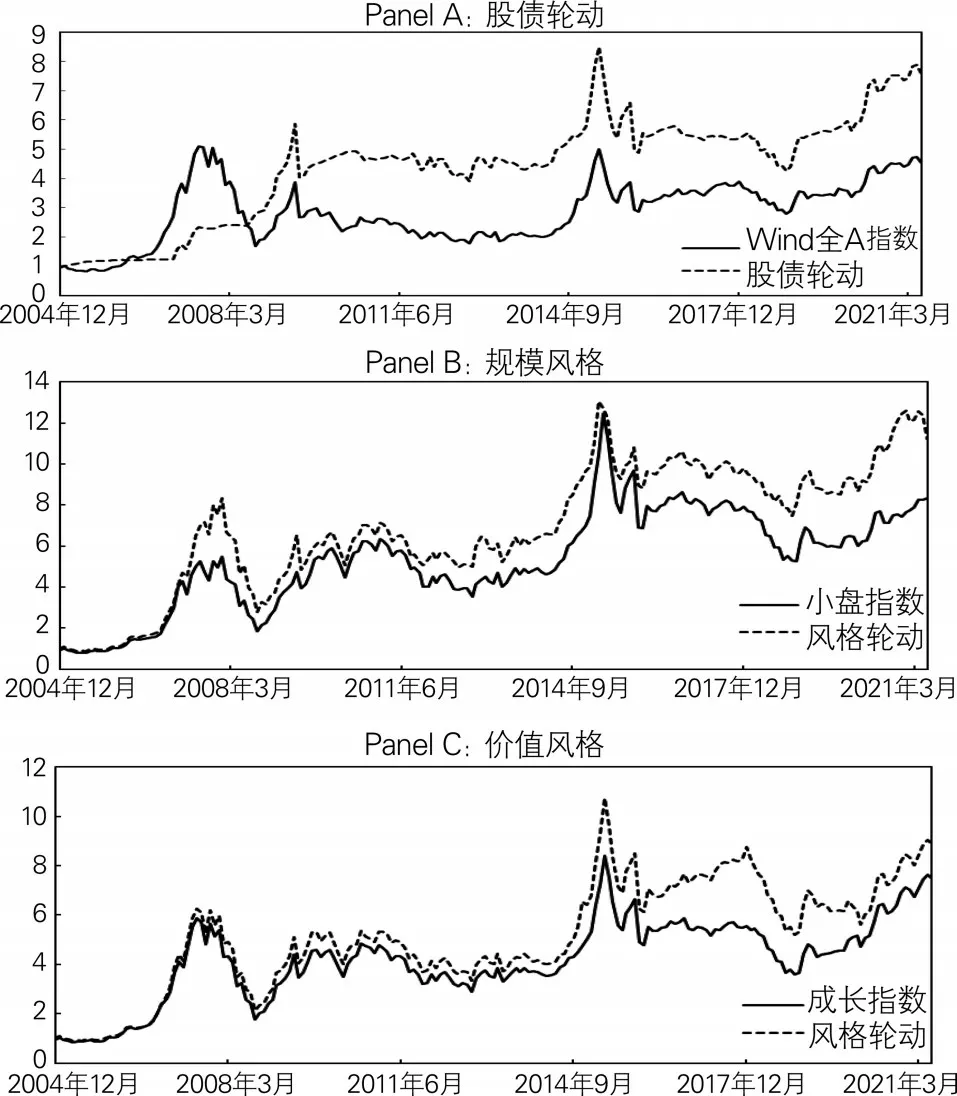
图7 资产配置策略净值曲线

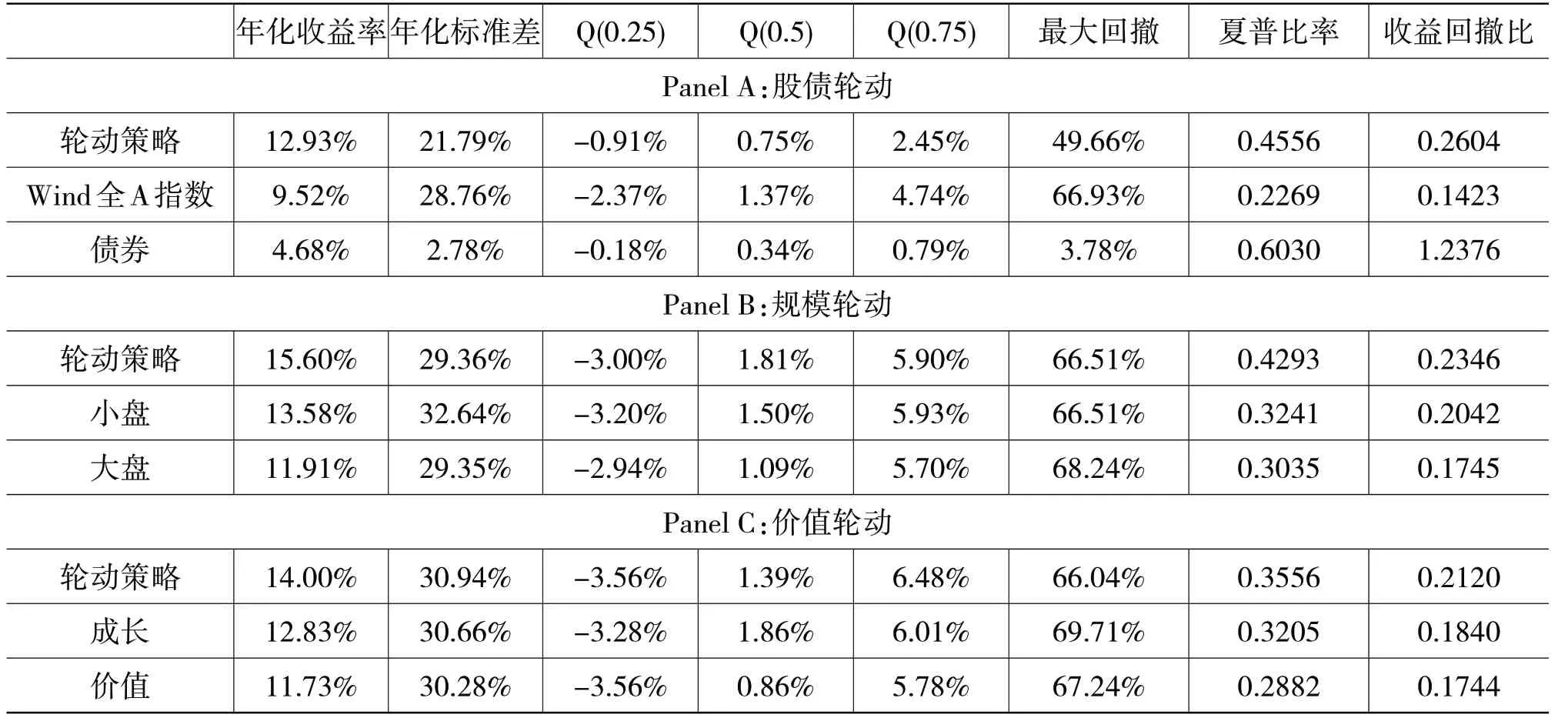
表6 资产配置择时绩效

四、结论与讨论

选取2005年1月至2021年4月恒生指数收益率、产品销售率同比变化、PMI同比、M2同比增长率、房地产开工率同比变化、货运量同比变化、消费者预期指数、期限利差以及信用利差的同比数据构造我国宏观经济的领先指数。首先通过跨期相关检验剔除对经济增长指标不具备领先性的指标，其次利用熵权法对剩余的指标进行加权，并研究了经济领先指数（CLI）对宏观经济的预测能力以及对资产及股票风格配置的影响。结果发现：CLI指标领先了工业增加值5个月以上，且脉冲响应分析发现，CLI对工业增加值、投资、消费、出口以及物价指数等宏观经济指标均有持续稳定的影响，相反工业增加值等指标对CLI的影响则非常短暂；HP滤波能够更好地提取CLI的趋势项，并用马尔科夫区制转换模型对CLI趋势项进行状态划分，发现CLI对股债配置以及股票风格配置可以起到非常有益的指导作用，股债轮动、规模轮动以及价值轮动策略在样本区间分别可以获得12.93%、15.6%及14%的收益率，远高于单独对两项资产的买入持有配置以及等权配置。综合来看，本文构造的CLI指标不仅能够对宏观经济进行提前预判，而且能够对资产配置实践具有较强的指导意义。

本文的研究结论不仅是对经济预测理论及资产配置理论的有力补充，同时对于投资实践也具有较强的指导意义。

首先，部分指标确实具有较强的宏观经济预警能力。如本文最终选取的股市收益率、M2和期限利差等，通过适当的模型和方法将这些指标进行整合得到的经济领先指数，可以对经济状态的未来发展走势进行较好的预判，无论对国家大政方针的制定还是个人投资者投资策略的规划，都具有较强的指导意义。

其次，美林投资时钟在我国的投资实践中仍然具有较强的指导意义，对其应用的关键在于经济增长指标的准确选取。许多学者的研究均表明领先指数相对于GDP和工业增加值等实际经济增长指标可以更好地用来对经济周期进行划分，且由于经济指标公布的滞后性，领先指数可以部分规避该问题。在经济扩张期适当多配股票及大盘成长型股票，可以在提高投资收益的同时降低投资风险。

再次，我们所构造的基于经济领先指数的轮动虽然相对于简单买入持有单一指数具有一定的超额收益，但是风险和回撤仍然较大。这说明投资是一件复杂的系统工程，想通过单一指标实现投资绩效的显著改善是较为困难的，更适合的策略应该是将多种指标进行综合分析，同时借鉴大数据分析和人工智能等更复杂的系统性技术以提高预测的准确性。