爆炸冲击下水底隧道的动态响应及毁伤模式研究
杨广栋, 王高辉, 李 麒, 陆春华, 卢文波, 周俊汝, 赵金帅
(1. 三峡大学 湖北省水电工程施工与管理重点实验室,湖北 宜昌 443002;2. 武汉大学 水工岩石力学教育部重点实验室,武汉 430072; 3. 长江勘测规划设计研究院,武汉 430010;4. 江苏大学 土木工程与力学学院,江苏 镇江 212013)
为了缓解城市交通拥堵,促进城市间的相互协调发展,我国已建或在建一批重要的水底隧道,如图1(a)所示。如港珠澳大桥,是我国境内一座连接香港、珠海和澳门的桥隧工程,包含了6.7 km长的海底隧道,该海底隧道是国内首个海底沉管隧道,如图1(b)所示。港珠澳大桥是国家重器,其建设创下了多项世界之最,体现了我国的综合国力、自主创新能力以及勇创世界一流的民族志气。除此之外,还有广州珠江隧道,是我国大陆首次采用沉管法设计施工的大型水底隧道;目前正在论证的大连至烟台海底隧道,一旦建成,大连至烟台的通行时间将缩短至40 min,对东北的全面振兴、全方位振兴将发挥重要的推动作用,如图1(c)所示。

图1 水底隧道Fig.1 Underwater tunnel
水底隧道带来巨大益处的同时,也面临着越来越严酷的爆炸威胁。像生活生产中的一些意外爆炸,如易燃易爆品运输工具的爆炸(长江航道轮船意外爆炸,如图2(a)所示;山西晋济高速隧道爆炸,如图2(b)所示,战时遗留未爆炸弹的爆炸(长江打捞出二战期间遗留炸弹,如图2(c)所示等。还有越来越复杂的国际局势,使发生局部冲突和恐怖袭击的风险增大。一旦结构发生破坏,外部的水体将直接涌入隧道内部,给人员、车辆及设备等造成致命的打击。目前关于爆炸荷载作用下,隧道结构的动力响应研究主要集中在地表爆炸荷载或内部爆炸荷载[1-5]。如:Stolz等[6]采用模型试验和数值模拟相结合的方法,研究了内部爆炸荷载作用下隧道结构的抗爆性能;Kristoffersen等[7]研究了内部爆炸荷载作用下不同断面水下隧道的毁伤分布特征;赵跃堂等[8]分析了内爆条件下管片衬砌结构的变形和破坏规律,提出了一种在接头螺栓处添加柔性垫圈来降低与螺栓接触区域管片破坏程度的方法;章毅等[9]研究了地表炸药库爆炸对地铁隧道安全运行的影响;Mussa等[10]采用ALE(arbitrary lagrange euler)方法研究了不同当量地表爆炸荷载下箱型隧道的抗爆性能。

图2 隧道结构可能遭受的爆炸荷载Fig.2 Potential blast loads act on the tunnel
对于水下爆炸作用下结构的破坏特性研究主要集中在混凝土板柱、大坝、码头及船舶等结构。如:Yang等[11]研究了不同截面的钢筋混凝土柱在水下近场爆炸荷载作用下的损伤特性和动力响应;闫秋实等[12]讨论了水中近场爆炸作用下钢筋混凝土桩的毁伤效应;Zhao等[13-14]采用现场试验和数值模拟的方法,研究了水下接触爆炸荷载作用下钢筋混凝土板结构的毁伤分布特性;王高辉等[15-16]研究了水下爆炸冲击荷载下混凝土重力坝的破坏效应,分析了起爆距离、炸药当量、起爆深度、水深等因素对大坝毁伤分布特征的影响;李凌锋等[17]开展了不同爆炸荷载条件下沉箱重力式码头模型毁伤效应试验,得到了沉箱重力式码头模型在空中爆炸、水下爆炸以及结构内部爆炸后的毁伤模式;任鹏等[18]利用水下爆炸冲击波等效加载装置结合高速摄影技术,对铝合金圆板进行了水下冲击波加载试验,得到了气背固支圆板塑性大变形、中心拉伸撕裂和边界剪切破坏3种典型失效模式的动态响应历程;Ming等[19]采用SPH-FEM(smoothed particle hydrodynamics-finite element method)耦合的方法研究了水下接触爆炸冲击波对舰船结构的损伤特性。但关于水下爆炸荷载作用下水底隧道的动力响应及毁伤模式研究成果较少。
以某无覆盖层水底隧道为研究对象,通过构建水下爆炸全耦合模型,分析了水下爆炸荷载作用下水底隧道的毁伤发展过程;讨论了起爆距离及炸药当量对水底隧道毁伤模式的影响;得到了水下爆炸荷载作用下水底隧道的动力响应特性、毁伤机制及毁伤模式,可为水底隧道的抗爆设计和防护提供参考。
1 材料模型
1.1 混凝土
采用RHT(riedel-hiermaier-thoma)模型模拟混凝土结构在爆炸荷载作用下的损伤发展过程。该模型除了具有压力依赖性、应变速率敏感性和压缩损伤软化等特点外,同时引入了偏应力张量第三不变量对破坏面形状的影响,考虑了拉静水区和压静水区应变率敏感性的差异性。该模型中采用了弹性极限面、失效面及残余强度面作为3个控制破坏面以描述混凝土材料的初始屈服强度、失效强度和残余强度,混凝土相关参数如表1所示[20-22]。
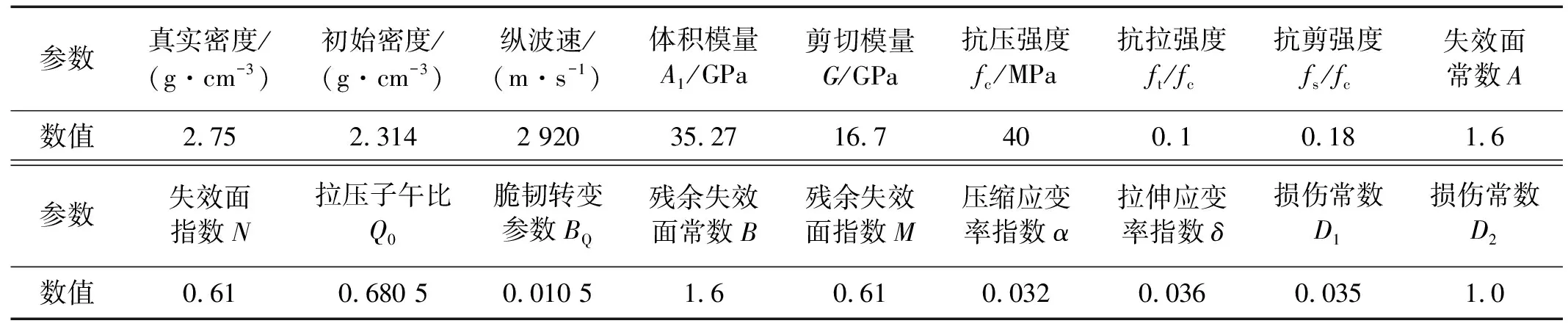
表1 混凝土RHT模型参数
RHT模型失效面方程为
(1)
(2)
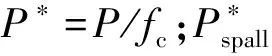
RHT本构模型的损伤定义为
D=∑(Δεp/εp,failure)
(3)
(4)
式中:D1,D2为损伤常数;εp,failure为失效应变;εf,min为最小失效应变。
1.2 炸 药
采用JWL状态方程描述爆炸中化学能产生的压力[23]
(5)
式中:P为爆轰压力;V为炸药爆轰产物的相对体积;E0=6.0 GJ/m3,ρ=1 630 kg/m3,D=6 930 m/s,Pcj=21 GPa,A1=373.77 GPa,B1=3.75 GPa,R1=4.15,R2=0.90,ω=0.35均为材料常数。
1.3 水
对于水体采用Polynomial状态方程[24]。
当水压缩时(μ>0),状态方程为
P=A1μ+A2μ2+A3μ3+(B0+B1μ)p0e
(6)
当水膨胀时(μ﹤0),状态方程为
P=T1μ+T2μ2+B0p0e
(7)
式中:P为水中压力;μ为压缩比,μ=ρ/ρ0-1;e为水的内能;ρ0为水密度,取1 g/cm3;A1=T1=2.2×106kPa;A2=9.54×106kPa;A3=1.46×106kPa;B0=B1=0.28;T2=0。
1.4 空 气
空气采用Ideal Gas状态方程
(9)
式中:ρ0为空气初始密度,取1.225 kg/m3;E为空气初始内能;γ为材料常数,取1.4。
1.5 钢 筋
在爆炸荷载作用下,需考虑应变硬化、应变率硬化等对钢筋性能的影响。采用Johnson-Cook模型描述钢筋的动力特性,该模型将屈服应力[25]定义为
(9)
TH=(T-Troom)/(Tmelt-Troom)
(10)


表2 钢筋材料参数表
2 爆炸耦合模型及模型验证
为了验证爆炸荷载作用下钢筋混凝土材料模型及耦合计算方法的可靠性,对钢筋混凝土板空中接触爆炸试验进行模拟再现,如图3(a)所示。理想的方法是利用水下爆炸荷载作用下钢筋混凝土结构的试验数据来校准数值模型。然而,公开的文献中关于水下爆炸荷载下钢筋混凝土结构的动力响应试验数据较少。同时对于钢筋混凝土结构水下爆炸试验很难在短时间内进行。但本文采用的流固耦合计算方法及钢筋混凝土材料模型都是与空中爆炸试验一致的。因此,基于空中爆炸试验数据校正后的数值模型可以用于模拟水下爆炸荷载作用下的隧道响应。该试验中采用的钢筋混凝土板的尺寸为1 000 mm×500 mm×60 mm。炸药TNT当量为210 g,纵向钢筋和横向钢筋的直径均为6 mm,如图3(b)所示。混凝土抗压强度为38 MPa,钢筋的屈服强度为400 MPa,弹性模量为210 GPa。
基于Lagrange-Euler耦合方法建立了混凝土板空中接触爆炸试验数值模型,如图3(c)所示。炸药和空气均采用Euler单元,混凝土材料使用Lagrange单元,钢筋采用Beam单元。采用流固耦合的方法描述空气与混凝土材料之间的相互作用,钢筋与混凝土材料之间的相互作用通过节点固接的形式实现。空气的计算域取1.2 m×0.8 m×0.8 m,混凝土板的网格总数为240 000,空气和TNT炸药的网格数为768 000。
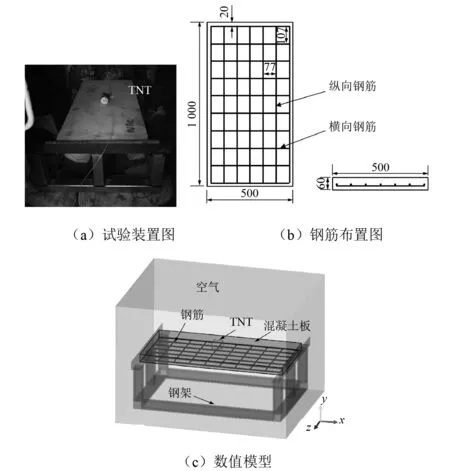
图3 钢筋混凝土板爆炸试验布置图Fig.3 Explosion test of reinforced concrete slab
图4给出了数值模拟结果与现场实测结果的对比。由图4可以看出,空中接触爆炸荷载作用下钢筋混凝土板呈现典型的冲切破坏模式。数值计算的混凝土板正面破碎区直径和背面剥落区直径分别为20 cm和29 cm,与试验结果的18 cm和32 cm非常接近。数值计算的混凝土板正面和背面的损伤分布与现场试验结果均吻合较好,说明采用的耦合计算方法及材料模型可以较好地描述爆炸冲击荷载作用下钢筋混凝土结构的动力响应特性。

图4 数值计算结果与现场试验结果对比图Fig.4 Comparison of the numerical and experimental results
3 爆炸荷载作用下隧道的动力特性分析
3.1 水底隧道全耦合数值模型
选取某水底隧道典型的断面为研究对象,该段隧道宽33.8 m,高8.4 m,顶部最大水深8.0 m。顶板厚1.1 m,侧墙厚0.85 m,中墙厚0.6 m,底板厚1.2 m,如图5所示。单向通道宽13.9 m,中间布置3.2 m宽的维修及安全通道。数值模型的长度选择为20 m,如图5(b)所示。混凝土材料的抗压强度和抗剪模量分别为40 MPa和16.7 GPa,其他材料参数见表1。钢筋布置采用双向双层的方式,钢筋直径为28 mm,间距为200 mm,如图5(c)所示。钢筋的弹性模量和屈服强度分别为200 GPa和400 MPa。

图5 水底隧道模型布置图(m)Fig.5 Geometry of the underwater tunnel (m)
该数值模型由空气、水、钢筋混凝土隧道、地基和TNT炸药组成。为了简化数值模型,地基采用线弹性材料模拟(弹性模量为20 GPa,泊松比为0.25)。由于爆炸荷载主要作用在隧道的顶板,隧道周围饱和土对其动力响应影响较小;同时,饱和土的力学性质与流体非常相似,因此将隧道两侧的饱和土体简化成水体。
采用Lagrange方法模拟隧道和地基,采用Euler网格对空气、水和TNT炸药进行模拟,采用Beam单元对钢筋进行网格划分。混凝土材料及钢筋的网格大小均为150 mm,假设钢筋与混凝土连接良好且无相对滑移。在炸药中心位置,网格大小约为100 mm,随着距爆源距离的增大,网格尺寸逐渐增大。该数值模型由425 200个Lagrange单元和1 296 000个Euler单元组成。在Euler计算域的外围施加无反射边界,以减小冲击波在计算边界处的反射;在地基的底面及侧面施加透射边界,允许应力波自由传播;在地基的底面施加固定约束。
对于起爆距离较近的情况,炸药爆炸后猛烈的冲击荷载直接作用于结构迎爆面,导致隧道顶部可能出现压缩、冲切及剥落等破坏,结构以局部破坏为主。相对于几十甚至上百兆帕的冲击荷载,静荷载对其局部破坏模式影响有限。对于整体破坏模式,结构以整体弯曲破坏为主,通过对比分析发现,初始静荷载对爆炸荷载作用下隧道结构的破坏模式影响有限,但考虑初始静荷载后,隧道的整体变形略有增大。为了提高计算效率,本文暂时未考虑静力荷载的作用。
3.2 爆炸荷载作用下水底隧道的毁伤特性
图6为水下爆炸荷载作用下隧道的毁伤发展过程,炸药当量为40 kg,起爆距离为2.0 m。炸药起爆之后,近似球形的冲击波向外发散传播;在t=3.5 ms左右,隧道顶板内的应力波传至顶板背面,产生的反射拉应力超过了混凝土的动态抗拉强度,隧道顶板背面出现了剥落破坏(见图6(a));在t=7 ms时,隧道顶板的剥落损伤进一步发展;由于爆炸压力在水中的衰减速度比在空气中要慢,因此隧道顶面会承受更大的分布荷载,导致隧道顶部出现整体弯曲变形。在t=15 ms时,由于顶板整体弯曲变形导致顶板与边墙和中墙的交界处出现受拉损伤,如图6(c)所示;随着时间的推移,拉伸损伤区进一步发展,如图6(d)所示;在t=50 ms时,隧道的毁伤发展基本停止。如图6(e)、图6(f)所示,隧道顶板与边墙及中墙交界处的裂缝发育完全,跨中沿轴线方向也出现了严重的弯曲破坏。

图6 水下爆炸荷载作用下隧道毁伤发展过程 (40 kg, 2.0 m)Fig.6 Damage evolution of underwater tunnel subjected to blast loads (40 kg, 2.0 m)
图7为作用于隧道顶面的压力峰值分布图。可以看出,当起爆距离为2.0 m时,作用在隧道上的爆炸荷载分布极不均匀;作用在隧道的爆炸荷载峰值压力超过了70 MPa。由于应变率和流固耦合效应的影响,隧道顶面没有出现明显的压碎区,但隧道顶板背面出现了严重的剥落破坏(见图6(f))。同时可以发现,远离爆源的隧道顶面压力峰值也达到了5 MPa。因此,当炸药当量为40 kg、起爆距离为2.0 m时,隧道结构呈现整体的弯曲破坏和局部的剥落破坏。
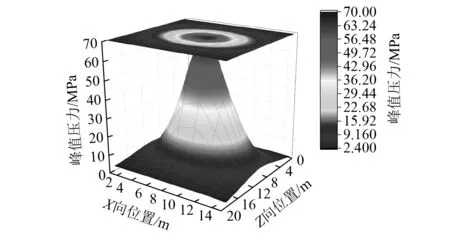
图7 隧道顶面压力峰值分布图 (40 kg, 2.0 m)Fig.7 Distribution of peak pressure (40 kg, 2.0 m)
4 爆炸荷载作用下水底隧道的破坏模式
4.1 起爆距离对水底隧道破坏特征的影响
由上述分析可知,当炸药TNT当量为40 kg、起爆距离为2.0 m时,水底隧道的破坏模式为整体弯曲破坏伴随着正对爆源的局部剥落破坏。进一步分析了当起爆距离较小(起爆距离小于2.0 m)或者较大(起爆距离大于2.0 m)的情况下,隧道结构的毁伤模式。
图8给出了起爆距离为1.0 m、炸药当量为5 kg时,隧道的毁伤发展过程。对于近距离水下爆炸荷载,当炸药当量较小时,仅在炸药正下方的混凝土产生剥落破坏,结构整体变形较小。但隧道顶板的剥落破坏会产生高速的破片,可能会造成隧道内部的人员伤亡。一旦开裂区域贯通,外部的水体将倒灌入隧道,虽然没有发生整体的坍塌,但是贯穿的通道不易修补,且透水对隧道内的车辆及人员安全也将构成巨大威胁。

图8 水下爆炸荷载作用下隧道毁伤发展过程 (5 kg, 1.0 m)Fig.8 Damage evolution of underwater tunnel subjected to blast loads (5 kg, 1.0 m)
对于接触或小距离爆炸情况,水底隧道的局部破坏机制如图9所示。炸药起爆之后,爆炸冲击波首先压缩最近的混凝土材料,当混凝土内应力超过其动态抗压强度时,隧道顶部将出现压碎区;传入顶板的压缩波遇到临空面后将反射生成拉伸波,若反射拉应力超过混凝土的动抗拉强度,顶板背面将产生剥落破坏。除了爆炸冲击波的作用之外,爆轰产物将与结构面相互作用,由于壁面反射及流固耦合相互作用,在水体与隧道顶面交界处还将发生空化现象。
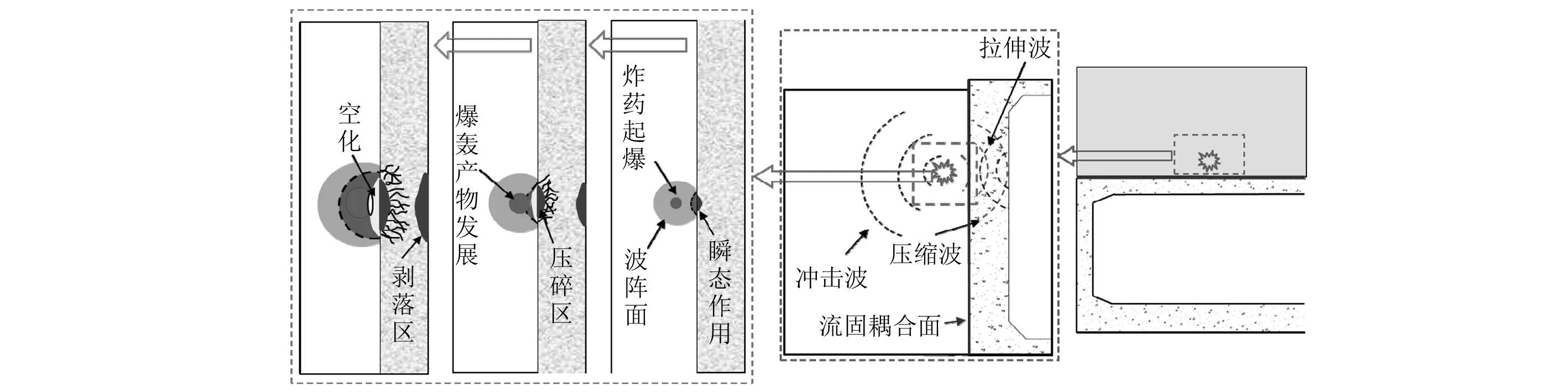
图9 接触或近场爆炸荷载作用下隧道结构的局部毁伤机制Fig.9 Local damage mechanism of the tunnel under contact or close-in blast loads
图10为40 kg当量TNT、爆炸距离为4.0 m时,隧道结构的毁伤发展过程。在t=10 ms时,由于拉应力的作用,顶板背面出现了轻微的损伤(见图10(a));随着时间的推移,在顶板跨中出现了拉破坏;同时,顶板与墙体交界处的混凝土产生了拉损伤,如图10(b)所示。图10(e)和图10(f)为隧道的最终破坏形态,由于顶板产生向下弯曲变形,导致三个不同位置出现破坏,分别为顶板与边墙交界处、顶板与中墙交界处以及顶板跨中。可以看出,当起爆距离增加到4.0 m时,隧道呈现整体弯曲的破坏模式,但未发生明显的局部剥落破坏。

图10 水下爆炸荷载作用下隧道毁伤发展过程 (40 kg, 4.0 m)Fig.10 Damage evolution of the underwater tunnel subjected to blast loads (40 kg, 4.0 m)
图11为不同起爆距离下隧道顶板的变形对比图,炸药当量为40 kg,起爆距离分别为2.0 m和4.0 m。两种起爆距离下的变形分布规律非常相似;随着起爆距离的增大,顶板的响应逐渐减小;当距离从2.0 m增大至4.0 m时,隧道顶板最大位移由240 mm降至155 mm。原因之一是随着爆炸距离的增加,作用在顶部的压力载荷变小;另一个原因是更多的爆炸能量将从自由水面消散。同时可以发现,随着起爆距离的增大,隧道顶板的位移沿轴向变化更加平缓,也说明了随着起爆距离的增大,结构逐渐趋向于整体变形。
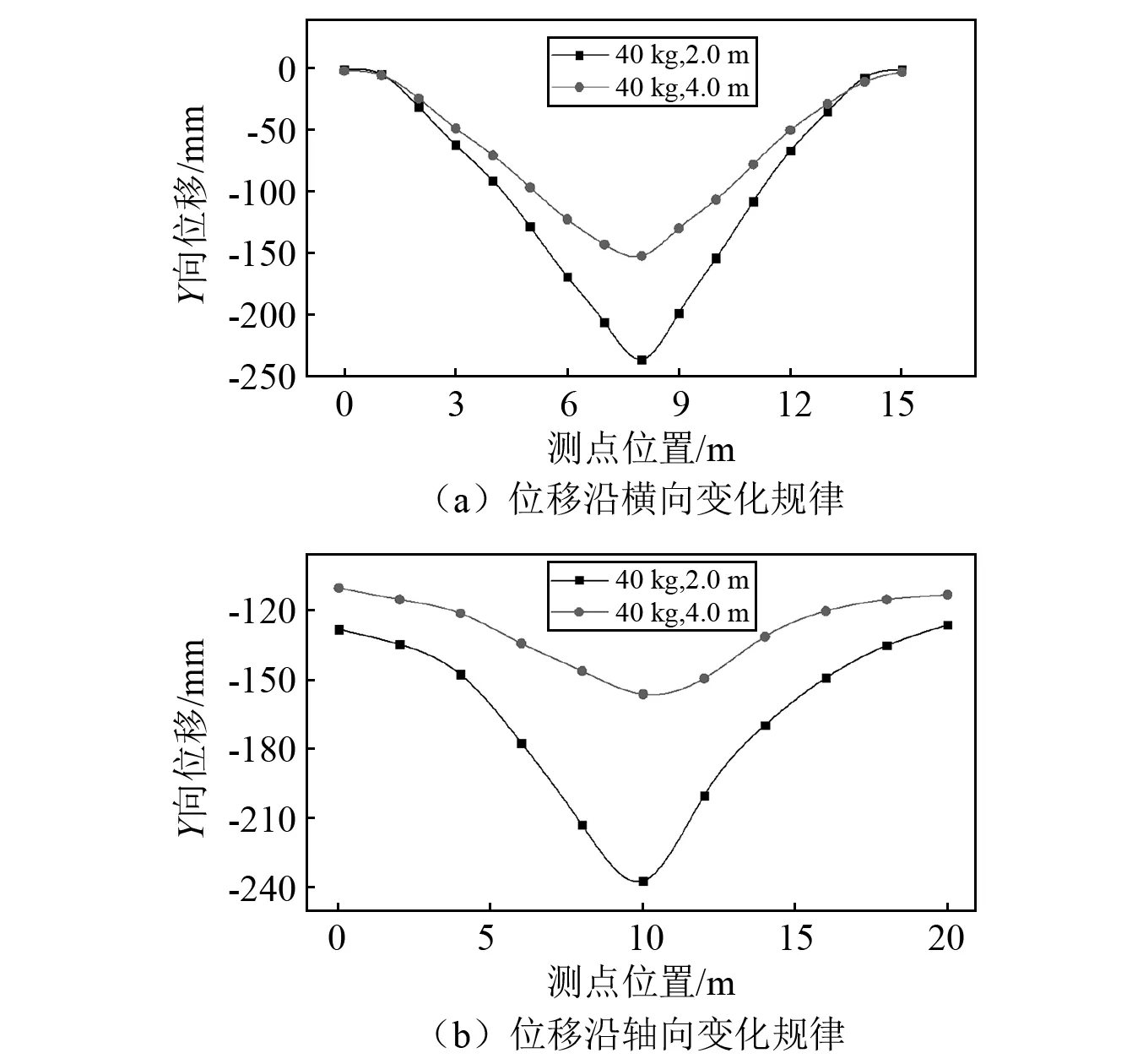
图11 不同起爆距离条件下隧道顶板的变形图Fig.11 Deformations of the tunnel with different explosion distances
图12为起爆距离较大时,水底隧道的整体毁伤机制。对于起爆距离较大情况下,传至隧道顶面的冲击波强度较小,因此顶板的压碎区可能较小;但由于混凝土的抗拉强度很低,顶板背面可能会出现剥落损伤;同时,作用在隧道顶板的分布荷载较大,导致顶板发生整体的弯曲破坏,顶板与边墙及中墙的交界处可能出现拉裂。
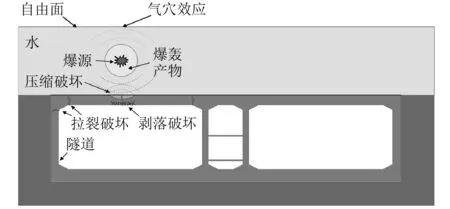
图12 水下爆炸荷载作用下隧道的整体毁伤机制Fig.12 The global damage mechanism of the tunnel subjected to underwater explosions
4.2 水下爆炸荷载作用下水底隧道的破坏模式
上述分析结果表明:不同起爆距离下水底隧道的破坏模式是完全不同的。起爆距离较小时,隧道呈现局部破坏模式,整体变形较小;当起爆距离较大时,隧道呈现整体弯曲的破坏模式。为了进一步探讨不同水下爆炸荷载作用下隧道的毁伤模式,研究了不同起爆距离、不同炸药当量作用下水底隧道的毁伤分布特征。
图13给出了该水底隧道在不同水下爆炸荷载作用下典型的破坏形态。根据该隧道的破坏特征,可将其破坏模式分为三类:①局部冲切(剥落)破坏;②整体弯曲破坏伴随着局部剥落破坏;③整体弯曲破坏。如图13(a)所示,当起爆距离小于2.0 m时,该水底隧道呈现局部冲孔或剥落破坏模式,整体变形可以忽略不计;当起爆距离为2.0~4.0 m,隧道呈现整体弯曲破坏,伴随着局部剥落(冲切)破坏,如图13(b)、图13(c)所示;当起爆距离超过4.0 m,隧道以整体弯曲破坏为主,其毁伤分布如图13(d)、图13(e)所示。

图13 水下爆炸荷载作用下水底隧道的毁伤模式Fig.13 Failure patterns of the underwater tunnel subjected to blast loads
5 结 论
基于Lagrange-Euler全耦合方法建立了水底隧道水下爆炸全耦合模型,研究了水下爆炸荷载作用下隧道的损伤发展过程及其损伤分布特征,给出了水下爆炸冲击荷载作用下水底隧道的毁伤机理及毁伤模式。主要得到以下结论:
(1)数值模拟的混凝土板损伤分布特征与试验结果吻合较好,说明采用的Lagrange-Euler耦合计算方法及材料模型能够有效地预测爆炸荷载作用下混凝土结构的动力响应。
(2)水下爆炸冲击荷载作用下水底隧道的毁伤机制主要包括顶板迎爆面的爆炸压缩破坏、顶板背面的反射拉伸破坏以及整体弯曲破坏等。
(3)水下爆炸荷载作用下该水底隧道的破坏模式可以分为三类:当起爆距离小于2.0 m时,隧道呈现局部冲孔或剥落破坏模式;当起爆距离为2.0~4.0 m,隧道呈现整体弯曲破坏,伴随着局部剥落(冲切)破坏;当起爆距离超过4.0 m,隧道表现为整体弯曲破坏。

