PSO优化多尺度一维卷积神经网络的风机基础螺栓松动诊断

徐培文, 陈仁祥 ,胡小林, 杨黎霞, 唐林林, 林 立

(1.重庆交通大学 交通工程应用机器人重庆市工程实验室, 重庆 400074；2.重庆工业大数据创新中心有限公司， 重庆 400056)

风机是工程中应用广泛的通风装置，工程现场中，其恶劣的工作环境以及长时间的运行状态下，容易致使风机安装基础螺栓松动，影响风机正常工作和通风安全，特别针对悬挂风机，一旦掉落将造成严重后果，因此，对风机基础螺栓进行有效地松动诊断具有重要意义[1]。

目前，通过振动信号实现风机基础螺栓松动诊断是较为有效的方法[2]，振动传感器的安装、振动信号的采集较为方便，且对风机结构无损伤，对环境要求不高。而面向庞大的振动信号数据，如何从数据中挖掘出有效的风机基础螺栓松动特征是通过振动信号实现风机基础螺栓松动诊断的关键。

卷积神经网络(convolution neural network ,CNN)作为经典的深度学习模型，其局部感知、权值共享和下采样技术可有效降低网络复杂度，具有强鲁棒性和容错能力，在目标检测、故障诊断等众多领域得到了广泛应用[3-4]。鄢仁武等[5]以小波时频图输入卷积神经网络，实现短路器故障诊断。Wen等[6]通过将时域信号转化为二维图像并结合CNN实现轴承和离心泵的故障诊断。卷积神经网络处理的信号一般是二维图像信号，而针对一维信号，采用一维卷积神经网络更具优势[7]。曲建岭等[8]通过一维卷积神经网络实现滚动轴承故障诊断；吴春志等[9]应用一维卷积神经网络实现齿轮箱故障诊断。以上通过一维卷积神经网络进行机械设备故障诊断取得了不错的效果，然而网络中不同尺度卷积核具备不同的感受野，当风机转速等工况改变时振动特征发生改变，势必需要不同的感受野来学习特征，需要运用多个不同尺度卷积核进行特征提取从而有效增强网络的特征表达能力[10]。

郭晨等[11]运用深度多尺度一维卷积神经网络实现雷达舰船目标识别；吴俊等[12]通过多尺度一维卷积神经网络实现光纤振动事件识别。以上方法通过多尺度一维卷积神经网络进行复杂的目标识别，取得了不错的效果，但实际工程中，风机特点与转速的变化增加了数据的复杂度，如何选取合适的卷积核数目和尺度以自适应提取数据特征具有重要意义。卷积核数目增多，尺度增大，导致网络训练参数增加，增加了网络复杂度，影响训练效率；相反，卷积核数目和尺度过小，导致特征提取不充分，影响网络识别效果。因此，对卷积核数目和尺度进行自动寻优是提升网络特征提取能力和识别效果的关键。目前，粒子群优化(particle swarm optimization, PSO)利用群体中的个体对信息的共享从而使得整个群体的运动在问题求解空间中产生从无序到有序的过程，进而获得问题最优解，在寻求二维卷积神经网络最优参数上得到应用[13]，为面向风机基础螺栓松动诊断的多尺度一维卷积神经网络卷积核数目和尺度优化问题提供了启发。

综合以上分析，提出PSO优化多尺度一维卷积神经网络的风机基础螺栓松动诊断方法。以多尺度一维卷积神经网络中的卷积核数目和尺度作为粒子群算法的粒子，将验证精度最大的粒子适应度值作为卷积核数目和尺度参数确定依据，通过粒子速度和位置的不断更新，获取最优卷积核数目和尺度参数，得到最优参数下的多尺度一维卷积神经网络，实现风机基础螺栓松动诊断。稳定转速和升降速下试验证明，所提方法可在非经验指导下获取最优卷积核数目和尺度，降低了人为选取合适的卷积核数目和尺度的经验要求，优化后的多尺度一维卷积神经网络可从一维原始信号中提取出有效松动特征，具备良好的诊断效果。

1 PSO优化多尺度一维卷积神经网络

1.1 多尺度一维卷积神经网络

多尺度一维卷积神经网络包含多尺度卷积层、池化层、全连接层等基本结构，如图1所示。考虑不同尺度卷积核具备不同的感受野，多尺度卷积层中采用并行多个不同尺度卷积核对输入信号进行不同尺度的卷积，从不同特征感受野层面对输入信号特征充分表达，多尺度卷积层和池化层交替出现，将最后池化层的特征映射图首尾连接形成特征向量，特征向量通过全连接得到分类向量，最后由Softmax多分类器完成分类。

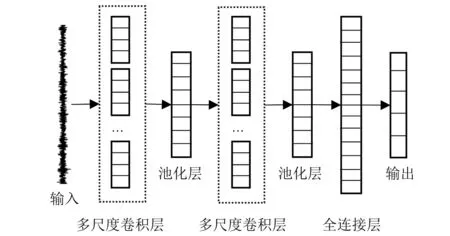
图1 多尺度一维卷积神经网络结构Fig.1 Multi-scale one-dimensional convolutional neural network structure

1.1.1 多尺度卷积层

多尺度卷积层中通过多个不同尺度的卷积核对输入信号进行不同尺度的卷积，其卷积定义为

(1)

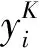
f(x)=max(0,x)

(2)

1.1.2 池化层

池化层是对上一层数据的缩放映射，通过池化对输入数据进行子采样，可大幅减少输入数据的空间维度，池化运算如式(3)所示

yi=f[βidown(x)+bi]

(3)

式中:down(*)为下采样函数;βi为第i个特征的权值；x对应上一层(卷积层)的输出；bi为第i个特征的偏置。

1.1.3 全连接层和Softmax多分类器

全连接层包含对应多层感知机的隐含层，该层中所有神经元与前一层中神经元全连接，可以整合卷积层、池化层中具有类别区分性的局部信息。全连接层后接一个隐藏层，最后由Softmax多分类器完成分类。假设由k类的分类问题，Softmax多分类器的输出可以计算为

(4)

式中：W和b分别为权重矩阵和偏置值；O为卷积神经网络的最终输出。

1.2 PSO优化多尺度一维卷积神经网络

粒子群算法是一种群体演化算法，可以通过群体和个体之间的行为交互实现种群进化。首先随机初始化一群粒子，并根据法则更新其速度和位置，最终找到最优解。PSO主要通过追踪个体和整体的最佳值(pbest,gbest)来更新粒子的速度和位置，个体和整体的最优值通过适应度值评价，适应度值是对PSO搜索的解的品质的评价指标，通过计算每个粒子的适应度值，进而获取粒子个体和整体的最优值。

速度和位置更新法则如式(5)、式(6)所示。

vi=ωvi+c1r1(pbesti-xi)+c2r2(gbesti-xi)

(5)

xi=xi+vi

(6)

式中:vi为粒子的速度；ω为惯性因子，其值为非负；c1为个体学习因子；c2为整体学习因子；r1,r2为(0,1)范围内的随机数；xi为粒子的当前位置。

PSO优化多尺度一维卷积神经网络流程，如图2所示,具体步骤如下：

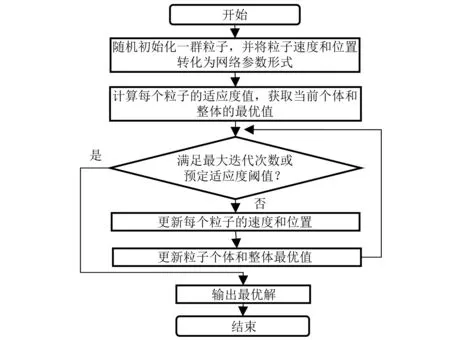
图2 优化流程Fig.2 The optimization process

步骤1将多尺度一维卷积神经网络参数作为PSO的粒子，把粒子速度和位置转化成由网络参数构成的向量形式，其位置表示当前粒子对应的网络参数，速度表示粒子位置更新(网络参数更新)的大小和方向，随机初始化一群粒子。

步骤2以验证精度作为适应度值，评估每个粒子的适应度值并得到当前个体和整体最优值，个体最优值为每个粒子在搜索空间中单独搜寻的最优值，整体最优值为所有粒子在搜索空间搜索的最优值。

步骤3根据式(5)、式(6)，通过追踪个体和整体的最优值以更新粒子的速度和位置。

步骤4评估更新后的粒子适应度值，若粒子适应度值优于当前整体最优值，就把整体最优值设成当前位置。

步骤5重复步骤3、步骤4，直到达到最大迭代次数或满足预定适应度阈值，停止搜索，输出整体最优值，即为最优多尺度一维卷积神经网络参数。

2 PSO优化多尺度一维卷积神经网络的风机基础螺栓松动诊断流程

PSO优化多尺度一维卷积神经网络的风机基础螺栓松动诊断方法通过PSO优化算法获取多尺度一维卷积神经网络卷积核数目和尺度最优参数，以更好地适应原始信号特征提取(特别是变转速条件下)，再通过优化后最优参数下的多尺度一维卷积神经网络实现风机基础螺栓松动诊断。其流程如图3所示。

图3 方法流程图Fig.3 The method flow chart

具体步骤如下：

步骤1获取风机一维原始振动信号，划分训练集、验证集与测试集。

步骤2构建多尺度一维CNN网络结构，将多尺度卷积层中卷积核数目(使用的不同尺度卷积核数目)和尺度(对应该数目下的不同卷积核尺度大小)作为PSO的粒子进行网络训练及验证。

步骤3以验证集上验证精度最大的粒子适应度值作为卷积核数目和尺度确定依据，根据适应度值不断更新粒子速度与位置。

步骤5达到最大迭代次数或满足预定适应度(验证精度)阈值，获取最优卷积核数目和尺度参数，得到最优参数下的多尺度一维卷积神经网络。

步骤6输入测试集，得到诊断结果。

3 试验结果与分析

3.1 试验数据与参数设置

通过某悬挂风机预埋基础螺栓松动诊断问题进行试验。该风机安装结构和测试示意图，如图4所示，安装时首先在隧道拱顶预埋钢筋，预埋钢筋与预埋钢板通过螺栓连接，预埋钢板上焊接U形块，U形块连接风机安装支架将风机固定在隧道顶上。预埋钢板上共有10颗连接螺栓，每颗连接螺栓都存在预紧和松动两种状态。试验布置12个测点，1～10号测点布置在1～10号螺栓旁边，测点11、测点12分别布置在两块安装支架上。由于风机基础螺栓分布对称，并考虑实际工程中螺栓松动情况，试验模拟了5种典型的连接螺栓松动状态，分别为螺栓全紧、1～4颗螺栓松动状态(螺栓1松动、螺栓2、螺栓4松动、螺栓1、螺栓3、螺栓5松动、螺栓1、螺栓2、螺栓3、螺栓6松动)，若螺栓松动数量达到4颗以上，则风机运行十分危险，必须停机维护。采用PCB加速度传感器、NI9234采集卡采集振动信号，根据采样定理，并保证所采集信号完整地保留原始信号中的信息，采样频率设置为25.6 kHz，采样长度为100 K。

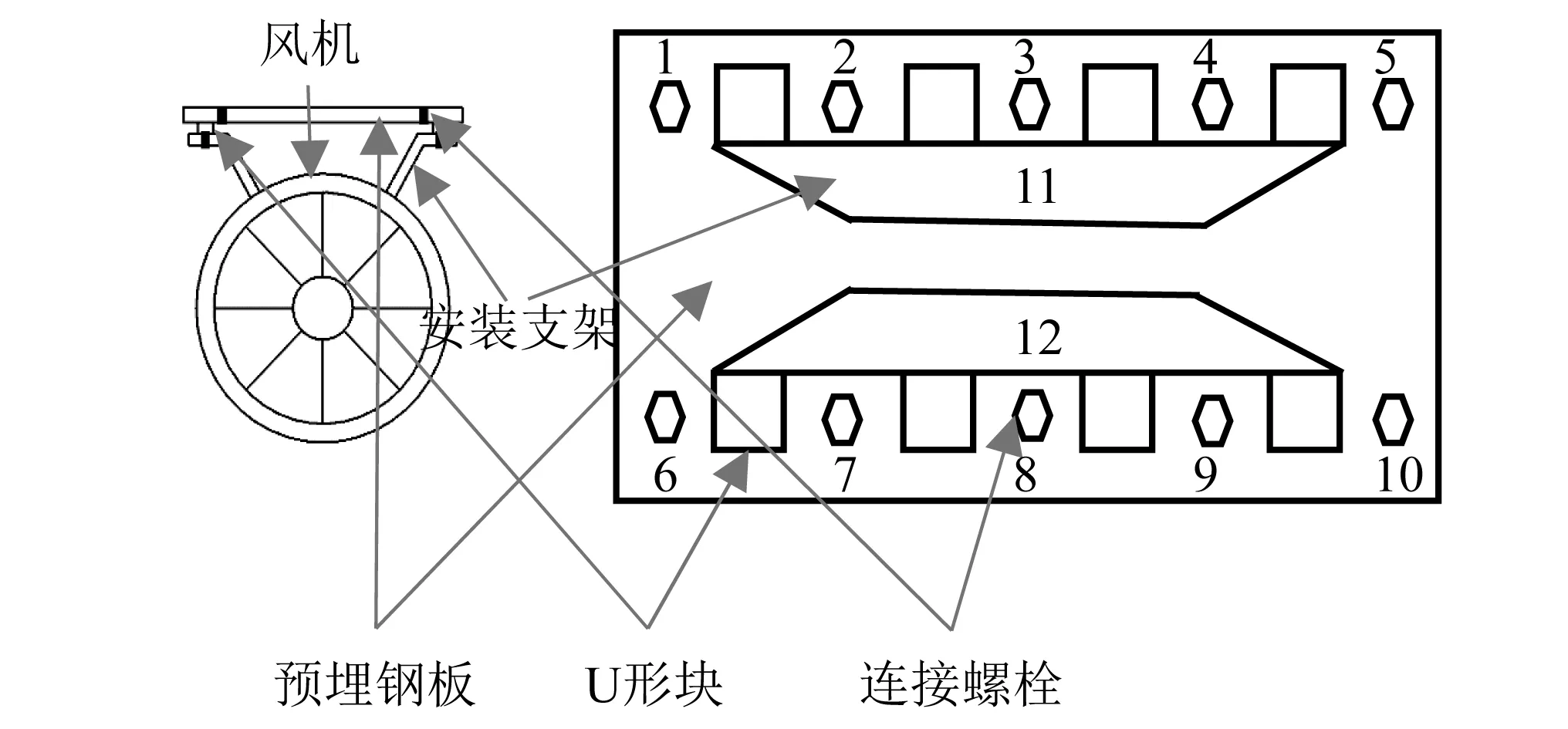
图4 风机安装和测试示意图Fig.4 Installation and test diagram

在稳定转速下对5种风机基础螺栓松动状态，每种状态随机取200个样本构建样本集，每个样本长度为1 024点，以6∶1∶3的比例划分训练集、验证集及测试集，即训练集、验证集和测试集样本数分别为600,100,300。多尺度一维卷积神经网络由两层多尺度卷积层、两层池化层和全连接层组成，池化方式为最大值池化，采用交叉熵作为损失函数，优化器选用AdadeltaOptimizer自适应调整学习率，批量大小为100，迭代次数为100。PSO中粒子数量为40，迭代次数为10，学习因子c1=c2=2，惯性因子ω=0.1。计算环境为：python+keras，Inter i7-8750H+Nvidia 1050ti。

3.2 不同卷积核数目和尺度分析

为分析不同卷积核数目和尺度对网络性能的影响，在第一层卷积层中采用不同的卷积核数目和尺度进行了对比分析。图5(a)为不同卷积核尺度下诊断精度对比曲线，根据该图，不同卷积核尺度下，诊断精度存在差异，其原因是不同卷积核尺度具备不同的感受野，对信号特征表达不一，因而对诊断结果影响较大。图5(b)为不同卷积核数目下诊断结果对比，其中对应不同数目下的卷积核尺度根据图5(a)中诊断效果较好的几种卷积核尺度进行设置，其中S(2,8)表示使用的2种不同卷积核尺度分别2、8,T(38.4 s)表示其训练时间为38.4 s。由图5(b)可知，当采用3种不同尺度卷积核时，诊断效果表现最优；增加卷积核数目，其训练时间明显增加，且诊断精度存在下降趋势，其原因是数目增加导致网络训练参数增加，并导致数据信息过提取，诊断效果变差。因此，综合诊断精度和计算效率，在PSO中对于卷积核数目的解空间范围设置在[2，3]，并结合样本长度，为涵盖从小到大感受野范围内的卷积核尺度，卷积核尺度解空间范围设置为[1,32]。

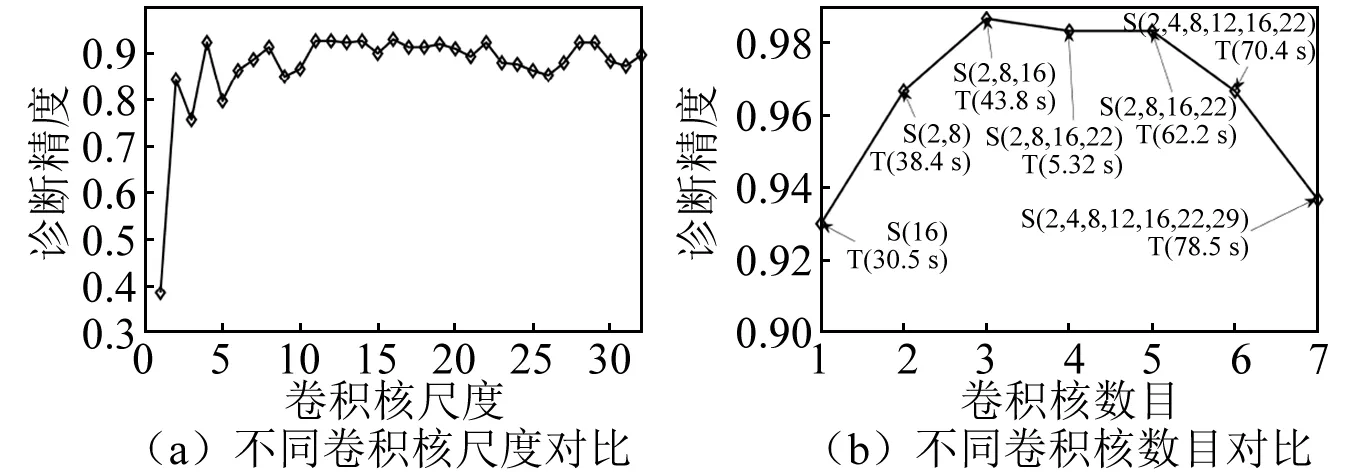
图5 不同卷积核数目和尺度对比Fig.5 Comparison of the number and scale of different convolution

3.3 优化过程分析

为展现粒子群优化算法优化过程，并验证PSO优化多尺度一维卷积神经网络的可行性，在PSO每次迭代更新粒子速度和位置后计算整体最优值下的适应度值，得到适应度曲线，如图6所示。根据该图，随着每次迭代更新粒子速度和位置后，适应度值不断提高，说明粒子速度和位置不断更新过程搜索到的解的品质不断提高，实现了整个粒子群体的进化；在迭代6次后适应度值稳定，最终得到适应度值最优解，相应的整体最优值即为卷积核数目和尺度最优参数。

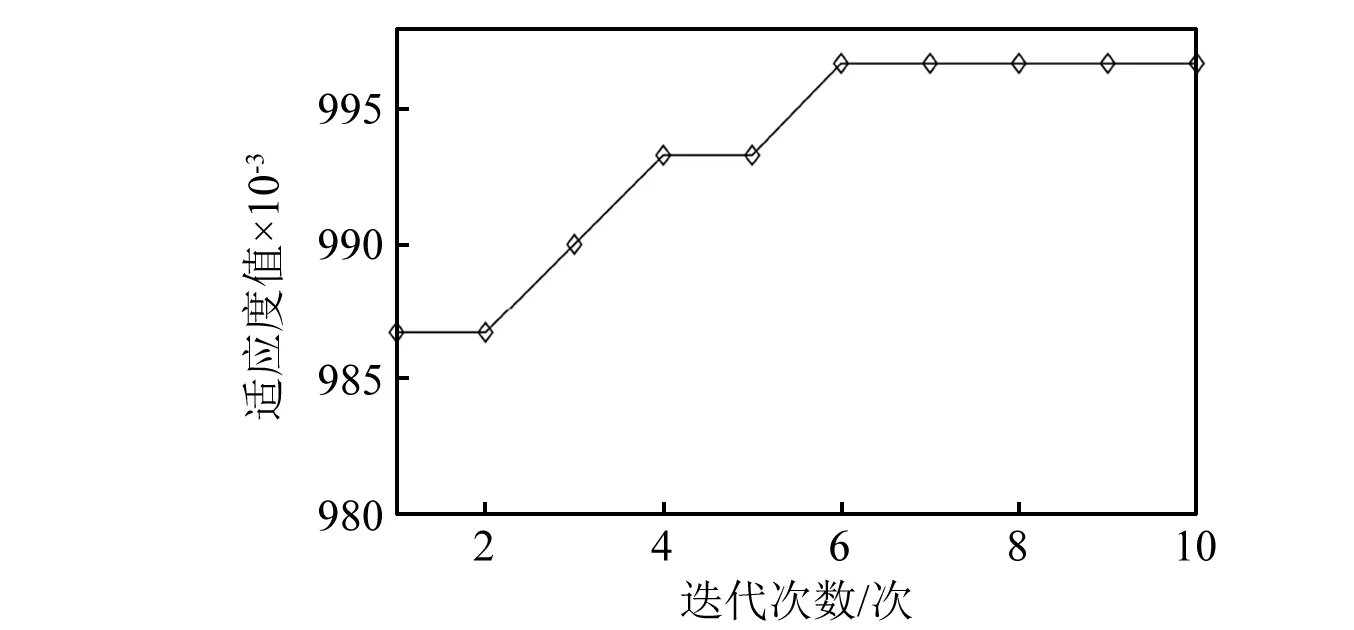
图6 不同迭代次数下适应度曲线Fig.6 Fitness curve under different iteration times

3.4 稳定转速下基础螺栓松动诊断

3.4.1 试验结果及分析

为评估所提方法在稳定转速下对风机基础螺栓松动诊断效果，并验证PSO优化后确定的多尺度一维卷积神经网络参数的有效性(两层多尺度卷积层采用的不同尺度卷积核数目均为3，第一层中尺度6、10、29被采用，第二层中尺度24、26、31被采用)。根据卷积核数目和尺度解空间设置，试验考虑两层多尺度卷积层中不同尺度卷积核数目所有组合情况，对应两层多尺度卷积层，其卷积核数目组合情况分别为(2、2，2、3，3、2，3、3)，并结合图5(a)不同卷积核尺度下的诊断结果以及郭晨等和吴俊等研究中对多尺度卷积层的参数设置。人为试验设置出诊断效果较好的几组参数组合，选取的参数组如表1所示，N2-S2,8中N2表示卷积核数目为2，S2,8表示卷积核尺度分别为2，8。同时对比使用单一尺度的一维卷积神经网络(one-dimensional convolutional neural network，1DCNN)[9]。

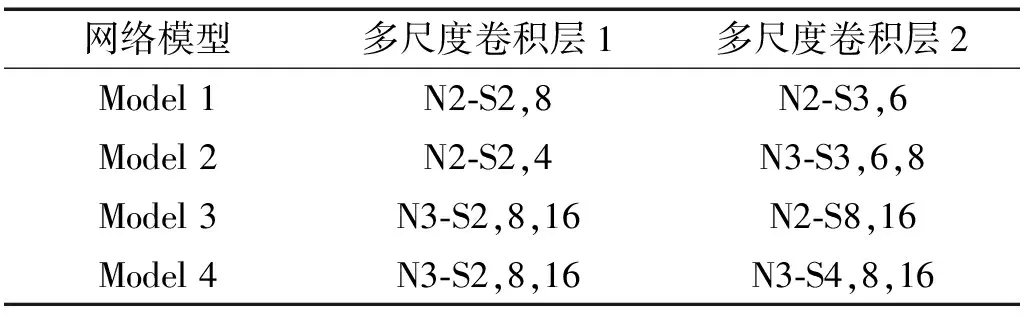
表1 对比网络参数组合情况

各方法经100次迭代，每次迭代更新权重后输入测试集进行测试，得到不同迭代次数下测试精度对比曲线(曲线通过smooth函数拟合)，如图7所示。由该图，随着迭代次数的增加，各方法测试准确率不断提高，所提方法和使用多尺度卷积核的Model1、Model2、Model3、Model4的最终准确率均高于1DCNN，证明了使用多尺度卷积核进行特征提取可有效增强网络的特征表达能力，具备更好的诊断效果；对比各多尺度一维卷积神经网络，不同卷积核数目和尺度参数下，其诊断结果均存在差异，所提方法在测试准确率上均优于其他人为试验确定参数的多尺度一维卷积神经网络，且在迭代50次时准确率便达到0.994，其他方法明显较低。同时，所提方法随迭代次数的增加，准确率波动平稳，其余多尺度一维卷积神经网络准确率上升缓慢且准确率波动较为明显。证明了PSO优化多尺度一维卷积神经网络在非经验指导下获取最优参数可有效适应原始信号特征提取，提升网络性能，具备更好的诊断效果，并具备良好的稳定性。

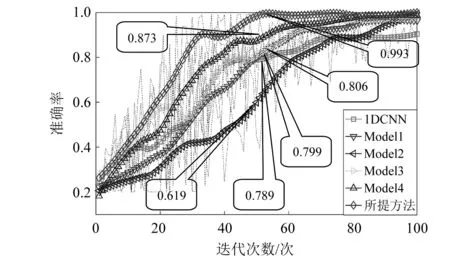
图7 稳定转速下准确率对比Fig.7 Comparison of the accuracy under steady speed

每个网络模型随机抽取样本经10次测试后取平均，得到平均诊断准确率，并计算其标准差，同时对比分析各网络模型训练耗时，结果如表2所示。由表2可知，人为试验确定参数的Model2、Model3、Model4平均准确率均达到0.97以上，也具备较好的诊断效果，然而人为试验确定参数过程繁琐，耗时费力且依赖经验指导；所提方法在训练耗时上稍高于其他网络模型，其耗时取决于模型的空间复杂度以及卷积核尺度大小带来计算参数量的不同，但避免了人为试验确定参数过程，人为试验确定参数过程耗时无法统计，且无法保证所确定参数的有效性；所提方法可在非经验指导下获取网络最优参数，平均诊断准确率达0.994，优于其他方法，且标准差更小。证明了所提方法可有效实现风机基础螺栓松动诊断，且偏差小，稳定性好。

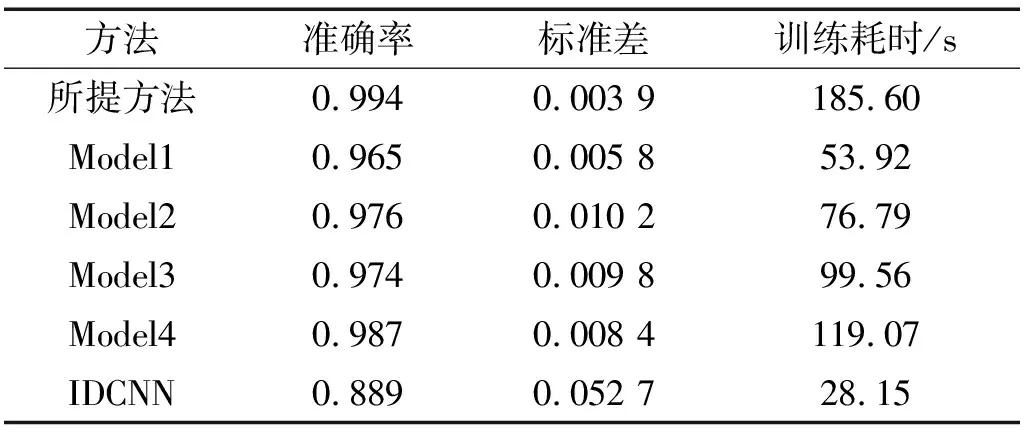
表2 稳定转速下诊断结果对比

3.4.2 特征学习验证

为验证PSO优化算法确定最优卷积核数目和尺度参数后的多尺度一维卷积神经网络对原始数据的特征学习能力，利用t分布随机邻域嵌入(t-distributed stochastic neighbor embedding, t-SNE)对全连接层前(即特征输出层后)所提特征进行可视化分析，同时与各多尺度一维卷积神经网络和1DCNN对比，可视化分析结果如图8所示。由图8可知，所提方法提取的同一种松动状态的特征聚集性最好，不同松动状态的特征能有效地分离，所提特征具备良好的区分性，其特征提取能力优于其余方法，其余算法所提特征均存在部分混叠(Model4提取特征的区分性也较好，根据表2，该模型准确率仅次于所提方法)，验证了所提方法可有效适应原始信号特征提取，能从一维原始信号中提取出风机基础螺栓松动特征，可有效表征风机基础螺栓松动状态。

图8 学习特征t-SNE分析Fig.8 t-SNE analysis of learning features

3.5 升降速下基础螺栓松动诊断

考虑实际工程中不同风机具有不同的运行转速，通过风机升速(500～1 500 r/min)和降速(1 500～500 r/min)运行时采集振动信号以适应对不同转速风机基础螺栓松动诊断，每次采样时间为4 s,升降速时加速度为4.2 r/s2。针对5种风机基础螺栓松动状态，每种状态取样本数为200(包含升速、降速各100个样本)，每个样本长度为1 024，同样以6∶1∶3的比例划分训练集、验证集及测试集，即训练集、验证集和测试集样本数分别为600,100,300。经PSO优化后的多尺度一维卷积神经网络中两层多尺度卷积层采用的不同尺度卷积核数目均为3，第一层中尺度8,11,22被采用，第二层中尺度7,9,25被采用。

3.5.1 试验结果及分析

经100次迭代，每次迭代更新权重后输入测试集进行测试，得到升降速下不同方法准确率对比曲线，如图9所示。根据该图，所提方法在升降速数据下测试精度同样优于其余对比方法，且随迭代次数增加，准确率波动更为平稳，具备更好的稳定性。

图9 升降速下准确率对比Fig.9 Comparison of the accuracy under rising and falling speed

各方法随机抽取样本经10次测试后取平均，得到升降速下不同方法诊断结果对比，如表3所示。由表3可知，相对稳定转速下诊断结果，各方法诊断准确率均存在一定下降趋势，其原因是升降速下，原始数据中存在转速干扰，增加了对松动特征提取的难度；所提方法在训练耗时上仍稍高于其余网络模型，但诊断准确率达0.974，明显优于其余方法。其余方法诊断准确率相对于稳定转速下的诊断结果均下降明显，其原因是数据复杂程度不一，当前网络参数无法有效适应数据特征提取，验证了所提方法通过PSO优化算法确定网络参数后可有效增强网络特征提取能力，从数据中提取有效松动特征，具备良好诊断效果。

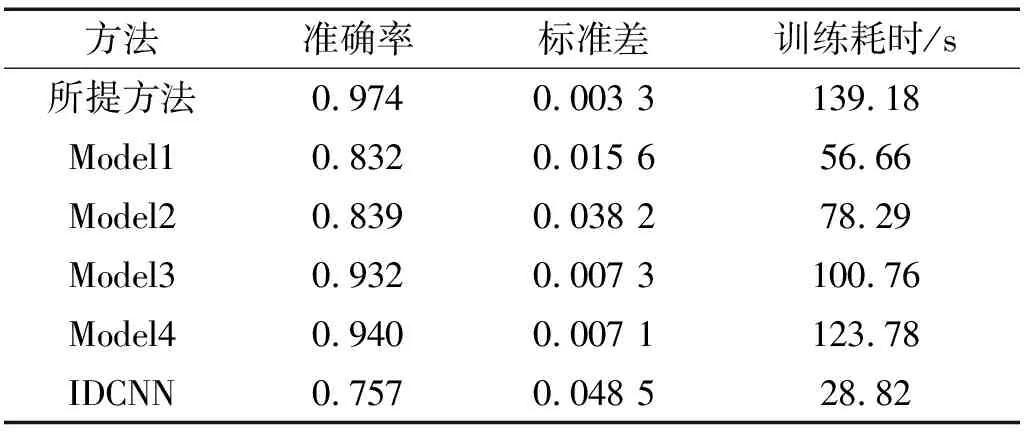
表3 升降速下诊断结果对比

3.5.2 特征学习验证

为证明升降速下所提方法的特征提取能力，利用t-SNE对各方法所提特征进行分析和可视化，如图10所示。综合图8和图10，所提方法在稳定转速和升降速下提取的特征具有良好的聚类特性和区分性，证明了所提方法能有效获得最优参数，确保诊断的准确率。而其他方法在升降速条件下不同类别间混叠严重，说明了人为选取参数方法在变转速下诊断适应能力差，也证明了对多尺度一维卷积神经网络卷积核数量及尺度进行参数优化的重要性。

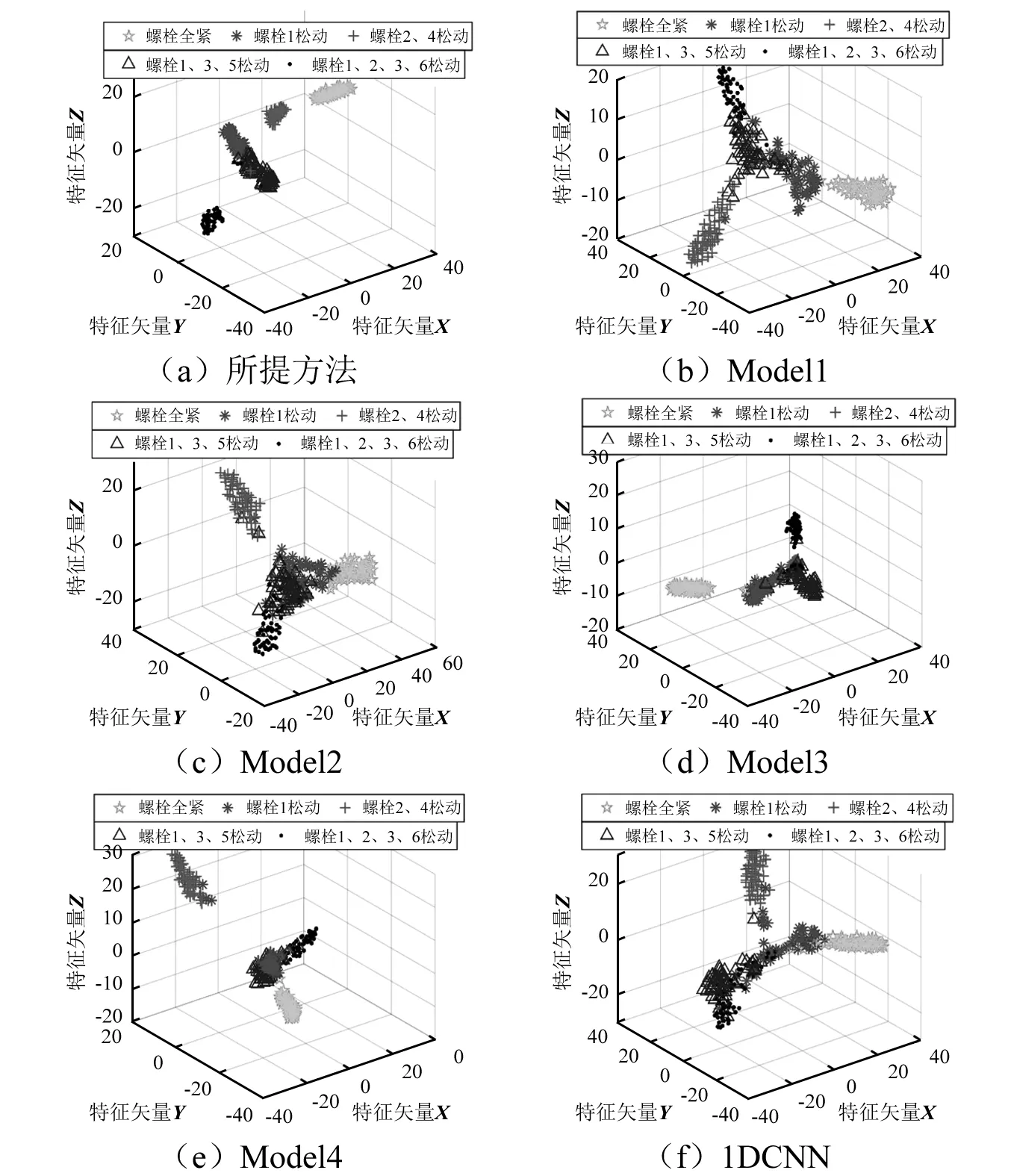
图10 学习特征t-SNE分析Fig.10 t-SNE analysis of learning features

4 结 论

提出PSO优化多尺度一维卷积神经网络的风机基础螺栓松动诊断方法将多尺度一维卷积神经网络中卷积核数目和尺度作为粒子群算法中的粒子，以验证精度作为适应度值，经过粒子速度和位置的不断更新，以获取最优卷积核数目和尺度参数，解决了多尺度一维卷积神经网络中卷积核数目和尺度依赖经验指导，需人工试验确定问题。

所提方法可在非经验指导下获取最优卷积核数目和尺度参数，针对实际工程中不同复杂程度的数据自适应确定最优网络参数，有效适应风机在稳定转速和升降速下一维原始振动信号特征提取，从原始信号中提取出有效松动特征，对信号特征充分表达。为风机基础螺栓松动诊断问题提供了一种新方法。