以绳连接模型为例谈关联速度的分析
■周 瑶
通过轻绳连接的不同物体,若在运动过程中的运动方向不都沿绳方向,则其速度虽不同,但必定存在某种联系,我们可以利用运动的合成与分解分析连接体的关联速度,下面举例分析。
1.常见的绳连接模型如图1所示。
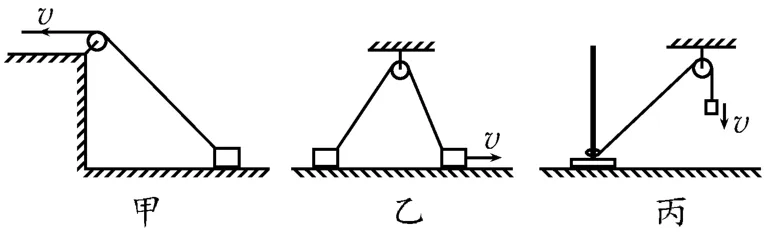
图1
2.绳连接模型的特点:连接体沿绳方向的速度分量大小相等。
3.连接体的合速度与分速度的关系:合速度是指物体的实际运动速度,分速度是指沿绳方向的分速度和垂直于绳方向的分速度,将两分速度按照矢量运算法则合成可以得到合速度。
4.求解绳连接模型中关联速度的方法:把物体的实际运动速度分解为沿绳方向和垂直于绳方向的两个分量,根据沿绳方向的分速度大小相等列式求解。
例1如图2所示,细线一端固定在天花板上的O点,另一端穿过一张光盘的中央小孔后拴着一个橡胶球,橡胶球静止时,竖直悬线刚好挨着水平桌面的边缘。现将光盘按在桌面上,并沿桌面边缘以速度v向左匀速移动,移动过程中,光盘中央小孔始终紧挨桌面边缘。当细线与竖直方向间的夹角为θ时,橡胶球上升的速度大小为( )。
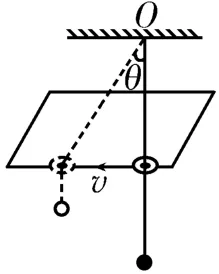
图2

解析
将光盘水平向左移动的速度v分解为沿桌面上方倾斜段细线方向的速度v1=vsinθ和垂直于这段细线方向的速度v2=vcosθ,橡胶球上升的速度大小与光盘速度v沿细线方向的分速度v1大小相等,故v球=vsinθ。
答案:A
点评
本题中光盘的速度v水平向左,可以分解到沿桌面上方倾斜段细线方向和垂直于这段细线方向上;橡胶球上升的速度v球沿细线方向,等于光盘速度v沿细线方向的分速度。
注意:处理绳连接体的关联速度问题时,一定要找到物体实际发生的运动(合运动),将合速度分解到沿绳方向和垂直于绳方向上,而不要分解分速度。
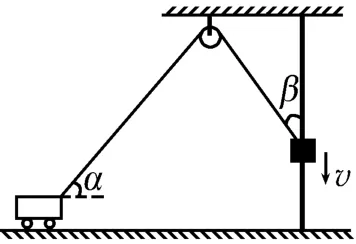
图3
例2如图3 所示,重物沿竖直杆下滑,并通过一根跨过定滑轮不可伸长的细绳拉动小车沿水平面向右运动。当定滑轮右侧的细绳与竖直方向成β角,且重物下滑的速度为v时,定滑轮左侧的细绳与水平方向成α角,则小车的速度为( )。

解析
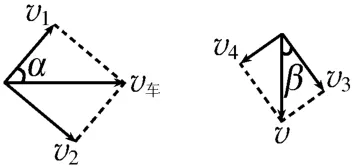
图4
小车的实际运动方向水平向右,重物的实际运动方向竖直向下,将小车的速度v车和重物的速度v按运动效果进行分解如图4 所示,则小车沿细绳方向的分速度v1=v车cosα,重物沿细绳方向的分速度v3=vcosβ。因为细绳不可伸长,所以重物和小车沿细绳方向的分速度大小相等,即v1=v3,解得v车=。
答案:D
点评
本题中重物和小车的速度都不沿细绳方向,需要先将两个物体的速度分别分解到沿细绳方向和垂直于细绳方向上,再利用两个物体沿细绳方向的分速度大小相等,建立关联方程,求出小车的速度。
拓展:同学们在平时的训练中还会遇到杆连接模型、弹簧连接模型或接触连接模型的关联速度问题,求解时可以借助上述处理绳连接模型关联速度问题的思路和方法。
感悟与提高
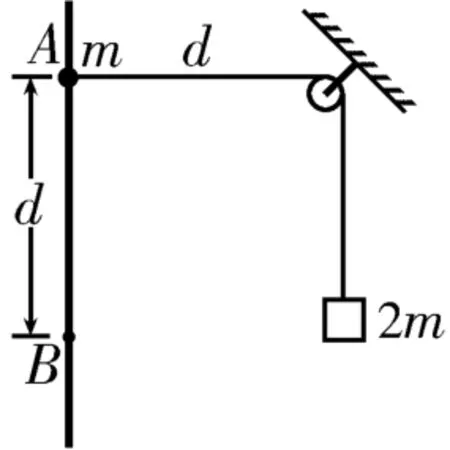
图5
1.如图5所示,将质量为2m的重物悬挂在轻绳的一端,轻绳的另一端跨过定滑轮系一质量为m的小环,小环套在竖直固定的光滑直杆上,光滑定滑轮与直杆间的距离为d。现将小环从与定滑轮等高的A处由静止释放,当小环沿直杆下滑的距离也为d时(图中B处),下列说法中正确的是(重力加速度为g)( )。
A.小环刚释放时,轻绳的张力一定大于2mg
B.小环到达B处时,重物上升的高度为(-1)d
C.小环到达B处时,小环的速度与重物的速度大小之比等于
D.小环到达B处时,小环的速度与重物的速度大小之比等于

图6
2.如图6所示,汽车A与木箱B位于同一水平地面上,一根轻绳跨过光滑定滑轮一端拴在汽车A上,另一端拴在木箱B上,汽车A水平向右行驶,通过轻绳拉动木箱B也向右运动,当二者运动到图示位置时,定滑轮两侧轻绳与水平方向间的夹角分别为α、β,二者的速度分别为vA和vB,则vA∶vB等于( )。
A.1∶1 B.sinα∶sinβ
C.cosβ∶cosαD.sinα∶cosβ
参考答案:1.ABD 2.C

