边收缩池化的网格变分自编码器
袁宇杰,来煜坤,杨洁,段琦,傅红波,高林*
1.中国科学院计算技术研究所, 北京 100190; 2.中国科学院大学, 北京 100049;3.英国卡迪夫大学,卡迪夫 CF24 4AG,英国; 4.商汤科技, 上海 200233; 5.香港城市大学, 香港 999077
0 引 言
近年来,互联网上的3D模型数据集呈现井喷式的发展。数据驱动的3D形状分析一直是计算机视觉和计算机图形领域的一个热门研究课题。除了传统的数据驱动工作(Gao等,2017),更多工作试图将深度神经网络方法从2D图像扩展到3D模型,如三角网格(Tan等,2018a,b;Litany等,2018)、点云(Qi等,2017a)、体素(Wu等,2016;Maturana和Scherer,2015)等。本文专注于三角网格的深度神经网络。与图像不同,三角网格具有复杂且不规则的连通性。大多数现有工作倾向于保持层与层之间的网格连接不变,从而失去了应用池化操作时增加感受野的能力。
变分自编码器(variational auto-encoder, VAE)(Kingma和Welling,2014)作为一种生成网络已广泛应用于各种任务,包括2维的人脸图像修复(张雪菲 等,2020)以及3维的三角网格的生成、插值和浏览(Tan等,2018b)。翟正利等人(2019)对变分自编码器模型及其衍生模型进行了综述。最初的MeshVAE(Tan等,2018b)使用全连接层,需要大量参数,泛化能力往往较弱。尽管全连接层允许层间网格连接的变化,但由于不规则的变化,全连接层后不能直接应用卷积层。一些工作(Litany等,2018;Gao等,2018)在 VAE结构中采用卷积层。然而,这样的卷积操作并不能改变网格的连通性。Ranjan等人(2018)在网格上的卷积网络中引入了采样操作,但其采样策略在减少顶点数量时不会聚合所有局部邻域信息。因此,为了处理更稠密网格的模型,增强网络的泛化能力,有必要设计一种类似于图像池化的网格池化操作形式,以减少网络参数的数量。此外,本文希望定义的池化可以支持进一步的卷积并允许通过相应的反池化操作恢复到原始网格。
本文提出一种具有新定义的池化操作的VAE架构,如图1所示。图中ε是随机变量,满足高斯分布N(0,I),I是全为1的向量,⊗和⊕分别表示乘和加。该方法使用网格简化的边收缩操作来形成具有不同细节层次的网格层次结构,并通过跟踪粗细网格之间的映射来实现有效的池化。为了避免在网格简化过程中生成高度不规则的三角形,引入了一种基于经典方法(Garland和Heckbert,1997)的改进的网格简化方法。新定义的池化操作能有效聚合局部邻域信息,增强网络的泛化能力。网络的输入是基于顶点的变形特征表示(Gao等,2021),与3D坐标不同,它使用定义在顶点上的变形梯度对变形进行编码。提出的框架使用一组具有相同连接关系的3D形状来训练网络。通过一致的重网格操作可以很容易地获得这样的网格。此外,本文在网络中采用了图卷积操作(Defferrard等,2016)。总体而言,本文提出的网络遵循VAE架构,其中应用了池化操作和图卷积。正如在实验部分展示的,本文网络不仅具有更好的泛化能力,而且可以处理更高分辨率的网格,从而有利于各种应用,如形状生成、插值和嵌入。
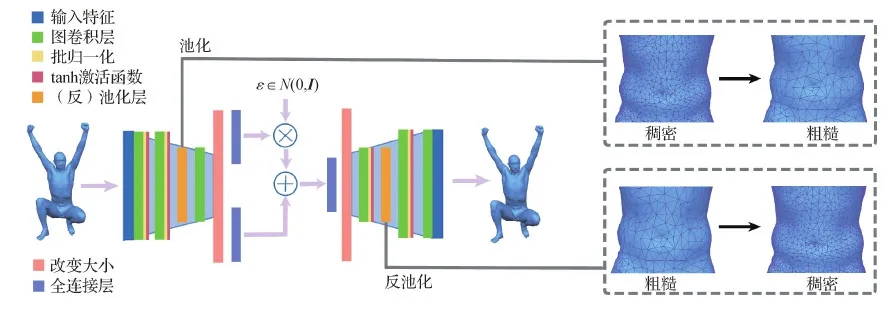
图1 本文网络结构Fig.1 Our network architecture
1 相关工作
1.1 3D模型的深度学习方法
针对3D模型的深度学习方法受到越来越多的关注。Boscaini等人(2016a,b)将卷积神经网络从欧几里德域推广到非欧几里德域,这有助于3D形状分析,比如建立3D形状之间的对应关系。Bronstein等人(2017)概述了在非欧氏域上利用卷积神经网络的方法,包括在图结构和网格上。Masci等人(2015)通过对以测地极坐标表示的局部面片应用滤波器,提出了第1个网格卷积运算。Sinha等人(2016)将3D形状转换为几何图像以获得欧氏参数化表示,标准的卷积神经网络即可被应用。Wang等人(2017,2018)提出了基于八叉树的卷积用于3D形状分析。与局部面片、几何图像或八叉树结构不同,本文工作使用顶点特征(Gao等,2021)为输入进行卷积运算。
为了分析具有相同连通性但不同几何形状的网格模型,MeshVAE(Tan等,2018b)首次将变分自编码器网络结构引入到3维网格数据,并通过各种应用证明了其有效性。Tan等人(2018a)使用卷积自编码器从具有大尺度变形的网格数据集中提取局部变形分量。Gao等人(2018)提出了一种将卷积网格变分自编码器与循环一致对抗网络CycleGAN (Zhu等,2017)相结合的网络,用于没有配对的形状之间的全自动变形传播。Tan等人(2018a)和Gao等人(2018)在网格上使用了基于空域的卷积运算,而Defferrard等人(2016)和Henaff等人(2015)的工作通过在频域的构造将卷积神经网络扩展到不规则图上,与空域卷积相比表现出更优越的性能。与Defferrard等人(2016)和Yi等人(2017)相同,本文工作也在频域中执行卷积运算。
虽然池化操作在图像处理的深度网络中得到了广泛的应用,但现有的基于网格的VAE方法有些不支持池化(Tan等,2018b;Gao等,2018),有些使用简单的采样过程(Ranjan等,2018),无法聚合所有的局部邻域信息。实际上,Ranjan等人(2018)提出的采样方法也是基于一种简化算法,但是该方法直接舍弃顶点,然后利用三角形的重心坐标通过插值来恢复丢失的顶点。相反,本文池化操作可以通过记录简化过程来聚合局部信息,并支持池化操作的直接逆向,从而有效地实现反池化操作。
Hanocka等人(2019)提出了MeshCNN,一种基于卷积神经网络(convolutional neural network, CNN)的网格神经网络,用于网格分类和分割。该框架包含一个动态网格池化操作,该操作根据特定任务进行网格简化。相反,本文在静态网格简化算法的基础上定义了池化操作,因为本文网络旨在编码和生成高质量的网格模型,静态简化算法保证了层次结构的一致性,从而更好地保留了几何细节,更具鲁棒性。
1.2 均匀采样或池化方法
以点云作为输入,PointNet++(Qi等,2017b)提出了一种均匀采样方法,能用于点云的神经网络中。基于相同的思想,TextureNet(Huang等,2019)对网格的顶点也进行均匀采样,但这种采样方法破坏了顶点之间的连接关系,将网格数据转化为点云,不支持进一步的图卷积。相反,简化方法可以建立网格层次结构,因此可以帮助执行网格池化操作。然而,大多数简化方法,如Garland和Heckbert(1997)都是保持几何形状的,但是简化网格上的顶点可能是高度不均匀的。重网格化操作(Botsch和Kobbelt,2004)可以构建均匀的简化网格,但会丢失层次结构中网格之间的对应关系。在经典方法(Garland和Heckbert,1997)的基础上,本文提出了一种改进的网格简化方法,对新定义的网格池化和反池化操作进行更均匀的网格简化,并记录粗糙网格和稠密网格之间的对应关系。
1.3 变形网格的表示和应用
为了更好地表示3D网格,一种直接的方法是使用3D形状的顶点坐标。然而,顶点坐标既不具有平移不变性,也不具有旋转不变性,这给大尺度变形的学习带来了困难。相反,本文使用了一种最新的3维形状变形表示方法(Gao等,2021),与另一种广泛使用的表示方法(Gao等,2016)相比,它具有在顶点记录变形,使得图卷积和池化操作更容易实现的优点。
2 方 法
2.1 网格简化
使用网格简化的边收缩算法来帮助构建可靠的池化操作。为此,网格简化不仅创建了具有不同细节级别的网格层次结构,而且还确保了较粗网格和较细网格之间的对应关系。网格简化过程基于经典的边收缩方法(Garland和Heckbert,1997),该方法根据衡量形状变化的度量依次重复边收缩操作。然而,原始方法不能保证简化的网格包含均匀分布的三角形。为了实现更有效的池化,较粗网格中的每个顶点都应对应于相似大小的区域。
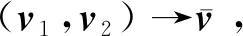
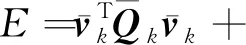
(1)
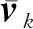
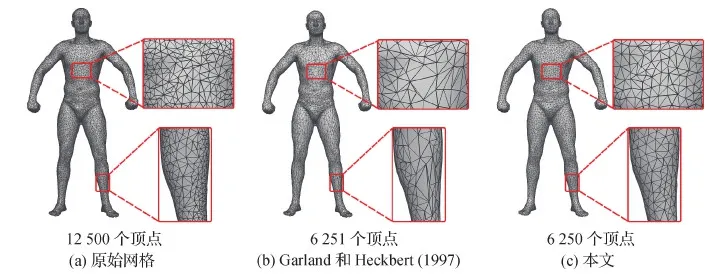
图2 比较网格简化算法Fig.2 Comparison of the mesh simplification algorithm ((a) original mesh; (b) Garland and Heckbert (1997); (c)ours)
2.2 池化和反池化
网格简化通过重复的边收缩操作来实现,即将两个相邻的顶点收缩为一个新的顶点。利用这个过程来定义网格池化操作。将采用平均池化应用于接下来的网络框架,其他类型的池化操作也可以类似地定义。在边收缩步骤之后,将新顶点的特征定义为收缩顶点的平均特征。如图3所示,通过边收缩将红色顶点简化为绿色顶点,并对红色顶点的特征进行平均,得到绿色顶点的特征。这确保池化操作在相应简化区域有效进行。这个过程有一些优点:它既保留了正确的拓扑结构以支持多层卷积或池化,也使感受野得到很好的定义。由于变分自编码器网络具有解码器结构,因此还需要正确定义反池化操作。同样利用了简化关系,将反池化定义为逆操作:简化后的网格上顶点的特征均等分配给稠密网格上相应的被收缩顶点。
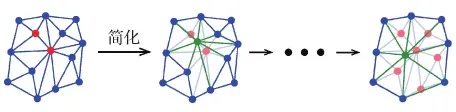
图3 使用简化算法来引入网格上的池化操作Fig.3 Using a simplification algorithm to introduce pooling operation on meshes
2.3 图卷积
为了形成一个完整的神经网络架构,采用Defferrard等人(2016)介绍的图卷积。假设输入是矩阵x,卷积操作的输出为矩阵y,其中x,y的每行对应一个顶点,每列对应一个特征维度。令L表示归一化图拉普拉斯算子。网络中使用的频域图卷积定义为
(2)
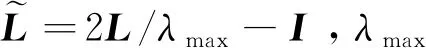
2.4 网络结构
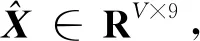
(3)
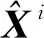
2.5 条件变分自编码器
当VAE用于形状生成时,通常倾向于选择生成形状类型,特别是对于包含来自不同类别的形状的数据集(例如男性和女性,瘦和胖,更多示例参见Pons-Moll等人(2015))。为了实现这一点,参考Sohn等人(2015)为输入和隐变量添加标签以扩展框架。在这种情况下,网络的损失函数变为
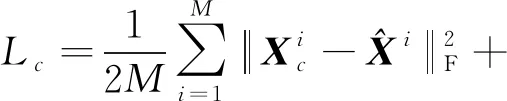
(4)
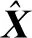
2.6 实现细节
在所有的实验中,式(1)中用λ=0.001收缩一半的顶点,并设置图卷积式(2)的超参数H=3,总损失函数中α=0.3。除了特别说明的实验,其余实验的隐空间维度都是128,并在网络权重上使用L2正则化来避免过度拟合。使用Adam优化器(Kingma和Ba,2015),其中β1=0.9,β2=0.999,学习率设置为 0.001。
3 实验结果与分析
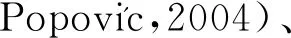
3.1 架构评估
为了比较不同的网络结构和设置,同时对编码解码结果的性能有较大影响的一些因素分析,进行一系列消融实验。
1)池化的影响。在表1(第8列和第3列)中,比较了在使用和不使用池化的情况下重建形状的RMS误差。使用池化后RMS误差平均降低6.92%。该结果显示了池化和反池化操作的优势,能增强网络在未见形状上的重建能力。

表1 消融实验的RMS重建误差Table 1 Ablation study of RMS reconstruction errors
2)与空域卷积比较。将频域图卷积与空域图卷积进行比较,二者都采用了如图1所示的网络结构。比较结果如表1(第2列和第3列)所示,容易发现频域图卷积得到了更好的结果,这是因为频域卷积相较于空域卷积,能考虑更多的邻域信息。
3)与其他池化或采样方法比较。为了证明基于改进的边收缩算法的池化操作的优势,将提出的池化与基于原始简化算法(Garland和Heckbert,1997)的池化、基于均匀重网格方法(Botsch和Kobbelt,2004)的池化、现有的图池化方法(Shen等,2018)和网格采样操作(Ranjan等,2018)进行了比较。其中,重网格方法能够均匀地分布顶点,但会丢失几何细节。而本文方法旨在实现均匀的同时保持形状的简化,从而获得更好的泛化能力。结果如表1所示。与基于Garland和Heckbert(1997)的池化相比,本文池化对训练未见数据的RMS误差平均降低了9.34%,与均匀重网格方法(Botsch和Kobbelt,2004)相比降低了9.07%,与图池化方法(Shen等,2018)相比降低了8.06%,与网格采样操作(Ranjan等,2018)相比降低了9.64%。结果表明,改进后的简化算法在池化方面更为有效,而且本文方法的池化在多个数据集上的效果更为优越,展示了其泛化能力。另外,图4展示了改进的简化算法与原始简化算法在简化网格上的更多比较结果,可以看出改进的边收缩算法能够得到分布更均匀的简化网格。这也是本文网格池化在数值上具有优势的原因。
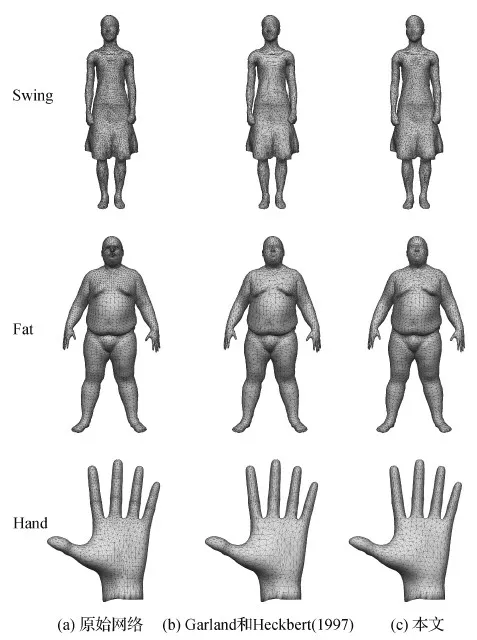
图4 与经典网格简化算法的更多对比Fig.4 More comparisons with the mesh simplification algorithm ((a) original mesh; (b) Garland and Heckbert (1997); (c) ours)
3.2 与最优方法的比较
在表2中,将本文方法与最先进的基于网格的自编码器架构(Gao等,2018;Ranjan等,2018;Tan等,2018b)在重建未见形状的RMS误差方面进行了比较。由于使用了频域图卷积和本文池化操作,该方法减少了训练未见数据的重建误差,展现出优越的泛化能力。例如,与使用相同逐顶点特征的Gao等人(2018)方法相比,本文网络在SCAPE和Face数据集上降低了29%和32%的平均RMS重建误差。此外,在图5—图7与Gao等人(2018)和Ranjan等人(2018)方法进行了重建的可视化比较。图5和图6中重建误差使用颜色可视化。这些结果表明,本文方法比Gao等人(2018)和Ranjan等人(2018)方法能够生成更加准确的重建结果。
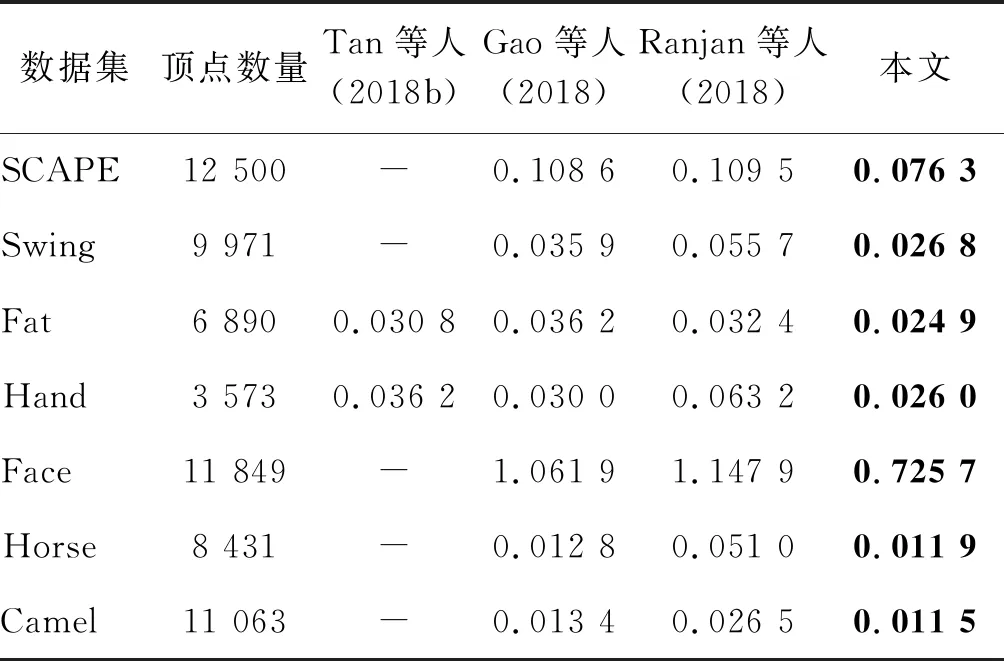
表2 与不同自编码器框架比较训练未见数据的RMS重建误差Table 2 Comparison of RMS reconstruction errors for unseen data using different auto-encoder frameworks
在表3中还与MeshCNN(Hanocka等,2019)进行了比较。MeshCNN使用边上的特征,包括每个面的二面角、两个内角和两个边长比作为输入,不能用于重建模型。因此,采用边特征的平均绝对误差(mean absolute error, MAE)作为比较的度量。为本文网络的输入形状和重建形状计算这些特征,并修改MeshCNN的分割网络用于编码和解码任务。可以看到,网络在所有的5个边特征上都取得了更好的结果,这反映了本文方法重建的网格三角形质量更好。
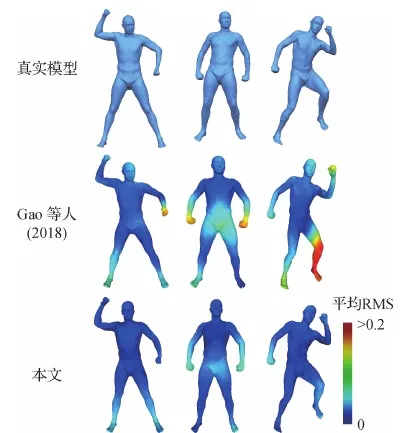
图5 与Gao等人(2018)方法的重建结果可视化比较Fig.5 Qualitative comparison of reconstruction results with Gao et al.(2018)
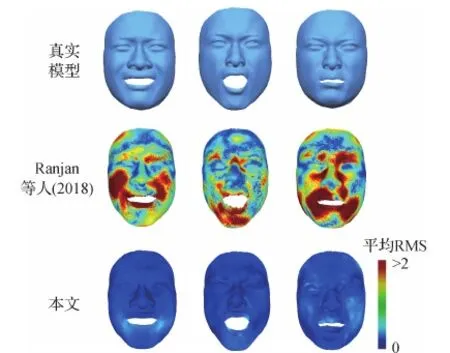
图6 在训练未见数据上重建结果可视化比较Fig.6 Qualitative comparison of reconstruction results for unseen data
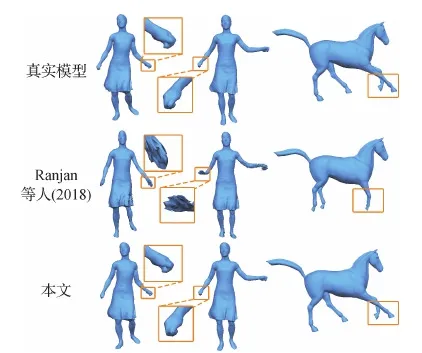
图7 与Ranjan等人(2018)方法的重建结果可视化比较Fig.7 Qualitative comparison of reconstruction results with Ranjan et al.(2018)
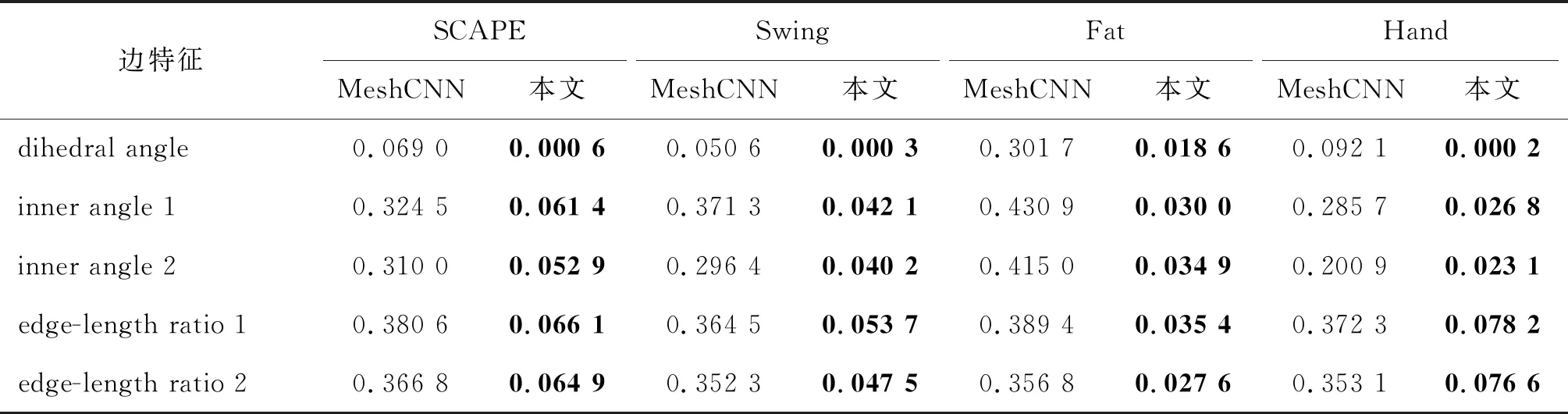
表3 与MeshCNN(Hanocka 等,2019)比较MAE重建误差Table 3 Comparison of MAE reconstruction errors with MeshCNN (Hanocka et al.,2019)
在表4中,与DEMEA(deep mesh autoencoder)(Tretschk等,2020)进行比较,采用与DEMEA相同的数据集以及训练集和测试集划分,网络使用相同的隐含层维度32维。结果度量上也采用了与DEMEA相同的平均逐顶点误差。从表中结果比较可以看出,在4个数据集上,本文网络都取得了更好的重建结果。
表5实验说明本文网络比原始MeshVAE需要的参数更少。在Fat和Hand两个数据集上,本文网络需要的网络权重数量远远少于原始的MeshVAE,这更有助于网络的泛化能力。
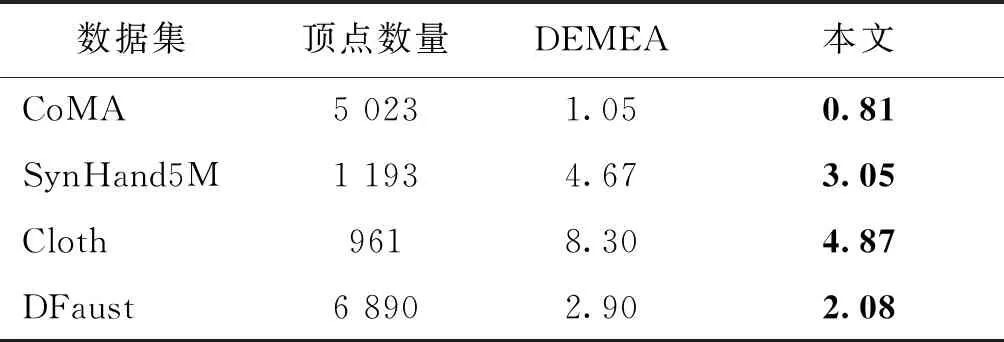
表4 与DEMEA(Tretschk等,2020)比较重建误差Table 4 Comparison of reconstruction errors with DEMEA (Tretschk et al., 2020)

表5 与原始MeshVAE(Tan 等,2018b)在网络权重数量上的比较Table 5 Comparison of parameters number withMeshVAE (Tan et al., 2018b)
3.3 新形状生成
网络训练完成后就可以使用隐空间和解码器来生成新的形状。使用标准正态分布zN(0,1)作为输入传入训练好的解码器。从图8可以看出,本文网络能够生成合理的新形状。为了证明生成的形状不存在于数据集中,根据顶点平均欧氏距离找到训练数据集中最相近的形状用于视觉比较。从比较可以看出生成的形状确实是新的,不同于训练数据集中任何已有的形状。为了展示模型的条件随机生成能力,在Pons-Moll等人(2015)的Dyna数据集上训练网络。分别使用BMI(body mass index)+性别和运动作为条件来训练网络。如图9所示,本文方法能够随机生成以编号“50007”,一个BMI为39.0的男性模型为条件,和以带有“单腿跳跃”标签的动作(包括抬腿)为条件的新形状。
3.4 形状插值
本文方法也可用于形状插值。这也是一种生成新形状的方法。将两个形状的隐变量进行线性插值,然后利用概率解码器输出3D变形序列。在SCAPE数据集(Anguelov等,2005)上与原始MeshVAE和最先进的数据驱动变形方法(Gao等,2017)进行对比,结果分别如图10和图11所示,最左列和最右列中的模型是插值的输入模型。可以看到MeshVAE生成的插值结果具有明显的瑕疵。Gao等人(2017)的结果倾向于遵循原始数据集的运动序列,这些数据集具有相似的开始和结束状态,这导致如摆动右臂等多余的运动。相比之下,本文插值给出了更合理的运动序列。在图12中,展示了与Litany等人(2018)方法的比较,其会产生瑕疵,特别是在合成的人手中。在图13展示了更多的插值结果,包括在新生成的人体模型之间和其他类型的模型之间插值。

图8 本文框架随机生成的新形状以及它们在原始数据集中的最近邻Fig.8 Randomly generated new shapes by our framework, along with their nearest neighbors in the original datasets ((a) Hand; (b) SCAPE; (c) Horse; (d) Face; (e) Swing)
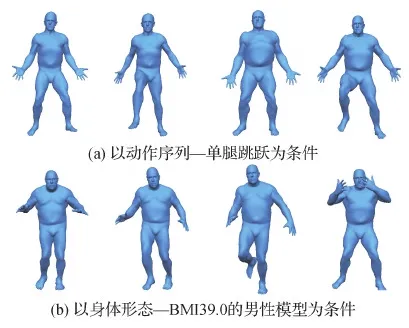
图9 本文框架条件随机生成新形状Fig.9 Conditional random generation of new shapes using our framework((a) conditioned on motion sequence—one leg jump; (b) conditioned on bodyshape—male model with BMI 39.0)
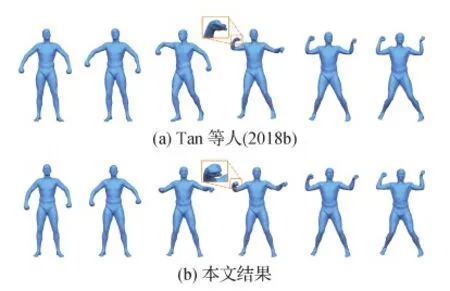
图10 与Tan等人(2018b)比较网格插值结果Fig.10 Comparison of mesh interpolation results with Tan et al.(2018b)((a) Tan et al.(2018b); (b) ours)
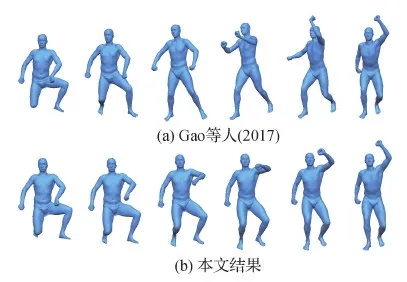
图11 与Gao等人(2017)比较网格插值结果Fig.11 Comparison of mesh interpolation results with Gao et al.(2017)((a) Gao et al.(2017);(b) ours)
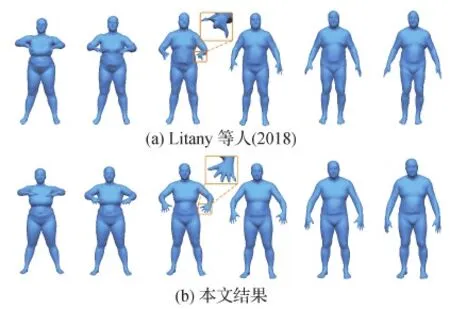
图12 与Litany等人(2018)比较网格插值结果Fig.12 Comparison of mesh interpolation results with Litany et al.(2018)((a) Litany et al.(2018); (b) ours)
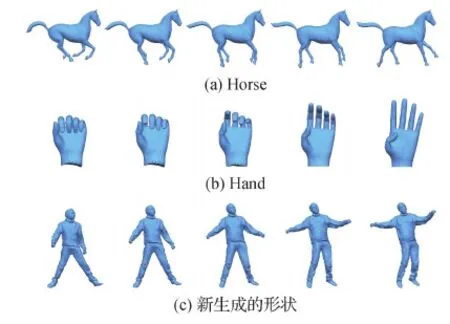
图13 更多插值结果Fig.13 More interpolation results((a) Horse; (b) Hand; (c) new generated shapes)
3.5 形状嵌入
本文方法可以将3D形状压缩成低维向量进行可视化。为了更好地可视化嵌入,计算了隐含向量的最大的两个方差作为2D嵌入图中模型对应的水平和垂直坐标,利用这种方法在低维空间中嵌入形状。本文方法根据模型的形状来划分所有的模型,同时允许相似姿态的模型保持在接近的位置。使用一个代表性的运动序列,即来自Sumner和Popovi(2004)的马运动序列。Horse数据集包含一个奔腾的马的运动序列,它形成了一个循环序列。可以从图15左子图所示的嵌入结果,即一个与原始序列相匹配的圆得出结论,本文网络具有良好的嵌入能力。在图15的右上角和右下角,还分别展示了PCA(principal components analysis)和t-SNE(t-distributed stochastic neighbor embedding)的结果。对比发现,本文网络结果呈现为两个圆,而PCA和t-SNE不能揭示数据的内在信息。
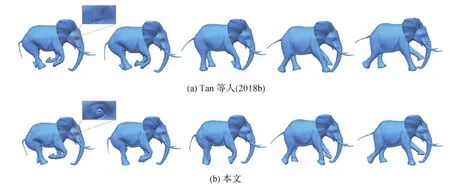
图14 与MeshVAE(Tan等,2018b)的插值比较Fig.14 Interpolation comparison with MeshVAE ((a) Tan et al.(2018b); (b) ours)
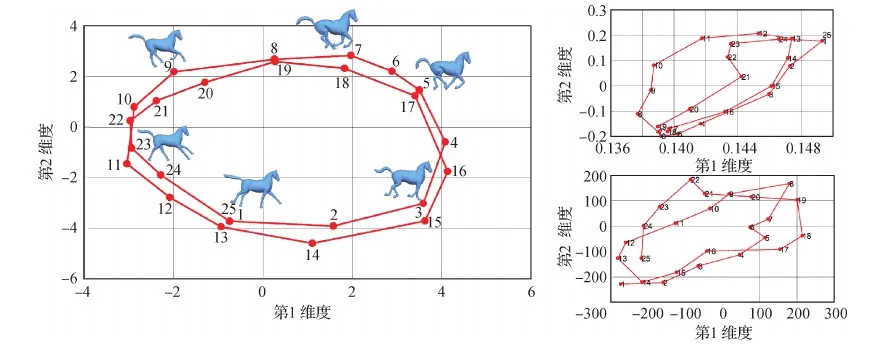
图15 Horse数据集(Sumner和的2D嵌入Fig.15 2D embedding of Horse dataset (Sumner and 2004)
4 结 论
本文提出了一种新的网格池化操作,该池化操作能改变网格的连接关系,支持进一步的卷积或池化操作。该池化操作基于边收缩网格简化算法。同时,为了使得网格池化的感受野更加一致,改进了边收缩网格简化算法。利用提出的网格池化操作,结合图卷积算子,本文构建了一个网格变分自编码器,该网络采用逐顶点特征表示作为输入。通过对训练未见数据的重建实验,表明了相较于目前已有的网格编解码网络,本文网络具有更好的泛化能力。相较于原始的MeshVAE,方法能够生成高质量且具有丰富细节的变形模型。模型还可以被应用于包括形状生成,形状插值和形状嵌入等诸多应用中,且实验表明,模型超越了已有方法。不足之一在于只能处理相同连接关系的网格结构,这是由于神经网络的输入需要一致的表示。又因为池化操作是基于网格简化的,因此在网格简化失败的情况下无法生成合理的结果,例如非水密网格和高度不规则的网格输入。对于未来的工作,拟探索如何将不同拓扑结构的网格作为输入,同时在网格简化算法上进一步研究,解决网格简化失败导致网格池化无法使用的情况。

