三维点云配准方法研究进展
李建微,占家旺
福州大学物理与信息工程学院,福州 350116
0 引 言
3维数据是一种现实物理世界的重要表达方式,有多种表现形式,包括深度图像、多边形网格和点云(Guo等,2014)等。3维点云数据获取设备如激光雷达等产品的成熟和普及以及计算机运算能力的提升,使点云数据得到了广泛应用。点云配准技术是点云数据处理中一个极具挑战性的研究方向,因为点云是一种非结构化的数据形式,存在遮挡和噪声(Duan等,2021)以及较大的数据量(Sultani和Ghani,2015),并且需要精确快速地完成。本文主要研究点云的刚性配准,即可以只通过平移和旋转操作将点云配准,而没有缩放和变形。点云配准技术是多个领域的重要技术,包括移动机器人的同步定位和制图(simultaneous localization and mapping,SLAM)、自动驾驶中使用的高精度地图构建和环境感知、森林结构参数评估、自动城市建模、增强现实(augmented reality,AR)的景物检测、医学检测的图像合成、施工监控和竣工建模等众多应用场景。这些应用场景往往需要很高的配准精度,有些则需要很快的配准速度。精度高且速度快的配准算法能够极大地提高这些应用的性能。
点云配准算法在20世纪70年代就已有研究。ICP(iterative closest point)是一种最经典的点云配准算法(Besl和Mckay,1992),通过迭代对应点搜寻和最小化点对整体距离以估计变换矩阵。因为是非凸的,所以容易陷入局部极小值。当点云配准需要较大的旋转平移时,ICP往往无法得到正确的结果。NDT(normal distributions transform)是另一种经典的精配准方法,通过最大化源点在目标点体素化后计算出的正态分布的概率密度上的得分进行配准(Magnusson等,2007)。ICP、NDT算法及其变体需要点云已经大致对齐,或者是有IMU(inertial measurement unit)、GNSS(global navigation satellite system)、里程计等先验位姿,否则需要粗配准为其提供一个初始位姿(Ilci和Toth,2020)。简单的点与点的对应不具有鲁棒性,所以接下来很多工作都致力于寻找更加鲁棒的对应,如点对面、面对面和特征对特征。通过这些对应关系估计配准参数,这些对应关系提高了点云配准的正确率,降低了对正确初始位姿的依赖。具有更多信息的对应关系可以用于点云粗配准,典型的粗配准由特征检测、特征描述和特征匹配等构成(Bueno等,2017)。特征检测减少总的点数,保留独特性高的部分;特征描述旨在将高维的特征信息转换为低维度但却依然易于分辨和对比的描述子;特征匹配寻找特征之间的对应关系,一旦建立对应关系配准问题就变成了一个凸问题,变换估计就变得更容易。另一种粗配准的方法基于全等四点集(4-points congruent sets)(Aiger等,2008),在刚性变换下,部分点的变换也是全部点的变换,通过验证多组全等集得到最佳变换。传统的非学习点云配准方法对硬件要求低、易于实施、可解释性强且不需要耗时的训练过程,但是却存在容易陷入局部极小值或通用性不好的问题,使用手工特征区分对应关系,受设计者经验和参数调整能力的影响很大。另外粗配准方法往往都比较耗时,在一些实时应用中可能会遇到瓶颈。
近年来,深度学习取得了很多进展,越来越多的算法都通过深度学习获得了性能上的进步,深度学习在点云配准任务中也得到了广泛应用(Liu等,2019)。很多算法都获得了速度提升,并且表现出对噪声、低重叠以及遮挡的鲁棒性。基于学习的方法在性能提高上表现出的潜力使其成为当前点云配准领域热门的研究方向。在点云上进行学习需要克服点云的噪声和遮挡,更大的挑战在于点云的非结构化、无序性和不规则性,这就不利于将成熟的结构化的图像方法推广到点云上。于是,基于体素的方法、基于多视图的方法和在原始点云直接进行学习的方法得以用于点云上的学习(Bello等,2020)。基于学习的点云配准与非学习的方法有很多共通之处,很多基于学习的点云配准算法都是在非学习的配准算法的基础上,用网络代替其中的一部分,或是完全由网络组成端到端的算法,所以基于学习的方法往往是非学习方法和深度学习理念的结合。多数基于学习的点云配准方法是基于特征的,但是学习到的特征对比人工设计的特征具有更好的通用性、鲁棒性和描述能力。基于学习的方法还能够学到更高级、更多层次的描述符,对特征选取和特征表示以及点密度和测量角度差异更加鲁棒(Dong等,2020)。通过GPU(graphics processing unit)的并行计算能力,基于学习的点云配准方法具有速度上的优势,特别是在粗配准方面有很大优势。但是基于学习的方法对比非学习方法往往需要更多的计算资源,有实时要求但计算资源很有限时,不适合使用基于学习的方法。
在点云配准方面已有综述性工作,Pomerleau等人(2015)总结了ICP及其改进算法;Díez等人(2015)专注于点云的非学习粗配准方法;Cheng等人(2018)将点云配准的方法分为精配准方法和粗配准方法,但是都没有涉及基于学习的方法;Dong等人(2020)也将点云配准的方法分为精配准方法和粗配准方法,并且涉及了一些基于学习的粗配准方法,但是篇幅较小。目前还没有检索到中文的点云配准方法的综述总结基于学习的方法。本文将点云配准方法分为非学习的方法和基于学习的方法,并将非学习方法分为经典方法和基于特征的方法,将基于学习的方法分为结合非学习方法的部分学习方法和直接的端到端学习方法。目前,点云配准技术仍然很受重视,并且在继续快速发展,并不断取得新的进步。
1 非学习的点云配准方法
1.1 经典点云配准方法
1.1.1 ICP及其变体
标准 ICP 算法,即点对点—迭代最近点(point to point iterative closest point,P2P-ICP)算法的数学模型为:给定源点云P={p1,p2,p3,…,pm}⊂R3和一个与之对应的目标点云Q={q1,q2,q3,…,qn}⊂R3,其中m和n分别为源点云和目标点云的点的个数。
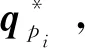
(1)
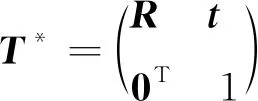
(2)
求出的T*可以再代入式(1),通过式(1)和式(2)迭代寻找最近点,并通过最小化点间欧氏距离平方和估计变换矩阵,当达到要求的误差或超过设置的迭代最高次数则终止迭代,通过将每一次的T*施以矩阵的乘法获得最终的变换矩阵。这种方法在面对点云巨大、具有大量噪声和离群值、点云密度变化和点云结构复杂时没有良好的表现。研究者提出了许多ICP的变体以应对这些挑战。
一些方法致力于提高ICP方法的精度。Chen和Medioni(1992)将点对点扩展到点对面(point to plane,ICP),通过计算法线得到一个切平面,通过最小化点到切平面的距离达到配准效果,这使其对点云的噪声有更好的适应性。Segal等人(2009)提出了一种面对面(generalized iterative closest point,GICP)的方法,将迭代最近点和点对面ICP算法结合到一个概率框架中,将点对点和点对面方法都变成了它的一种特殊情况。该方法在两个点上建立高斯分布,这样对于经过任意的刚体变换T后,两个点间的距离就有了一种高斯分布,那么最优的变换矩阵就是使对应点间经此变换后距离的高斯概率最大的变换矩阵。此方法对错误对应具有鲁棒性,并且还可以允许添加离群项、测量噪声和其他概率技术来增加鲁棒性。一些方法致力于扩大ICP方法的收敛范围。Gold等人(1998)提出RPM(robust point matching),通过将点对应关系从一对一变成一对多,并通过确定性退火在每次迭代时逐渐“强化”分配。其中退火参数较小时对应更平均,这有助于避免陷入局部最小值,而β增加时更趋向于只对应某一个。Yang等人(2013)提出go-ICP算法,通过分支定界法,在SE(3)空间内,使用八叉树数据结构将初始空间细分为较小的子空间,用分支定界的方法去除不佳的空间,继续细分满足门限条件的空间,从而找到全局最优变换。该方法尽管解决了局部极小值问题,但对初始化仍然很敏感。Liu等人(2020)提出MVGICP(multi-scale voxelized generalized iterative closest point),在迭代的大尺度到小尺度的体素上计算体素内的均值和方差,然后将其代入GICP模型中,并利用高斯牛顿方法得到变换矩阵,然后继续以更小的体素进行迭代。较大的体素可以更加全局地粗略配准点云,而较小的体素可以进一步提高配准结果的精度。并且也不需要最邻近搜索,因此可以显著提高计算效率。另一些方法致力于提高ICP的效率,Simon等人(1995)提出一种基于解耦加速的ICP算法,通过kd-tree以及根据上一次最近点搜寻的结果推断此次可能的位置,通过最近点高速缓存,加快搜寻。通过解耦,尽可能独立地加速平移和旋转,而不会产生冲突。Pavlov等人(2018)将Anderson加速引入ICP算法(Anderson acceleration iterative closest point,AA-ICP),利用Anderson算法对不动点问题的加速能力,还提出了两种启发性的策略以应对Anderson算法的不稳定性的问题,提高了配准的收敛速度和鲁棒性。ICP算法也可以与特征相结合,Ren和Zhou(2015)用容易获得的拐点特征代替点,减少了点的数量,在大规模数据点云上显示出优势。
ICP是最简单常用的配准算法,ICP及其多数变体都依赖于良好的初始位姿,以防止陷入局部最优。很多算法减轻了这种依赖,但是却不能彻底解决这种依赖。由于对应匹配的配准策略,不正确的对应对配准影响很大但是却非常普遍,从而限制了配准的准确性。
1.1.2 NDT及其变体
NDT点云配准方法是另一种经典的点云配准方法,是一种利用数学分布性质刻画点云数据并用其构造优化目标的方法(Magnusson等, 2007)。用于点云配准的3D NDT是受Biber和Strasser(2003)提出的2D NDT算法的启发,并将其扩展到3D。给定源点云P={p1,p2,p3,…,pm}⊂R3和目标点云Q={q1,q2,q3,…,qn}⊂R3,经典的NDT算法对目标点云进行体素化,然后计算体素内的点的均值μ和方差Σ,具体为
(3)
(4)
这样可以得到一个描述体素内点分布情况的概率密度函数,并且不需要在每次迭代时重新计算。具体为
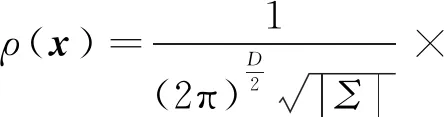
(5)
最佳的变换矩阵使源点云在其对应的概率密度函数中的整体似然达到最大,具体为
(6)
将最佳的变换作用于源点云,迭代式(6)计算新的最佳变换。NDT方法对体素的划分敏感,可以通过改变体素的大小,对收敛精度和速度进行调整。但是因为其成本函数会由于点跨越体素边界而不再连续,因此优化收敛性较差。Das和Waslander(2012)提出一种多尺度K均值NDT(multi-scale K-means normal distributions transform,MSKM-NDT),根据K均值聚类划分点云,并且在多个尺度上进行优化,K均值聚类解决了NDT算法中出现的成本函数不连续问题。多尺度优化有利于跨越局部最小值,这也改善了这种方法的收敛性。Lu等人(2015)提出一种体素大小可变的方法,在将大体素分割为几个小的体素的过程中考虑体素内点的个数,点稀疏时体素分大些,点密集时体素分小些。这样可以将稀疏点聚集为一个大的体素,将密集的点分散为多个小体素,从而消除了固定大小的体素之间的点的数量差异很大的问题,避免了某些稀疏点无法使用的缺陷。Das和Waslander(2014)提出一种分段区域生长NDT算法(segmented region growing normal distributions transform,SRG-NDT),使用基于高斯过程的分割算法从扫描中删除地平面,然后应用效率高的区域增长算法对其余点进行聚类,不再是按体素进行概率密度函数的计算,而是从聚类的结果中计算概率密度函数,从而得到比体素方法少得多的概率分布来对环境进行精确建模,同样也克服了成本函数的不连续性,并且由于除去了地面点,从而使速度得到明显提高。Zaganidis等人(2017)利用点云的平滑度将点云分区,丢弃掉未划分进分区的大量点,不在全部点云而是在相同类型的分区上进行NDT,这既减少了点的数目又为配准剔除了一些干扰,不仅加快了配准速度,也提高了鲁棒性。
与ICP类算法一样,NDT算法也是一种可以达到精配准的方法,并且因其不需要显式计算最近邻近对应点,所以NDT算法比ICP算法更快。但是NDT及其变体依然需要良好的初始位姿,否则也容易陷入局部极值。
1.1.3 4PCS及其变体
4PCS算法是一种经典的点云粗配准方法,该方法是基于RANSAC(random sample consensus)算法的理念设计的(Aiger等, 2008)。给定源点云P={p1,p2,p3,…,pm}⊂R3和目标点云Q={q1,q2,q3,…,qn}⊂R3。将点云配准问题变成在Q上寻找所有大致与P中选取的基共面四点集相近似的共面四点集,然后验证由这些相似共面四点集计算得出的变换矩阵,选取最佳的变换作为最终结果。具体步骤为:1)在P中选取基共面四点集,计算4点构成两个相交直线的交点并记为e,两条线段的长度记为d1和d2,并分别计算两条直线被交点分成的两段的长度的比值,记为r1和r2;2)在Q中分别寻找所有距离约等于d1或d2的点对,并分别记为R1和R2。根据r1计算R1中点对可能的交点位置,用交点建立范围树结构(range tree structure,RS)。根据r2计算R2中点对可能的交点位置,并对每个交点在范围树结构中寻找大致接近的交点,由此可以确定一个大致一致的共面四点集;3)为每一对一致的共面四点集计算变换矩阵并作用于P,然后计算P中的点到Q中点的距离小于阈值δ的点数,最佳变换是使最多点靠近的变换。
4PCS算法是一种粗配准方法,不需要提供初始位姿,而能够为精配准方法提供一个良好的初始位姿。4PCS算法可以应对点云的噪声和遮挡,即使对少量异常值“污染”的点云数据,也无需进行过滤和去噪,在大多数情况中都可以有不错的表现。4PCS算法的主要问题在于比较慢,提取相似集和验证变换都比较耗时,4PCS在数据点数量上具有二次时间复杂性。
很多研究致力于提高4PCS算法的速度。Mellado等人(2014)提出super 4PCS算法。在4PCS算法中判断是否是大致一致共面四点集,只根据两条直线被交点分成的两段的长度的比值,而没有考虑两条线之间的夹角,super 4PCS考虑了这一点,这减少了候选大致一致共面四点集的数量。对于提取所有距离约等于d1或d2的点对和夹角匹配,super 4PCS分别借用3D球体与点之间的经典入射问题和报告位于圆上的所有点在单位球上的入射问题的思路,将搜寻速度大幅提高,在数据点数量上达到一次时间复杂性。Huang等人(2017)提出了volumetric 4PCS,将4个共面点扩展为非共面点以进行全局配准,之所以使用非共面4点是因为当形状接近于平面时,还使用共面点会导致太多点满足与基共面四点集相似,找到这些点集耗时,验证这些点集也很耗时。volumetric 4PCS在super 4PCS的基础上进行改进,继承了其快速的优势。因为是非共面四点集,所以需要6个点间距离来描述基四点集的信息,所以需要找大致满足6个点间距离的点集合然后验证,得到最佳变换。Mohamad等人(2014)提出允许4PCS中本应该相交的两条线落在不同的平面上,允许两个线段之间有任意的距离和任意的分离度,增加分离度的方法使搜索空间有了指数级的减少,使运行效率比4PCS有了一个很大提高。Fotsing等人(2020)将在完整点云上进行的4PCS改进为将从源点云和目标点云划分出的平面对之间的4PCS,大幅减少了数据量的大小和执行时间。在验证变换时,不同于4PCS使用最大公共点集(large common plansets,LCP)衡量配准质量,该算法使用最大的公共平面集代替,这使验证速度更快,并对噪声更鲁棒。Xu等人(2019)提出voxel 4PCS,将点云体素化用以提取平面,再将共面平面融合,用平面代替点,用角度关系代替长度关系作为在刚性变换中不变的关系判别特征的相似性,实现了更高的鲁棒性和速度。4PCS算法的另一种变体是将特征引入4PCS算法。
4PCS算法及其变体作为一种粗配准方法,具有对噪声、遮挡和异常值的鲁棒性,不需要初始位姿。其主要的限制还是在于寻找几何形状相似的点集,验证由这些点集确定的变换矩阵都需要比较大的计算量,导致计算时间较长,虽然其变体在一定程度上加快了速度,但仍无法满足一些实时性要求高的应用。
表1总结了经典的ICP、NDT、4PCS算法及其变体的典型算法和优缺点。
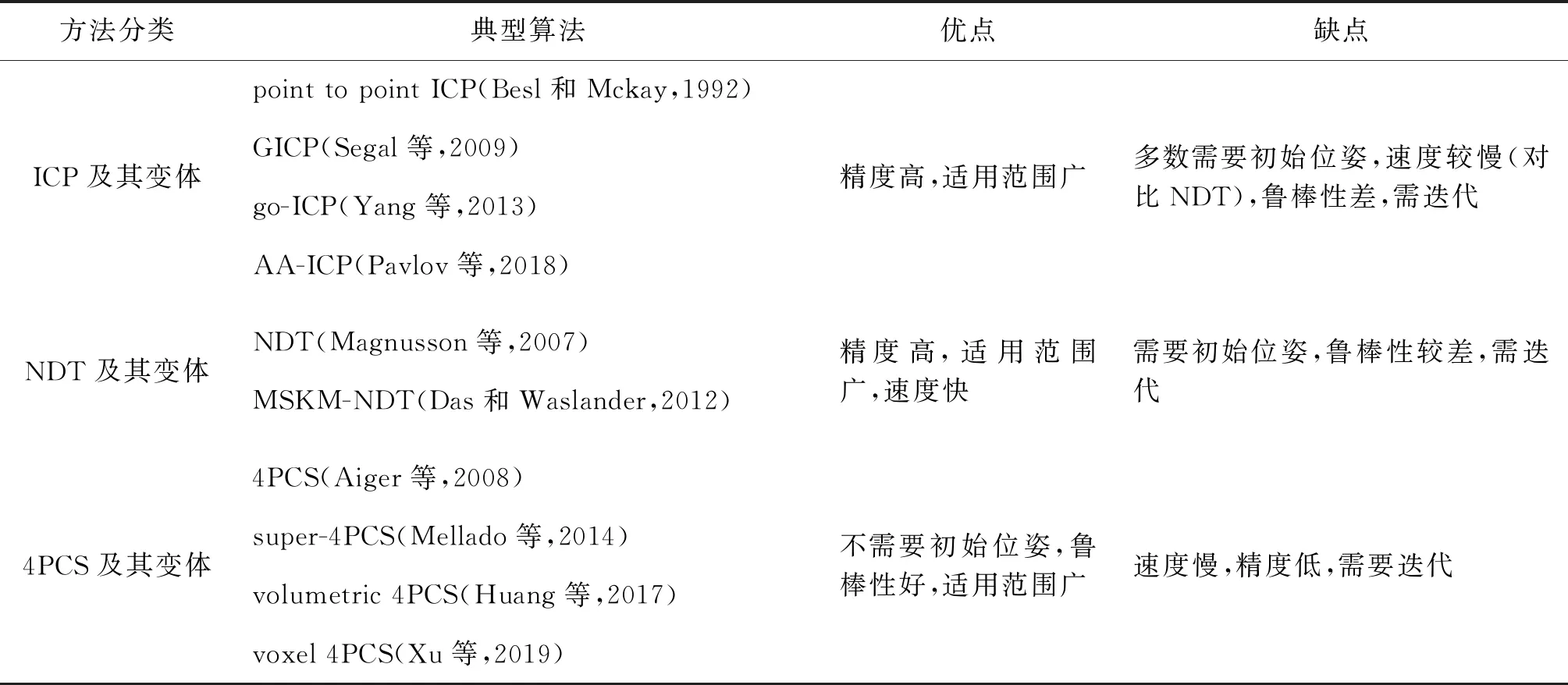
表1 经典点云配准算法Table 1 Classic point cloud registration algorithm
1.2 基于特征的点云配准方法
基于特征的方法没有用点云中全部的点进行配准,而是只选取点云中比较特殊的一部分进行配准,这种方法可以不需要提供初始位姿,并且具有鲁棒性。一个典型的基于特征的点云配准方法包括特征检测、特征描述和特征匹配。其中,特征检测使要处理的数据量变少,从而加快配准过程;特征描述将不容易进行对比的特征信息变换成容易对比的信息,从而有利于关键点的匹配;特征匹配用于找到源点云和目标点云的特征之间的正确对应关系,从而计算出变换矩阵(Díez等, 2015)。典型的基于特征的点云配准方法的流程图如图1所示,但是并不是所有的方法都是这样的结构,点云预处理和特征描述有时不是必要的,而特征匹配和变换估计可能需要多次执行。
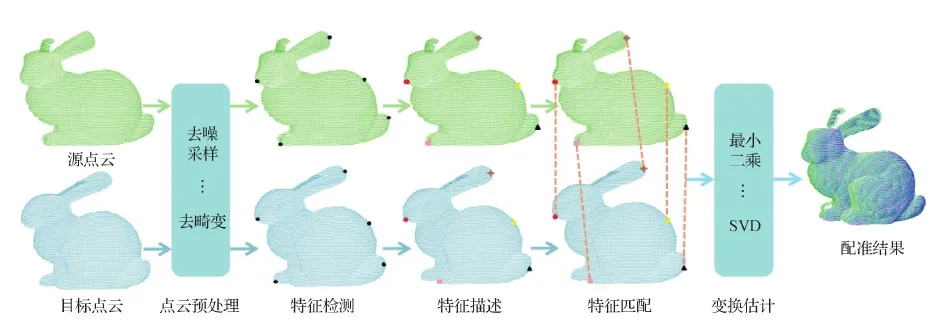
图1 典型的基于特征的点云配准方法流程Fig.1 Typical feature-based point cloud registration method process
配准方法与采集设备和采集方法有着较大的相关性,除了空间位置,一些点云采集设备还能提供其他信息。如一些激光雷达可以提供反射强度信息,RGBD(red, green, blue and depth)相机能够提供颜色信息,得益于这些增加的信息,为基于特征的点云配准方法提供了更多的思路和方向。如果点云只包含位置信息,那么对于其特征的描述最常用的是点特征、线特征和面特征。通过这些特征,大多数情况下能够完成配准任务,但是当物体对称性很强或者想提升配准的性能时,往往需要其他特征的辅助,纹理特征是主要的辅助特征的形式。在点云采集设备中,无论是反射强度还是颜色,都可以将其视为纹理特征,并且能够找到其与点的空间位置的对应关系,这是可以方便地使用纹理特征的基础。纹理特征可以用于确定特征对应关系,空间位置负责计算变换矩阵。
1.2.1 特征检测方法
对所有的点求描述符是不合适的,一方面这会极大地加重计算负担,另一方面这对配准也没有很大的帮助,因为点云中具有很多相似的点云部分,这会导致不必要的计算量,增加特征匹配数目和错误匹配概率。以信息论的观点,独特性不高的区域是信息量少的区域也是对点云配准帮助不大的区域。当然独特性也要考虑噪声、遮挡和离群值的影响,因为其产生的特征可能对配准没有帮助而且是有害的,所以使用特征检测获得尽可能保持点云主要特征的部分。衡量特征检测算法性能的重要指标是特征的可重复性和提取出特征的独特性。
点特征是一种最常用的点云特征。Masuda等人(1996)采用基础的随机采样法提取关键点,虽然这种方法很简单并且能有效控制点的数量,但是其没有办法确保采样的点均匀分布在点云上。Kamousi等人(2016)提出最远点采样法,解决了此问题。但是它们都无法确保选择到对配准有更大帮助的点,也无法保证两个点云中提取的关键点有更多相似的位置,即保证检测的可重复性。Rusinkiewicz和Levoy(2001)提出了法向空间采样方法(normal-space sampling),其想法是使法线在所选点之间的分布尽可能广泛,这样不会让所有的点都落在大平面上,在一些小却独特的区域也可以有比较大的机会选中。于是根据法线在角度空间中的位置对点进行存储,然后对按角度存储的点进行均匀采样,使各个方向法线都能取到。Zhong(2009)提出用一定半径内的协方差矩阵提取关键点,选择协方差矩阵特征值的最小值变化比较大的区域的点,这样提取的关键点更有可能是点云中的特殊点。Tian等人(2016)将Sipiran和Bustos(2011)提出的用于多边形网格的Harris 3D算法改进为更适合点云的变体。Harris 3D算法的核心思想在于计算Harris响应并选取在几何邻域中有Harris响应局部最大值的点作为关键点,其中Harris响应是对各个方向上的导数变化趋势的综合考量,能够表达点周围的形状,引入多尺度的概念,在多个尺度下计算Harris响应,选择几何邻域和尺度邻域中具有响应局部最大值的点作为关键点。Prakhya等人(2016)提出HoNO(histogram of normal orientations)方法,为每一个点计算法线和HoNO值作为判据,以去除平面区域并仅保留输入点云中的凹凸区域或其他信息丰富的区域。然后执行修剪步骤,即在一定范围内关键点应有最低的HoNO峰度值或该点具有最强的法线变化,满足条件即视为关键点,从而将显著区域减少到最终关键点集。
除了检测点特征,线特征作为一种可以有更大距离跨度的信息,也是一种很常用的特征。Stamos和Allen(2002)提出一种将点云先划分为平面块,然后得到平面之间的交线,取线到面边缘的距离小于一定阈值的线段作为特征。Yang等人(2016)提出一种具有语义的线性特征,首先将地面点云删除,然后对点云进行一层层的分割,提取点云中的极状点、交点和顶点,将其连接为3种类型的垂直特征线。Prokop等人(2020)首先通过协方差矩阵的特征值提取尖锐特征点,然后通过Hough变换提取其中的直线特征。Tao等人(2020)将3维点云投影到重力方向变成2维点云,通过密度约束获得高密度部分,然后执行区域生长算法得到线特征。Yang和Zang(2014)则提取曲线而不是直线信息,用点邻域的协方差矩阵的最小特征值分析点周围的几何曲率,将几何曲率大的点划分为若干线性簇,将线性簇拟合为波峰线作为特征。面特征具有更高的信息量并且对噪声更不敏感,虽然一些点特征考虑到其一定范围内的点云,相似于面特征,但是其考虑的面的范围有限。Brenner等人(2008)应用区域生长法,通过迭代种子区域选择和区域扩展两个步骤,得到平面特征。Chen等人(2020)用基于RANSAC的平面提取方法,得到平面特征。Xu等人(2019)将点云划分为体素,计算体素内点的曲率,将满足平面要求的平面块组合为平面特征。
得益于图像领域已有的研究,点云纹理特征的检测可以方便地借鉴其相关方法。Zhang等人(2019)将反射强度处理为2维图像,然后使用尺度不变特征变换(scale-invariant feature transform,SIFT)算法中的特征检测方法,本质上是以高斯函数差分(difference of Gaussian,DoG)的极值位置对应的空间点作为特征点。Wang等人(2016)不将反射强度处理为2维图像,而是直接使用一个3维高斯函数来卷积每个点云金字塔层次上的反射强度图像,相邻高斯平滑反射强度图像相减生成DoG 3D,取DoG 3D的极值作为检测到的特征。更多的纹理特征来自于点云的颜色信息,Liu等人(2007)在RGB表示的纹理图像中使用DoG方法,并剔除不稳定的局部峰值,获得关键点。Jung等人(2018)使用fast-Hessian detector检测关键点,功能类似于DoG,使用盒滤波器进行近似计算,检测速度有了很大提高。Ji等人(2013)使用FAST(from accelerated segment test)特征检测器,然后根据Harris测度对其进行排序,选取排在前面的点作为特征点。Yang等人(2020)使用超体素的方法,超体素考虑到了空间坐标、颜色值和局部几何特征,以超体素的中心作为检测到的特征点。
1.2.2 特征描述方法
检测到的特征有时并不适合直接用于特征匹配,因为点云是一种离散的、非结构化的数据,并且受噪声、遮挡和离群值的影响。如果将检测到的特征表述为描述符,通过描述符可以增加特征的鲁棒性,加快特征间的对比和匹配。对于相近的点云分布,其点云描述符应该也具有相似性,而对分布不相近的点云,其描述符应该也具有不一致性。描述符具有一定的压缩性,可以将复杂高维的点云特征压缩为更简单的表现形式。典型的描述符有特征签名和特征直方图。特征签名提供数值结果作为点的描述符,特征直方图方法则将点云信息表述为直方图。得到特征描述符之后就可以进行特征匹配并计算变换。
点特征的描述是点云特征描述中研究较多的方向。Feldmar 和Ayache(1996)提出用点附近计算出的主曲率作为描述符。主曲率表示关键点周围表面上的最大和最小曲率,并且综合关键点处的法线与最大和最小曲率对应的主方向作为该关键点的描述符。该描述符是刚性变换不变的,但是因为法线方向的歧义性,所以需要考虑法线可能的两个方向。Chua和Jarvis(1997)提出应用主成分分析(principal component analysis,PCA)提取特征,利用数据点3D坐标的加权协方差矩阵的3个特征向量,分析特征向量得到关键点,将主成分视为点描述符。Frome等人(2004)提出3D形状上下文描述符(3D shape context,3DSC),首先对整个点云进行随机采样得到N个点,确保选择的点尽可能在点云中均匀分布,然后建立每个点到其他N-1个点的向量,对空间进行球体划分,可以选择壳模型、扇形模型和混合模型,构建直方图描述符。但是这样的直方图描述符不是旋转不变的,所以需要执行标准化步骤,执行将质心作为原点的平移和对对象执行主轴变换,得到平移旋转不变性。Zhong(2009)提出固有形状签名(intrinsic shape signatures,ISS)描述符,使用从基本八面体递归计算的离散球形网格,均匀地划分球形表面,对邻域协方差矩阵进行特征值分解得到4个LRF(local reference frame),参照关键点处的LRF,使用其极坐标对每个邻居点进行编码。离散球面网格用于简化直方图。Rusu等人(2008)提出点特征直方图(point feature histograms,PFH),将关键点周围一定半径内所有的点全部互相连接,对其中的每一个点,寻找与另一个点构成的连线与该点的法线之间有最小夹角的点对,对所有这样的点对计算参考框架和角度之间的关系,对每个关键点,根据周围一定半径内每对点对的角度信息的值计算直方图描述符。点特征直方图(PFH)存在的问题在于其计算量比较大,是一个耗时的操作,于是Rusu等人(2009)提出一种改进的点特征直方图方法——快速点特征直方图(fast point feature histograms,FPFH),要构建快速点特征直方图,首先要计算简化点特征直方图(simplifified point feature histogram,SPFH),不同于点特征直方图考虑周围一定半径内所有点之间的关系,简化点特征直方图只考虑关键点和周围一定半径内点的关系,直接使用简化点特征直方图表示的信息量太少,所以将周围一定半径内点的SPFH加权为快速点特征直方图。
对于线特征的描述符,直线的描述较为容易,也较为常用。Stamos和Allen(2002)将线特征用五元组表示,即线特征编号、线起始点、线终端点、线所在平面的法线和线所在平面的大小,只需要源点云和目标点云间各一个这样的特征就可以估计变换矩阵。Yang等人(2016)使用九元组描述其语义线特征,包括构成线的最高点、最低点、点的数量、线的长度、线的序号、线的类型、线的半径和线支撑平面的两个方向。Tao等人(2020)将两个直线之间的夹角作为特征的描述,对直线方向的歧义问题,将所有线方向的反方向向量也纳入夹角的计算。对于面特征,也可以对其提取特征而加快特征匹配的速度。Brenner等人(2008)在提取面特征后,尝试了面积、周长和边界框的长宽比等后认为,这些特征不够可靠,可能会忽略正确的匹配,于是只保留法线和特征平面到原点的距离作为之后步骤的特征。Chen等人(2020)提取4个不平行的平面和2个平面的交线之间的关系作为特征,构成具有8个子特征的描述符,为了应对没有4个不平行的平面的情况,又提出减少1个平面要求的有6个子特征的描述符,只需一个这样的特征就能确定一个刚性变换。Xu等人(2019)从4个平面的法线与由法线组成的平面的交线之间的角度中构建不变特征。
对于纹理特征的描述,可以直接采用经典的图像特征的描述方法,一些研究将纹理特征和几何特征结合成新的特征描述符。Zhang等人(2019)直接使用SIFT特征描述方法描述由反射强度生成的强度图像特征。Liu等人(2007)使用SIFT特征描述方法描述RGB图像特征,通过2维图像到3维点云的映射,使描述符同时描述了3维特征点。Wang等人(2016)使用主成分分析确定特征的周围的包围盒,将其分为L×J×K个部分,将强度信息加权加入每个部分,作为该点的特征描述符。Jung等人(2018)使用成熟的SURF(speed up robust features)特征描述符描述检测到的特征。Ji等人(2013)使用ORB(oriented fast and rotated brief)特征描述方法,具体是使用BRIEF(binary robust independent elementary features)算法计算特征点的描述子,整体速度比SIFT和SURF更快。Yang等人(2020)使用三阶颜色矩,表示每个超体素的颜色分布特征,并与中心点的空间坐标相结合作为描述符。苏本跃等人(2019)将同态滤波后的最近8个点由拉普拉斯算子获得颜色特征,并与几何特征结合构成鲁棒的特征描述符。
1.2.3 特征匹配方法
特征匹配的过程也是一个变换估计的过程,获得关键点及关键点的描述符后,就可通过描述符之间的对应关系获得变换矩阵,有对应关系后配准问题就变成了凸问题,有很多方法可以得到变换矩阵,如SVD(singular value decomposition)、最小二乘法等。不同于类似ICP的过程,这里只需要获得一个粗配准的变换,因此在这里精度不是最重要的考量,对应关系健壮能够为接下来的精配准提供良好的初值。蛮力匹配方法是最基础的方法,假设两个点云都有n个特征,如果需要3个对应特征点以确定2个3D点集合之间的刚性变换,那么对应的3个点的数量就可能达到n6,其中只有一小部分可以确定正确的变换矩阵。这在点云中点的数量较少时是可行的,但是当点云数量很大时,这将是一个非常耗时的过程。有了特征提取和特征描述等信息就可以开发一些搜索策略,从而使特征匹配速度大幅加快,极大地降低计算成本。
随机抽样一致算法(RANSAC)通过反复选择数据中的一组子集来估计模型参数,将满足模型的数据称为局内点,不满足的称为局外点,选取局内点数满足要求的作为正确估计。将RANSAC思想用于特征匹配是一种经典的匹配方法。Chen等人(1999)详细介绍了一种RANSAC方法,并基于这样一个事实,即可以仅在两个点集中各取3个点来确定刚性变换。先在第1个点集上选择3个点组成目标三点集,为主点af、次点as和辅助点aa,相互之间的距离分别dfs、dsa和daf。然后在第2个点集上寻找与目标三点集形状相似的候选三点集。寻找候选三点集的具体步骤为:先任选一点bf作为与目标三点集第1个点对应的点,然后搜寻另一个点bs,其与bf的距离应近似为dfs,如果有这样的点则继续寻找点ba使其满足到bf的距离约为daf,到bs的距离约为dsa。重复这个过程,获得大量近似与目标三点集相似的候选三点集,每一个候选三点集都可以确定一个变换。通过验证点云中满足候选三点集确定的变换的点的数量,最佳的匹配使满足变换的点的数量最多,如此就得到了最佳变换矩阵。加入特征的约束,在选点时考虑特征是否相同,通过构建搜索树能够加快相同特征的搜索速度,并使找到的候选三点集的数量减少,减轻耗时的验证环节的负担。该算法具有鲁棒性,即使其计算效率不是很高,但是因为其简单性,可以用于各种特征,从而具有很好的通用性。RANSAC依然是一种应用较为广泛的特征匹配方法。
Gelfand等人(2005)提出用分支定界方法进行关键点的匹配,将坐标均方根误差验证转换为距离均方根误差,从而不需要计算变换矩阵就可以验证关键点匹配质量。该算法创建一个解决方案候选树,树中每个分支代表一个可能的点对应集合。当将一个可能的候选添加到解决方案中,如果这些可能的候选对象之一未通过阈值测试,并且距离均方根误差没有得到改善,那么就“修剪”掉这个对应集合的分支,通过探索整棵树最终找到最佳的对应。该方法也具有对噪声、遮挡和离群值的鲁棒性,但是对描述符的性能要求比较高。Theiler等人(2014)引入4PCS算法的思想,将关键点特征应用到4PCS算法,从而开发出K- 4PCS算法。在进行经典4PCS算法之前,首先计算关键点特征,将其用于4PCS可以加快相似共面四点集的搜寻速度,并且减少找到的相似共面四点集数量。Xu等人(2019)将平面作为K- 4PCS的特征,并设计了以角度而不是距离为度量的特征匹配方式。Ji等人(2017)将进化的方法直接用于角度变换空间的搜索,搜索最优角度变换。同样,进化的方法也可以用于关键点的匹配。Albarelli等人(2011)将博弈论框架用于关键点的匹配,自然选择过程允许满足相互刚性约束的匹配点得以幸存,从而消除了所有其他对应关系。收益矩阵(payoff matrix)代表对应关系,随着进化迭代,某种对应方式能够得到最多的支持,那么其就能够得到生存,最终的结果就是在一种变换下能够使最多的点产生正确的对应关系,也代表着最佳的变换方式。
上述方法适合于需要通过多对特征对应关系才能确定变换的条件下,对于一些线特征和面特征只需要更少的对应特征就能确定变换矩阵。Stamos和Allen(2002)设计的线特征两两之间就可以确定一个变换矩阵,通过阈值过滤线的长度和平面大小的比率不满足条件的特征,再通过阈值验证其他对是否匹配,迭代找到最佳匹配。Yang等人(2016)将得到的语义线特征组合为三角对,用结合线特征的三种约束获得相似的三角对,用几何一致性测试除去一些错误的对应,用剩下的对应计算变换矩阵。Tao等人(2020)使用两个直线构成的直线对的角度寻找匹配的直线对,以此确定一个不考虑重力方向上运动的变换,遍历寻找最佳对应关系。Brenner等人(2008)使用面特征构成三元组估计变换矩阵,但是在计算变换矩阵之前,先计算三元组的三重积,并按降序排序,因为三重积越大计算的平移误差就越小,并且当同一个变换出现预定次数时就停止迭代。Chen等人(2020)设计了面特征,只需要一对对应即可确定变换矩阵,通过建立kd-tree寻找近似特征,又通过kd-tree寻找相似变换,得到一些相似变换的均值,减少要验证的变换数量。
纹理特征的特征匹配方法与点特征的特征匹配方法有很多共通之处,因为较多的纹理特征和点特征一样属于局部特征。Zhang等人(2019)使用RANSAC确定正确的从反射强度图像中提取的特征的正确匹配关系。Wang等人(2016)使用CTNC(closest to next closest)技术,即对于每一个特征,与其最相似的和第二相似的特征满足一定的比例要求才认为其是正确的匹配特征。Liu等人(2007)在确定匹配关系时,引入对极几何的约束,基于RANSAC的思路,寻找使最多特征点满足对极几何的约束的特征匹配。为了应对RGBD相机的视点对SURF特征的影响,Jung等人(2018)利用3维点云生成不同视点的2维合成图像,再生成不同分辨率的缩放图像,这样产生大量重复的特征匹配关系,然后投票选择重复多的匹配关系作为最终的特征匹配。Yang等人(2020)使用权值权衡颜色特征和空间特征,并以此作为特征距离度量,当两点云的空间位置相差较大时,采用颜色特征比空间特征更准确,当点云大致对齐时,更适合利用空间特征匹配点云的几何细节。苏本跃等人(2019)使用迭代最近特征的方法,迭代估计特征匹配关系和变换矩阵。
表2总结了基于特征的点云配准方法中各种形式的特征的特征检测、特征描述和特征匹配的经典方法。
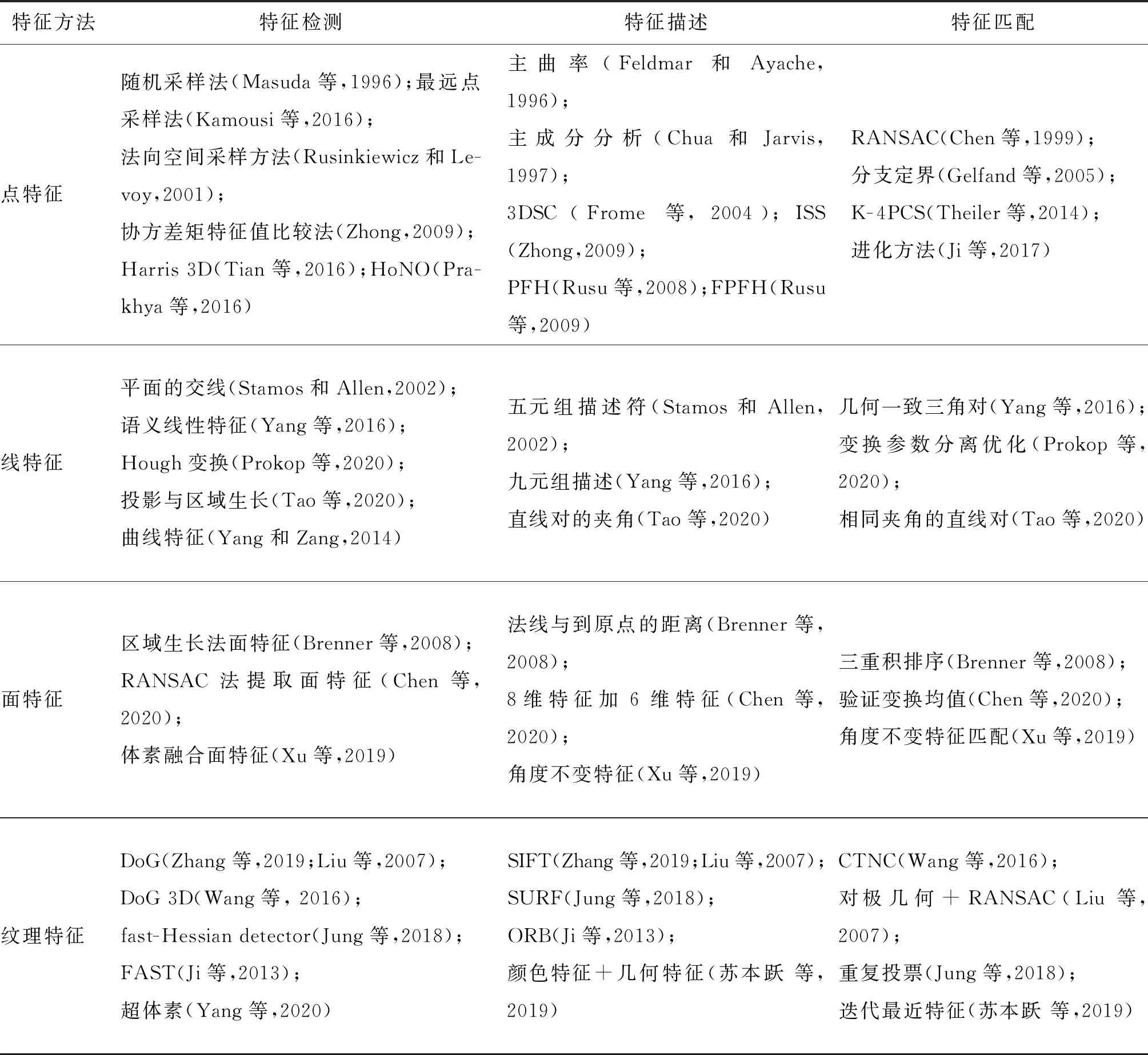
表2 基于特征的配准方法Table 2 Feature-based registration method
2 基于学习的点云配准方法
随着深度学习的发展,基于学习的点云配准方法得到广泛研究和深入发展。基于学习的方法对比非学习方法,最大优势在于相同配准性能下计算速度可以更快以及能学习到更高级的特征,从而达到更高的鲁棒性。基于学习的点云配准方法大量借鉴了非学习的点云配准方法的思想和深度学习方法在处理其他问题中的思想。根据配准方法的结构是完全由网络组成还是将非学习方法的一部分组件替换为基于学习的网络,将基于学习的点云配准方法分为部分学习的方法和端到端的学习方法。部分学习的方法优势在于灵活性,可以容易地用于其他点云任务如点云分类、分割和检测,也能够将其他任务中用到的网络直接用于点云的配准,这样比较简单的网络在一些应用中也更容易部署。而端到端的学习方法优势在于统一性,不用借助其他方法就能直接实现点云配准,准备训练的数据和评价训练的结果更加容易,也更有利于整体性能的提升。
2.1 在点云上学习的方法
将深度学习用于点云是一个具有挑战性的问题,因为点云是非结构化的,点之间的关系不是明确的,点的分布密度也可能各不相同。在点云上进行学习的方法分为3类,即基于体素的方法、基于多视图的方法和基于原始数据的方法。基于体素的方法将点云转换为结构化的3D体素结构,并将其与3D卷积核进行卷积,用类似图像深度学习的方法卷积、池化和连接层进行学习(Maturana和Scherer,2015;Meng等,2019;Zhou和Tuzel,2018)。尽管基于体素的方法表现出良好的性能,但由于大多数体素中都没有或者只有少量的点,这样的稀疏性会导致很高的无效内存消耗和计算量,从而导致无法将点云进行更加细致的体素划分。另一种方法基于多视图,将3维非结构化的点云通过在多个方向上的投影转换为2维结构化的图像的集合,然后对其用图像深度学习方法处理并整合(Qi等,2016;Su等,2015;Kanezaki等,2018)。不同于基于体素的方法,基于多视图的方法可以进行更加细致的划分,数据量不会太大即可包含丰富的纹理信息。多视图方法的限制在于视点的选择和不同视点的整合比较困难。在点云上学习目前最流行、应用最广泛的方法是基于原始数据的方法。其中,PointNet是最为经典的一种基于原始数据的点云学习方法(Charles等,2017)。为了能够直接在点云上进行学习,引入可学习参数并且参数由每一层中的所有点共享的多层感知器(muti-layer perception,MLP)和为了使其输出与输入顺序无关的对称函数。在PointNet中,MLP层将点特征从3维转换为1 024维,将maxpooling函数作为对称函数,获得与输入顺序无关的全局1 024维特征。PointNet取得了很好的性能,结构图如图2所示。但是PointNet得到的是一个全局特征,而无法捕获本地特征,一些情况下其鲁棒性会下降。为此,研究者提出了许多能够捕获本地特征的方法。
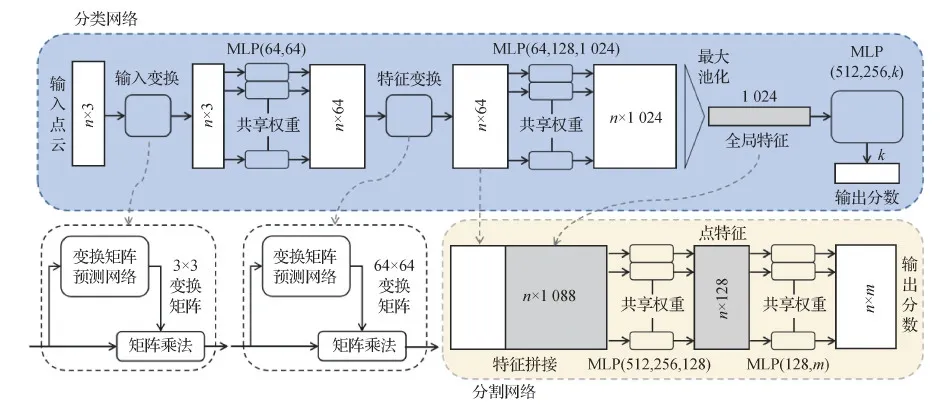
图2 PointNet结构图(Charles等,2017)Fig.2 PointNet architecture(Charles et al.,2017)
Qi等人(2017)扩展了PointNet,提出了PointNet++,在局部区域分层应用PointNet,以适应性地组合来自多个尺度的特征,提供了本地特征。Wang等人(2019)提出DGCNN(dynamic graph convolutional nerual network),使用 EdgeConv网络模块提取点云局部邻域的特征,可以通过堆叠EdgeConv模块获得更高层次的特征,所以能够提取到表示很大范围的特征,取得了很好的效果。
2.2 部分学习的点云配准方法
最初利用深度学习解决点云配准问题的尝试使用了部分学习的点云配准方法,该方法直接用基于学习的组件替换掉非学习点云配准方法中的某个组件,这就可能给原来的算法带来速度或鲁棒性的提升。部分学习的点云配准方法最大的优势在于灵活性,能够与其他方法组合,也可以直接用于其他领域。
Zaganidis等人(2018)提出语义辅助正态分布变换(semantic-assisted normal distributions transform,SE-NDT),应用PointNet提供全局特征,并与局部特征由分割网络连接。分割网络输出该点的类别,从而提供分类语义信息,将其用于NDT算法取得了很好的性能,另外将这种语义辅助信息用在GICP中则得到SE-GICP(semantic-assisted generalized iterative closest point)。Truong等人(2019)也实现了类似的基于语义分割算法的点云配准。
在关键点检测上,Li和Lee(2019)提出一种基于学习的关键点检测算法——USIP(unsupervised stable interest point)深度学习检测算法,使用特征提议网络(feature proposal network)获取原始点云以及对原始点云进行任意变换后点云的关键点,利用两种损失,即使两组关键点间的距离应尽可能小的probabilistic chamfer loss和使提取的关键点尽量靠近实际点云的point-to-point loss,借此获得检测高度可重复且精确定位的关键点的能力。Du等人(2019)提出一种可同时学习关键点检测和特征描述的深度学习算法,以点云及其相对变换矩阵作为输入,输出候选关键点的位置、候选关键点的可能性以及候选关键点的特征描述。通过最小化对应关键点的距离和最大化不对应关键点的距离以及最大化对应关键点的可能性进行学习。
多数的部分学习的点云配准方法是基于特征的,而其中大多数的工作都集中于关键点描述上。Zeng等人(2017)提出一种基于体素上学习关键点描述符的网络,将关键点周围划分为体素并将其输入ConvNet网络,学习的目标是对应关键点的描述符之间的距离应最小化,同时拉开不对应关键点之间的距离。该方法使用随机关键点选择和RANSAC关键点匹配方法,构成完整的点云配准方法,达到了比较好的性能。Elbaz等人(2017)利用学习的自动编码器进行描述符编码。首先用随机球面覆盖集(random sphere cover set)获得超点集,然后为其确定坐标系,再将其投影为2D图像,进行过滤和显著性检测操作后输入深度自动编码器,以原始图像和解码后图像间的像素差别作为损失。获得描述符后,用RANSAC方法进行点云配准,然后使用ICP算法进行精配准。Deng等人(2018b)提出一种特征提取与特征描述学习网络PPFNET(point pair feature network),输入从点云中均匀采样的N个局部点云,使用N个共享权重的PointNet获得各自特征,将这些局部特征通过最大池化层聚合为一个全局特征后加到每个局部特征中,再通过N个MLP处理得到最终的局部描述符。为了进行训练,通过参考真值计算N个局部点云的距离矩阵再二值化为对应矩阵,并构建训练得到的特征之间的距离构成的特征距离矩阵,利用两个矩阵计算N-tuple loss并优化网络参数,通过RANSAC与特征提取和描述功能综合为点云配准框架。PPF-FoldNet(point pair feature folding network)(Deng等, 2018a)进一步扩展了该算法。Yew和Lee(2018)提出3DFeat-Net学习特征的提取和描述,使用包含锚点和正负点的三元组训练网络,使锚点与正点的描述符更接近,与负点的描述符更远离。为此作者设计了由3个并行的共享权重子网络组成的学习网络,点云经过聚类后经检测(detector)模块学习权重和朝向,并在第1阶段选择权重大的点作为关键点,在下一阶段描述符网络仅为这些关键点计算描述符。分别对比锚点和正点、锚点和负点的特征,选择对应特征并用权重加权获得损失函数,用其与RANSAC结合成完整的点云配准框架测试其性能。Khoury等人(2017)也应用三元组训练描述符,得到了CGF(compact geometric features)特征。
2.3 端到端的点云配准方法
目前,很多工作都致力于端到端的点云配准的方法,从点云的输入到最后的配准结果都在一个完整的网络中实现,端到端的点云配准方法能够最大程度地发挥深度学习方法的高效和智能,也能够更好地发挥GPU的并行计算能力,有更快的速度。在深度学习网络中,能够反向传播是非常重要的,所以在构建端到端的点云配准网络时,要保证可求导,这样才能进行学习,而很多非学习方法中的组件是不可求导的,所以要对其加以改进。端到端的点云学习方式在训练数据上也比训练关键点检测器和关键点描述器容易,因为其通过配准的好坏进行评价,而关键点检测器和关键点描述器的评价相对困难。
Aoki等人(2019)提出PointNetLK算法,源点云和目标点云首先分别通过没有T-Net的PointNet网络获得全局特征,然后通过LK(Lucas and Kanade)算法估计对齐方式。点云配准要找到一个最佳变化矩阵,因此需要求损失对于变换矩阵的导数,为了方便计算将其转换为对李代数的求导。借鉴IC(inverse compositional)方法,使雅可比计算只需执行一次,大幅提高了效率,训练目标为网络输出的变换矩阵的逆矩阵与变换矩阵真值的矩阵相乘结果应尽量接近单位阵。Yuan等人(2021)将经过聚类和3DFeatNet特征描述层后的特征馈入一个全连接层,所有特征之间两两计算权重,使用SVD方法获得最终变换矩阵,训练目标与PointNetLK相同。Kurobe等人(2020)使用PointNet获得特征,然后再将源点云全局特征和目标点云全局特征与局部特征结合,通过MLP获得对应关系,使用SVD获得最终变换参数。Huang等人(2020)提出一种网络,在不需要搜索对应关系的情况下,通过最小化特征空间上的投影误差解决配准问题,并且保持了配准的过程性。Lu等人(2019)提出DeepVCP(deep virtual corresponding points)算法,使用PointNet++提取特征,通过点云加权层学习每一个点的显著性,以避免动态物体干扰,点云特征嵌入DFE(deep feature embedding)层为关键点提取更加精细的局部邻域特征,通过初始位姿得到预测对应点并将其周围体素化划分,从中选择更好的对应点。ICP算法选择最接近的点作为对应点,导致不能求导而无法反向传播,对此提出对应点生成CPG(corresponding point generation)层得到对应点,并通过SVD再计算对应点引入关键点之间的统一的几何约束,是一种基于学习的精配准方法。Wang和Solomon(2019)提出deep closest point算法,借鉴ICP思想,首先经过DGCNN学习特征,接着transformer组件使两点云特征具有来自两个点云的上下文信息,pointer层避免选择不可微分的特征对应硬分配而是权重对应,最后使用SVD分解获得变换。Yew和Lee(2020)提出RPM-Net(robust point matching network),使用PPF(point pair features)作为特征提取模块的输入,使用具有确定性退火调度的软分配方案,以在每次迭代时逐渐“强化”分配,使用网络学习预测最佳退火参数α、β,通过特征和参数α、β获得匹配矩阵,从而估计特征对应关系,使用SVD计算变换参数。RPM-Net的特点是可以迭代执行配准并收敛。
表3总结了典型的基于学习的点云配准方法的典型方法及其特点。
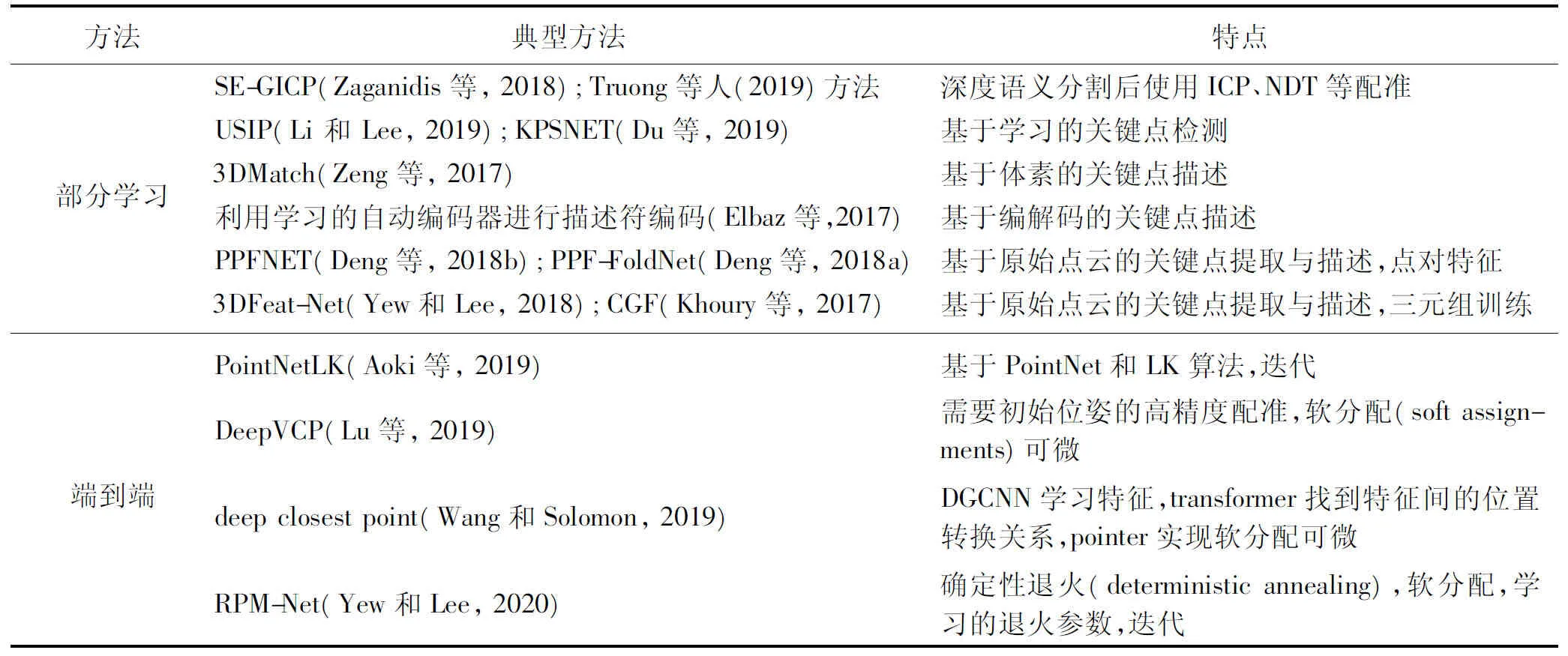
表3 基于学习的点云配准方法Table 3 Point cloud registration method based on learning
3 结 语
本文将点云配准方法总结为非学习的方法和基于学习的方法,介绍了经典方法、基于特征的非学习方法、部分学习的方法和端到端学习的方法,分析了一些算法的细节和同类算法的特点。很多经典方法及其变体都属于精配准方法,精配准方法有着比较快的配准速度,常常作为粗配准后的优化方法。基于特征的非学习和基于学习的方法则常常作为粗配准用来提供良好的初始位姿,虽然各种方法差别很大,但是特征往往在其中起到最重要的作用。基于学习的方法成为目前比较热门的研究方向,对比非学习的方法,其相关的论文发表量具有更高的增速,但是非学习的方法的文献还是要比基于学习的方法的文献多。目前两类方法都还有很多可研究内容,并有希望取得进一步的突破。
点云配准技术经过多年发展,已经取得了很多成果,并且随着点云配准技术的发展和深入到生产生活中,更多应用对点云配准技术提出了更高的挑战。主要挑战有:1)应用场景的挑战。如大规模的点云、动态非稳定的点云、缺乏特征、重复特征或对称的点云,这些应用场景对点云配准的可用性和可靠性提出了很高的要求。2)配准性能的挑战。如要能满足一些应用中高精度的要求,在实时应用中需要保证快速配准,达到更高的配准准确率、更高的配准精度配准速度比和更高的配准精度计算负担比。3)应用条件的挑战。在计算资源有限的设备上能否达到可以接受的配准效率,在点云只是部分重叠时能否配准成功。4)算法的通用性问题。现有的点云配准方法能够应对一些挑战,但是现有的点云配准方法仍存在一些缺陷和不足,如很多精配准方法虽然能达到好的配准精度,但是需要一个良好的初始位姿,否则容易陷入局部最优。一些粗配准方法不需要初始条件,但是需要更多的计算以找到全局配准参数,并且配准的精度往往不高,需要结合精配准以提高其精度。基于学习的方法仍主要集中于简单物体的配准上,对于复杂场景、大规模点云上的研究还不是很多,还缺乏在这些场景下的基准数据集。高准确率高精度往往意味着高的时间消耗和大的计算负担,能达到二者都很优秀的配准方法不多。
为了应对点云配准面临的挑战,提高点云配准算法的性能和实用性,展望点云配准算法未来的发展趋势,可能会有以下特点:1)更多地运用点云和特征的高效存储与索引方法,能够消除部分信息冗余的点云预处理与特征表示方法,高效的特征匹配方法和优化方法等能够减少时间消耗的策略;2)可以采用由全局到局部、由粗到精、多尺度的渐进优化方法,混合各种方法的特点,融合构造新方法;3)寻求更加具有代表性且数量较少、提取更方便快速、更加鲁棒和受离群值、噪声、采集条件影响更小的特征,提取全局特征,从更大范围提取局部特征和语义特征;4)对特定的应用环境,构造特定的方法,针对性的设计应对策略;5)运用深度学习的方法,构建更加符合应用需求的基准数据集、创新的配准网络或借鉴其他深度学习任务的思路方法,发挥深度学习在深层次特征、语义提取、理解与辨识和应对复杂场景的能力;6)无监督自主地进行点云配准,能够检测配准失败,并自动纠错或进行其他处理;7)适应并应用新的点云采集设备和使用其他辅助设备,使用新增的信息,融合增进效果。

