有限元方法教学探析

苏海燕

（新疆大学 数学与系统科学学院，新疆乌鲁木齐 830046）

在物理学、化学、生物学和数学等领域中，许多现象和规律通常可以用偏微分方程来揭示。然而，在一般情况下，绝大多数的偏微分方程初边值问题无法给出解析解，采用有限元方法进行数值求解该类方程是当前主流的研究手段之一[1]。有限元课程的教学内容主要包括理论分析和数值模拟两方面。在数值模拟方面，虽然现在已经有很多有限元数值模拟软件 （如FreeFEM++, Fenics, COMSOL 等）仅仅利用偏微分方程所对应的变分形式，就可以通过几行代码非常便捷地得到数值解，但是这不利于初学者领悟有限元方法的核心和本质。

本文主要结合笔者的学习以及多年的有限元方法教学经验，旨在通过引入方法，详细地介绍有限元方法的主要思想，引导学生循序渐进地学习有限元方法的理论基础和数值编程。

1 有限元方法

下面我们将详细介绍有限元方法求解偏微分方程的主要步骤及其易于拓展到高维数和复杂问题的编程思想。

1.1 确定问题

本文考虑如下的椭圆形方程[2]：

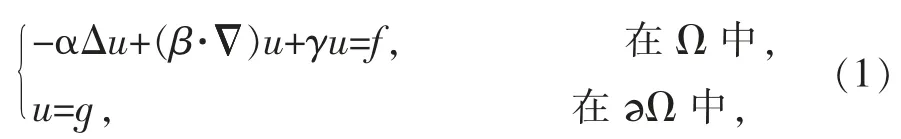
1.2 变分格式

众所周知，变分原理是有限元方法的基础[3]，因此我们将首先推导(1)式的变分格式。 令

对（1）式左右两端同时乘检验函数v，然后采用分部积分，则可得如下变分问题：

1.3 网格剖分

针对二维问题，网格剖分可分为三角形网格剖分、四边形网格剖分、多边形网格剖分等。采用不同的网格剖分方式，将直接影响下一节中基函数的建立。本文将采用最常见的三角形结构网格进行讨论[4]。

1.4 基函数

由于方程(4)是无限维空间中的问题，有限元方法要求用有限维空间逼近无限维空间，在有限维空间中对原问题进行逼近[5]。 接下来介绍有限元空间的构造，假设

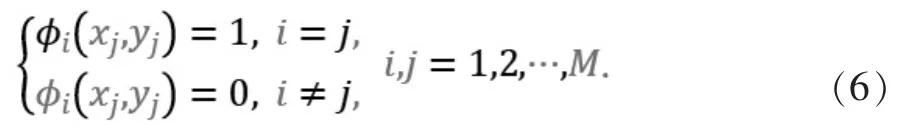
常见的多项式基函数有一次多项式基函数、 二次多项式基函数等。 在本文中，我们采用P1有限元，即基函数Φ 在每一片上是线性多项式Φ=ax+by+c，其中a，b，c 是常数。

1.5 离散格式

接下来，在上述建立的离散有限元空间中对连续变分格式（4）进行有限元离散[3]。 对，有

则可得离散格式，如下：

vh的任意性，取vh=Φj，j=1，2…，M，则有

综上所述，问题（8）可以转化为以下形式：

1.6 数值积分

由上一节的推导，可以发现(3)式是计算矩阵A，B，C，F 的基础。 因此，如何快速、高精度地计算(3)式显得尤为的重要。 接下来，这里简单回顾一维高斯积分、二维正方形高斯积分和二维三角形高斯积分[6]。

若函数f（x）∈C2n[-1，1]，则使用高斯-勒让德求积公式：

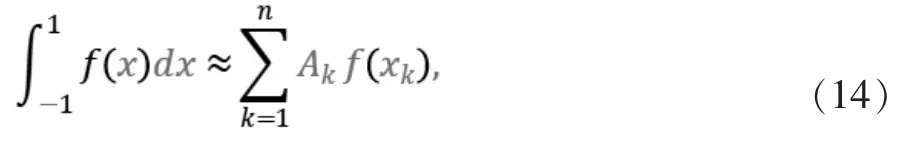
其中xk为高斯点，即是n 次勒让德多项式Pn（x）的零点，An是求积系数：

若函数（x，y）∈C2n，2n[-1，1]2，则采用如下积分公式：

其中xi，xj分别是x，y 方向的高斯点，Ai，Aj为相应的求积系数。

若函数定义在单位三角形上时，需将积分进行坐标变换到正方形区域后利用(16)式进行计算：

其中

xi，xj分别是x，y 方向的高斯点，Ai，Aj为相应的求积系数。

1.7 组装矩阵

在计算机编程实现中，数值计算矩阵A，B，C，F 通常有两种思路： 第一种是对矩阵中的每个元素逐一进行计算，然后组装为最后的总矩阵。第二种是对网格剖分中的每个单元进行矩阵的计算，最后进行组装[7]。 此外，根据基函数的定义，我们可以发现在计算

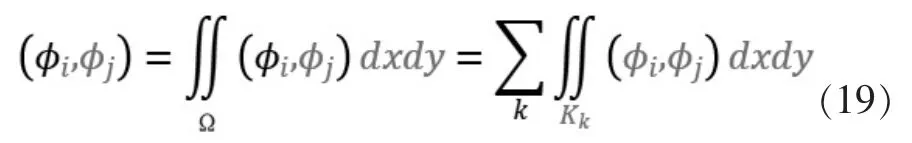
的过程中，当Φi，Φj的非零函数区域不相交时有

因此，局部矩阵是稀疏的，为了节约计算储存空间，我们在实际计算中利用小矩阵或者稀疏矩阵进行存储，并记录局部矩阵在总刚矩阵中的位置，为准确的总刚度矩阵合并提供保障。 另外矩阵AC 是对称矩阵，所以可以通过矩阵的对称性初步验证矩阵组装的正确性。 经过上述分块组装后，进行最后的合并：

1.8 边界处理

在本文中，我们考虑第一类边界条件，因此仅需对上一节中组装好的总刚矩阵L 进行边界处理。 需要将边界节点i 所对应的行替换为0，再令对角元Iii=1，如：假设i 为边界点，则进行如下处理：

此外，若边界条件是第二类边界条件时，在推导变分格式的过程中会有新的矩阵出现，然后将其新产生的矩阵组合在L，F 中即可，而不需要进行类似(22)式的处理过程。

1.9 求解Lx=b

经过之前的一系列处理，我们即将得到偏微分方程的数值解。接下来，对Lx=b 进行数值求解。针对矩阵的不同性质，采用不同的求解器。 本文旨在让学生了解，采用有限元方法求解偏微分方程的具体步骤。 因此，直接调用程序库中的一些求解器进行求解。常见的求解办法有：Gauss 消去法，LU 分解法，Cholesky 分解法，迭代法，超松弛迭代法，共轭梯度法等[9]。

1.10 评估数值结果

虽然有了数值解，但我们对数值结果的优劣还未知。因此我们需要构造精确解算例，通过计算数值解的数值误差来评估数值解的精确度。通常情况下，我们会计算如下三种误差范数，以及结合网格参数计算收敛阶，以此判断数值解的准确性。

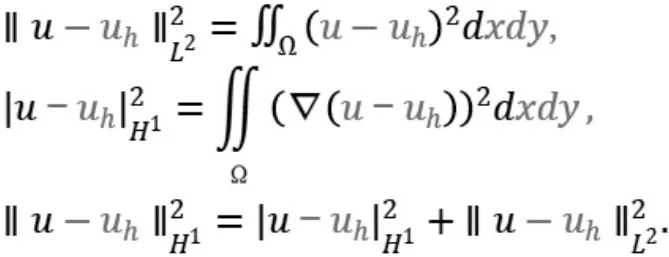
以及收敛阶计算公式，

其中Ei，Ei+1 是对应于网格参数为hi，hi+1 时的误差。 由文献[10]可知当采用P1 元时，||u-uh||2L2≤C h2，|u-uh|H21≤C h 和||u-uh||H21C h，其中C 是给定的常数。

接下来，我们构造一个真解uexact=x（x-1）y（y-1），则f=x2y2+x2y+x2+xy2-3xy-x+y2-y。 我们对方程(1)进行有限元计算，结果如表1所示。

表1 有限元数值误差结果及收敛阶

由文献[10]给出的误差分析可知，我们的计算结果(见表1)符合理论分析。

2 结语

本文结合笔者的学习和教学经历，对有限元方法的学习和教学过程进行了总结归纳。 以一个确定的偏微分方程，对如何设计编程实现有限元求解的每一个步骤进行了循序渐进的介绍。 虽然在编程上较为耗时且困难，但这个最经典的算法是大多数算法的基础，需要初学者扎实掌握。