舰船辐射噪声广义多尺度数学形态学特征提取与应用研究

郭 政， 赵 梅， 胡长青， 倪俊帅

(1. 中国科学院 声学研究所东海研究站，上海 201815； 2. 中国科学院大学，北京 100049)

当前水声目标识别技术的发展过程中，目标舰船识别一直是重点研究方向。舰船辐射噪声中包含了目标舰船的航行状态、自体振动及船体与水体相互作用等物理规律，因此有效提取表征这种物理规律的舰船辐射噪声特征参数成为了值得研究的问题。

舰船辐射噪声信号是一种非线性、非平稳的时变信号，因而线性方法在舰船辐射噪声特征提取中存在一定局限性[1-2]。近年来许多学者讨论了包括Lyapunov指数、关联维数、分形特征、样本熵等在内的非线性特征在舰船辐射噪声特征提取中的应用，取得了一定成果。

章新华等[3]研究了舰船辐射噪声的混沌特性，尝试提取了舰船辐射噪声的Lyapunov指数和分形维数。陈向东等[4]以相空间重构理论为基础讨论了舰船辐射噪声的非线性，验证了非线性方法应用于舰船辐射噪声特征提取的可行性。刘朝晖等[5]提取了水声目标分形特征向量并应用于水声目标识别中。焦义民等[6]在构造了非线性频谱字典的基础上提出非线性谱特征，较好地反映了舰船辐射噪声的低频特征。李余兴等[7]在集合经验模态分解(ensemble empirical mode decomposition，EEMD)基础上提取了舰船辐射噪声的样本熵。陈哲等提取了舰船辐射噪声的多尺度排列熵，在多个尺度上描述了舰船辐射噪声的复杂度特征。通过不同方法提取的舰船辐射噪声非线性特征参数从各个方面反映了舰船辐射噪声非线性、非平稳的特性，在不同舰船目标之间有良好的区分度。但多数非线性特征计算仍较为复杂，因此有必要进行方法改进，在保证提取的特征参数稳定性的基础上简化运算，采用更简洁的方法提取舰船辐射噪声的非线性特征，以减少计算所需时长。

数学形态学方法是一种非线性信号处理方法，其核心思想为利用各种形态特征不同的结构元素提取目标信号或进行信号降噪，能在分离背景噪声的同时将成分复杂信号分解为若干具有物理意义的部分[8-9]，以实现目标信号提取及后续处理；且数学形态学本质上仅涉及加、减、取极值等运算，计算简单，易于实现，因而在图像处理、机械故障诊断以及模式识别等领域已有广泛应用[10-13]。舰船辐射噪声信号作为一种非线性的一维时变信号，包含产生机理相异的构成成分，与数学形态学方法有较高契合度。本文将物理意义明晰且计算简单数学形态学方法应用于舰船辐射噪声的非线性特征提取，与熵的概念结合并加以改进，给出新的非线性特征计算方法。

本文在讨论数学形态学基本思想及数学形态谱计算方法的基础上，以腐蚀运算替代开运算，简化了多尺度数学形态谱计算过程，并借鉴多尺度熵(multi-scale entropy，MSE)的计算方法提出了一种广义多尺度数学形态腐蚀谱熵(generalized multiscale pattern erosion spectrum entropy，GMPESE)计算方法，进而应用于实测舰船辐射噪声，进行目标识别验证。目标识别结果证明了该方法的可行性。

1 数学形态谱基础理论

1.1 一维数学形态学运算[14]

一维形态学的基本运算包括腐蚀、膨胀、开运算和闭运算四种。假设f(n)和g(m)两离散信号的定义域分别为：F= (0,1,…,N-1) 和G=(0,1,…,M-1)，且M≤N。定义g(m)为结构元素，则f(n)关于结构元素g(m)的腐蚀运算定义为

(fΘg)(n)=min[f(n+m)-g(m)]

(1)

膨胀运算定义为

(f⊕g)(n)=max[f(n-m)+g(n)]

(2)

在此基础上，f(n)关于g(m)的开运算定义为

f∘g=(fΘg⊕g)(n)

(3)

闭运算定义为

f·g=(f⊕gΘg)(n)

(4)

在一维形态学运算中，结构元素g起到一种辅助滤波的作用，即通过与原信号进行简单的加减和求极值运算对一维信号进行滤波和信息提取。对于单位结构元素g，可定义λg为尺度λ下的多尺度结构元素。多尺度运算结构元素可以表示为

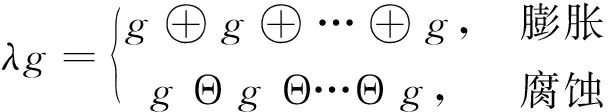
(5)

式中，共进行λ次腐蚀或膨胀运算。

1.2 多尺度数学形态谱

若f(n)为一维时间序列函数，g(m)为实值函数，则f(n)的数学形态谱可由式(6)计算

(6)

式中：A(f)为一维函数f在定义域内的面积； 当λ≥0时，SPS为开运算形态谱；当λ<0时，SPS为闭运算形态谱，λ的正负区间分别为信号本身的结构信息与背景信息，而两者具有一致性，因此通常对形态谱正区间即开运算形态谱进行研究。与频谱、功率谱等谱函数能够描述信号在不同频率上的成分类似，数学形态谱也可以从多个结构元素尺度上对信号进行描述。对于一维离散信号，给定信号一维离散化定义区间λ∈[0,+∞)，式(6)可简化如式(7)所示

SPS(f,λ,g)=A[f∘λg-f∘(λ+1)g],λ≥0

(7)

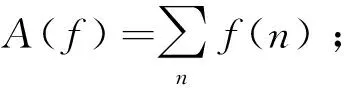
2 数学形态腐蚀谱及广义多尺度数学形态腐蚀谱熵特征计算方法

2.1 改进的数学形态谱——数学形态腐蚀谱

基于形态谱的特征提方法取在故障诊断等领域已有较多应用，且表现良好。但传统形态谱方法应用于舰船辐射噪声特征提取时，对不同的目标舰船区分度并不理想。对传统形态谱进行改进，以腐蚀运算代替式(6)中的开运算，定义数学形态腐蚀谱(pattern erosion spectrum，PES)为

(8)

与前述过程相似，式(8)的一维离散简化为

SPES(f,λ,g)=A[fΘλg-fΘ (λ+1)g],λ≥0

(9)

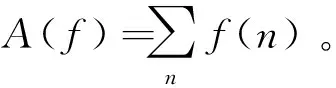
2.2 广义多尺度数学形态腐蚀谱熵计算

自Shannon提出信息熵的概念描述信息的不确定性以来，以信息熵为基础逐步发展出了K-S熵、近似熵、模糊熵、样本熵和排列熵等反映信号复杂度和不确定性的熵值计算方法。

根据事件λ出现的概率q(λ)，可以计算信息熵

(10)

由于数学形态谱可在若干个结构元素尺度上描述信号，能较好的契合“某一事件出现的概率”这一概念，因此可以引入信息熵，应用数学形态学方法计算信号熵值EPESE

(11)

式中，EPESE为数学形态腐蚀谱熵(pattern erosion spectrum entropy，PESE)，q(λ)=SPS(f,λ,g)/∑SPS(f,λ,g)。

改进后的数学形态腐蚀谱熵与传统数学形态谱熵在尺度上特性相似，即可以从多个结构元素尺度上分析评估信号，但仅在单一时间尺度上描述信号的非线性特性，未能从更全面的时间尺度分析信号的固有特性。这一点与样本熵的局限性类似。为此，借鉴Costa等[15-16]提出的MSE计算方法，在多个时间尺度上衡量信号的非线性与复杂性特性，并将所考量的多时间尺度推广到多时间尺度及多结构元素尺度，给出一种广义多尺度数学形态腐蚀谱熵的计算步骤：

步骤1选取待处理舰船辐射噪声信号x(i)，其粗粒化时间序列y(τ)可表示为

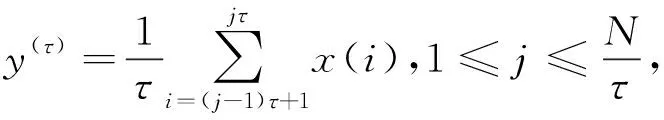
(12)

此时，粗粒化过程相当于按矩阵Y进行相空间重构

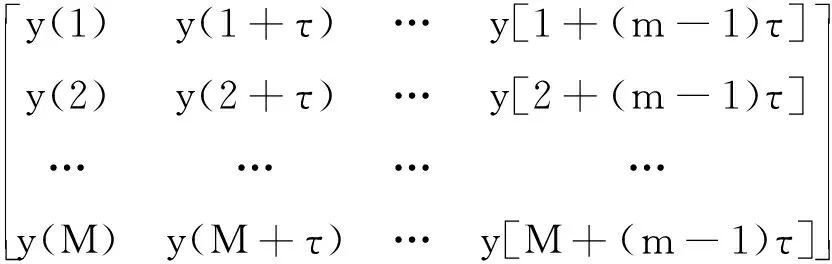
(13)

式中，M=N-(m-1)τ，m为嵌入维数，τ为时间尺度因子。对应时间尺度因子τ=1,2,…,τmax计算得到的时间序列长度为floor(N/τ)，floor为向下取整。因此当τ=1时，时间序列为原时间序列。

步骤2根据式(11)计算各粗粒化时间序列的形态学腐蚀谱熵值EPESE，并将其组合为粗粒化时间尺度因子的函数，得到广义多尺度数学形态腐蚀谱熵

EGMPESE(x,λ,τ)=EPESE(y(τ),λ,τ)

(14)

3 舰船辐射噪声试验及实测数据概况

为验证GMPESE特征提取方法在不同信道和环境噪声条件下进行目标舰船辐射噪声特征提取可行性，本文选取中国科学院声学研究所东海研究站于2018年6月千岛湖试验及2020年1月东海试验中采集的舰船辐射数据进行处理。

两次试验中设备布放与环境情况均有所不同。

(1) 千岛湖试验中试验地点水深为64 m。试验以潜标方式进行水听器布放，水听器工作带宽为1 Hz～12 kHz，采样频率为32 kHz。两个自容式水听器及两个TD分别对应固定在潜标上，入水后位于9.3 m与31.4 m深处，如图1(a)所示。由TD数据估计得到千岛湖试验水域声速剖面，如图1(b)所示，为典型千岛湖夏季声速剖面。

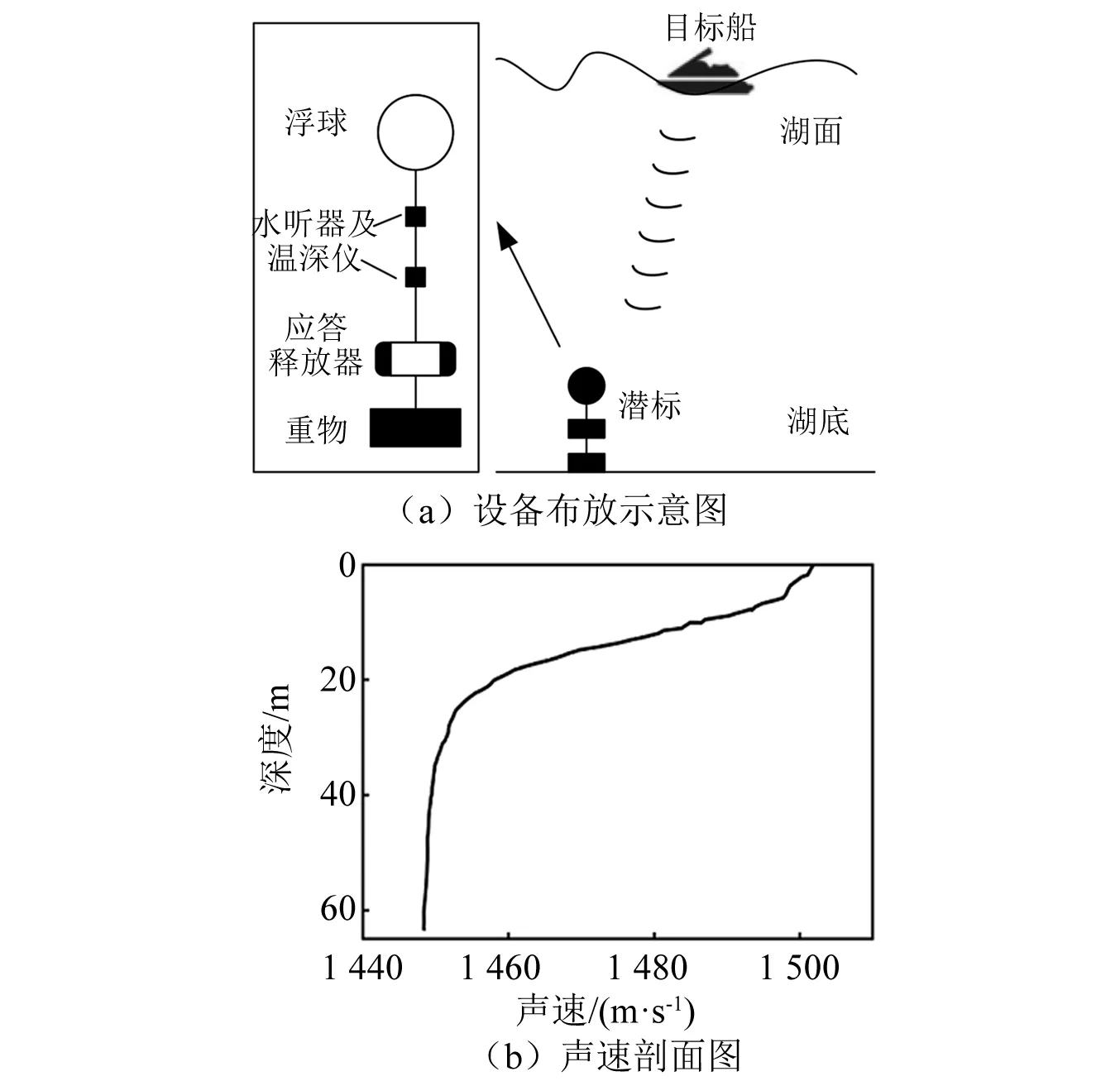
图1 千岛湖试验设备布放及试验水域声速剖面Fig.1 Equipment deployment and sound velocity profile of Qiandao Lake experiment

(2) 东海试验中试验地点水深为38 m。试验采用钢质硬连接方式布置了工作带宽为20 Hz～20 kHz，采样频率为48 kHz的八元水听器水平阵列，水听器接收阵列固定在浮标上，如图2(a)所示。水平阵两端安装有温深仪，入水后位于8 m深处。此外，由于当日风速较大，水流较急，试验选择以关闭主机并抛锚的试验船牵引浮标的方式，保证水听器阵列不产生大范围漂移。试验海域声速剖面由CTD测得，如图2(b)所示，为典型东海浅海的冬季声速剖面。

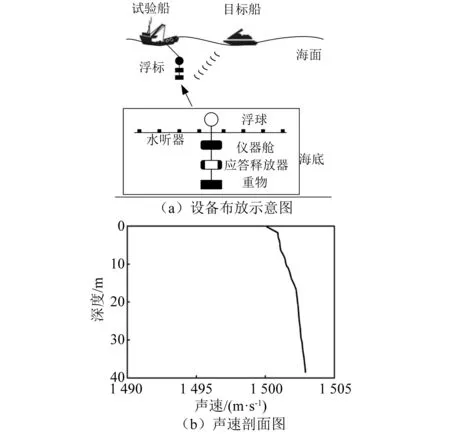
图2 东海试验设备布放及试验水域声速剖面Fig.2 Equipment deployment and sound velocity profile of East China Sea experiment

两次试验于不同季节进行。由图2可知，其声速剖面分别为正、负梯度，涵盖了典型的冬、夏两个季节的浅海(湖)声信道情况。

选取千岛湖试验中获取的Q1～Q4船的舰船辐射噪声数据及东海试验中获取的D1～D5船的舰船辐射噪声数据，用于后续分析及舰船目标识别验证。Q1～Q4及D1～D5舰船辐射噪声时域波形，如图3所示。

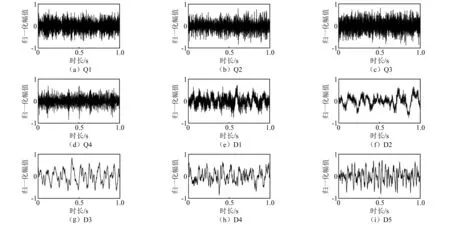
图3 实测舰船辐射噪声时域波形Fig.3 Time-domain waveform of measured ship radiated noise

下文中，首先以东海试验数据为例进行GMPESE相关参数及影响因素的分析，然后综合考虑千岛湖试验数据和东海试验数据，分析对比不同目标舰船之间GMPESE特征及MSE特征的区分度，并进行目标识别验证。

4 参数选取影响分析

在数学形态学方法应用中，结构元素的种类与其参数选取是一个重要问题。目前常见的结构元素包括扁平结构元素、三角结构元素、半圆结构元素、正弦结构元素等。为保证信号形状在运算过程中相对稳定，通常选取与原信号形状接近的结构元素进行数学形态学运算。

对同一信号分别应用扁平结构元素、三角结构元素及半圆结构元素的数学形态学运算，结果如图4所示。由图4(c)可知，因半圆结构元素与信号形状差异较大，进行多次数学形态学运算后难以保持信号原有形状；由图4(a)和图4(b)可知，因三角结构元素及扁平结构元素与信号形状差异较小，进行多次数学形态学运算后较好地保持了信号原有形状，两者相比半圆结构元素更适合于一维信号数学形态学运算，且应用扁平结构元素进行数学形态学运算时信号幅值不会产生过大变化。

选取东海试验中不同舰船辐射噪声信号D1～D5，分别应用扁平结构元素、三角结构元素和半圆结构元素计算20维GMPESE，结果如图5所示。

图5(a)在20维时间尺度上对舰船辐射噪声信号D1～D5有很好的区分度，图5(b)和图5(c)则在20维时间尺度上对舰船辐射噪声信号D1～D5区分度不佳。这一点同样证明了前文的论述，即相对半圆结构元素和三角结构元素，扁平结构元素因其对信号形状和幅值影响较小，信号失真度较低，因此应用扁平结构元素计算GMPESE特征区分度较好。

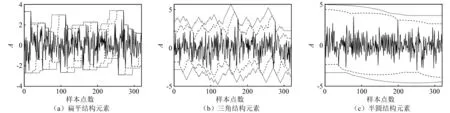
----为原信号； 为λ=10的膨胀与腐蚀运算； ……为λ=20的膨胀与腐蚀运算。图4 三种不同结构元素示意Fig.4 Three different kinds of structural elements

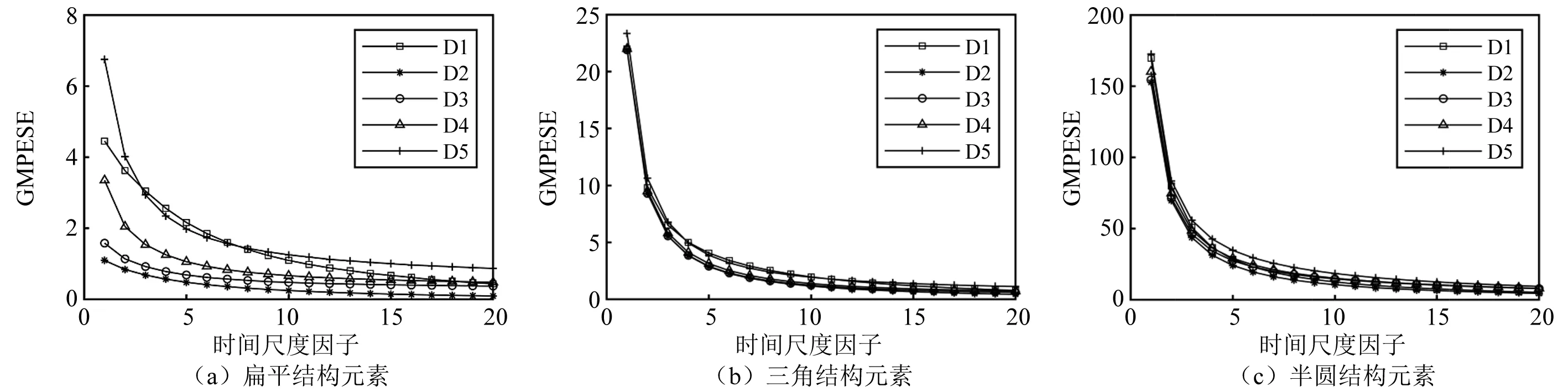
图5 应用不同结构元素的GMPESEFig.5 GMPESE of different kinds of structural elements

由式(14)可知，结构元素尺度因子λ和时间尺度因子τ取值均可影响GMPESE特征计算结果。而严格意义上来说，时间尺度因子并非结构元素的相关参数，但GMPESE特征的计算方法借鉴自MSE特征，在计算GMPESE特征的粗粒化过程中，时间尺度因子的值决定了粗粒化计算后时间序列的时长，进而影响该时间尺度下GMPESE特征计算结果，这与结构元素尺度因子对PES的影响机制相近。另一方面，时间尺度因子与结构元素尺度因子表现形式类似，因此将两者放在同一部分进行讨论。图6中：图6(a)为在计算GMPESE特征过程中，结构元素尺度因子λ取值对多尺度形态谱熵值的影响；图6(b)为在由PES计算GMPESE特征过程中，时间尺度因子τ的取值对GMPESE最终值的影响。明显可见当因子取值λ>20，τ>20时，PES和GMPESE变化幅度减小，甚至趋近平稳。在这种PES和GMPESE变化趋近平稳的情况下，该尺度因子取值对应的特征参数值对区分不同舰船目标贡献度很小，同时会增加计算复杂度，因此在计算GMPESE时取λ=20，τ=20。该结论与文献[17-18]一致。

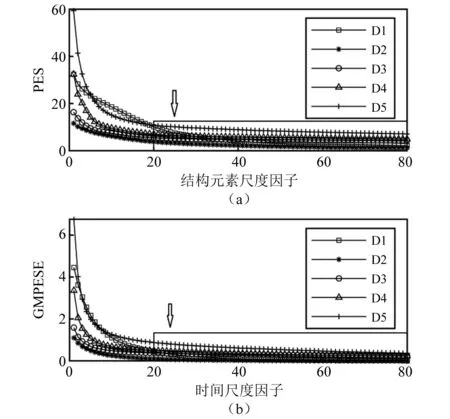
图6 两种尺度因子对特征参数计算影响Fig.6 The influence of structural element scale factors and time scale factors on the calculation of characteristic parameters

选定结构元素并确定结构元素尺度因子及时间尺度因子后，下一步应进行结构元素长度或高度参数选取。结构元素的参数选取并无明确准则，已有研究多依据经验参数进行取值。由于本文选用扁平结构元素进行数学形态学运算，本文以扁平结构元素参数的寻优为例，通过非经验方法进行选取结构元素参数的尝试，并给出一种基于猫群算法(cat swarm optimization，CSO)的寻优方法。CSO是一种由粒子群算法(particle swarm optimization，PSO)发展而来的寻优算法，本文借助CSO能跳出局部最优达到全局最优的特点对扁平结构元素的长度参数进行寻优。

此处参数寻优目的是寻找令目标识别准确率更高的结构元素长度参数，因此选取目标识别准确率作为适应度函数。参数优化的基本流程如图7所示。

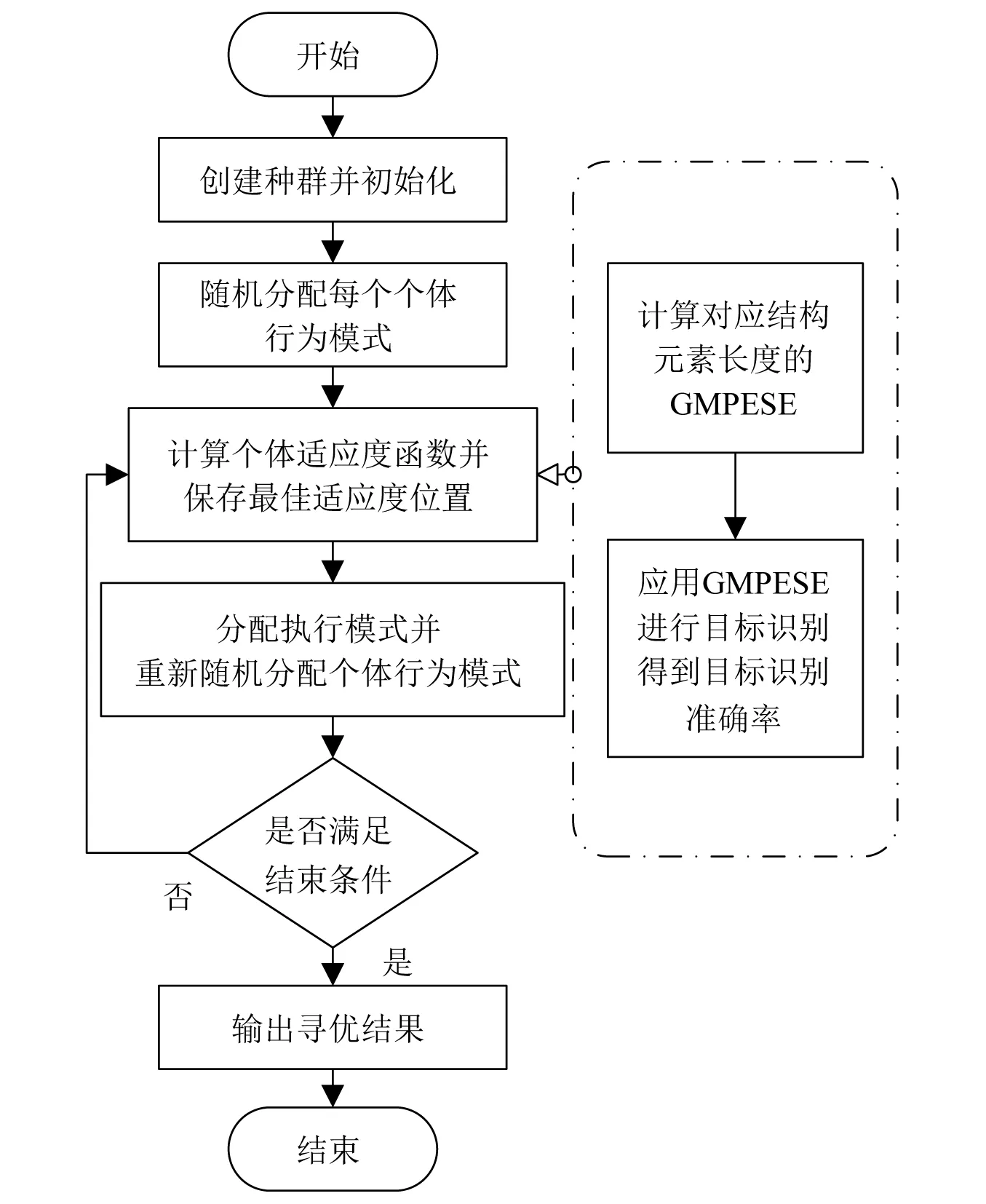
图7 结构元素参数优化流程Fig.7 Structural element parameter optimization process

与PSO相似，CSO种群规模与迭代次数越大，越容易跳出局部最优值，寻优效果越好，但同时也需要更多时间。为平衡寻优效果和耗费时长，设置种群规模为20，以迭代50次为结束条件，在1～50内寻找合适的结构元素长度。经过迭代运算后，得出最优长度为2，即g=[0,0]为最优扁平结构元素。

当结构元素g的长度取1～15时，提取的GMPESE特征用于舰船目标识别的准确率，如图8所示。由图8可知，当结构元素长度为2时目标识别准确率达到最大值，与寻优结果一致。

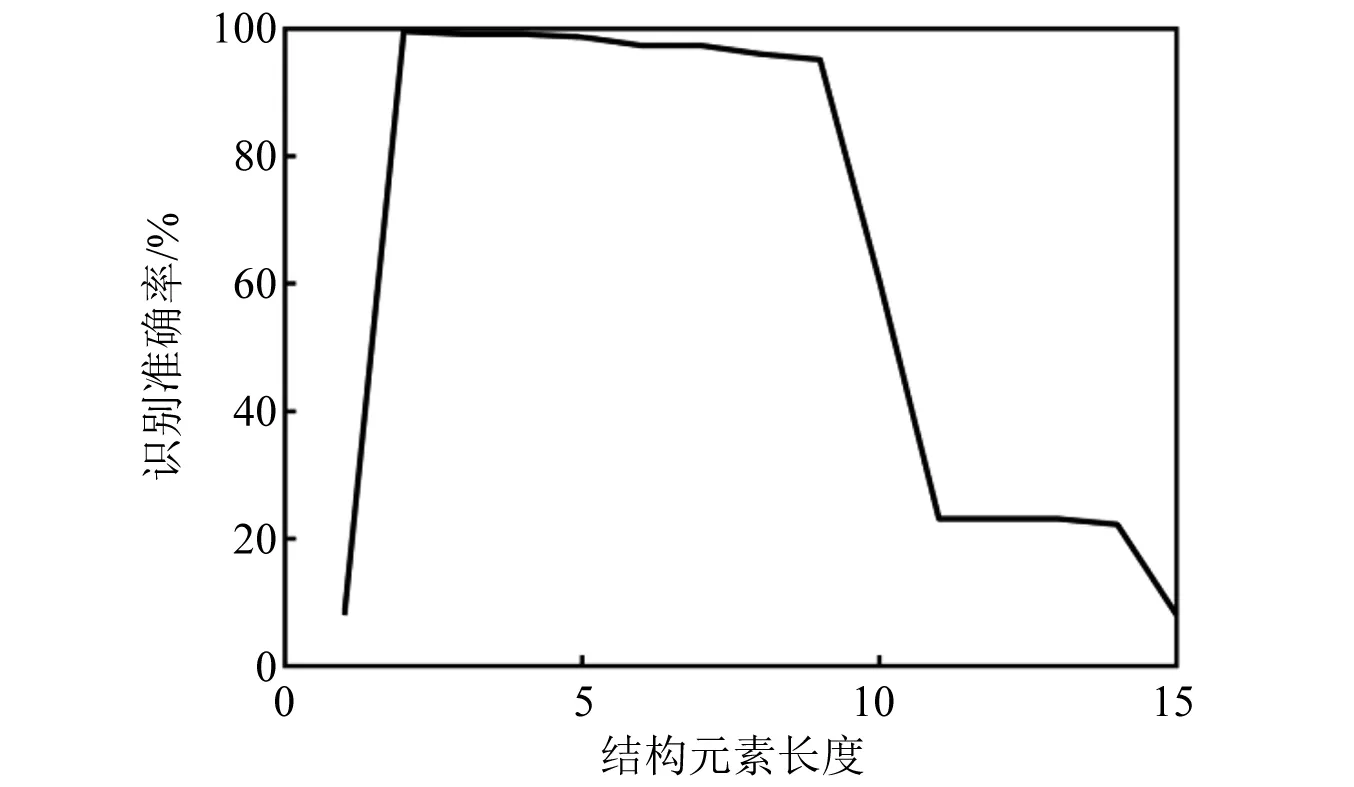
图8 目标识别准确率随结构元素长度的变化Fig.8 The trend of target recognition accuracy with the length of structural elements

本章以东海试验数据为例讨论了结构元素及其他参数选取对GMPESE特征的影响，得出如下结论：

(1) 扁平结构元素对原信号幅值及形状影响较小，更适用于舰船辐射噪声数学形态学运算。

(2) 结构元素尺度因子及时间尺度因子分别取λ=20，τ=20，结构元素取g=[0,0]更适合舰船辐射噪声GMPESE特征计算。

5 基于广义多尺度数学形态腐蚀谱熵的舰船目标识别

5.1 特征及区分度分析

GMPESE特征借鉴了MSE特征计算方法，与MSE的基本思想有相通之处，因此首先对不同目标舰船辐射噪声的GMPESE及MSE特征区分度进行比对分析。分别取410段及900段时长为1 s的千岛湖试验及东海试验中不同目标舰船辐射噪声，结构元素尺度因子及时间尺度因子分别取λ=20，τ=20，结构元素取g=[0,0]，计算其MSE及GMPESE，用SVM-RFE方法选取其前三阶特征参数，并进行对比，不同舰船辐射噪声在特征空间中的分布，如图9和图10所示。

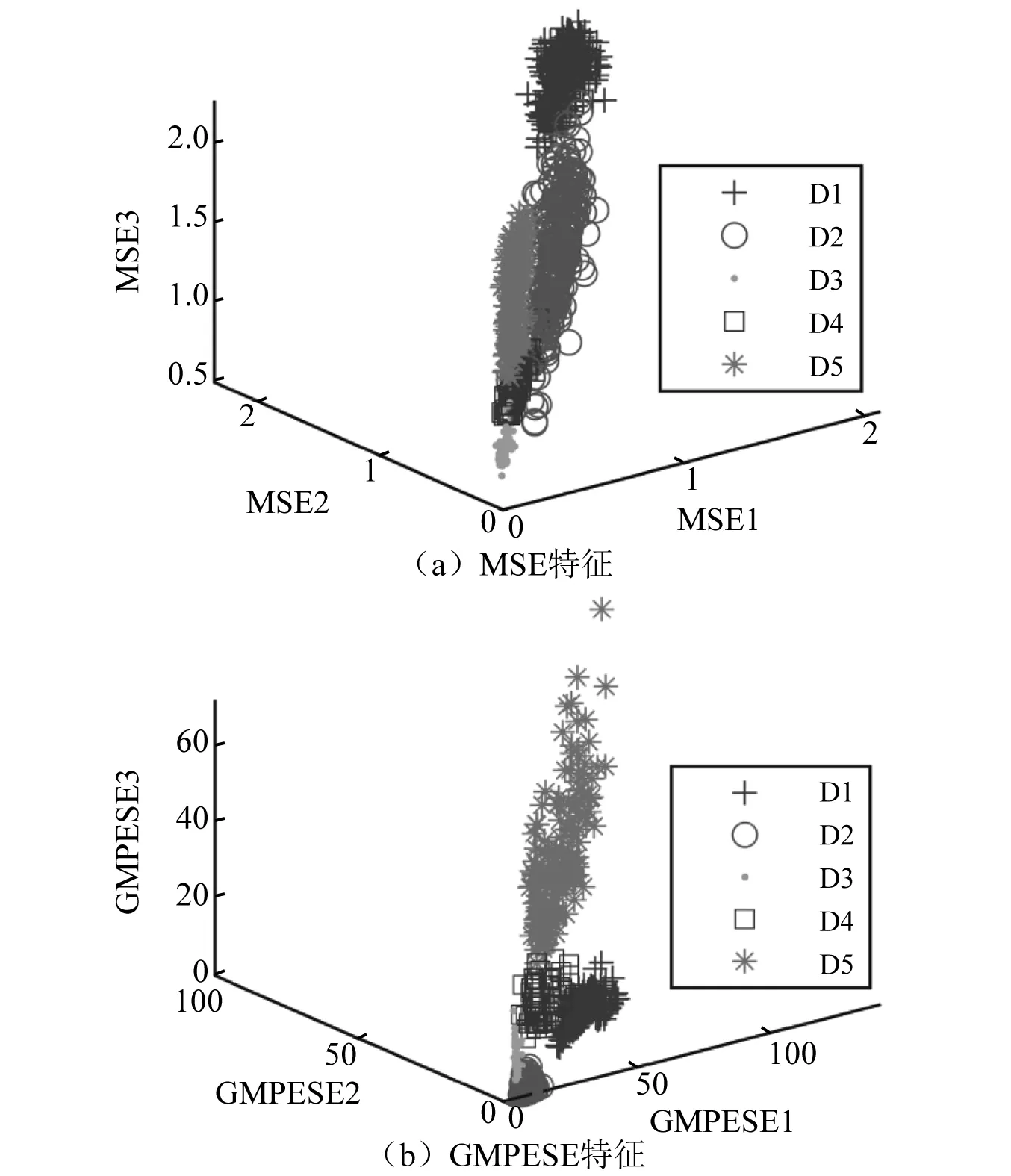
图9 不同舰船辐射噪声在前3维GMPESE与MSE特征空间中分布(东海)Fig.9 Different ship radiated noise’s distribution in the first three-dimensional GMPESE and MSE feature space (East China Sea)

图9(a)、图9(b)分别为东海试验中不同舰船辐射噪声的前3维MSE特征及GMPESE特征分布。由图9可知，在仅取前3维情况下，海试试验中5种目标舰船的GMPESE与MSE特征均有不错的区分度。图10(a)、图10(b)分别为千岛湖试验中不同舰船辐射噪声的前3维MSE特征及GMPESE特征分布。由图10可知：湖试试验中4种目标舰船的MSE特征在特征空间中有所重叠，但大致有一定区分度；4种目标舰船的GMPESE特征在特征空间有所重叠，但区分度好于MSE特征。考虑到东海试验和千岛湖试验中不同目标舰船之间差异程度并不相同，故而同样的特征提取方法应用于不同舰船辐射噪声数据得出的特征区分度不同。此外，经验证在去除前3维特征，仅使用排序靠后的若干维特征的情况下，仍可在一定程度上区分目标舰船。综上所述，可以作出推断：仅靠前3维特征可能并不能很好地识别不同舰船目标，提取多维特征有其必要性。

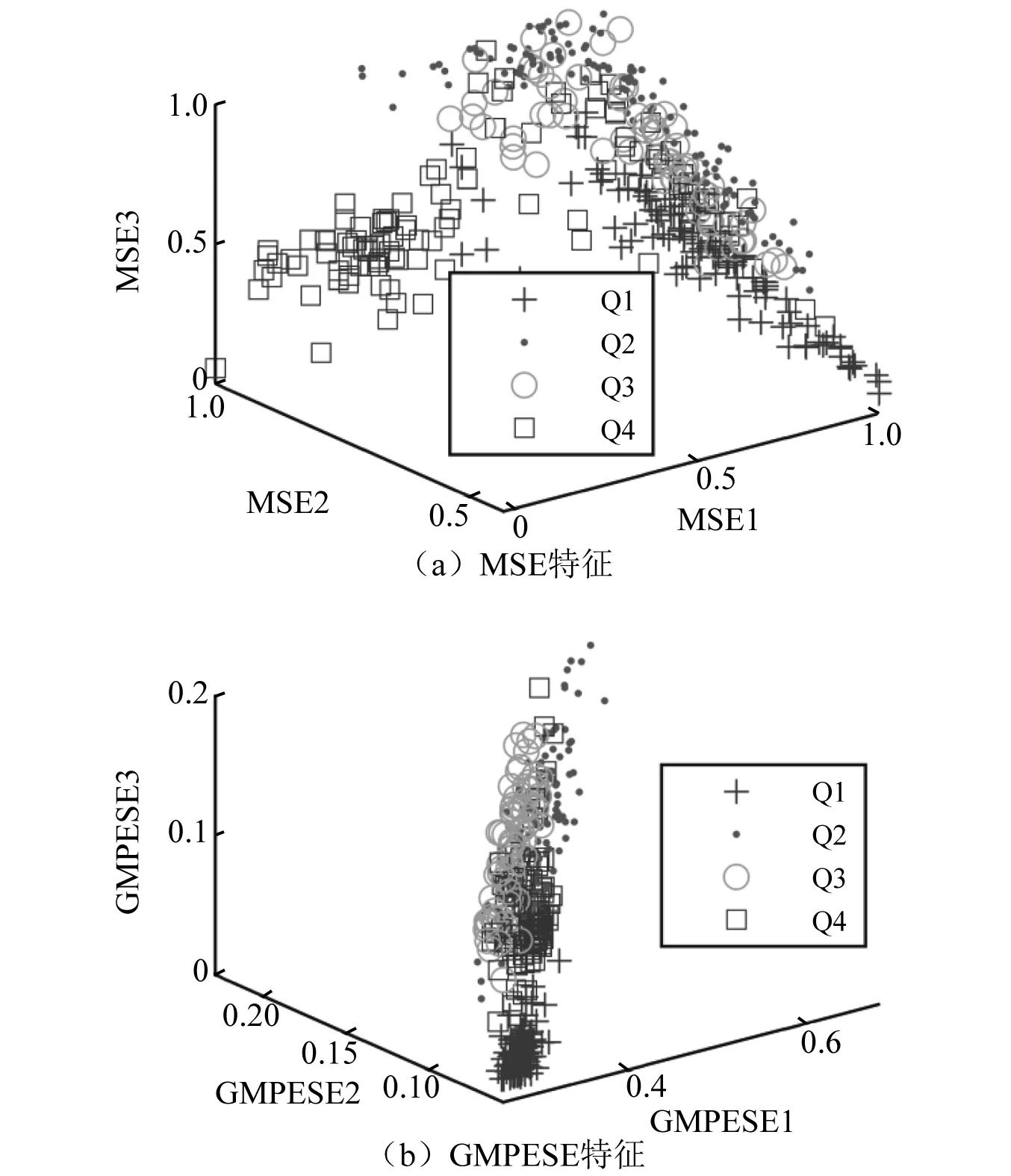
图10 不同舰船辐射噪声在前3维GMPESE与MSE特征空间中分布(千岛湖)Fig.10 Different ship radiated noise’s distribution in the first three-dimensional GMPESE and MSE feature space (Qiandao Lake)

5.2 舰船目标识别

在实际获取舰船辐射噪声信号时，很多时候难以保证水听器记录的信号都是有效的舰船辐射噪声信号，这也就意味着有效信号常是片段化的，从短时长的信号中提取的特征参数是否有效也是判断特征参数性能是否优秀的验证指标之一。因此，验证多尺度形态学方法对信号时长的依赖程度有其必要性。

分别取410段及900段时长0.1 s～1.0 s的千岛湖试验及东海试验中不同目标舰船辐射噪声，结构元素尺度因子及时间尺度因子分别取λ=20，τ=20，结构元素取g=[0,0]，计算MSE及GMPESE特征参数，记录其特征参数计算的运算耗时，并应用支持向量机进行识别，对比其识别准确率及运算耗时随信号时长的变化，如图11所示。

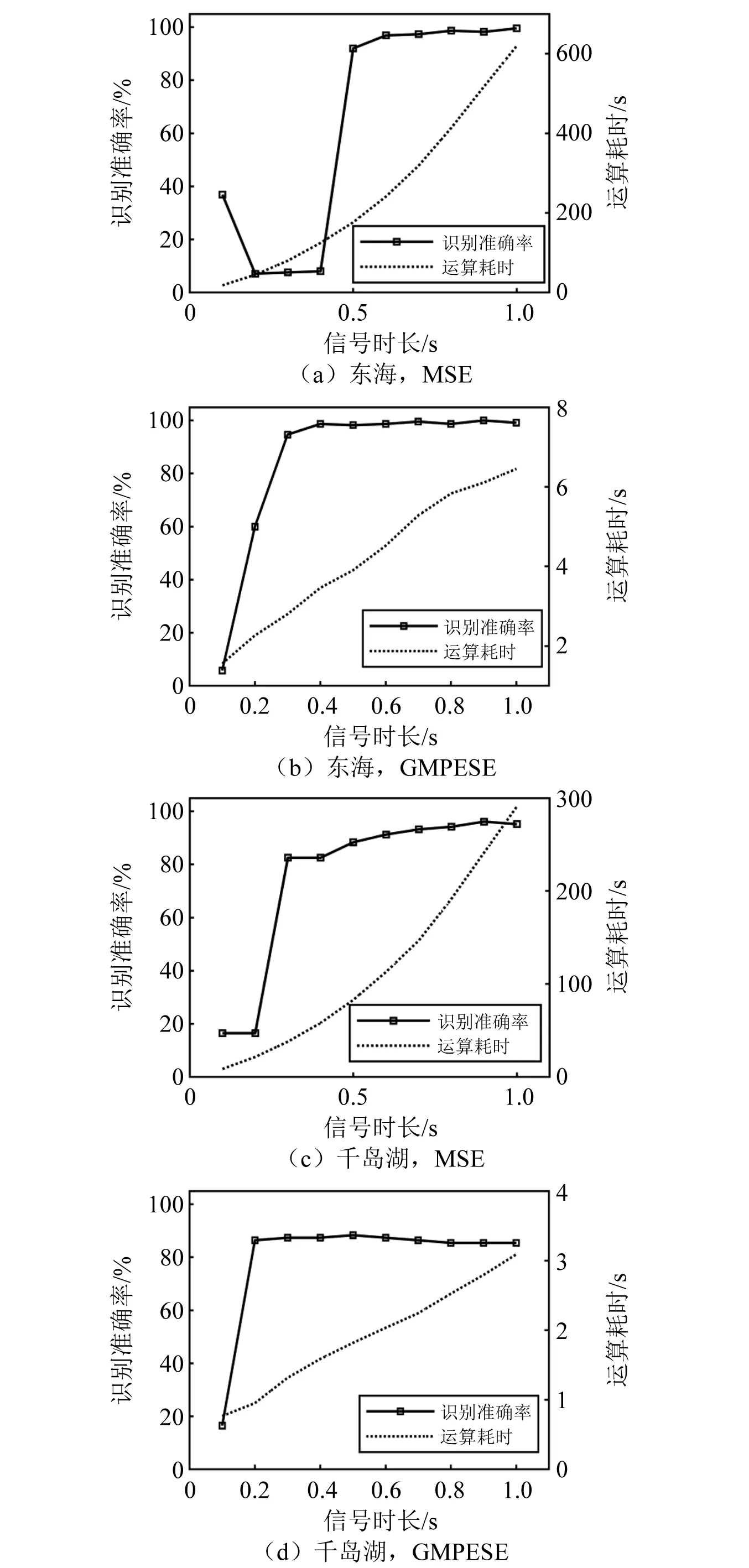
图11 MSE、GMPESE方法的目标识别准确率及运算耗时随信号时长的变化Fig.11 The target recognition accuracy and calculation time of MSE and GMPESE’s tendency with the signal duration

由图11(a)可知，MSE特征提取算法运算耗时与信号时长呈指数关系，即随着信号时长的增加，计算信号MSE特征的运算耗时及其增幅均明显增加，且在信号时长达到0.5 s时MSE特征才能稳定反映舰船辐射噪声的非线性特性，使舰船目标识别率达到92%的可接受水平；由图11(b)可知，GMPESE特征提取算法运算耗时可以近似看作信号时长的线性函数，在信号时长达到0.3 s时GMPESE特征即可稳定反映舰船辐射噪声的非线性特性，使舰船目标识别率达到94.67%的可接受水平；由图11(c)可知，MSE特征提取算法运算耗时与信号时长呈指数关系，计算信号MSE特征的运算耗时及其增幅均明显增加，且在信号时长达到0.3 s时MSE特征才能稳定反映舰船辐射噪声的非线性特性，使舰船目标识别率达到82.52%的可接受水平；由图11(d)可知，GMPESE特征提取算法运算耗时可以近似看作信号时长的线性函数，在信号时长达到0.2 s时GMPESE特征即可稳定反映舰船辐射噪声的非线性特性，使舰船目标识别率达到86.41%的可接受水平。综合对比图11(a)～图11(d)可知，GMPESE方法运算耗时明显远低于MSE，两者相差两个数量级；得到可用于舰船目标识别的稳定GMPESE特征所需的舰船辐射噪声信号时长，较MSE特征也更短。

图11(c)、图11(d)与图10结果相对照，同样证明了仅靠前3维特征并不能很好地区分不同舰船目标这一推断的合理性，因此实际应用中取τ=20，计算多维GMPESE是有必要的。

6 结 论

本文在数学形态学方法的基础上，提出一种广义多尺度数学形态腐蚀谱熵特征提取方法，并在此基础上对实测舰船辐射噪声进行了特征提取及目标识别，结果表明：

(1) 数学形态学方法能较好反映舰船辐射噪声的非线性特征，描述舰船辐射噪声复杂度的广义多尺度数学形态腐蚀谱熵特征可以作为不同目标舰船辐射噪声的有效识别手段。

(2) GMPESE特征仅涉及加减和取极值运算，因此计算效率高，运算耗时更少，适合实际工程应用。

(3) GMPESE特征计算所需信号时长更短(千岛湖环境0.2 s，东海环境0.3 s)，稳定性更好，适合实际水声环境下舰船目标识别。