输电塔线体系在摇摆地震动作用下的动力稳定性分析

魏文晖， 黄功伟， 徐辅中， 胡 郢

(武汉理工大学 道路桥梁与结构工程湖北省重点实验室，武汉 430070)

输电塔线体系作为典型的高柔钢结构体系，其动力稳定性问题是值得关注的[1]。以往针对输电塔线体系动力稳定性能的研究中，一般重点关注风荷载作用下结构的动力响应[2-4]。有关地震动摇摆分量研究现状指出摇摆分量对高度较大的结构不仅会增大结构动力响应的幅值，在往复的振动过程中造成地表产生残余倾斜，使结构产生单向偏移的非对称位移效应，这将对结构动力稳定性造成影响，甚至引起动力失稳[5]。

张行等[6]以干字型大跨输电塔为研究对象，将时程分析法与特征屈曲分析法相结合，探讨了此类结构在地震作用下的弹性动力稳定性能。李宏男等[7]为探究风荷载作用下输电塔结构的动态侧倾失稳，通过非线性屈曲和时程分析对输电塔的抗风动力稳定性进行了研究。吉柏锋等[8]基于输电塔主材失稳时弯矩-轴力-刚度关系，模拟了输电塔在下击暴流强风作用下输电塔受压失稳破坏全过程，并得到输电塔发生失稳时的薄弱杆件区域。伴随电网输送电压等级提高和特高压技术的广泛应用，塔线体系逐渐呈现出塔身高和非线性强的特点，地震对高柔输电塔线体系的破坏同样不可忽视。实际上，地震动是复杂的空间运动，除三向平动分量外，还包含摇摆分量[9-10]。部分学者研究了摇摆分量对结构地震响应的影响，如：Kalkan等分析了单自由度体系在考虑摇摆分量作用下的地震响应，研究结果表明摇摆分量会造成结构屈服后产生较大的非对称侧移；李宏男等[12-13]分析了大跨越输电塔线体系在水平与摇摆地震耦合作用下的反应，结果表明地震动摇摆分量对输电塔这类高柔结构影响很大，不应忽略。

本文基于现有研究，根据改进的谱比法获取地震动摇摆分量，探究了考虑地震动摇摆分量作用下输电塔线体系的动力稳定性能；然后进一步讨论地震动摇摆分量对高柔输电塔线体系动力稳定性能的影响。

1 摇摆分量获取

局限于当前地震动观测技术，无法直接测量并记录摇摆分量，研究所采用的地震动摇摆分量是由理论方法从地震动水平实测记录中获取。谱比法基于单摆式强震仪水平和竖向摆响应差异性，通过傅里叶变换得到地震动水平和竖向加速度傅里叶谱，对比差异确定特征频率，采用低通滤波的方式从水平分量中获取地震动摇摆分量时程。

选取的1994年美国Northridge地震中，可观测到地面的残余倾斜变形尤为明显，根据当时位于Pacoima水库左上桥墩站点记录显示地面倾斜位移约3.1°，本研究在谱比法的基础上，采用小波变换和小波阈值去噪替代傅里叶变换和低通滤波，对谱比法进行优化，而后根据改进的谱比法，对Northridge地震波进行处理进而提取相应的地震动摇摆分量时程。Northridge地震中震区站点实测加速度数据，如图1和图2所示；获取的Northridge地震动摇摆转角位移时程和摇摆加速度时程结果，分别如图3和图4所示。

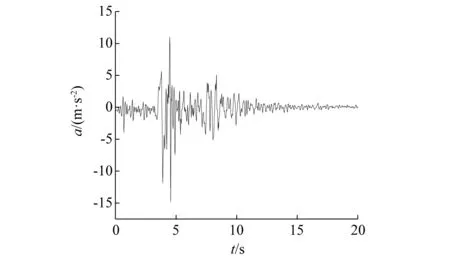
图1 Northridge地震动水平加速度时程Fig.1 Horizontal time history from Northridge earthquake

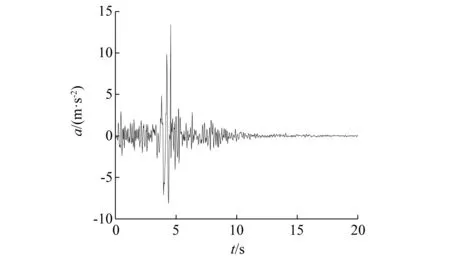
图2 Northridge地震动竖向加速度时程Fig.2 Verticaltime history from Northridge earthquake

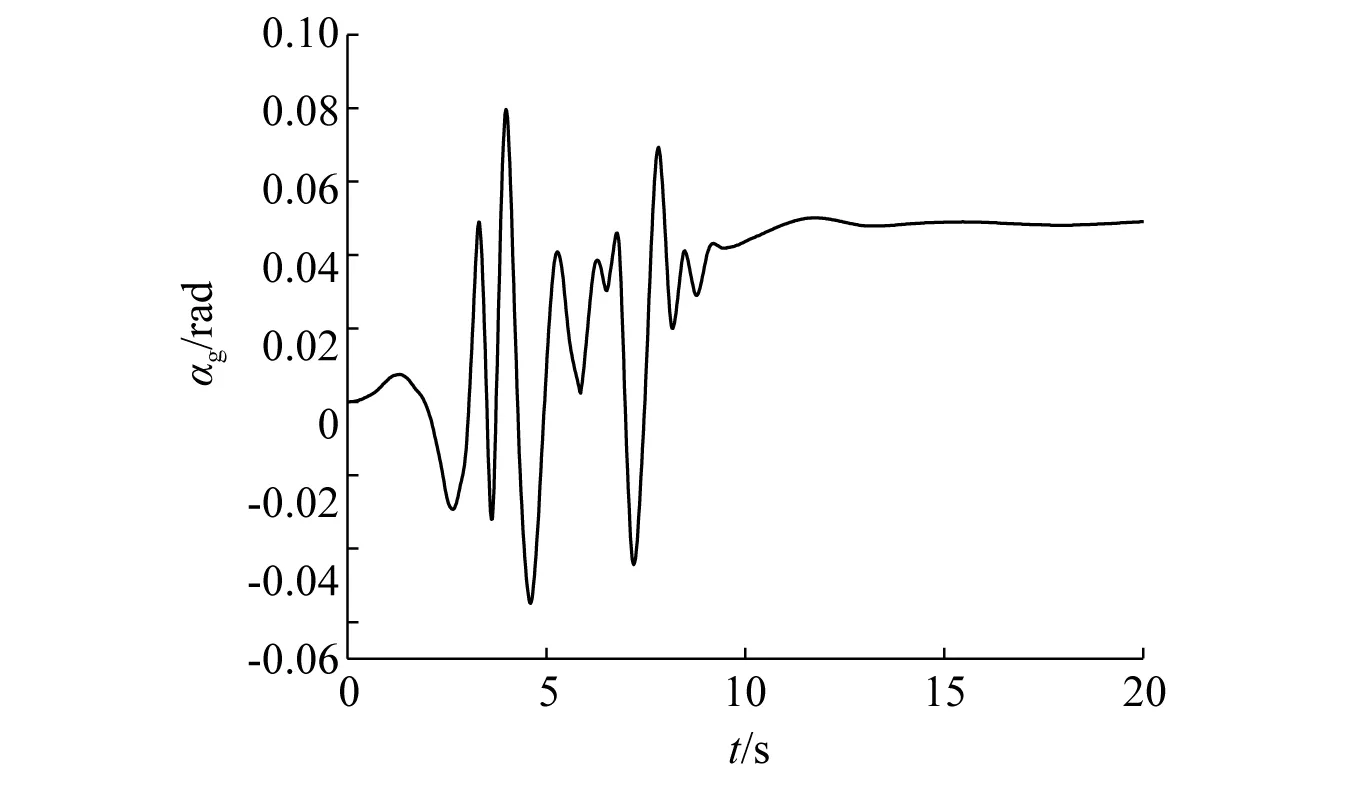
图3 Northridge地震动摇摆转角位移时程Fig.3 Time history of tilt displacement of Northridge earthquake

图4 Northridge地震动摇摆加速度时程Fig.4 Time history of tilt acceleration of Northridge earthquake

2 动力稳定性计算方法

输电塔线体系在地震作用下的动力稳定属于任意动力荷载作用下的结构动力稳定性问题。此类问题因实际工程结构的复杂性和地震波的特点难以采用经典理论方法去解决，目前有效的求解方法是采用数值计算获得结构运动全过程时程曲线来判别其稳定性。

2.1 B-R准则

B-R准则最早由Budiansky与Roth两位学者提出，该准则选取直观的物理量作为判据，通过动力微分方程求出的响应和荷载之间的关系曲线，把微小的荷载增量引起结构特征响应突然急速增大时刻判定为结构发生动力失稳，并将此时的荷载定义为结构的失稳临界荷载。本质与Lyapunov意义上的运动失稳一致[14]。

2.2 增量动力分析方法

增量动力分析(incremental dynamic analysis，IDA)方法是一种全过程的结构动力分析方法。该方法对同一地震波，按比例逐级放大地震动峰值加速度后对结构依次进行非线性时程分析，得到结构在不同强度地震作用下的响应情况。根据结构特点选取强度度量 (intensity measure, IM)和损伤度量(damage measure, DM)；然后分别以IM和DM为横、纵坐标，描点连线即可得到结构在地震作用下IDA曲线。该曲线能够反映出结构动力响应、侧向刚度和变形能力等指标随地震强度的变化过程[15]。

IDA方法结合B-R准则能较好的解决复杂工程结构动力稳定性问题。通过对大跨桥梁、高墩桥梁的墩柱以及网壳等结构的研究表明，结构发生动力失稳时部分截面或局部杆件截面会进入塑性状态并发生动力失稳造成结构局部刚度减小或出现刚度矩阵非正定的情况，体现在IDA曲线上则会出现明显的拐点，并可由此来确定结构发生动力失稳的时刻和动力失稳临界荷载。IDA分析方法结合B-R准则判断输电塔线体系动力稳定性的具体步骤如下：

步骤1将特定地震波根据其加速度幅值PGA按单调递增的比例逐步增大；

步骤2采用步骤1中得到的不同强度的地震波，对输电塔线体系进行非线性动力时程分析，选取塔顶最大位移作为特征响应指标，记录每一次时程分析结构的最大特征响应；

步骤3将步骤2中记录的每一次时程分析中最大特征响应和地震动峰值加速度作为横纵坐标，描点连线即可得到塔线体系的IDA曲线；

步骤4采用B-R准则，当IDA曲线出现明显拐点，即可确定结构发生动力失稳，并可得动力失稳时刻和动力失稳临界荷载。

3 输电塔体系动力稳定性分析

3.1 有限元模型建立

以实际工程输电线路中某高压直线型输电塔线体系为依据，建立输电塔线体系有限元模型。塔身整体高度为81.8 m，横担长度为35.4 m，塔体底部间距为17.18 m×17.18 m，塔身横截面尺寸由下自上逐渐减小为3.8 m×3.8 m，塔距500 m，导线直径29.14 mm，质量1 856.7 kg/km。塔身杆件均为等边角钢，主材采用Q420钢，斜材和辅材分别为Q345钢和Q235钢。导线为单回路直流两相导线，每相导线四分裂，忽略地线影响。采用ANSYS有限元软件进行建模，输电塔身杆件选择BEAM188单元进行模拟，采用双线性随动强化模型(bilinear kinematic，BKIN)模拟输电塔角钢材料非线性性能；结合输电导线的受力特性，采用LINK10单元来进行模拟导线，选取瑞雷阻尼来考虑输电塔在振动过程中的耗能特性，最终建立的输电塔线体系如图5所示。其中输电塔线体系为“三塔两线”模型，包含三座输电塔和两跨导线，中间塔体为待研究的输电塔，即采用考虑材料非线性和几何非线性的输电塔；两边塔体作为边界塔，起到架设导线，最大程度模拟实际边界的作用，建模时对其进行必要的简化。摇摆分量绕横线向输入，选取输电塔线体系顺线向作为水平地震不利输入方向，地震波竖向分量沿输电塔线体系模型竖直方向输入。

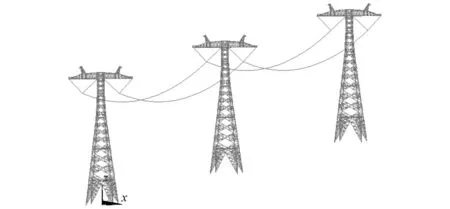
图5 “三塔两线”有限元模型Fig.5 Finite element model of “three towers and two lines”

对于输电塔线体系，由于导线的存在，大多数模态分析结果均是以导线振动为主的模态，选取了塔线体系的前三阶模态和前1 000阶模态中以中间待研究塔体振动为主的前四阶典型模态，如表1所示。

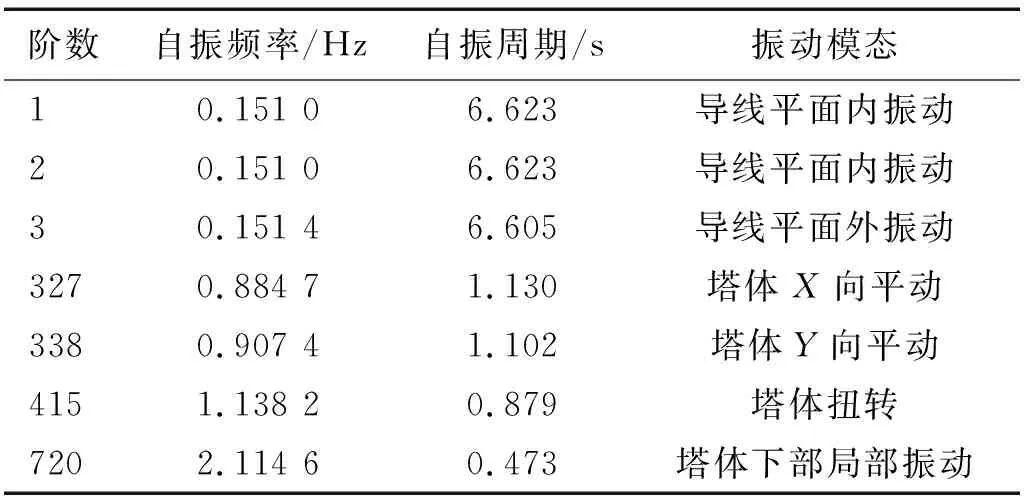
表1 输电塔线体系自振频率和自振周期Tab.1 Natural vibration frequency and natural vibration period of transmission tower-line system

将输电单塔和输电塔线体系以塔身振动为主的前三阶模态进行对比，结果如表2所示。无论是沿X，Y方向的平动还是塔身绕Z轴的扭转，输电塔线体系的自振频率均小于单塔模型，可见导线对输电塔的动力性能是有影响的，因此对输电塔进行动力稳定性分析时，考虑输电单塔与导线的整体建模是有必要的。

表2 输电单塔和塔线体系自振频率对比Tab.2 Comparison of natural frequencies between single tower and tower-line system

3.2 三种工况动力稳定性分析

基于“三塔两线”输电塔线体系有限元模型，选取IDA分析和B-R准则相结合的计算方法判断塔线体系动力稳定性，研究输电塔线体系在水平地震作用、水平-摇摆耦合地震作用以及水平-竖向-摇摆耦合地震作用三种工况下的动力稳定性能，并进行对比分析，讨论地震动摇摆分量对输电塔线体系动力稳定性能的影响，时程分析所用的地震波选取前述Northridge地震波，其水平加速度时程、竖向加速度时程和摇摆加速度时程曲线分别见图1、图2和图4。

3.2.1 水平工况

单一水平地震作用下，根据所选取强度度量(peak ground acceleration，PGA)和特征响应(塔顶最大位移)绘制IDA曲线，得到水平地震作用下输电塔线体系IDA曲线，如图6所示。不同PGA输电塔顶部位移时程曲线，如图7所示。输电塔线体系在失稳临界加速度下变形图，如图8所示。

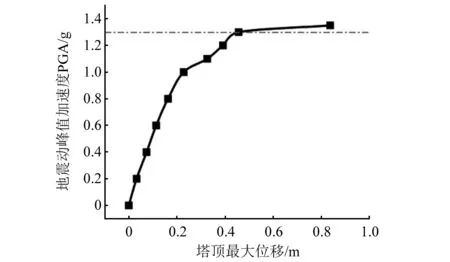
图6 水平工况塔线体系IDA曲线Fig.6 IDA curve of horizontal tower-line system

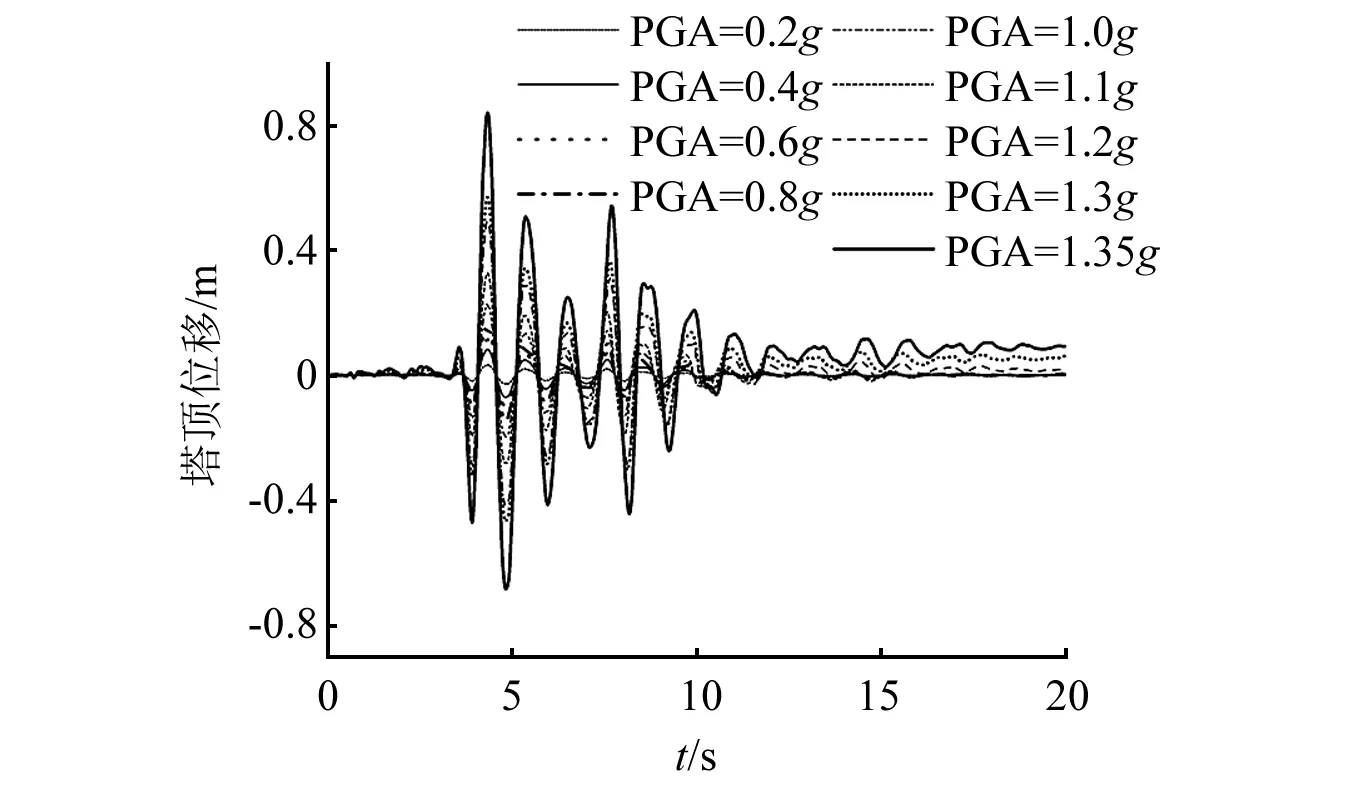
图7 水平工况塔顶位移时程曲线Fig.7 Time history curve of tower top displacement under horizontal condition

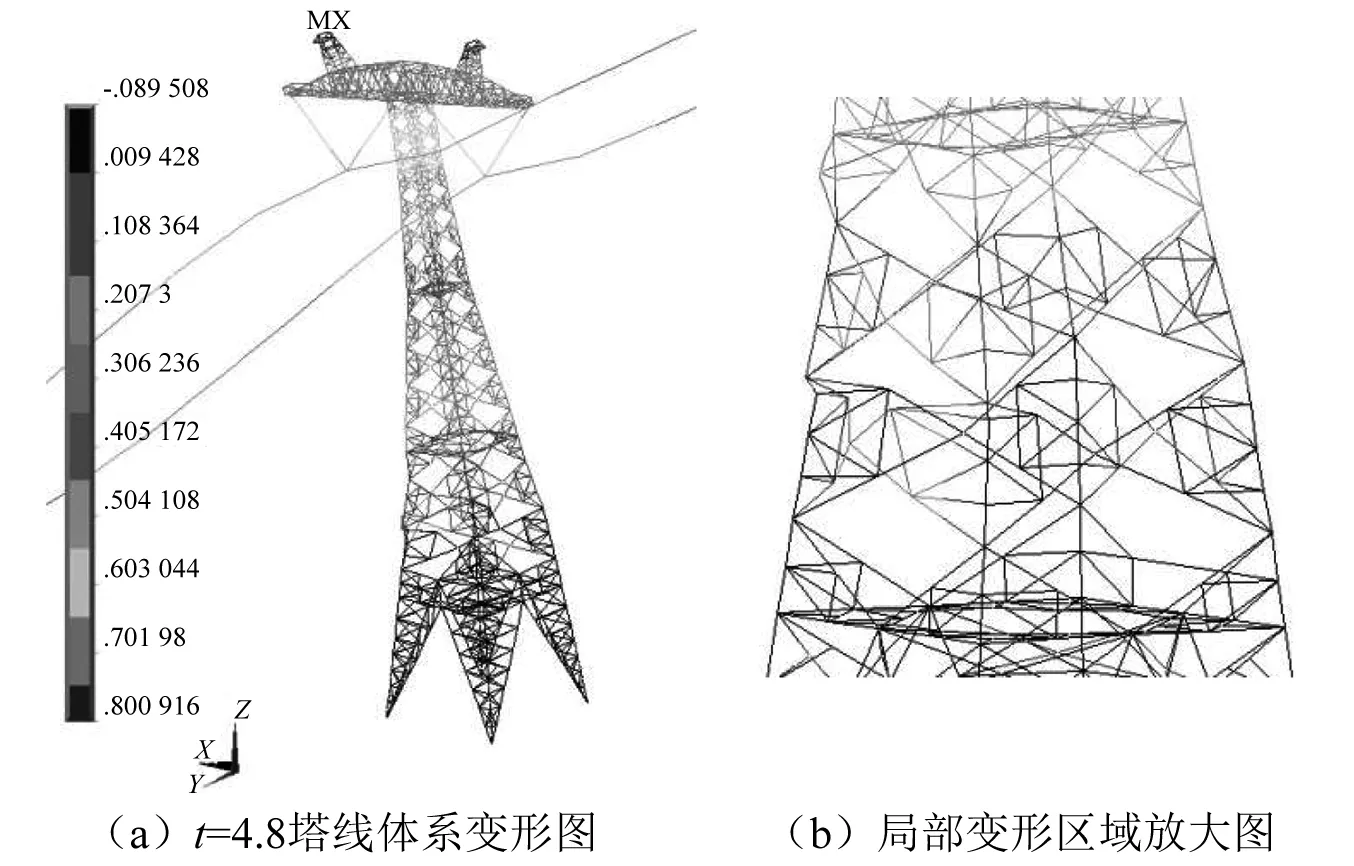
图8 水平工况塔线变形图Fig.8 Deformation diagram of tower-line system under horizontal condition

由图6和图7可以看出，PGA增大到1.1g，IDA曲线开始出现转折，塔体顶部位移最大值达到0.326 m。继续增大地震动峰值加速度，输电塔线体系进入非线性状态，塔顶水平位移曲线出现单向偏移，当地震动加速度幅值达到1.3g时，IDA曲线出现明显拐点。再增加微小增量，达到1.35g时，位移响应单向偏移趋势进一步增大，虽然位移并未出现发散式的增大，但IDA曲线出现明显拐点，说明塔体局部刚度出现了明显的变化。根据B-R准则可以判断，输电塔线体系出现动力失稳，失稳临界荷载为1.35g，但结构尚未彻底丧失承载能力。

3.2.2 水平-摇摆工况

水平-摇摆耦合地震作用下输电塔线体系IDA曲线，如图9所示。不同PGA输电塔顶部位移时程曲线，如图10所示。输电塔线体系在失稳临界加速度下变形图，如图11所示。

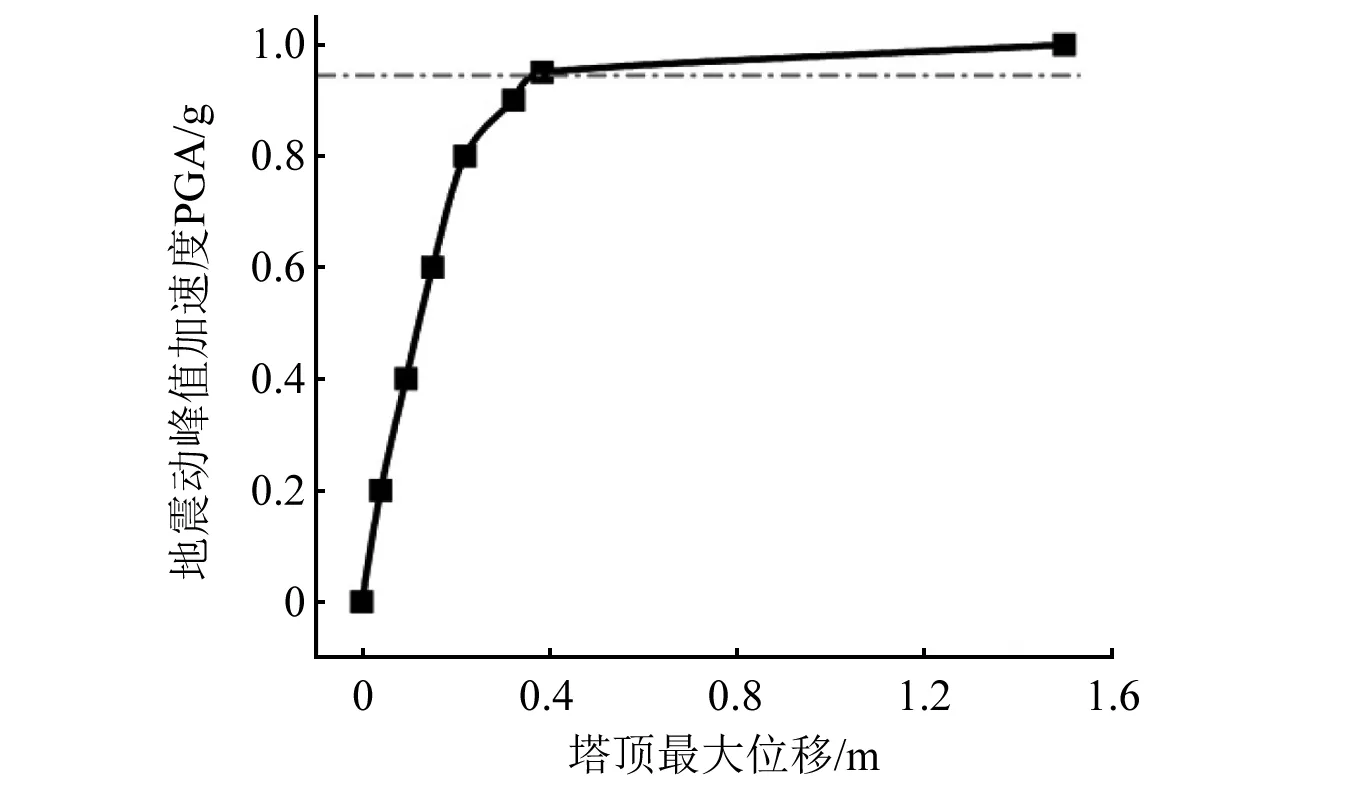
图9 水平-摇摆耦合工况塔线体系IDA曲线Fig.9 IDA curve of tower-line system under horizontal-tilting coupling condition

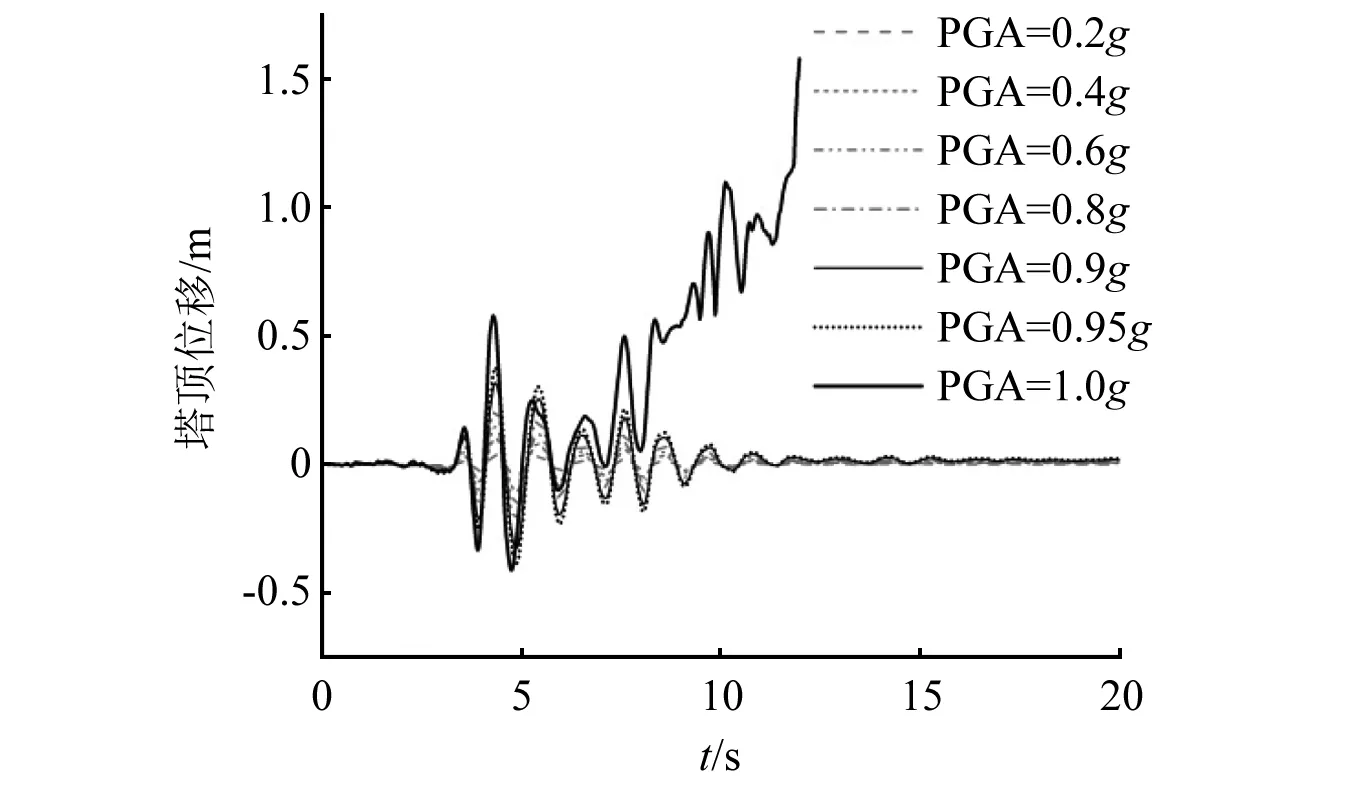
图10 水平-摇摆耦合工况塔顶位移时程曲线Fig.10 Time history curve of tower top displacement under horizontal-tilting coupling condition

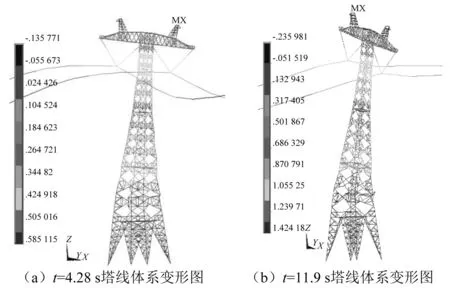
图11 水平-摇摆耦合工况塔线体系变形图Fig.11 Deformation diagram of tower-line system under horizontal-tilting coupling condition

由图9和图10可以看出，IDA曲线拐点对应的地震动加速度幅值小于水平地震作用下的幅值，输电塔线体系在地震动峰值加速度为0.95g时，IDA曲线开始出现转折，塔顶位移最大值达到0.324 m。当地震动幅值再增大0.05g，达到1.0g时，位移时程曲线出现明显单向增大的非对称趋势，表明结构偏离竖向平衡位置，产生非对称振动；11.9 s后结构位移急速增大直至发散，即微小的荷载增量引起结构特征响应剧烈变化，根据B-R准则可以判定，输电塔线体系发生动力失稳，失稳临界加速度为1.0g。结合输电塔线体系失稳临界加速度下的变形图可以看出，t=4.28 s时塔身中下部发生局部变形，塔顶最大位移为0.584 m；当t=11.9 s时输电塔线体系塔顶位移已经很大，达到1.42 m，此时塔线体系在水平-摇摆耦合地震作用下失去整体动力稳定性能，结合图3 Northridge地震动摇摆转角位移时程图，可以看出摇摆分量在地震作用的中后期向一侧单向运动，会引起基础倾斜，塔身出现倾倒趋势。

3.2.3 水平-竖向-摇摆工况

考虑竖向分量后，水平-竖向-摇摆地震作用下输电塔线体系IDA曲线，如图12所示。不同PGA下输电塔顶部位移时程曲线，如图13所示。输电塔线体系在失稳临界加速度下变形图，如图14所示。

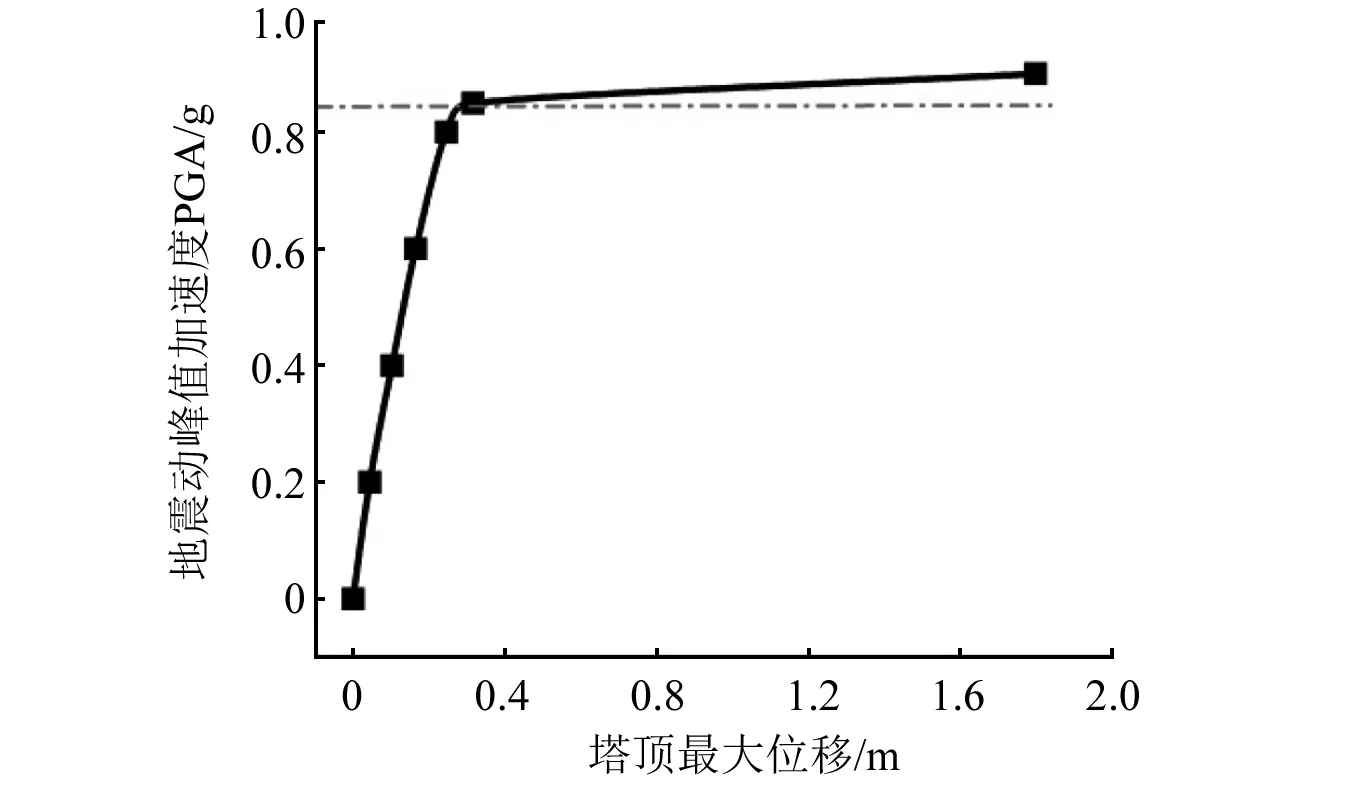
图12 水平-竖向-摇摆耦合工况塔线体系IDA曲线Fig.12 IDA curve of tower line-system under horizontal-vertical-tilting coupling condition

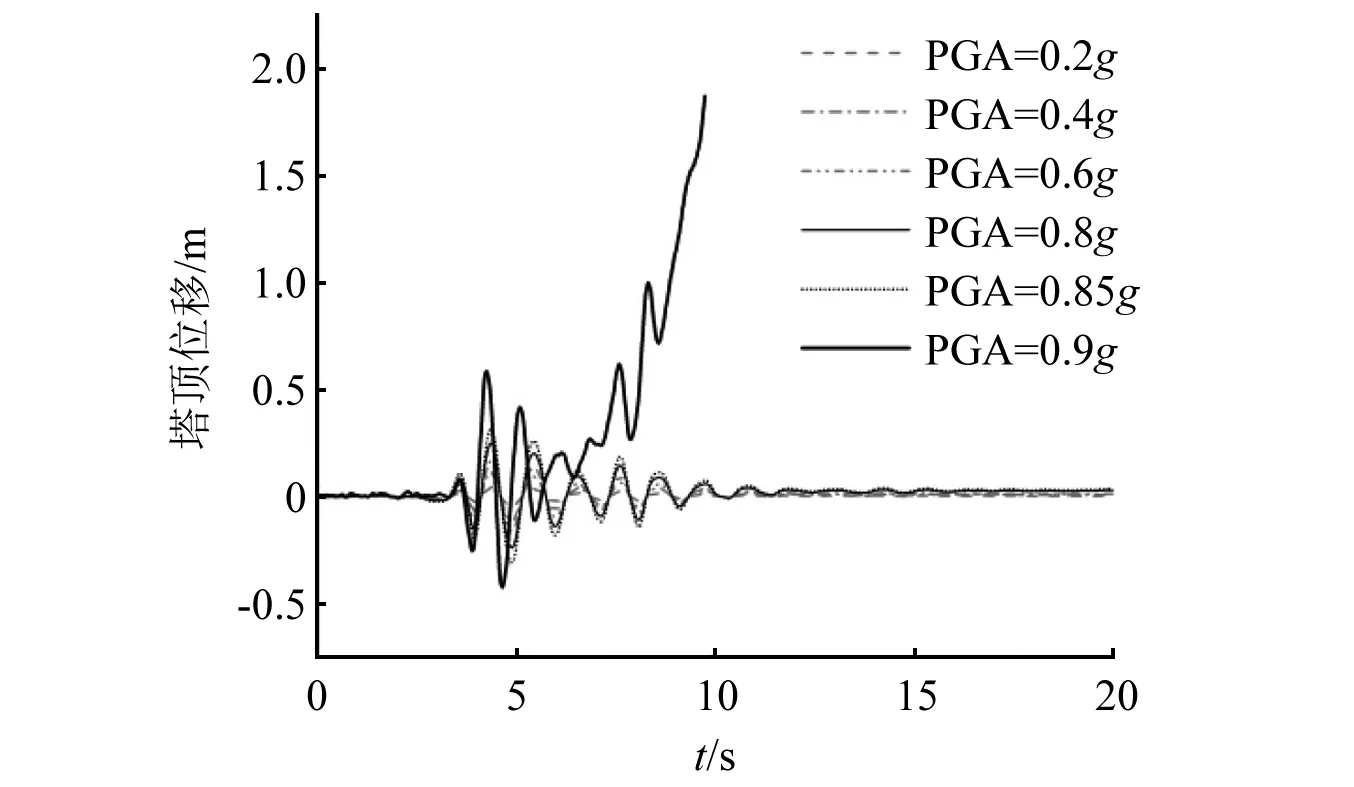
图13 水平-竖向-摇摆耦合工况塔顶位移时程曲线Fig.13 Time history curve of tower top displacement under horizontal-vertical-tilting coupling condition

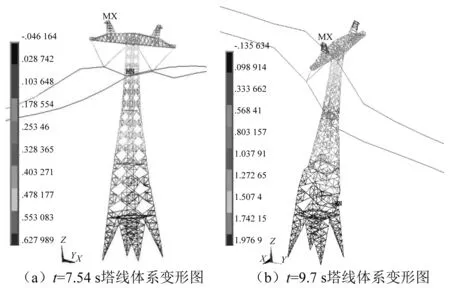
图14 水平-竖向-摇摆耦合工况塔线体系变形图Fig.14 Deformation diagram of tower line-system under horizontal-vertical-tilting coupling condition

由图12和图13可以看出，IDA曲线拐点对应的地震动加速度幅值相较水平-摇摆工况进一步有所减小。输电塔线体系在地震动峰值加速度为0.85g时，IDA曲线开始出现转折，塔顶位移最大值达到0.316 m。当地震动加速度幅值再增大0.05g，达到0.9g时，位移时程曲线出现明显单向增大的非对称趋势，9.7 s后输电塔线体系顶部特征位移急速增大，即微小的荷载增量引起结构特征响应剧烈变化，根据B-R准则可以判断，输电塔线体系出现动力失稳，失稳临界加速度为0.9g。结合输电塔线体系失稳临界加速度下结构变形图可以看出，t=7.54 s时塔身中下部变形开始增大，出现偏离平衡位置的非对称振动，塔顶位移达到0.628 m；t=9.7 s时输电塔线体系塔顶位移已经很大，达到1.97 m，此时塔线体系在水平-竖向-摇摆耦合地震作用下失去整体动力稳定性能，塔身出现倾倒趋势。

3.3 对比分析

为分析地震动摇摆分量对输电塔线体系动力稳定性能产生影响的原因，首先讨论摇摆分量对输电塔线体系动力响应的影响。选取三种分析工况，地震动峰值加速度分别为0.2g，0.4g，0.8g和动力失稳临界加速度下输电塔线体系塔顶位移时程曲线进行对比，如图15～图18所示。

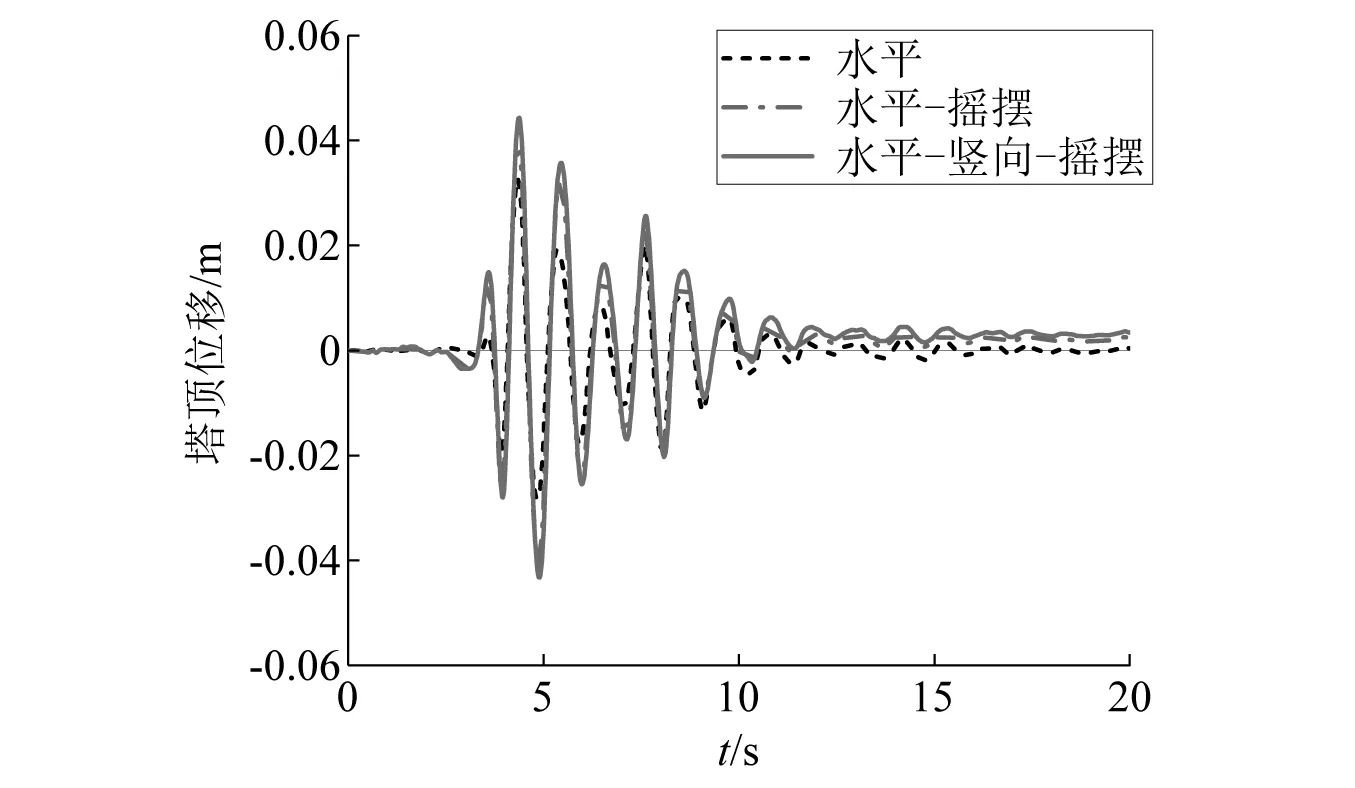
图15 PGA=0.2g塔顶位移时程Fig.15 PGA=0.2g time history of displacement on top tower

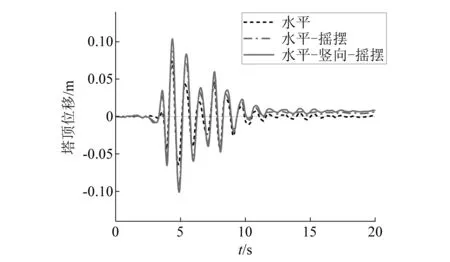
图16 PGA=0.4g塔顶位移时程Fig.16 PGA=0.4g time history of displacement on top tower

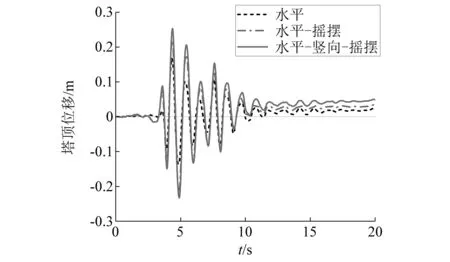
图17 PGA=0.8g塔顶位移时程Fig.17 PGA=0.8g time history of displacement on top tower

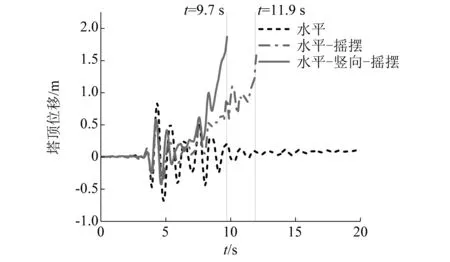
图18 动力失稳临界加速度下塔顶位移时程Fig.18 Time history of displacement on tower top under critical acceleration of dynamic buckling

地震动峰值加速度较小时，如PGA为0.2g和0.4g，单一水平地震作用下，输电塔线体系塔顶位移时程曲线始终沿0基线上下波动。而水平-摇摆和水平-竖向-摇摆工况下，输电塔线体系塔顶位移时程曲线均偏离0基线，即塔线体系发生非对称振动现象。随着地震动峰值加速度增大结构进入非线性振动阶段，PGA达到0.8g时，单一水平地震作用下塔顶位移时程曲线也出现了偏离0基线的现象。考虑摇摆分量后，水平-摇摆耦合地震作用下，相较于单一水平工况位移时程曲线偏移现象更加明显，考虑竖向分量影响后，塔顶位移偏移进一步增大。

随着地震动峰值加速度进一步增大，水平-摇摆工况，动力失稳临界加速度下塔顶位移时程曲线出现明显单向偏移，位移不断单向增大，表明在振动过程中塔身变形沿着单一方向不断积累，这主要是由于结构自身产生的非线性变形与摇摆位移转角及其引起的附加P-Δ效应共同作用所导致。当塔身非对称变形积累到一定程度，塔顶位移达到1.5 m左右时，位移曲线在11.9 s后急速增大直至发散，输电塔线体系发生动力失稳破坏。水平-竖向-摇摆工况，输电塔线体系在动力失稳临界加速度下的塔顶位移时程曲线同样出现明显的单向偏移，相较于水平-摇摆工况，输电塔线体系在水平-竖向-摇摆工况下，塔顶位移更早出现单向偏移现象，过大的单向侧移积累导致输电塔线体系塔顶位移在9.7 s后就出现急速单向增大直至发散的现象，表明竖向地震作用会导致输电塔线体系失稳破坏的速度加剧。这主要是由于临界状态下塔身产生不可恢复的非线性变形与摇摆位移转角及其引起的附加P-Δ效应共同作用下，使塔体发生较大偏移，而竖向地震作用将导致结构P-Δ效应增大，会进一步放大摇摆分量对结构动力稳定性能的影响。

可见在强震作用下，结构达到非线性阶段后，摇摆分量对结构动力响应所造成的影响远大于弹性阶段所产生的影响。强震作用下，摇摆转角位移及其造成的附加P-Δ效应，会进一步导致结构发生偏离平衡位置的单向偏移振动，使结构变形有沿着一个方向累积的趋势，当输电塔线体系单向变形的积累到一定程度时，势必对其动力稳定性能产生不利影响，甚至引发动力失稳破坏。

输电塔线体系在三种分析工况下IDA曲线对比图，如图19所示。三种分析工况下输电塔线体系失稳临界加速度和失效时刻，如表3所示。下面将对输电塔线体系在水平地震作用、水平-摇摆耦合地震作用和水平-竖向-摇摆耦合地震作用下的动力稳定性能进行对比分析。由图19和表3可以看出：输电塔线体系在单一水平地震作用下动力失稳临界加速度为1.35g，考虑摇摆分量影响后，输电塔线体系在水平-摇摆耦合地震作用下动力失稳临界加速度为1.0g，相较单一水平地震作用下，塔线体系动力失稳临界加速度峰值降幅达到25.9%，可见摇摆分量对输电塔线体系这类高柔结构的动力稳定性能有显著影响；此外，考虑竖向地震作用影响后，水平-竖向-摇摆耦合地震作用下输电塔线体系动力失稳临界加速度为0.9g，相较单一水平地震作用降幅达到33.3%，相较水平-摇摆耦合地震作用降幅为10%，表明耦合竖向地震作用后会进一步降低塔线体系在地震作用下的动力失稳临界加速度。

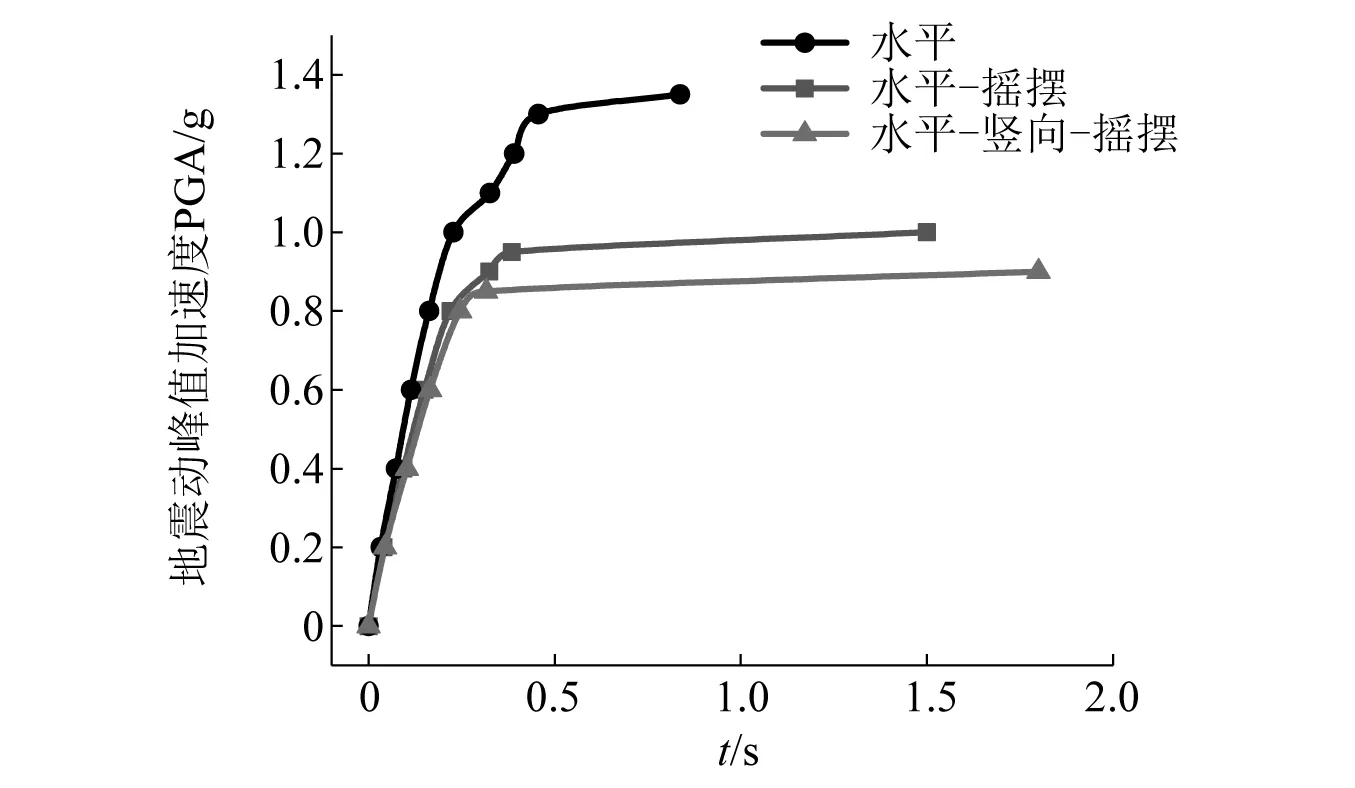
图19 三种工况下IDA曲线对比Fig.19 IDA curve comparison under three working conditions

表3 三种工况下动力失稳临界加速度和失效时刻Tab.3 Critical acceleration and failure time of dynamic buckling under three working conditions

上述讨论了地震动摇摆分量对输电塔线体系动力稳定性能的影响，下面将进一步探究塔线体系在地震作用下的失稳破坏机理，由于单向水平地震作用下输电塔线体系具有较好的动力稳定性能，并未出现倾倒失效的现象，因此仅对水平-摇摆耦合地震作用下输电塔线体系的失稳破坏机理进行分析。

从图20可以看出，输电塔线体系整体失效形态，具有塔身上部位移大，变形小；而中下部则表现为位移小，变形大的特征。引起塔身发生整体失效倒塌的杆件破坏的主要部位在输电塔中上部与中下部连接处，距离地面20～40 m内塔身区域。因此，输电塔线体系在考虑地震动摇摆分量作用下发生动力失稳破坏时塔身薄弱区域为第二节间，对输电塔线体系进行抗震设计时应该适当增大塔身中下部薄弱区域杆件截面面积，提高结构整体承载能力和抗变形能力，以预防强震引起构件失效引发结构整体动力失稳。水平-竖向-摇摆耦合地震作用下塔线体系失稳破坏形式与水平-摇摆耦合地震作用下的破坏形式类似，由于篇幅限制不再分析。

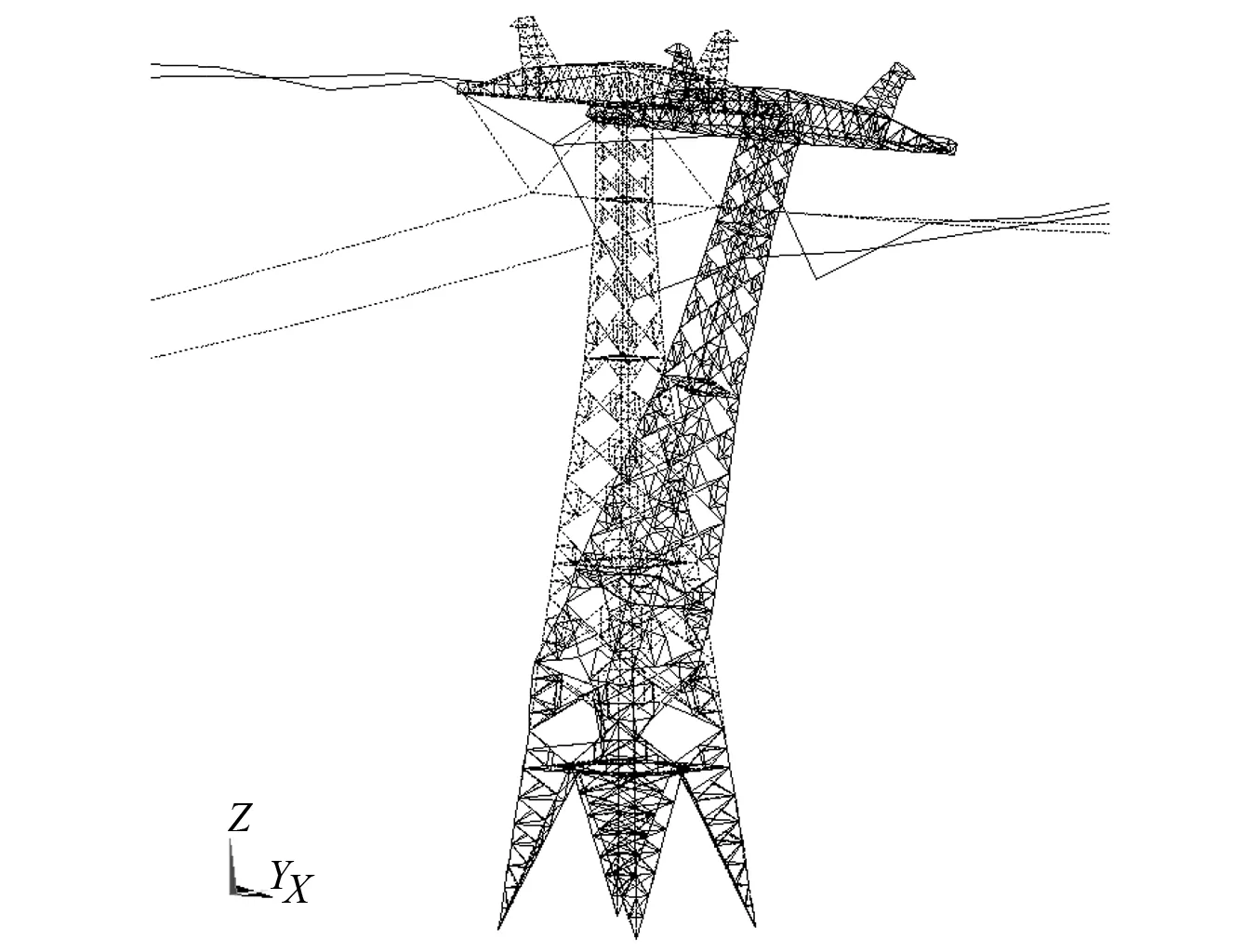
图20 输电塔线体系水平-摇摆耦合工况下失稳破坏特征图Fig.20 Instability failure characteristic diagram of transmission tower line-system under coupled horizontal-tilting ground motion

除Northridge地震记录外，中国台湾SMART-1台阵的地震记录提取的摇摆分量也能体现摇摆分量对结构体系的影响。限于篇幅，采用相同的方法选取SMART-1台阵中幅值较大的45号地震记录对模型进行计算，该地震记录的水平加速度时程曲线和转角位移时程曲线，如图21所示。经过计算对比单一水平地震作用，水平-摇摆耦合地震作用塔线体系动力失稳临界加速度峰值下降了19.8%，水平-竖向-摇摆耦合工况峰值下降了26.5%。基于以上分析，可以认为地震动摇摆分量的加入，会影响输电塔结构的动力稳定性，使其更易在地震作用下发生动力失稳破坏。

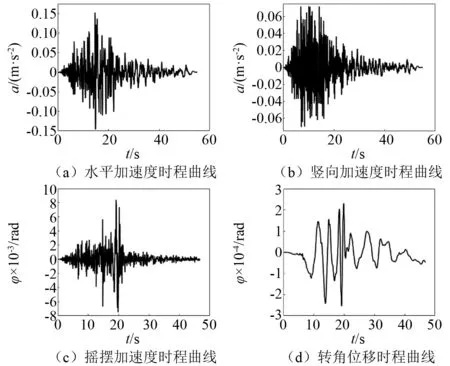
图21 SMART-1台阵地震的时程曲线Fig.21 Seismic time history curve of SMART-1

4 结 论

(1) 输电塔线体系在水平地震作用下具有较好的整体动力稳定性；考虑地震动摇摆分量作用后，会显著影响输电塔线体系动力稳定性能，水平-摇摆耦合地震作用下输电塔线体系动力失稳临界加速度相较单一水平工况明显减小，摇摆转角位移及其引起的附加P-Δ效应使输电塔线体系产生非对称振动，进而导致结构发生偏离平衡位置的单向变形，造成塔线体系更容易丧失整体稳定性能发生动力失稳破坏。

(2) 输电塔线体系在水平-竖向-摇摆耦合地震作用下，由于竖向地震作用导致P-Δ结构效应增大，使“重力二阶效应”变成“重力和竖向地震响应下共同的二阶效应”，将进一步放大摇摆分量对结构动力稳定性能的影响，加剧输电塔线体系动力失稳破坏。因此，探究高柔输电塔线体系在地震作用下的动力稳定性能时，除了考虑摇摆分量作用外，同时也不可忽略竖向分量的影响。

(3) 考虑摇摆地震作用影响后，输电塔线体系在水平-摇摆和水平-竖向-摇摆工况下发生动力失稳破坏，塔身呈现出上部位移大，变形小；而中下部位移小，变形大的特征。薄弱区域主要集中于塔身中下部，由于杆件失效使塔身局部变形过大，导致塔线体系发生整体动力失稳。因此，对输电塔线体系进行抗震设计时，应该适当增大塔身中下部薄弱区域杆件截面面积，提高结构整体承载能力和抗变形能力，以预防强震造成构件失效引发结构整体动力失稳。