磁悬浮轴承转子热弯曲振动特性研究

金超武， 董 岳， 苏 浩， 徐园平， 周 瑾， 闫 旭

(南京航空航天大学 机电学院，南京 210016)

磁悬浮轴承-转子系统因其无摩擦、无润滑、支承特性可调等特点，在旋转机械领域得到越来越多的应用。磁悬浮轴承工作时，由于铁损的集中会造成转子轴颈表面出现不均匀温度分布，进而引起热弯曲振动[1]。而热弯曲振动又会引起铁损集中程度的变化，进而形成一个闭环反馈，引起振幅与相位的不断波动，影响设备性能。事实上，此类由于转子轴颈温度分布引起热弯曲振动的现象在磁悬浮轴承之外的领域已被广大学者所知。由于定转子碰摩引起的热弯曲振动现象被称为Newkirk效应[2]，由于油膜黏性耗散引起的热弯曲振动现象被称为莫顿效应[3]。另外，此类现象对工作条件较为敏感，工作条件轻微的变化便会导致振动加剧或减小。此类现象目前仍未被工业界与学术界的专家所完全熟知。传统的转子动力学分析方法与设计标准通常无法排除与预测此类现象的影响。因此目前并没有普遍适用的方法或标准来预测、避免或排除旋转机械中热弯曲振动引起的不稳定性问题[4]。

针对这一问题，世界各国的学者做出了许多突破性的研究。Takahashi等[5]在磁悬浮离心压缩机中发现了不平衡振动螺旋形增加的问题，且认为铁损集中引起的热弯曲是此问题的原因，并建立了热弯曲振动的理论模型，讨论了其稳定性，同时利用试验获得了模型参数。Suh等[6-7]建立了可倾瓦轴承的热流体动力学模型，利用变黏度雷诺方程及三维能量方程得到了转子轴颈的温度分布，将转子的热弯曲变形等效成一系列不平衡力，并提出一种非线性瞬态计算方法得到了转子的热弯曲振动变化结果。另外还对转子和轴承结构进行了参数化分析，得到了各部分参数对热弯曲振动影响。Tong等[8-11]同样利用轴承的热流体动力学模型和非线性瞬态计算方法分析了转子的热弯曲振动现象及各部分参数的影响，另外通过试验验证了其模型和计算方法的正确性。Panara等[12-13]利用热-结构耦合模型和流体力学耦合模型，提出了一种新颖的迭代方法预测转子中的热不稳定性问题，并通过试验验证了其模型和方法的正确性。Yabui等[14]通过试验，将轴颈轴承看作PD控制器，利用轴颈温度和振动的试验数据，建立起基于频响的热弯曲振动模型及传递函数。由模型得到的振动特性与试验结果对应良好，证明了其模型的正确性。

针对磁悬浮轴承-转子系统中可能出现的热弯曲振动引起的不稳定性问题，本文利用Bertotti铁损分离模型得到转子轴颈处的铁损耗，建立起转子的热-结构耦合振动方程，以铁损耗作为热源，并结合磁悬浮轴承的支承特性，求解得到转子的热弯曲振动响应。同时，使用一种迭代计算的方法，不断更新振动幅值、生热率、温度分布和热变形，重复计算，直到振动收敛或发散。同时利用该方法分析了转子结构参数和电控参数对温度、温差及热弯曲变化的影响。计算的方法及结果可对预测、排除磁悬浮轴承-转子系统中热弯曲振动引起的不稳定性问题提供依据，也可在磁悬浮系统的结构设计、动力学设计及电控系统设计提供指导。

1 磁悬浮转子热弯曲振动变化规律

根据磁悬浮轴承的工作原理和工作特点，转子在工作时轴颈位置由于铁损集中出现温度分布，进而出现热弯曲和热弯曲振动。同时，热弯曲振动又会影响铁损集中的程度，从而形成一个闭环反馈，引起振动的波动和变化。

由于转子出现热变形的时间历程相对于转子的旋转周期来说相对较长，转子的热弯曲振动可视为准静态的过程。磁悬浮轴承转子的热弯曲振动变化规律如图1所示，具体过程为：

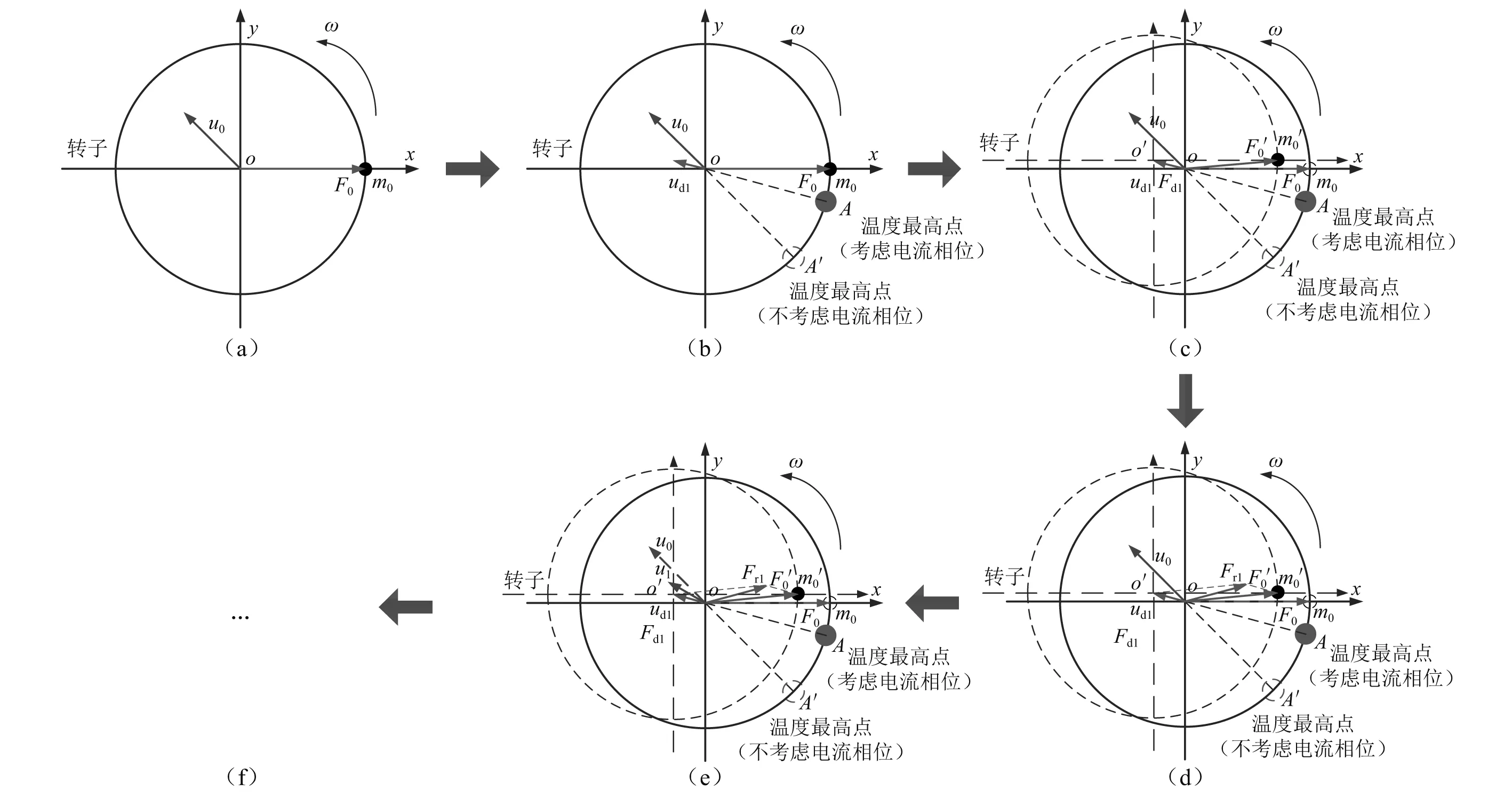
图1 磁悬浮轴承转子热弯曲振动变化示意图Fig.1 Schematic diagram of the thermal-bow vibration in magnetic suspension rotor

(1) 如图1(a)所示，假设转子存在不平衡质量m0，在转速ω下，m0产生的不平衡力F0引起转子的稳态振动位移为u0。

(2) 如图1(b)所示，根据磁悬浮轴承的工作原理，控制器在接收到位移传感器的位移信号之后，产生控制电流，控制电流产生电磁力将转子拉回平衡位置。又因为转子做同步涡动，控制电流产生的电磁力始终作用在间隙最大的位置，进而导致铁损集中，使转子圆周表面温度在A′位置(与位移方向呈180°)最高。事实上，控制电流相对振动位移会出现相位差，故实际温度最高点的位置在A点。由于轴颈温度分布，转子产生热弯曲ud1，与温度最高点呈180°(事实上，由于转子圆周表面的温度分布并不是严格的三角函数曲线形式，故热弯曲的方向也不是严格地在温度最高点的180°方向，但此处暂且认为是180°方向)。

(3) 如图1(c)所示，弯曲后的转子几何中心由旋转中心O变化至O′，产生不平衡力Fd1。同时不平衡质量由m0位置变化至m′0位置，其产生的不平衡力由F0变为F′0。

(4) 如图1(d)所示，出现热弯曲后的转子受不平衡力为Fd1和F′0的矢量和Fr1，与无热弯曲时的不平衡力在大小和方向上均有变化，故转子出现热弯曲后的振动位移ud1与无热弯曲时的振动位移u0相比，其振幅和相位也会发生变化，如图1(e)所示。

(5) 同理，热弯曲振动位移ud1又会引起温度分布、热变形的变化，产生新的振动位移。以此类推，故磁悬浮转子热弯曲振动的幅值和相位会不断波动和变化。

2 磁悬浮转子热弯曲振动迭代计算方法及计算模型

2.1 磁悬浮转子热弯曲振动迭代计算方法

针对磁悬浮轴承转子热弯曲振动的形成机理和变化规律，本文提出一种迭代计算的方法，通过结合磁悬浮轴承的支承特性和控制器特性，不断更新温度分布、热变形，得到磁悬浮转子热弯曲振动及其变化。磁悬浮转子热弯曲振动迭代计算流程如图2所示，具体步骤为：

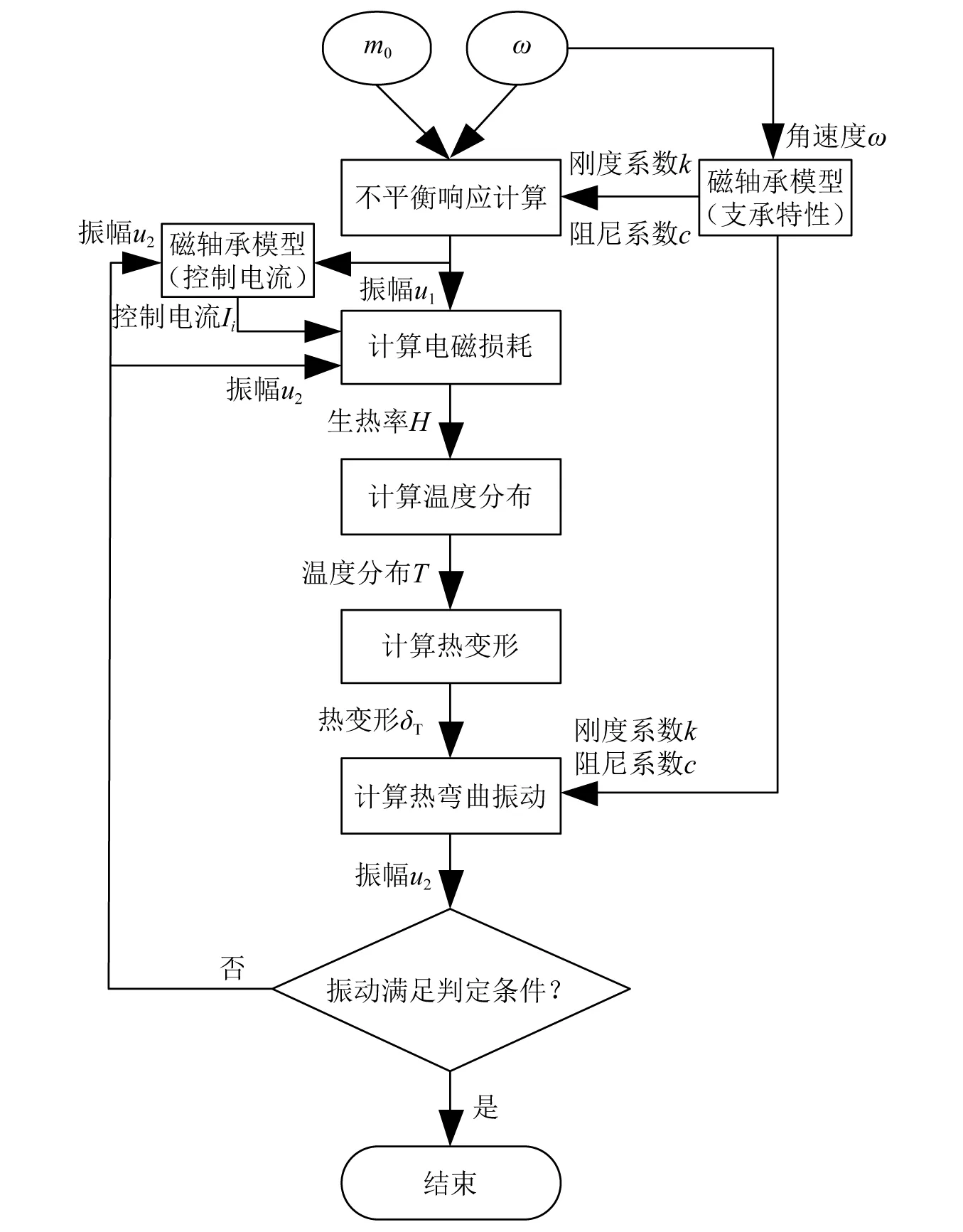
图2 磁悬浮转子热弯曲振动迭代计算流程图Fig.2 Flow diagram of iterative calculation method of thermal-bow vibration in magnetic suspension rotor

步骤1结合磁悬浮轴承的支承特性，求解转子在不平衡质量m0和转速ω下的不平衡响应；

步骤2利用轴承位置的不平衡响应，计算转子轴颈位置的铁损分布；

步骤3以转子轴颈铁损分布作为热源，求解转子温度分布；

步骤4利用转子温度分布，求解转子热变形；

步骤5结合转子温度分布和热变形，求解转子热弯曲振动；

步骤6以热弯曲振动作为条件，重复步骤2～步骤5，直到振动收敛或超过设定值。并在所有工作转速下重复该迭代过程，得到相应的热弯曲振动及变化过程。

2.2 各部分计算模型

2.2.1 磁悬浮轴承支承特性及控制电流

磁悬浮轴承工作时定子线圈内的电流包括偏置电流和控制电流，前者产生的电磁力抵消转子重力，后者产生的电磁力对转子进行控制，同时转子在电流产生的磁场中运动产生铁损。假设磁悬浮轴承控制规律的传递函数为

(1)

其频域表达式为

G(jω)=P(ω)+jQ(ω)

(2)

式中，P(ω)，Q(ω)分别为G(jω)的实部和虚部。根据磁悬浮轴承理论[15]，其等效刚度和等效阻尼为

(3)

式中，kx和ki分别为磁悬浮轴承的位移刚度和电流刚度，具体表达式为

(4)

式中：μ0为真空磁导率；S为单个磁极面积；N为线圈匝数；Ib为偏置电流；δ0为气隙大小。

磁悬浮轴承定子线圈中的电流包括偏置电流Ib和控制电流Ic，偏置电流根据磁悬浮轴承承载力确定，控制电流由电控系统和振动位移决定。控制电流的表达式为

Ic(s)=KsKAU(s)G(s)

(5)

式中：Ks，KA分别为位移传感器和功率放大器的增益；U(s)为转子振动位移的表达式。对式(5)做拉普拉斯逆变换可得控制电流时域表达式，故定子线圈中的电流为

Is=Ib+L-1[Ic(s)]

(6)

2.2.2 不平衡响应

转子的运动微分方程[16]为

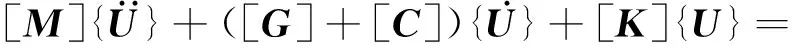
(7)

式中： [M]，[C]，[G]，[K]分别为转子的质量矩阵、阻尼矩阵、陀螺效应矩阵和刚度矩阵；Ω为转子转速；{Q}为转子所受广义力向量。

{Q}=[m1e1eiφ1, 0,m2e2eiφ2, 0, …,mNeNeiφN, 0]T

(8)

假设方程的特解为

{U}={A}eiΩt

(9)

代入原方程得

{A}=Ω2[-MΩ2+i(C+G)Ω+K]-1{Q}

(10)

则不平衡响应为

{U}=[a1eiε1, 0,a2eiε2, 0, …,aNeiε2N, 0]TeiΩt

(11)

2.2.3 电磁损耗模型

根据磁悬浮轴承理论，磁悬浮轴承气隙处的磁感应强度[17]为

(12)

式中：δ0为气隙长度；μ0为真空磁导率；φ为磁路总磁通量；Ap为磁极面积；N为线圈匝数；Is为线圈中的总电流。

磁悬浮轴承转子轴颈上的铁损耗按照产生机理分为磁滞损耗、涡流损耗和异常损耗，可分别表示为

Ph=∭f·Sdv

(13)

(14)

Pe≐ke(fB)1.5

(15)

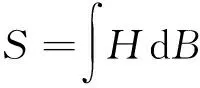
本文利用有限元软件计算转子轴颈处的铁损耗，软件利用软磁材料的各项损耗系数进行计算，故本文使用Bertotti铁损分离模型对试验测得数据进行拟合，得到硅钢片材料的各项损耗系数[18]。Bertotti铁损分离模型将铁损耗PFe按产生机理分为磁滞损耗Ph、涡流损耗Pc和异常损耗Pe，其关系为

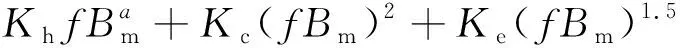
(16)

式中：Kh为磁滞损耗系数；a为磁滞损耗指数；Kc为涡流损耗系数；Ke为异常损耗系数；Bm，f分别为铁芯内磁感应强度幅值和磁感应强度变化频率。

2.2.4 转子热传导模型

根据传热学理论[19]，对于不可压缩的流体和固体，其导热微分方程为

(17)

式中：ρ为材料密度；c为比热容；qv为内热源的生成热；λx，λy，λz分别为x，y和z方向的导热系数。

对于磁悬浮轴承转子，其轴颈部件处的热边界条件，如图3所示。定转子气隙处硅钢片部件圆周面处的对流换热系数1通常取3～10 W/m2×℃[20]。对于硅钢片部件端面处的对流换热系数2和芯轴表面对流换热系数3可通过式(18)计算得到[21]

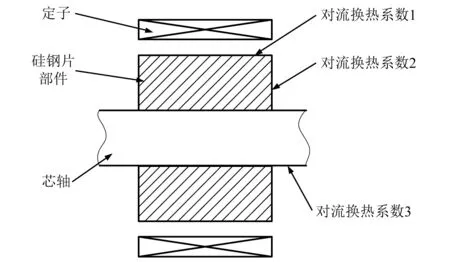
图3 转子轴颈部件热边界条件Fig.3 Thermal boundary condition of rotor journal

(18)

式中：n为转速；d为圆柱面直径。

2.2.5 转子热弯曲模型

转子轴颈出现不均匀温度分布时，其两侧受热膨胀不同，故出现热弯曲。转子热弯曲示意图如图4所示。对热弯曲进行合理的线性化，可推导出转子热弯曲的计算公式[22]。

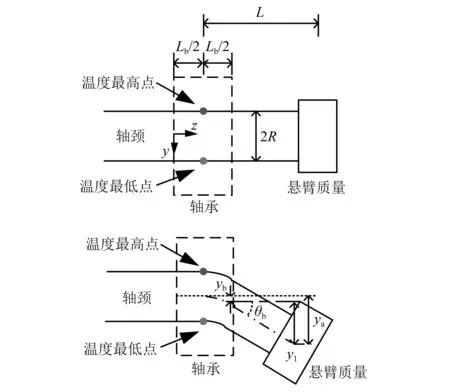
图4 转子热弯曲变形示意图Fig.4 Schematic diagram of rotor thermal deflection

根据材料力学基本理论，转子伸出位置总热变形为

(19)

式中：α为材料热膨胀系数；Lb为轴颈长度；R为轴颈位置半径； ΔT为轴颈温度差；L为从轴颈位置开始的伸出长度。

2.2.6 转子热-结构耦合振动方程

对于存在温度分布的转子，不均匀的膨胀受到约束而产生热应力，其基本方程为

(20)

式中：E(t)为随温度变化的弹性模量；α为线膨胀系数；T为转子工作时的温度；T0为初始环境温度；μ为泊松比。

根据达朗贝尔原理，有温度应力的转子振动方程[23]为

(21)

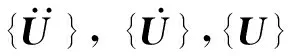
{P}=[m1(e1+yd1)eiφ1, 0,m2(e2+yd2)eiφ2, 0,…,
mN(eN+ydN)eiφN, 0]T

(22)

(23)

对于转子来说，任意位置的位移向量{U}由两部分组成

{U}={δ}+{δT}

(24)

式中： {δ}为原始形状到平衡位置的位移； {δT}为温度应力引起的变形。

3 磁悬浮转子热弯曲振动特性

本文以某型试验转子为例，利用上文提出的迭代计算方法计算其热弯曲振动及变化过程，并借此说明磁悬浮转子因轴颈铁损集中而产生的热弯曲振动的特点。试验定、转子基本结构如图5所示，转子由两个磁悬浮轴承支承，并由电机带动旋转。磁悬浮轴承控制规律选择PID控制。定、转子及电控系统基本参数，如表1所示。

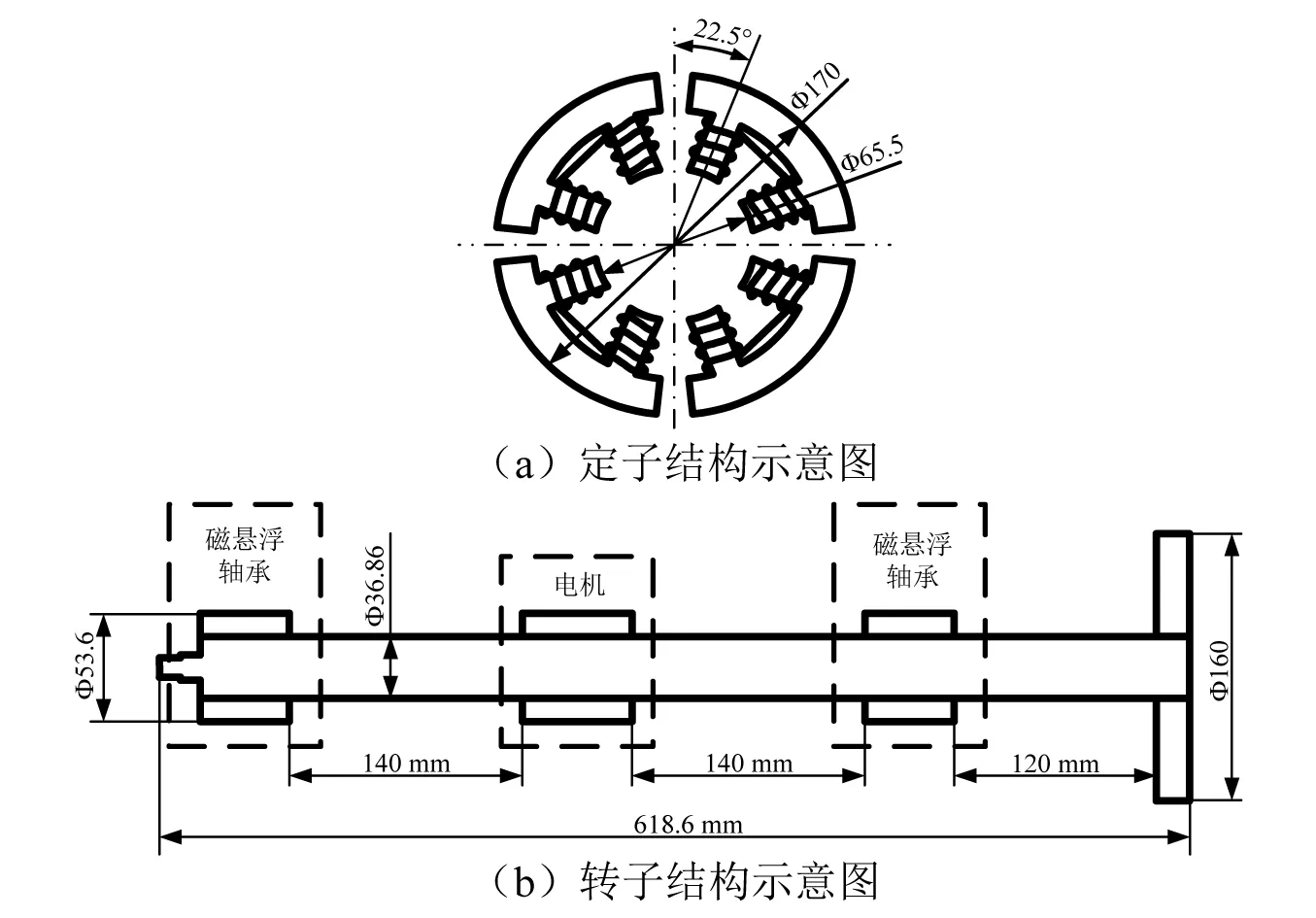
图5 定、转子结构示意图Fig.5 Structural diagram of the stator and the rotor

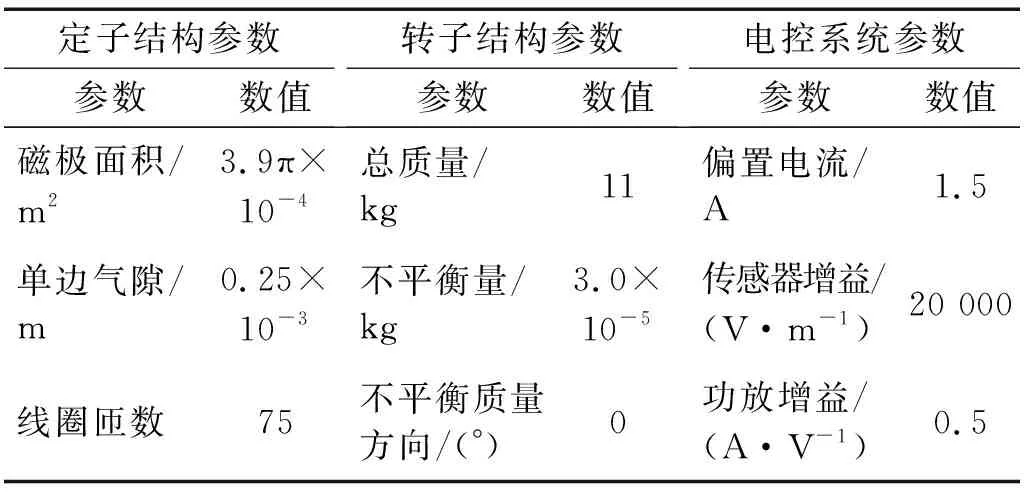
表1 定、转子结构参数及电控系统参数Tab.1 Parameters of the stator, the rotor and the control system

3.1 磁悬浮轴承支承特性及不平衡响应

PID控制规律下磁悬浮轴承电控系统的传递函数G(s)可表示为

(25)

式中：Kp，Ki，Kd分别为比例、积分、微分系数；Tf为不完全微分滤波器的截止周期；Ks和KA分别为位移传感器和功率放大器的增益系数。根据式(3)， PID控制策略下磁悬浮轴承的等效刚度和等效阻尼表达式为

(26)

式中，kx和ki分别为磁悬浮轴承的位移刚度和电流刚度。

结合磁悬浮轴承的支承特性，转子的坎贝尔图如图6所示。从图6中可知，转子的前两阶刚体临界转速分别为75 Hz和136 Hz，一阶弯曲临界转速约为354 Hz，对应的归一化振型如图7所示。

图6 转子坎贝尔图Fig.6 Campbell plot of the rotor

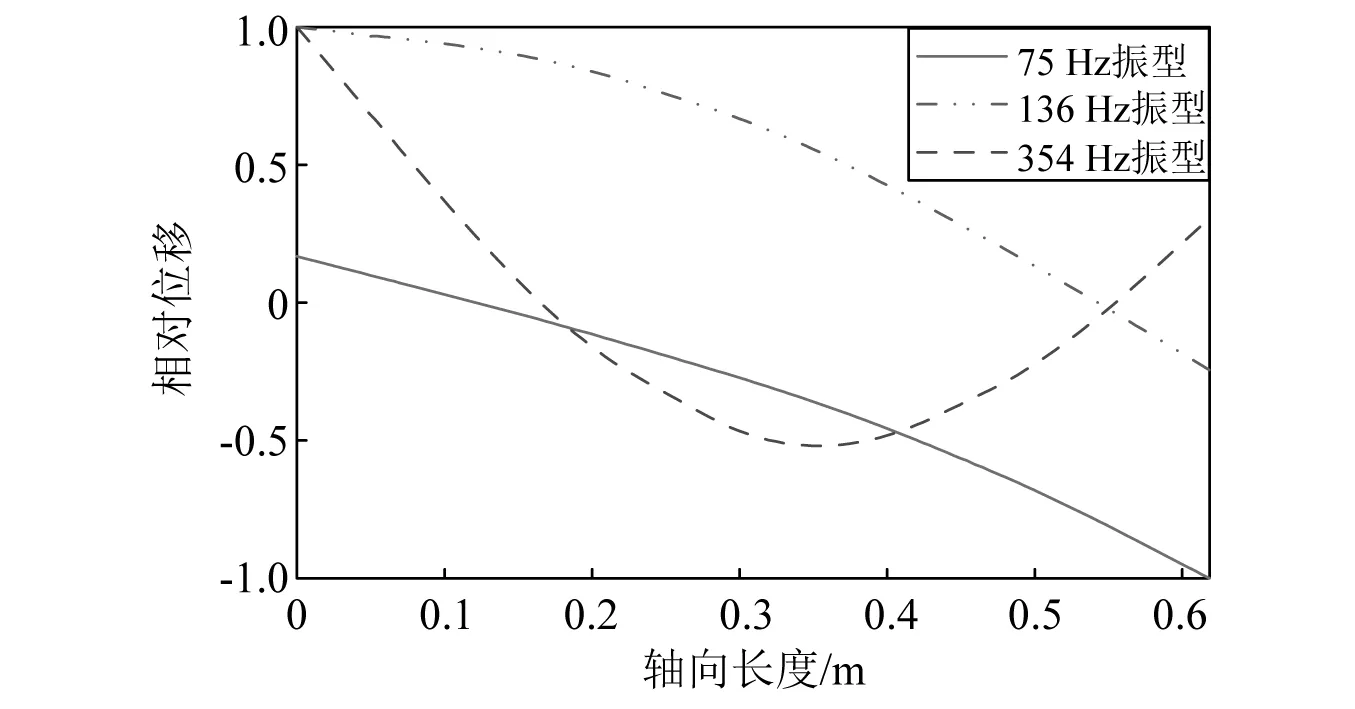
图7 转子振型图Fig.7 Modal shape of the rotor

本文利用有限元软件，结合等效刚度和等效阻尼，得到转子的不平衡响应如图8所示。

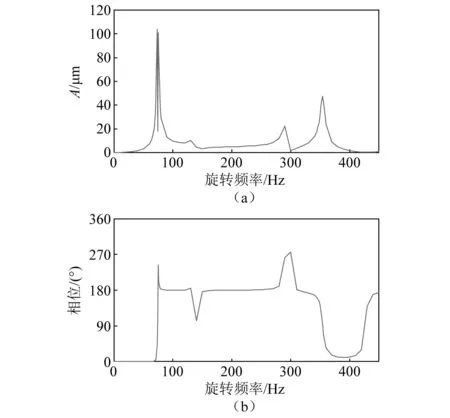
图8 磁悬浮转子不平衡响应Fig.8 Unbalance response of magnetic suspension rotor

3.2 转子铁损分布、温度分布及热变形

以70 Hz旋转频率为例，利用磁悬浮转子的不平衡响应，可得转子轴颈铁损分布。本文利用有限元软件，不平衡响应设置为偏心距，转速设置为与旋转频率相等，定子线圈内的电流根据式(6)设置，得转子轴颈横截面处的铁损分布，如图9所示。从图9中可以看出，由于转子在定子中做同步涡动，且控制电流始终跟随间隙最大的位置，轴颈横截面上的铁损出现了明显的集中。

图9 转子轴颈横截面铁损分布Fig.9 Iron loss distribution in the cross section of rotor journal

假设转子轴颈铁损分布在轴线方向不存在差异，即转子轴颈任意横截面的铁损分布一致，以铁损作为热源，可的转子的温度分布。本文使用有限元软件，根据铁损分布设置生热率作为载荷，设置环境温度为25 ℃，并按照式(18)设置图3中的相应边界条件得到转子的温度分布，如图10所示，转子轴颈圆周温度、温差分布，如图11所示。

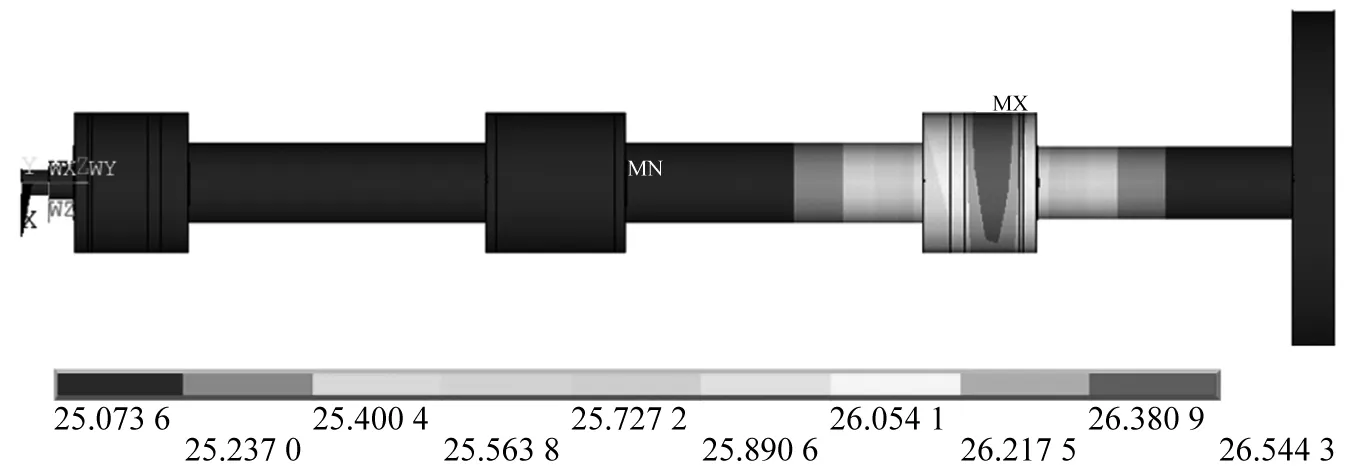
图10 转子温度分布Fig.10 Temperature distribution of the rotor

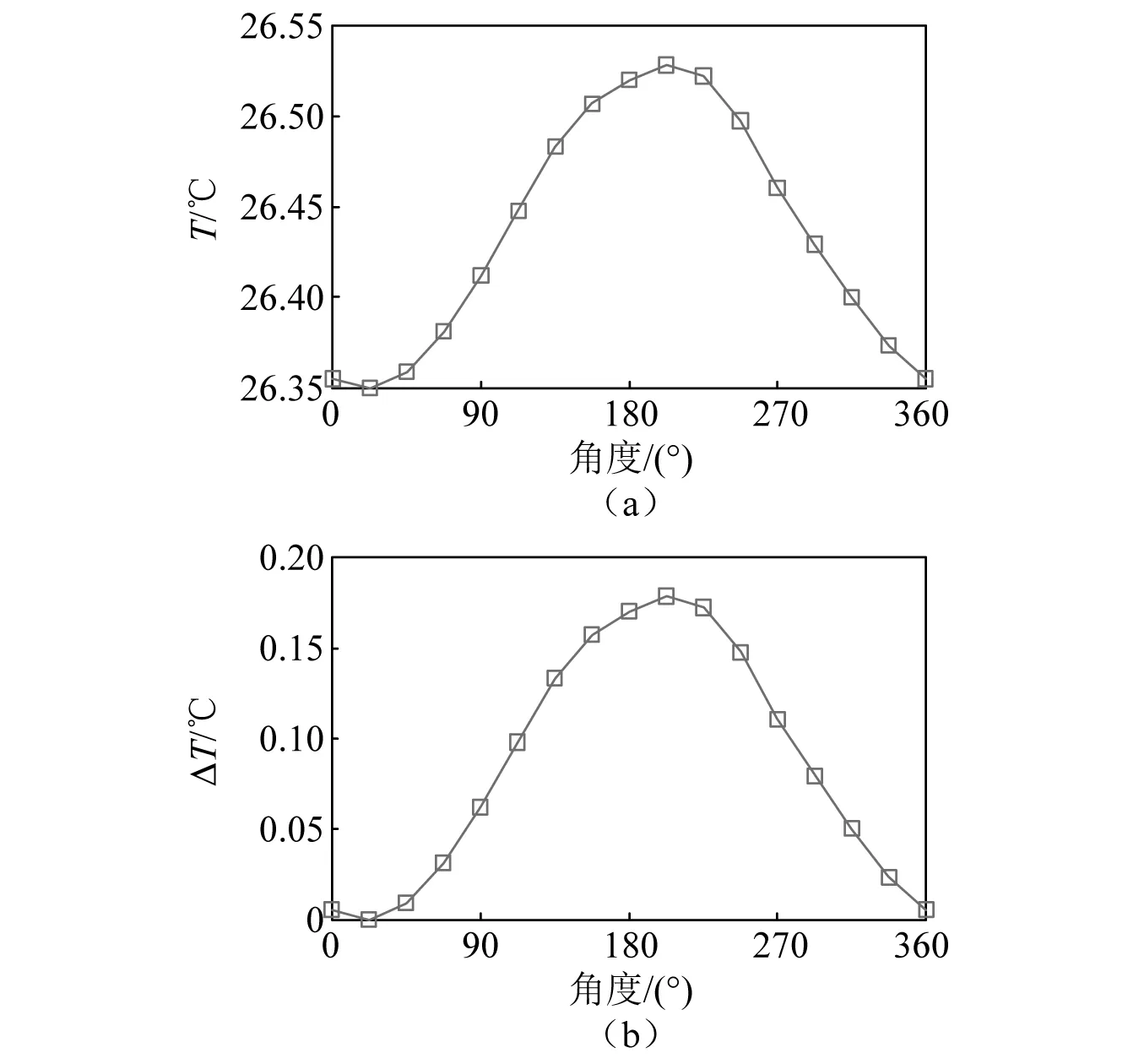
图11 70 Hz旋转频率下转子轴颈圆周温度、温差分布Fig.11 Temperature and temperature difference distribution in the rotor journal under 70 Hz rotation frequency

从图8、图9和图11可知，70 Hz旋转频率下转子靠近悬臂端磁轴承位置处的振幅为32.45 μm，方向3.174°，即此时在180°左右的位置轴承间隙最大。又因为转子在做同步正向涡动，控制电流产生的电磁力始终跟随间隙最大的位置，产生铁损集中，又由于控制电流存在相位差，故转子表面温度最高点出现在202.5°左右的位置。

利用转子温度分布，并认为转子左端完全约束，可得转子热变形如图12所示。从图12中可知，转子径向最大变形为0.252 μm，方向17.33°。热弯曲的方向基本与温度最高点位置呈180°(与振动方向基本同向)，但仍存在误差，其原因在于轴颈温度分布并不是严格的三角函数形式，即温度分布并不是严格对称的。

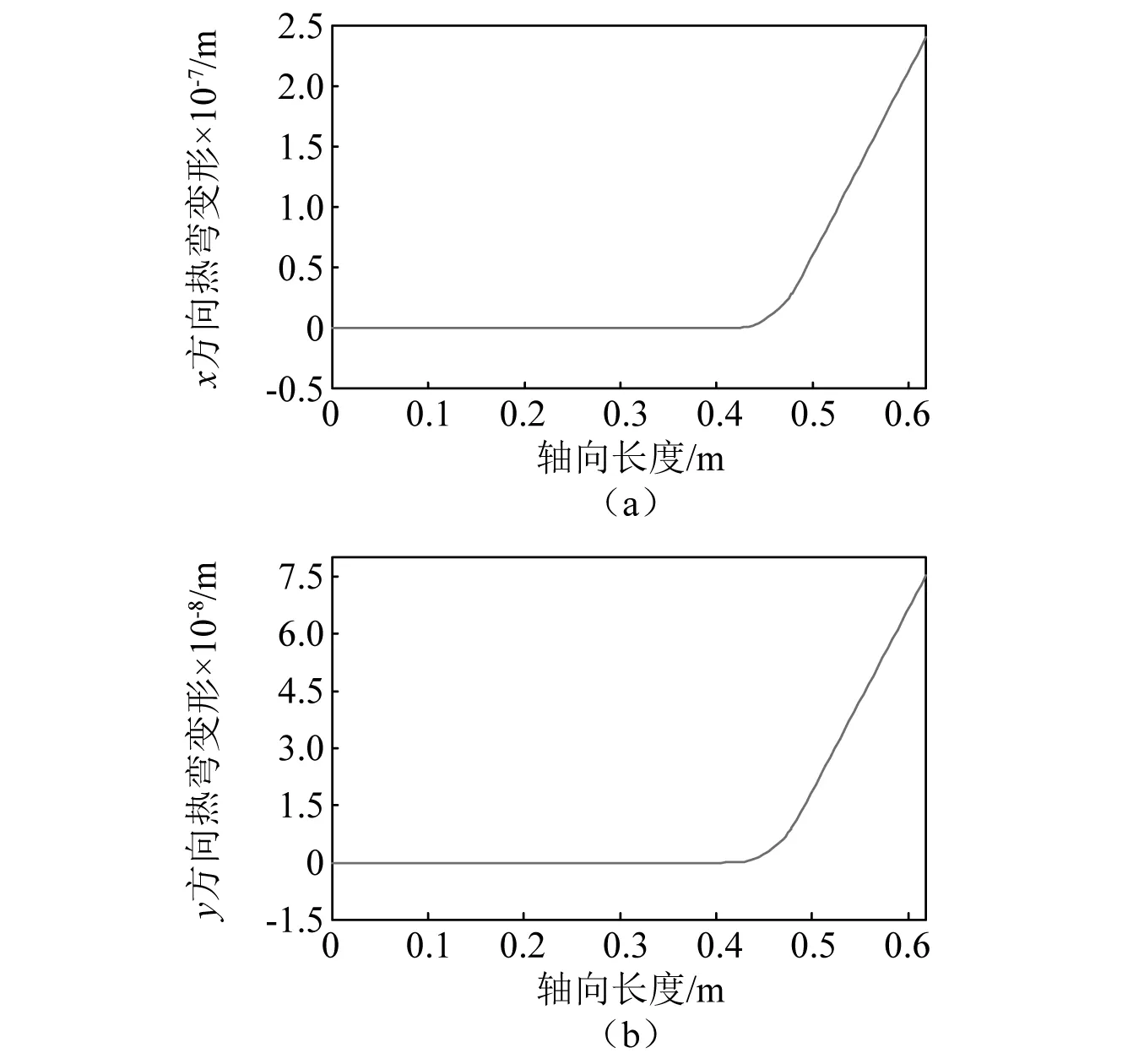
图12 转子x,y方向热弯曲变形Fig.12 Thermal bow deflection of the rotor in x and y direction

3.3 热弯曲-不平衡耦合振动及其变化

再利用热弯曲-不平衡耦合振动，求解得新的铁损分布、温度分布、热变形和热弯曲-不平衡响应，如此更新条件，重复迭代，直到振动收敛或超过设定值。由此获得转子轴颈圆周温度分布变化及热弯曲-不平衡耦合振动的变化过程，分别如图13(a)、图13(b)所示。

从图13中可以看出，70 Hz转速下转子的不平衡响应振动(图13(b)中第0次迭代)的方向为3.174°，铁损集中产生的温度最高点的方向为202.5°，产生的热弯曲方向为17.33°，即热弯曲产生的不平衡量方向在17.33°。此时热弯曲使残余不平衡质量远离旋转中心，且热弯曲产生的不平衡量与残余不平衡量之间呈锐角，故转子有热弯曲时受到的不平衡力的幅值比没有热弯曲时大，且相位也有一定变化，因此转子热弯曲-不平衡耦合振动与不平衡响应相比振幅变大，且相位也有一定变化。但由于振幅变化相对较小，并没有引起温度分布出现明显的、较大的变化(从图13(a)可知温差在0.18 ℃左右波动)，故出现热弯曲后的不平衡力未出现明显的变化，故振动收敛。

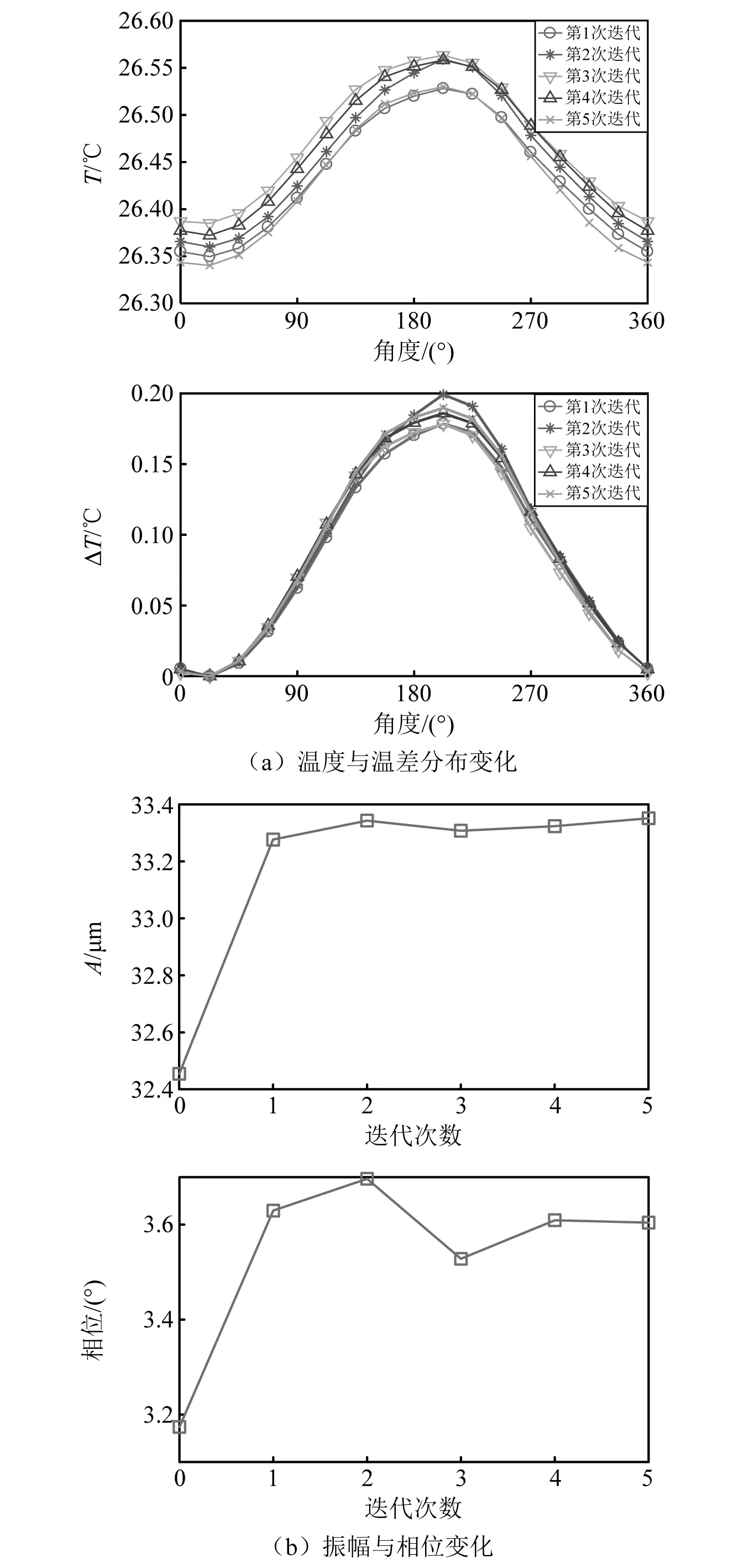
图13 70 Hz旋转频率转子温度分布及振动变化Fig.13 Temperature variation and vibration variation of the rotor under 70 Hz rotation frequency

3.4 不同转速下的热弯曲-不平衡耦合振动特性

由磁悬浮转子热弯曲振动的变化规律可知，转子振动位移的幅值、方向和旋转频率对热弯曲振动均有明显影响。从图8可知，试验转子在1～450 Hz旋转频率下不平衡响应的振幅和相位会出现明显的变化，故在1～450 Hz内计算转子的热弯曲-不平衡耦合振动及变化，并选择临界转速前后不平衡响应振幅、相位出现明显变化时，即50 Hz，70 Hz，80 Hz，200 Hz，350 Hz，360 Hz和400 Hz旋转频率说明振动变化的特点。

50 Hz旋转频率下转子轴颈温度分布变化和热弯曲-不平衡耦合振动变化，分别如图14(a)、图14(b)所示。从图14中可知，50 Hz旋转频率在转子的刚体临界转速之前，此时不平衡响应的振幅为3.2 μm，相位0.04°。由于振幅和旋转频率均较小，铁损总量和集中程度均较小，故整体温升和温差小。但可以看出温度在180°附近相对较高，故热弯曲使残余不平衡质量远离旋转中心，转子出现热弯曲时所受不平衡合力比无热弯曲时大，故热弯曲-不平衡耦合振动比不平衡响应振幅大，相位也出现一定变化，但振幅和相位变化均很小。

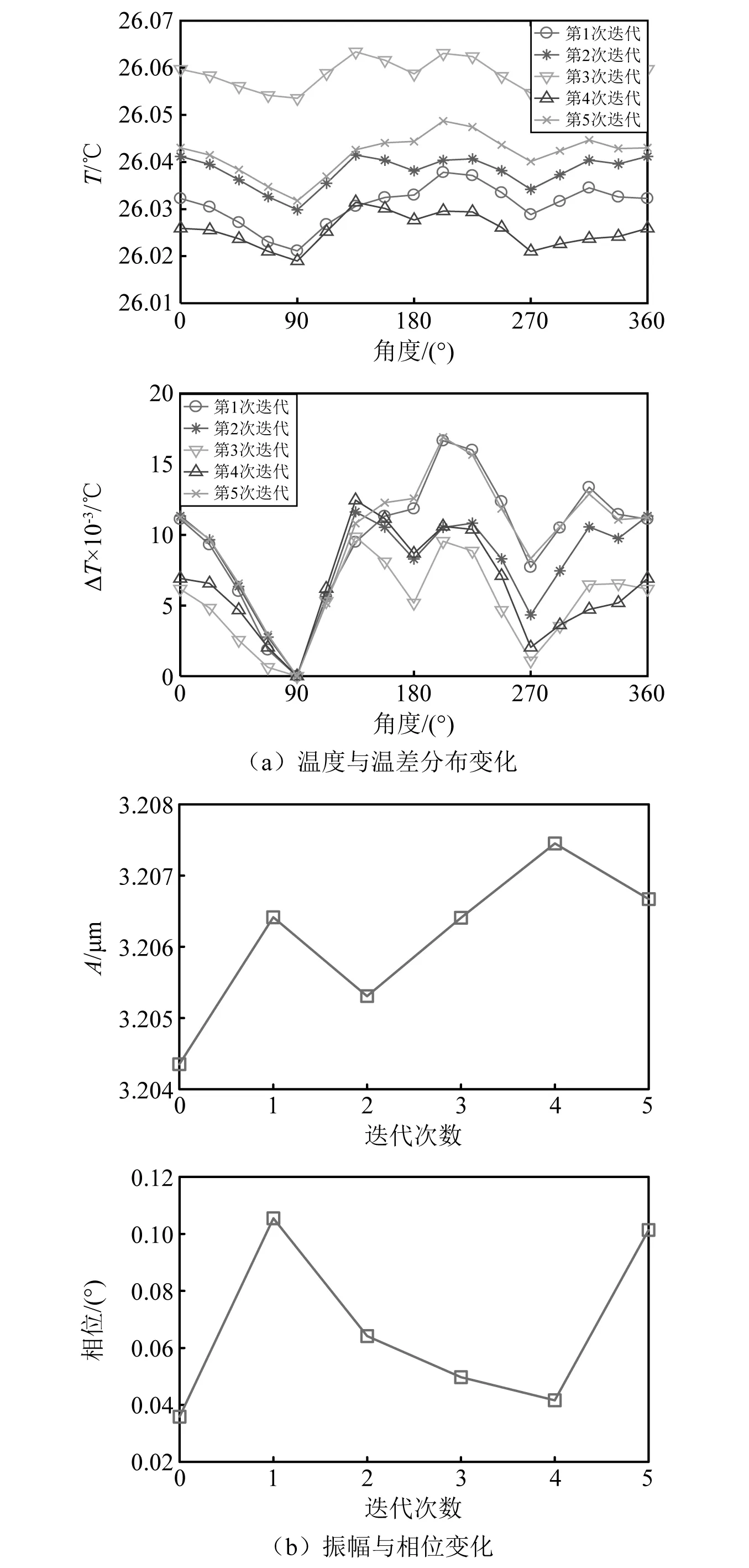
图14 50 Hz旋转频率温度分布及振动变化Fig.14 Temperature variation and vibration variation of the rotor under 50 Hz rotation frequency

70 Hz旋转频率下转子温度分布变化及振动变化已在上文中作出了分析，在此不作赘述。需要指出的是，70 Hz旋转频率接近转子的刚体临界转速，但仍在刚体临界转速之前，故不平衡响应的方向与不平衡质量的方向相近，此时热弯曲使残余不平衡质量远离旋转中心，出现热弯曲后的不平衡力相比无热弯曲时的不平衡力变大，故振动变大。但由于此时即使振幅相对较大，旋转频率相对较低，故振幅变化仍较小。

80 Hz旋转频率下转子温度分布变化和振动变化，分别如图15(a)、图15(b)所示。从图15中可知，由于80 Hz旋转频率刚刚超过刚体临界转速，故此时不平衡响应振动较大，约为28.8 μm。由于此时旋转频率已超过一阶刚体临界转速，振动相位为182°，铁损集中产生的温度最高点在22.5°左右位置，故热弯曲使不平衡质量更加靠近旋转中心，出现热弯曲时的不平衡力比无热弯曲时的不平衡力小，因此振动变小并逐渐稳定。

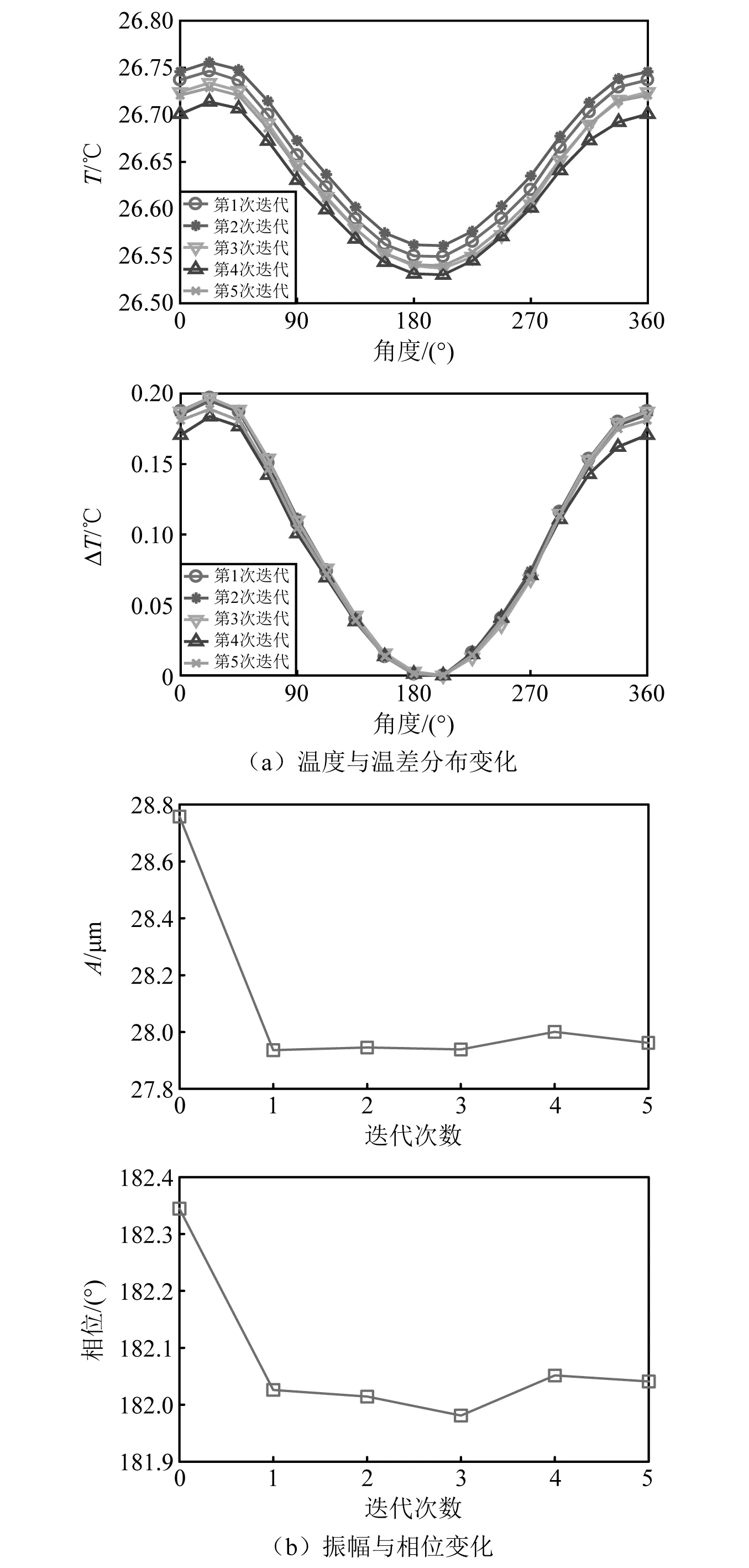
图15 80 Hz旋转频率温度分布及振动变化Fig.15 Temperature variation and vibration variation of the rotor under 80 Hz rotation frequency

200 Hz旋转频率下转子温度分布变化和振动变化，分别如图16(a)、图16(b)所示。此时旋转频率介于弯曲临界转速和刚体临界转速之间，不平衡响应的振幅为4.8 μm，相位180°。由于振幅较小，引起的温差较小，为0.14 ℃左右，且温度最高点在45°左右位置，但温度分布正弦性不好，故热弯曲使残余不平衡质量更加远离旋转中心，出现热弯曲后的不平衡力变大，故振动变小并稳定。

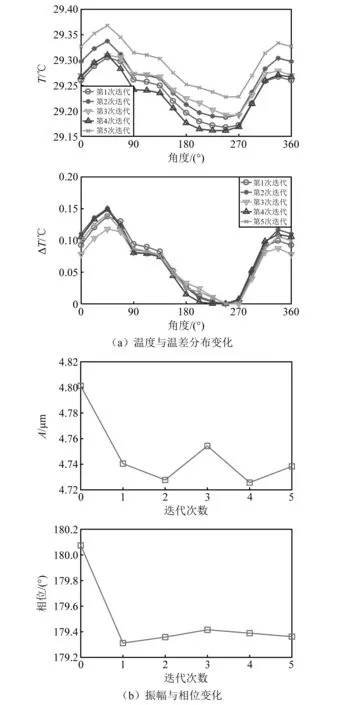
图16 200 Hz旋转频率温度分布及振动变化Fig.16 Temperature variation and vibration variation of the rotor under 200 Hz rotation frequency

350 Hz旋转频率下转子温度分布变化及振动变化，分别如图17(a)、图17(b)所示。从图17中可知，350 Hz旋转频率接近转子一阶弯曲临界转速，但在其之前，此时不平衡响应振幅较大，约为32 μm，相位约为140.9°。较大的振幅和较高的旋转频率使转子出现较大的温升，同时温度分布也较为明显，温差较大，约为2 ℃，温度最高点在0°左右位置，热弯曲使残余不平衡质量更加靠近旋转中心，出现热弯曲后的不平衡力比无热弯曲时明显减小，故振幅明显减小并逐渐稳定，同时相位波动较小。

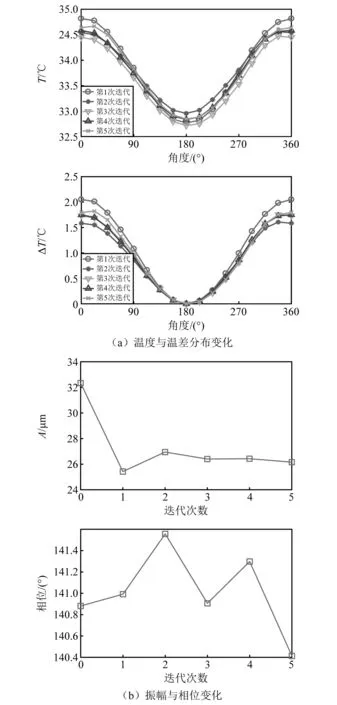
图17 350 Hz旋转频率温度分布及振动变化Fig.17 Temperature variation and vibration variation of the rotor under 350 Hz rotation frequency

360 Hz旋转频率下转子温度分布变化及振动变化，分别如图18(a)、图18(b)所示。从图18中可知，360 Hz旋转频率刚刚超过一阶弯曲临界转速，此时不平衡响应振幅相对较大，约为24 μm，相位约为35°。较大的振幅和较高的旋转频率使转子出现较大的温升，同时温度分布也较为明显，温差约为1.8 ℃，温度最高点在247.5°左右位置。此时热弯曲的方向与不平衡质量的方向夹角约为90°，故出现热弯曲后的不平衡力与无热弯曲时相比幅值变化不大，但角度变化相对较大，因此振动幅值变化较小，但相位变化相对较大。

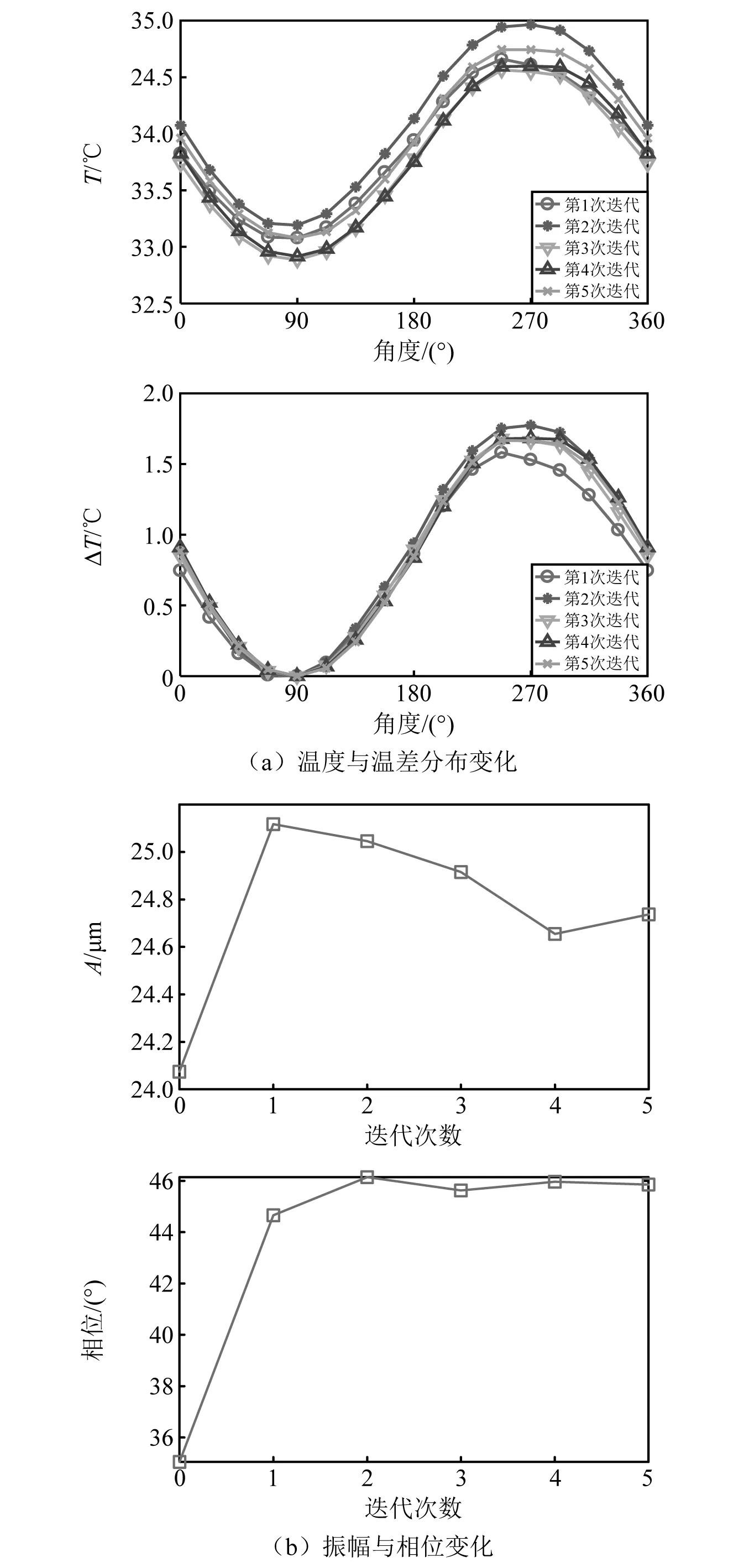
图18 360 Hz旋转频率温度分布及振动变化Fig.18 Temperature variation and vibration variation of the rotor under 360 Hz rotation frequency

400 Hz旋转频率下转子温度分布变化及振动变化，分别如图19(a)、图19(b)所示。从图19中可知，400 Hz旋转频率远离一阶弯曲临界转速，故不平衡响应的振幅较小。由于此时旋转频率较高，转子仍出现了明显的温升，整体温度约为34.8 ℃，但由于振幅较小，温度分布不明显，温差较小，约为0.25 ℃。因此振动变化很小，且变化趋势也不明显。

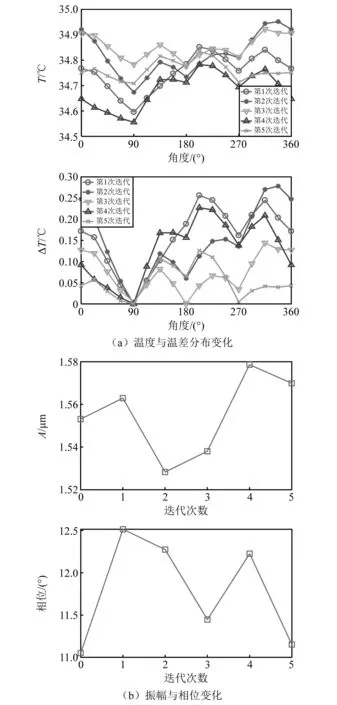
图19 400 Hz旋转频率温度分布及振动变化Fig.19 Temperature variation and vibration variation of the rotor under 400 Hz rotation frequency

1～450 Hz旋转频率转子最大温度、最大温差和不平衡响应相位与温度最高点的位置对比，分别如图20(a)、图20(b)和图21所示。从图20中可知，转子的整体温升、轴颈温差与旋转频率和振幅均有关，整体温升主要取决于旋转频率，且与旋转频率基本呈线性关系；而转子温差主要与振幅有关。从图21中可知，转子轴颈温度最高点的位置跟振动相位的关系基本为：温度最高点位置≈振动相位+180°+电流相位。

图20 最大温度、最大温差与旋转频率的关系Fig.20 Relationship between maximum temperature, Maximum temperature difference and rotational frequency

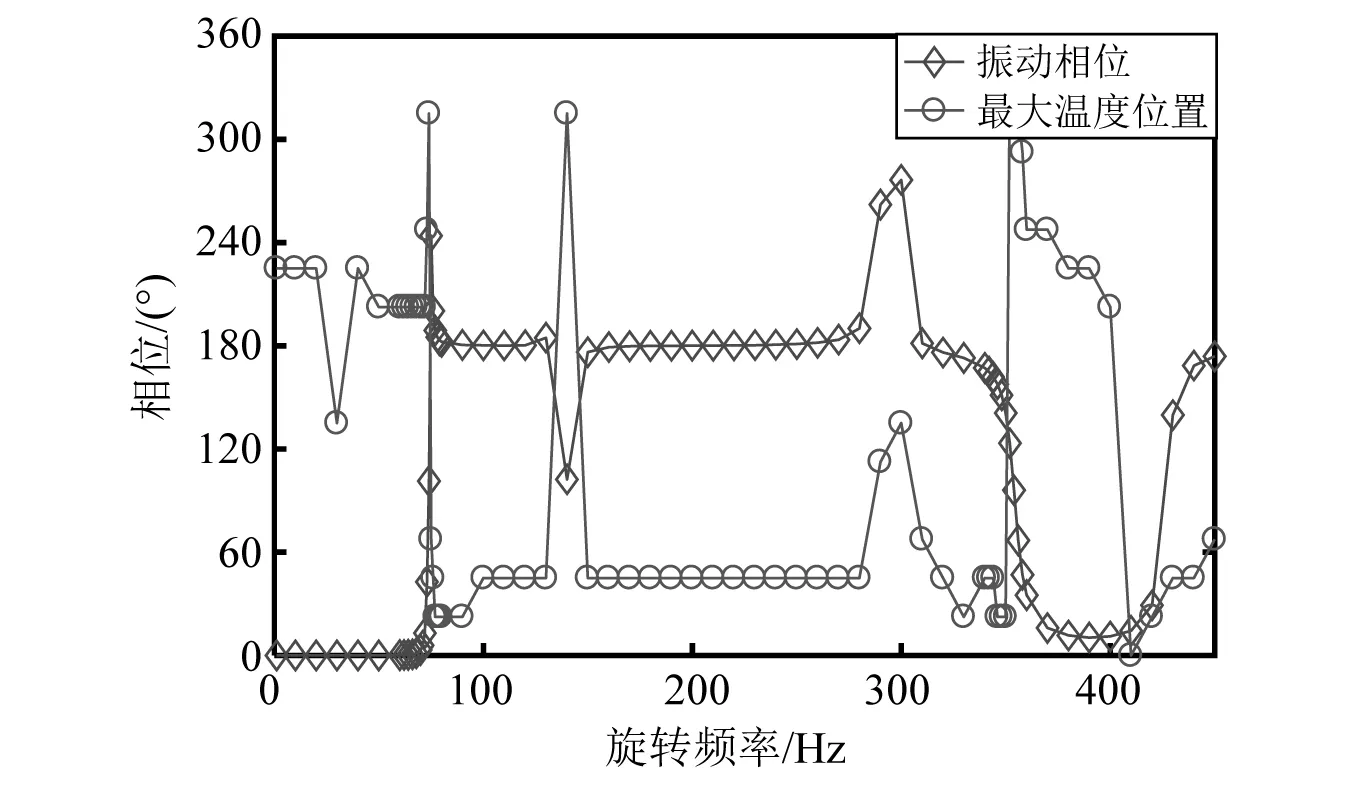
图21 最大温度位置与不平衡响应相位对比Fig.21 Phase comparison of the hot spot and the unbalance response

1～450 Hz旋转频率转子不平衡响应与热弯曲振动稳定值的对比，如图22所示。从图22中可知，本文研究的试验转子在接近临界转速时，由于振幅较大，铁损集中、温度分布较明显，才会出现一定的热弯曲振动。并且由于临界转速前后转子振动相位会出现明显的变化，故温度最高点的位置、弯曲方向会出现明显变化，进而导致热弯曲振动比不平衡响应大或小。而远离临界转速时，由于转子振幅较小，铁损集中、温度分布不明显，产生的热弯曲振动可忽略不计。又由于本文研究的试验转子在出现热弯曲振动时振动变化不大，故可认为热弯曲振动不会对系统产生明显影响。

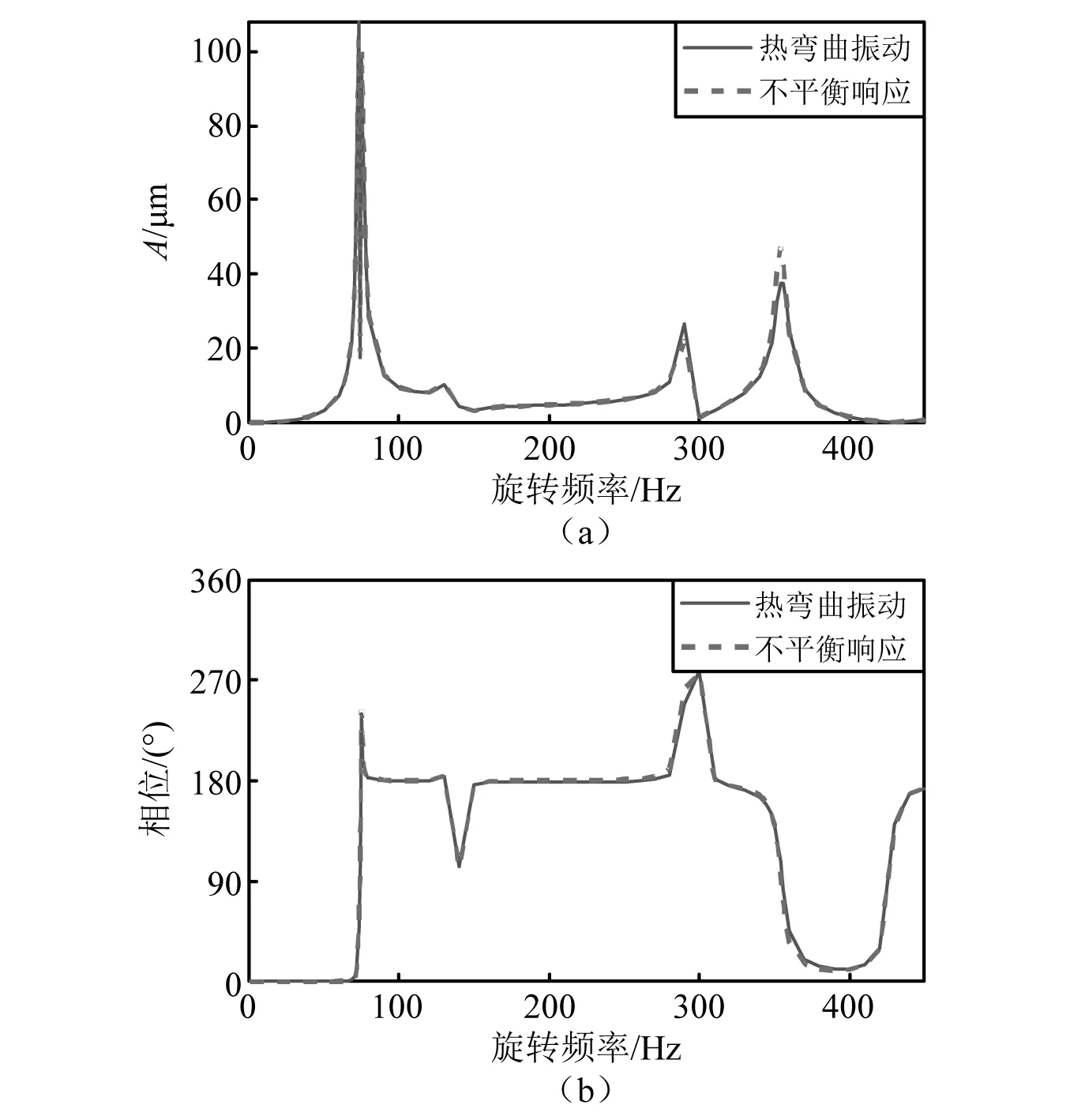
图22 热弯曲-不平衡耦合振动与不平衡响应对比Fig.22 Comparison between thermal-bow-unbalance coupled vibration and unbalance response

4 结 论

本文研究了磁悬浮轴承转子因轴颈铁损集中产生温度分布而出现的热弯曲振动的变化规律。并以振动引起的铁损分布作为热源，得到转子温度分布、热变形及热弯曲-不平衡耦合振动，同时不断更新条件，迭代计算，直到振动收敛，由此得到并分析磁悬浮轴承转子热弯曲-不平衡耦合振动变化过程，结论如下：

(1) 磁悬浮轴承转子轴颈温度分布与转子振幅和旋转频率有关。其中，转子整体温升主要取决于旋转频率，而轴颈温差主要跟振幅有关。

(2) 磁悬浮轴承转子轴颈温度最高点的位置，即热弯曲的方向主要跟振动方向有关，二者之间的关系为——温度最高点位置≈振动相位+180°+控制电流相位。

(3) 磁悬浮轴承转子热弯曲方向决定着转子出现热弯曲后所受不平衡力相比无热弯曲时不平衡力幅值和相位的变化，即无热弯曲时的振动方向决定着出现热弯曲后振动幅值和相位的变化。

(4) 针对本文研究的试验转子及电控系统，由于振动引起温度变化较小，故转子所受不平衡力变化小，故热弯曲振动会逐渐趋于稳定，可认为热弯曲振动对系统影响较小。