双机驱动双质体振动机械系统的同步及其稳定性

李振民， 张学良， 岳红亮， 闻邦椿

(东北大学 机械工程与自动化学院，沈阳 110819)

磨机在工业中已有几十年应用历史，近年来，对球磨机磨削技术的研究引起了广泛关注[1-2]。由于具有高效、节能的特点，根据自同步理论设计的振动球磨机具有较大应用潜力。

荷兰物理学家Huygens最早发现同步现象。此后，Blekhman[3]解释了双偏心转子机械系统的同步机制，并给出同步定义。Wen等[4]采用平均法，对两相同激振器同步理论推导过程进行简化，设计出多种双机自同步驱动机构，并将同步理论应用到工程，开创了振动利用工程学科。基于改进小参数法，Zhao等[5]研究了空间运动机械系统中激振器的同步。根据庞加莱法和中心流形定理，侯勇俊等[6]推导出旋转振动筛系统的同步性和稳定性判据。利用平均法和Lyapunov原理，陈帮等[7]研究了超共振转子系统的耦合机理。Fang等[8]讨论了激振器和摆耦合振动系统中的同步现象。基于Routh-Hurwitz判据，陈晓哲等[9]给出两激振器共旋转轴线振动系统中激振器同步运动的稳定性条件。近年来，控制同步和复合同步也得到关注： Jia等[10]对同向回转双偏心转子倍频控制同步进行了研究； Kong等[11]分析了四机驱动单质体系统的复合同步问题。

一般在工程中，根据外部运转频率与固有频率的比值(以z表示)，系统的共振类型分为四种：亚共振(z<0.9)、亚近共振(0.91.1)。对于过共振类型，当外部运转频率远大于固有频率时(一般z>2)，又被称为超远共振。

文献[12]将同步理论应用于碎磨领域，在考虑质体空腔中滚子干摩擦条件下，研究超远共振双机驱动振动系统中圆柱滚子的振动同步传动机理。

根据上述文献，由于结构简单，理论推导相对容易，单质体系统同步理论得到了充分研究。但在工程中，对于球磨机等碎磨设备，常需利用质体间相对圆周运动实现工程所需机器的特定功能。因此，有必要对双质体系统同步理论进行研究，特别需要针对其同步机理、相对运动特性和系统理想工作区域等问题，进行详细剖析。

本文采用弹簧将一个圆柱体与质体内的空腔相连，以替代Zhang等研究中的滚子。把圆柱体视作有弹性耦合的内部自由度，研究双机驱动双质体振动机械系统的同步及其稳定性问题。区别于Zhang等的研究仅考虑超远共振，本文在现有研究基础上进行扩展和创新，考虑多个共振区域内运动特性。通过平均法和Hamilton原理推导出系统实现同步运行和保证同步状态稳定性的理论判据。基于数值定性分析，研究系统同步稳定区域和相对运动幅频特性。最后通过仿真，验证理论方法的有效性。研究结果可为振动磨机的设计提供理论参考。

1 系统动力学模型和运动微分方程

图1为系统的动力学模型和参考坐标系，由两个子系统组成，即主振系统和隔振系统。主振系统包括主振质体1(m1)和主振弹簧k1，隔振系统包括隔振质体2(m2)和隔振弹簧k2。质体2分别通过隔振弹簧k2和主振弹簧k1与基础和质体1相连，质体1位于质体2的空腔内部质心处，可以认为是系统的一个内部自由度。由两个同向回转交流电机分别驱动的一对激振器对称安装在质体2两端，且均沿逆时针方向旋转。图1(a)中，o点为主振质体质心，同时也是系统坐标原点。系统的参考坐标系如图1(b)所示，包括固定坐标系oxy、移动坐标系o′x′y′和旋转坐标系o′x″y″。

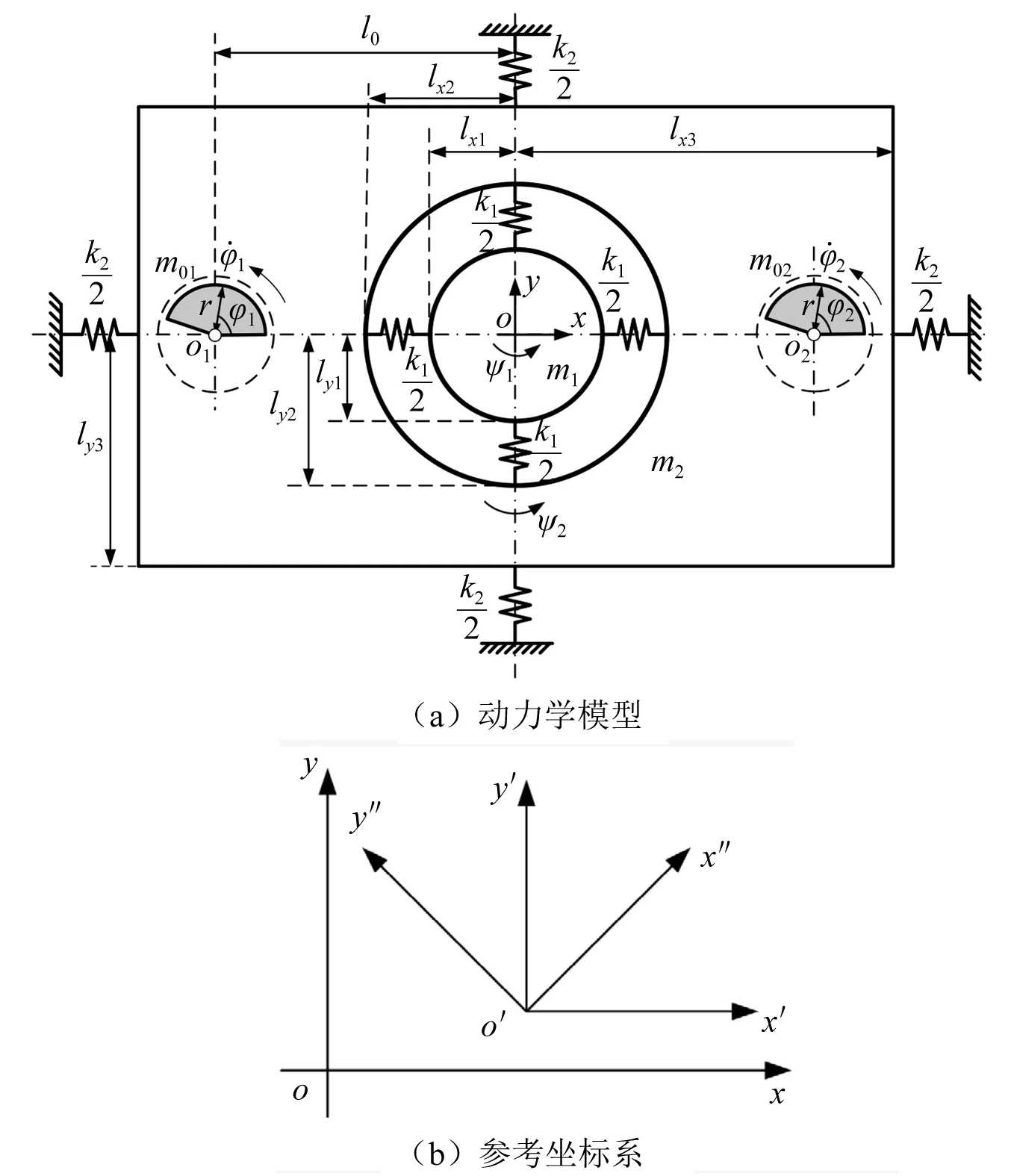
图1 双机驱动双质体振动机械系统的动力学模型和参考坐标系Fig.1 Dynamical model and reference coordinate system of the vibrating mechanical system with double rigid frames driven by two vibrators

为实现机器预期功能，需对系统同步机理及其稳定性进行揭示，在研究过程中，本文采用以下参数设定和模型假设：①选取两相同激振器以实现较好的同步效果，即激振器质量m01=m02=m0，且回转半径相等；②假设两激振器的平均相位为φ，相位差为2α，即φ1-φ2=2α，φ1+φ2=2φ，解得φ1=φ+α和φ2=φ-α；③因为系统的运动具有周期性，故电机的角速度周期性变化，在两电机最小正周期内，其平均角速度的平均值应为常数，以ωm0表示。

系统共有六个运动自由度，即x1，y1，ψ1和x2，y2，ψ2，分别表示两质体在x，y和ψ方向的运动位移。此外，两激振器分别绕自身回转轴旋转，以φ1和φ2表示。选取q=[x1，y1，ψ1，x2，y2，ψ2，φ1，φ2]T为广义坐标(反映绝对运动特性)，并以x12=x1-x2，y12=y1-y2，ψ12=ψ1-ψ2分别表示两质体在x，y和ψ方向的相对运动位移(反映相对运动特性)，基于拉格朗日方程，求得系统运动微分方程为

(1)

其中，

式中：r和m0分别为激振器的回转半径和质量；M1和M2分别为主振质体和隔振质体(包括电机及偏心块)的质量；J1和J2分别为主振系统和隔振系统的惯性力矩；Jm2为质体2惯性力矩；l0为激振器旋转中心与系统质心o点间距离；le为系统关于质心的等效回转半径；J0为电机惯性力矩；M和J分别为系统的总质量和总惯性力矩；fd1和fd2为电机1和电机2的轴摩擦因数；Te1和Te2为两电机电磁转矩；k1，k2，kψ1和kψ2为弹簧刚度；f01，f02，fψ1，fψ2和fψ12为阻尼系数，在工程中，一般fψ1≈fψ2≈fψ12；lx1，lx2，ly1和ly2为主振弹簧k1在水平和竖直方向的安装尺寸；lx3和ly3为隔振质体尺寸参数；rl为无量纲参数。

2 系统同步稳定运行的理论判据

2.1 系统响应求解

基于传递函数法及叠加定理[13]，两质体在x，y和ψ方向的绝对运动响应为

(2)

其中，

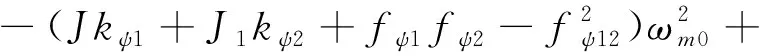
b2=[kψ1(fψ1+fψ2-2fψ12)+kψ2fψ1]ωm0-

χAi=b1ci-a1d1，χBi=a1ci+b1d1，

χCi=b2ei-a2gi，χDi=a2ei+b2gi，i=1，2。

将式(1)中前四个方程按顺序标记为①②③④，并执行如下运算：(①×M2-②×M1)/M和(③×M2-④×M1)/M。得到系统在x和y方向的相对运动微分方程

(3)

其中，

式(3)中两个方程分别含有关于x2和y2的耦合项，这给求解相对运动x12和y12的响应带来困难。文献[14]中的解决方法是直接忽略数值较小的阻尼参数f02和刚度参数k2，使式(3)转化为仅关于x12或y12的线性微分方程。为提高求解精度，本文在不忽略f02和k2的前提下求解相对运动响应。

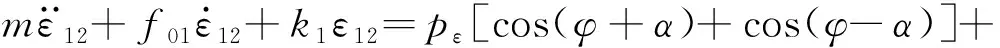
(4)

其中，

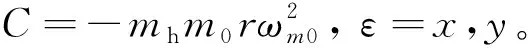
基于式(4)可求得系统固有频率和相对运动响应，分别以ωn和ε12表示

(5)

其中，

将式(5)中三角函数展开，并整理展开后的表达式，求得

ε12=λsεcosφ+λcεsinφ=λεsin(φ+γε)

(6)

其中，

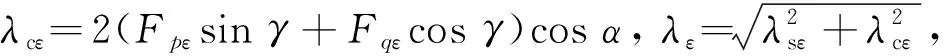
式中：λx和λy为x和y方向的相对运动振幅，将在数值分析环节进一步讨论；γx和γy为两质体间相对运动滞后角。

2.2 系统同步性判据

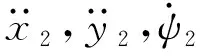
Te01-df1-fd1ωm0=0，Te02-df2-fd2ωm0=0

(7)

其中，

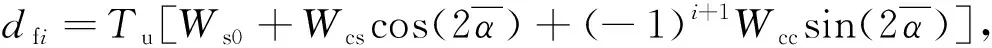
式中：Te01和Te02为两电机在平均角速度ωm0时的电磁转矩；df1和df2分别为振动系统施加在电机1和电机2上的负载力矩；Wcc被称作余弦耦合系数；Tu为激振器动能。

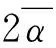
(8)

式中，TD=(Te01-fd1ωm0)-(Te02-fd2ωm0)为两电机有效电磁输出转矩之差；TC=2TuWcc为系统频率俘获力矩。

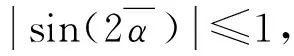
2.3 系统稳定性判据

(9)

单周期内Hamilton平均作用量I为

(10)

(11)

其中，

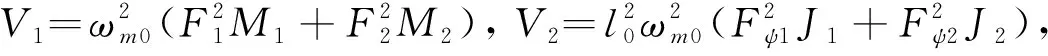
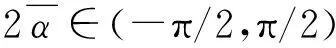
3 数值定性分析

为进一步揭示系统动态特性，基于理论研究结果，本章定性给出一些数值分析。系统参数设定为：k1=9 000 kN/m，kψ1=7 200 kN/rad，k2=150 kN/m，m0=20 kg，kψ2=120 kN/rad，m1=350 kg，m2=1 600 kg，J1=50 kg·m2，Jm2=1 200 kg·m2，f01=f02=3.83 kN·s/m，fψ1=fψ2=fψ12=f01，r=0.15 m。根据上述参数，基于式(5)求得系统固有频率为ωn≈176.7 rad/s。

两电机规格相同，均为三相鼠笼式异步电机，参数为：50 Hz，380 V，6极，0.75 kW，额定转速980 r/min，转子电阻Rr=3.4 Ω，定子电阻Rs=3.35 Ω，定子互感Lm=164 mH，转子电感Lr=170 mH，定子电感Ls=170 mH，电机轴摩擦因数fd1=fd2=0.005。

考虑到激振器安装位置可能会对系统的同步和稳定性产生影响，研究了rl-ωm0平面内系统同步稳定区域，如图2所示。rl为无量纲参数，表示激振器旋转中心和系统质心间距离l0与系统等效旋转半径le的比值。

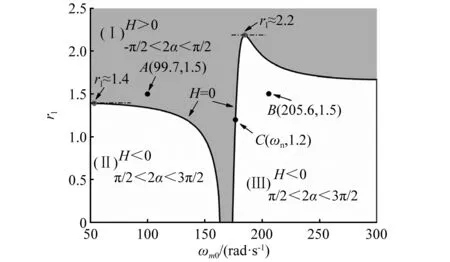
图2 rl-ωm0平面内系统同步稳定区域Fig.2 Synchronous and stable regions under the rl-ωm0 plane

由图2，rl-ωm0平面以H=0为分界线被分为三个区域。在区域Ⅰ(灰色区域)，稳定能力系数H>0，两电机相位差满足-π/2<2α<π/2。对于两相同激振器，相位差2α稳定在0°，如图3所示。在区域Ⅱ和区域Ⅲ(白色区域)，H<0且π/2<2α<3π/2，此时两相同激振器的稳定相位差为180°。在这种情况下，两激振器产生的激振力相互抵消，系统几乎无振动或仅有很小的摆动。从应用角度，仅区域Ⅰ的相位差状态满足工程需要。

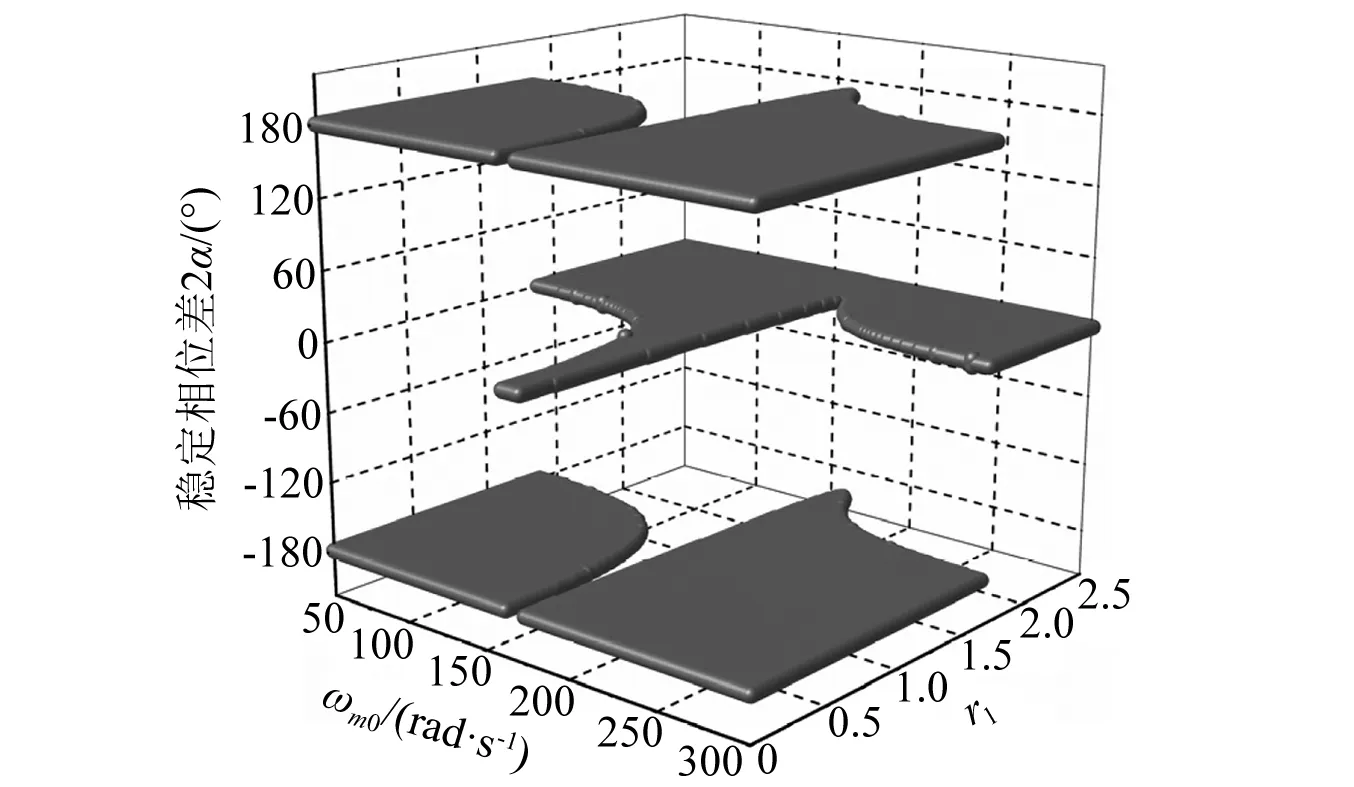
图3 稳定相位差(两相同激振器)Fig.3 Stable phase difference for two identical vibrators

振动机械的最终功能通常反映在相位差和机体振幅。以rl=1.5为例，基于式(6)，并在图2中相位差分布数值结果的基础上，进一步得到两质体间相对运动振幅随ωm0变化的曲线，如图4所示。由于实际工程中机器摆角一般非常小，因此只考虑了x和y方向的相对运动。且经计算，式(6)中λx=λy。

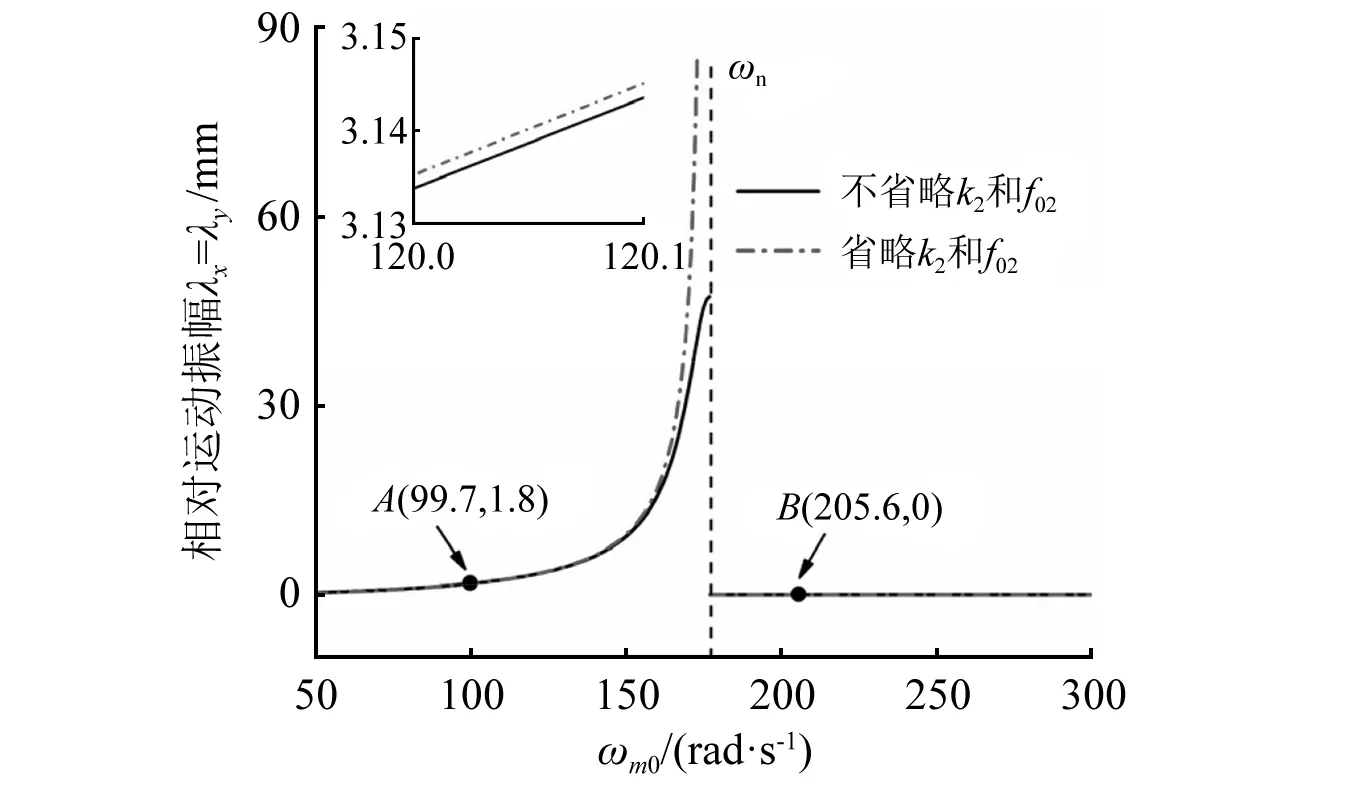
图4 相对运动幅频特性曲线(rl=1.5)Fig.4 Frequency-amplitude curve of the relative motion for rl=1.5

由图4可知，随着ωm0增大，相对运动振幅持续变大，直到在ωn的亚近共振区域达到峰值。当继续增大ωm0通过共振点后，曲线出现断点，λx和λy的值迅速跌落到0，这是因为在亚过共振和过共振区域，两激振器的相位差为π。此外，当远离共振点时，是否忽略f02和k2对λx和λy的值影响不大。但在共振点附近，特别是在ωn的亚近共振区，省略f02和k2会导致相对运动振幅远大于实际值。相比2019年Zhang等的研究，本文求解相对运动振幅的方法精度更高。

根据以上分析，为满足工程需要，首先应将工作点选定在图2中区域I，然后进一步调整ωm0的值，使其落在ωn的亚共振或亚近共振区域。在该种参数匹配下，两激振器相位差稳定在0°，两质体间主要运动形式为相对圆周运动，且隔振效果较好，见仿真环节图5(f)。这些特征符合工程上对振动球磨机的工作要求。

4 仿 真

为检验理论方法的有效性，将Runge-Kutta程序应用于系统运动微分方程式(1)，对系统进行A和B两组仿真，结果如图5所示。仿真中l0=1.2 m，le=0.8 m，即rl=1.5。A组仿真参数和数值分析中一致，B组除k1=2 200 kN/m和kψ1=1 760 kN/rad外，其他参数均与数值分析环节相同。

由图5(a)，A组仿真电机平均转速约为953 r/min，即运转速度ω=99.7 rad/s，对应于图2和图4中特性点A。B组仿真转速约为971 r/min(运转速度ω=101.6 rad/s)，同时基于仿真参数的固有频率为ωn0=87.3 rad/s。数值定性分析和仿真中的频率比相同，即ωm0/ωn=ω/ωn0。求得ωm0≈205.6 rad/s，对应于图2和图4中点B。

由于选用两相同电机，系统很快达到同步运行状态，A和B两组仿真的稳定相位差分别为0°和180°，该结果与图2中A和B两点数值结果对应一致。在15 s时，对激振器2施加大小为π/3的干扰，随后转速和相位差曲线均短暂波动，但都迅速恢复至干扰前的稳定状态，说明系统稳定性较强。

从运动位移角度，当相位差为0时，两个激振器产生的激振力叠加，两质体间实现相对圆周运动。与质体1(内圆柱体)振幅相比，质体2(隔振质体)的振幅非常小，即系统隔振效果较好，见图5(f)。A组仿真中，两个质体在x和y方向的相对运动振幅均接近1.9 mm。对B组仿真，由于相位差为180°，激振力相互抵消，两个质体的运动位移约为0，机体几乎静止，见图5(d)和图5(f)。同时，两组仿真内外质体的摆角均接近0，说明在振动过程中机体基本无摆动。相对运动振幅仿真结果与图4中A和B两点的数值结果基本一致。

根据以上定量对比，仿真结果与数值分析结果对应相同，检验了理论方法的有效性。

在工程中，参考图1(a)所示动力学模型设计振动球磨设备时，可选择交流电机作为激振器动力源，电机通过联轴器带动偏心转子高速回转产生激振力。主振质体m1一般采用具有一定厚度的磨筒，待磨物料(例如高级化学物质)和磨介(钢球、钢棒和陶瓷球等)置于磨筒内的空腔中。设备功能的实现建立在激振器同步运行和系统工作点合理选择的基础上。根据数值分析和仿真结果，当系统参数选定在图2中区域I，且设备工作在亚共振或亚近共振区域时，两激振器以0相位差同步稳定运行，主振质体(磨筒)的运动形式为高频大振幅圆周运动，见图5(f)。此时，磨筒内的物料和磨介近似均匀地紧贴在筒壁上并实现高速圆周摩擦运动，引起磨介对物料的强烈冲击、挤压和摩擦，达到物料断裂、粉碎、研磨和细化等加工目的。

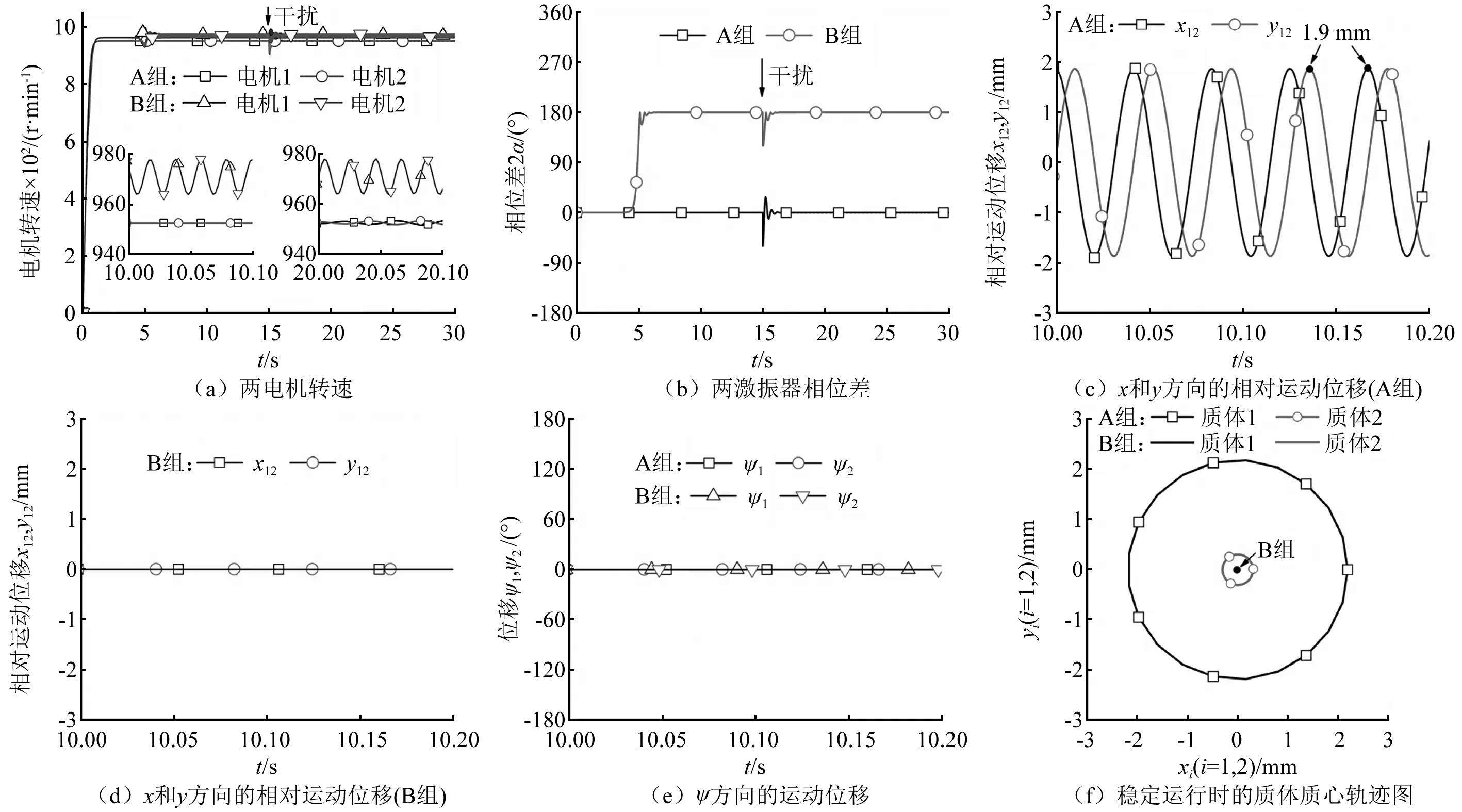
图5 系统仿真结果Fig.5 Simulation results of the system

5 结 论

(1) 利用平均法和Hamilton原理分别推导出系统同步性和稳定性理论判据。同步性判据要求两电机有效电磁输出转矩之差的绝对值应小于或等于系统频率俘获力矩。稳定性判据要求稳定能力系数与两激振器相位差余弦值的乘积大于0。

(2) 通过数值方法讨论了系统同步稳定区域和相对运动幅频特性。同步稳定区域决定系统最终运动类型，主要取决于两个因素：无量纲参数rl和操作频率ωm0。前者与系统结构参数有关，后者依赖于外部电源频率。

(3) 对应本文动力学模型的振动机械，应在区域Ⅰ内选择无量纲参数rl的值，同时操作频率ωm0需设定在ωn的亚共振区或亚近共振区。此时，两激振器产生的激振力正向叠加，两质体间主要运动形式为相对圆周运动。