振动压路机作业引起地基振动的解析法研究

王立安， 余云燕

(兰州交通大学 土木工程学院，兰州 730070)

交通基础设施的大规模建设，在促进经济发展的同时也带来了诸多负面影响，例如噪音污染、环境振动等问题。交通网的密集布置使越来越多的民房和古建筑处于道路沿线，交通荷载引起的环境振动问题愈加受到社会关注。为此，近些年学者们[1-6]关于轨道和汽车交通引起的地基振动问题做了大量研究，并取得显著成果。然而，在道路建设中，使用振动压路机对地基进行压实从而提高地基承载力，是目前道路施工中采用的主要途径。相较于交通荷载产生的地基振动，振动压路机作业产生的振幅更大、频率特征更复杂[7-8]，由此造成的环境振动危害更甚。有鉴于此，深入研究振动压路机作业引起的地基振动，对环境振动影响预测和控制有着重要意义，也对振动压路机的作业参数设计起到指导作用。

回顾过去对振动压路机引起地基振动的研究，大多通过现场测试的方法进行，如：卢辉等[9]通过采集振动压路机作业产生的地表振动信号，研究了隔振沟的隔振效果；张志峰等[10]采用相同的现场测试方法，研究了振动压路机诱发地表振动的衰减规律和频率特征。然而，通过现场测试只能获得地表的振动信号，对于地层深处的振动信号则很难采集，无法分析振动沿深度的传播规律，而且测试结果中掺杂了环境背景振动，影响分析结果的可靠性。也有学者采用数值模拟的方法对该问题做了研究，如：苏卫国等[11]在ANSYS有限元软件中通过输入振动压路机的激振力，分析了地基中埋置光缆的振动响应。该数值模型未反映压路机激振力的动态移动，也未反映压路机的激振频率及振幅，仿真程度非常有限；Kenneally等[12]采用时变接触单元和动态有限元算法对振动压路机与地基的动力相互作用做了较好的模拟，并与实测结果做了对比验证。截止目前，采用解析法研究该问题的文献还非常少。Beainy等[13]采用解析法对振动压路机钢轮和地基的运动方程进行耦合求解，分析了地基的振动响应。沈培辉等[14]建立7自由度振动压路机与Winkler地基的耦合动力控制方程，并进行解析求解，针对压路机系统的振动响应做了研究。上述两种解析模型都只考虑了振动压路机激振力在时域上的间隔作用，而没反映激振力在空间上的移动，相当于压路机在原地进行激振作业，与压路机的实际工作状态不符。Cai等[15-16]对移动荷载作用下地基的振动响应做了系统研究。Lu等[17]对移动简谐荷载作用下的地基振动响应做了解析研究。然而，振动压路机的激振力并非移动简谐荷载，而是移动的间隔冲击荷载，所以，该研究模型也不适用于振动压路机。

综上分析，对振动压路机引起的地基振动进行解析计算时，不仅要考虑压路机激振力在时间上的间隔，还需考虑压路机移动造成的空间上的间隔。因此，本文利用Shah函数和Heaviside阶跃函数将压路机的激振作用描述为关于时间和空间坐标的解析函数，并将其代入弹性半空间的动力控制方程进行联立求解。利用三重Fourier变换推导出频率-波数域的解析解，然后反演到时间-空间域。通过数值算例，研究了振动压路机引起地基振动的衰减规律和频谱特征，并对压路机激振频率、名义振幅和行驶速度的影响做了分析。

1 问题模型

振动压路机钢轮与地基动力作用的力学模型，如图1所示。图1中：M0为钢轮质量；m0，ω0和e0分别为钢轮内偏心转子的质量、转动角速度及偏心距；Fd为偏心转子转动产生的激振力；A0为钢轮的名义振幅；c为压路机行驶速度； 2a，2b为钢轮在地表作用印迹的长和宽；qd(x,y,t)为任意t时刻作用于地表的冲击力集度；本文着重研究振动压路机对地基的振动输入，故而将地基考虑为较简单的均质弹性半空间。建立空间三维直角坐标系x-y-z，各坐标轴选取见图1。

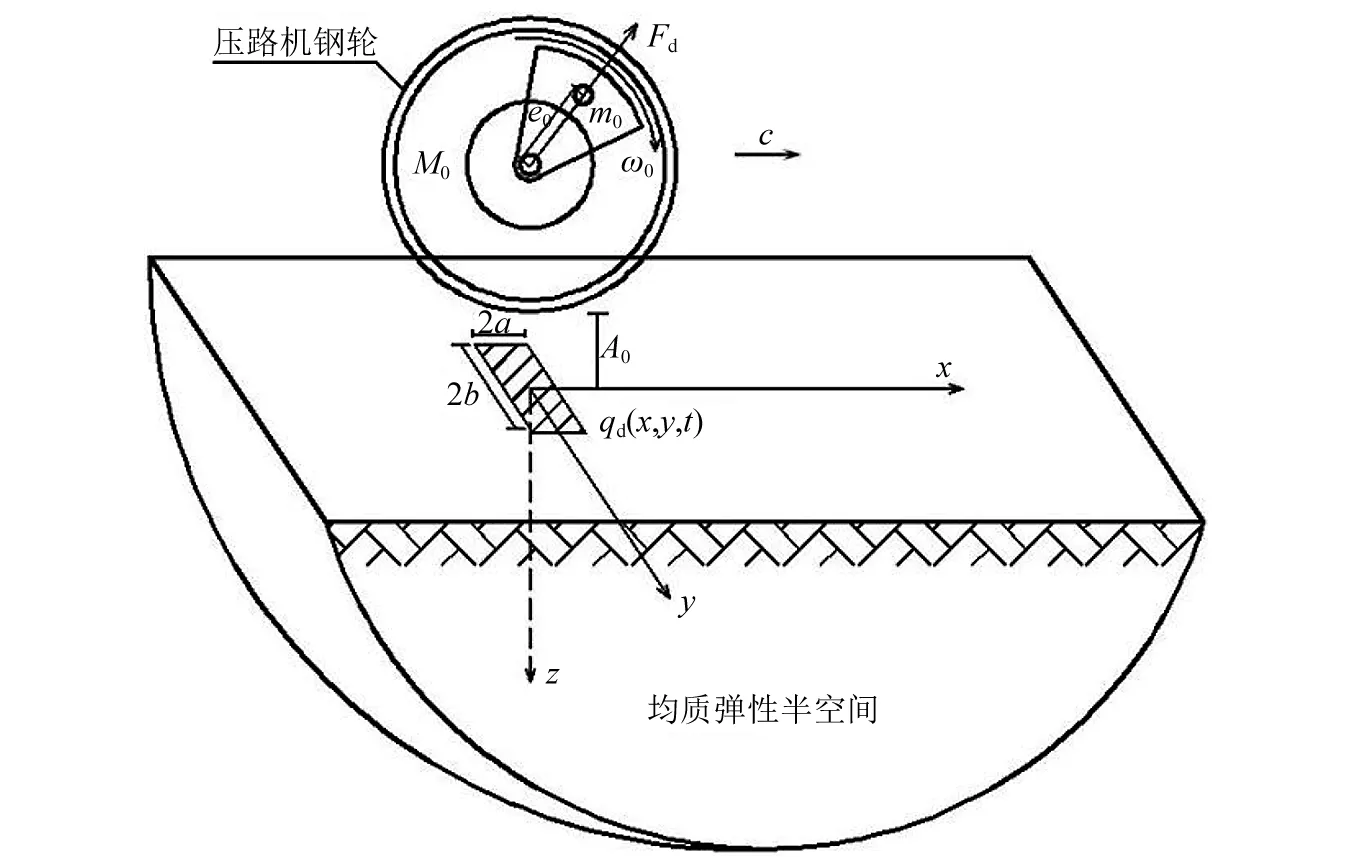
图1 计算模型Fig.1 Calculation model

由钢轮运动方程，可得到偏心转子产生的激振力Fd[18]

(1)

钢轮对地表激振的频率和周期为

(2)

2 压路机动力作用的数学描述

振动压路机钢轮作用于地表的冲击力qd(x,y,t)，在时域上为以周期T为间隔的一系列冲激序列，如图2(a)所示，在空间上为沿行驶方向(x轴)以cT为间隔的冲激序列，如图2(b)所示。则利用符号函数并结合式(1)和式(2)，将qd(x,y,t)写为

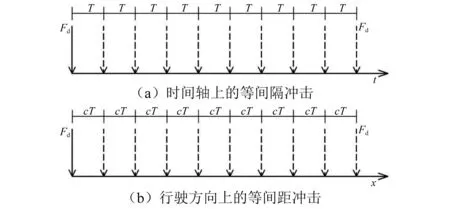
图2 时间和空间上的间隔冲击作用Fig.2 Roller excitation load in time and space domain

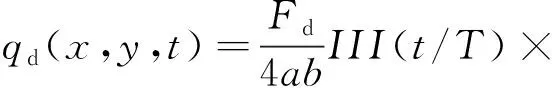
(3)

式中：III()为Shah冲激序列函数(又称梳状函数)；H()为Heaviside阶跃函数。其定义分别为

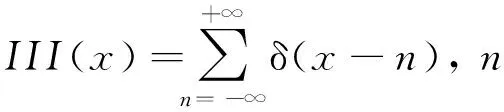
(4)

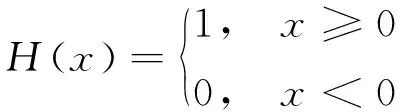
(5)

式中，δ()为Dirac-delta函数，定义为

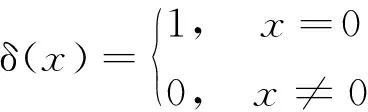
(6)

3 地基动力方程求解

空间直角坐标系下，均质弹性半空间的运动方程为

(7)

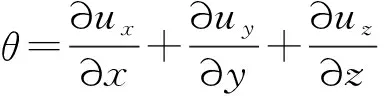
本构方程

(8)

式中，σxz，σyz，σz为地基中一点的应力分量。对时间坐标t引入如下Fourier变换对

(9)

式中： “～”为对应物理量的Fourier变换；s为变换参数。

利用式(9)对式(7)进行Fourier变换后，得到

(10a)

(10b)

(10c)

(11)

再对x，y坐标引入双重Fourier变换

(12)

式中，ξ，η为对应于x，y坐标的Fourier变换参数。

(13)

求解式(13)，得到

(14)

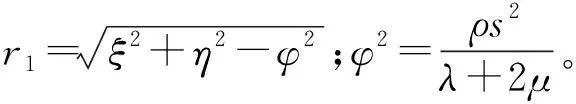
对式(10)也进行双重Fourier变换，并将式(14)代入，整理后得到

(15)

(16)

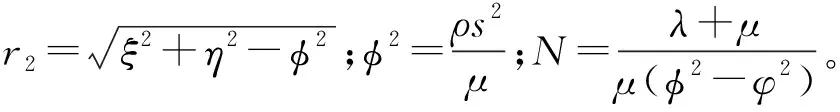
对本构式(8)做时间和空间坐标的三重Fourier变换，并将式(14)、式(16)代入，得出变换域中地基的应力通解

(17)

4 边界问题求解

不考虑钢轮与地基之间的切向摩擦，则半空间表面(z=0)处的边界条件写为

(18)

对式(18)做三重Fourier变换后得到

(19)

对式(3)也进行三重Fourier变换，得到

(20)

(21)

式中，“*”为卷积运算。利用Shah函数的卷积性质[19]，式(21)进一步写为

(22)

将式(20)、式(16)及式(17)代入式(19)，并取z=0，则得到关于A1～A3的线性方程组

(23)

求解式(23)，则得出A1～A3

(24)

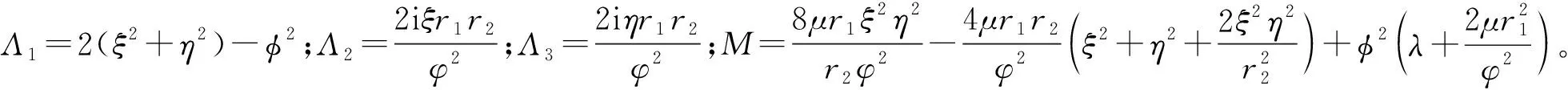
将式(24)回代到式(16)，则得到地基位移在变换域中的解

(25)

通过对式(25)做三重Fourier逆变换，则可反演出时间-空间域中位移的解析解，进而可得出应力解。

5 验证与分析

对前文推导结果进行编程计算，关于式(25)的Fourier逆变换可通过数值积分或离散Fourier逆变换(inverse discrete Fourier transform，IDFT)实现，本文中采用计算效率较高的IDFT法进行反演。为使计算结果能以振源为中心沿中心分布，引入移动坐标轴Xt，Xt=x-ct。

5.1 算法验证

若将本文计算模型中振动压路机的行驶速度c取为0，则退化为地基表面定点作用周期冲击荷载的问题，退化模型与文献[20]相同。为进行对比验证，计算参数按Mandikizinoyou等的研究选取。通过取M0=500 kg，A0=0.5 mm，f=10 Hz，2a=2b=1 m使Fd/4ab=1 kPa(与Mandikizinoyou等的研究相同)。地基参数取值为：E=3.5 MPa，v=0.3，ρ=1 800 kg/m3。图3给出了t=0.1 s和t=0.5 s时刻，地表沿x轴分布的竖向振动位移退化解与Mandikizinoyou等的研究结果对比，如图3所示。由图3可知，两者能够很好地吻合，从而验证了本文算法和计算程序的可靠。

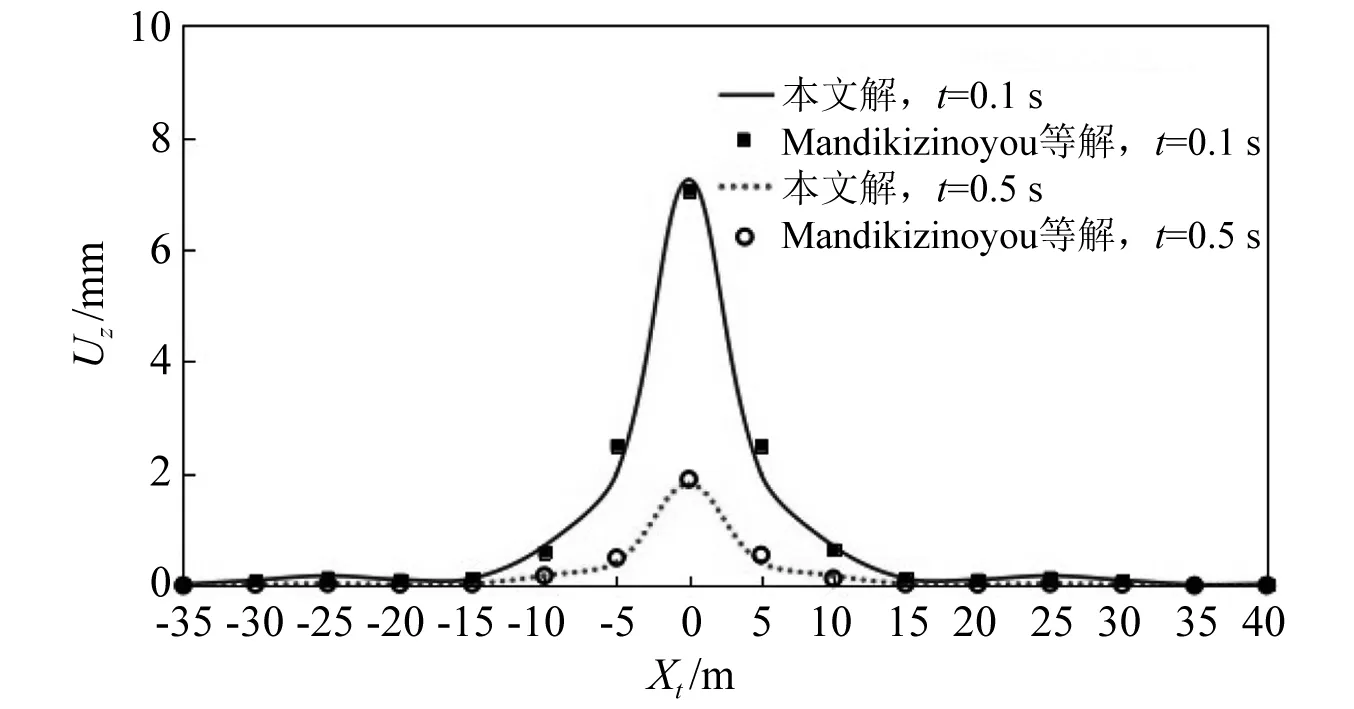
图3 退化计算及结果对比Fig.3 Degradation calculation and comparison

5.2 振动衰减分析

参照SSR220AC型振动压路机的相关技术参数给出本文模型所需的计算参数，如表1所示。地基参数取值与5.1节相同。

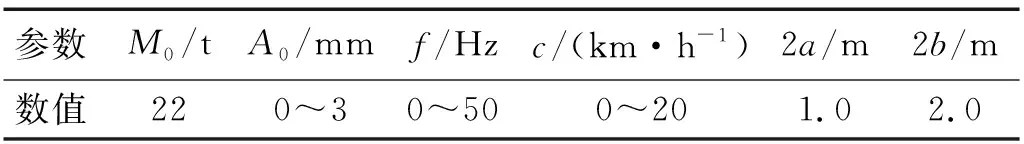
表1 压路机技术参数Tab.1 Parameters of vibratory roller operation

图4为计算出的t=0.1 s时刻，地表竖向位移的空间分布。对比图4(a)～图4(c)发现，压路机激振频率f对地表振幅的影响非常小，而名义振幅A0对地表振幅影响显著。从图4(b)还能发现，地表振动位移沿纵向(x轴方向，压路机行驶方向)和横向(y轴方向)的分布存在差异。图5中的轴线分布图进一步表明，地表振动位移沿纵、横向分布明显不同，在近场区域(≤20 m)，纵横向分布差异较大，近场区域振幅沿横向衰减更快，而在远场几乎趋于一致；压路机名义振幅A0越大，近场区域纵、横向分布差异越大。

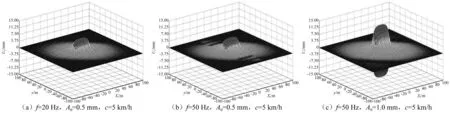
图4 地表竖向位移分布Fig.4 Distribution of vertical displacement on the surface

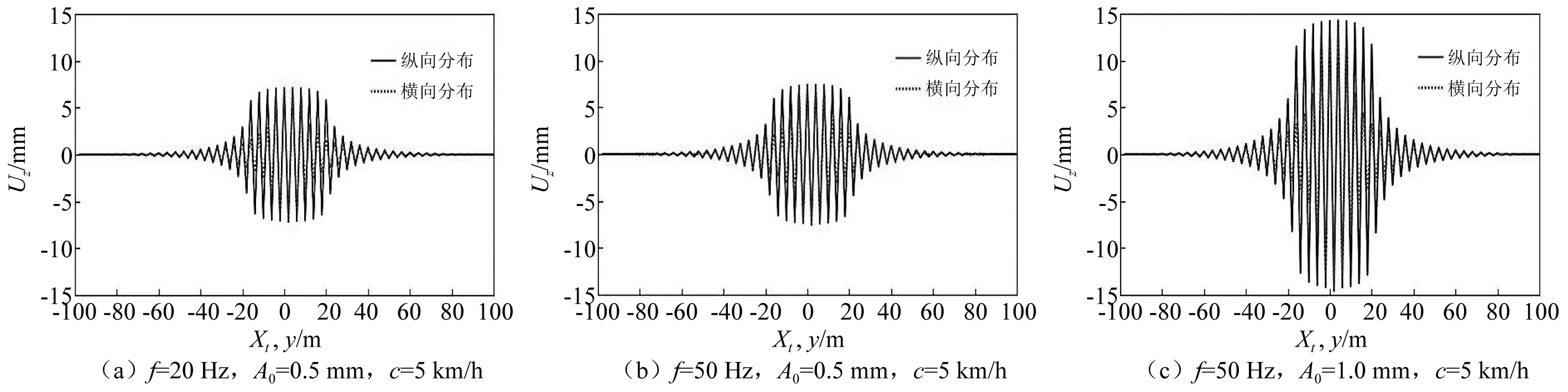
图5 地表竖向位移轴线分布Fig.5 Distribution of vertical displacement on surface along axis

图6在0～20 km/h区间内考察了地表振动位移随压路机行驶速度的变化(压路机行驶速度通常不超过15 km/h)。分析图6发现，随着压路机行驶速度增大，地表振幅先增大后减小，在大约5 km/h附近出现拐点，压路机激振频率越大，拐点数越多。出现这一现象的原因可推测为：当压路机行驶速度较低时，地基对于钢轮的前次激振和后次激振产生的响应为正向叠加；当行驶速度加快时，则逐渐演变为反向叠加。钢轮激振频率增大时，使正、反向叠加交替出现，从而出现拐点数增多的现象。图6(b)进一步显示，压路机名义振幅越大，地表振幅越大。

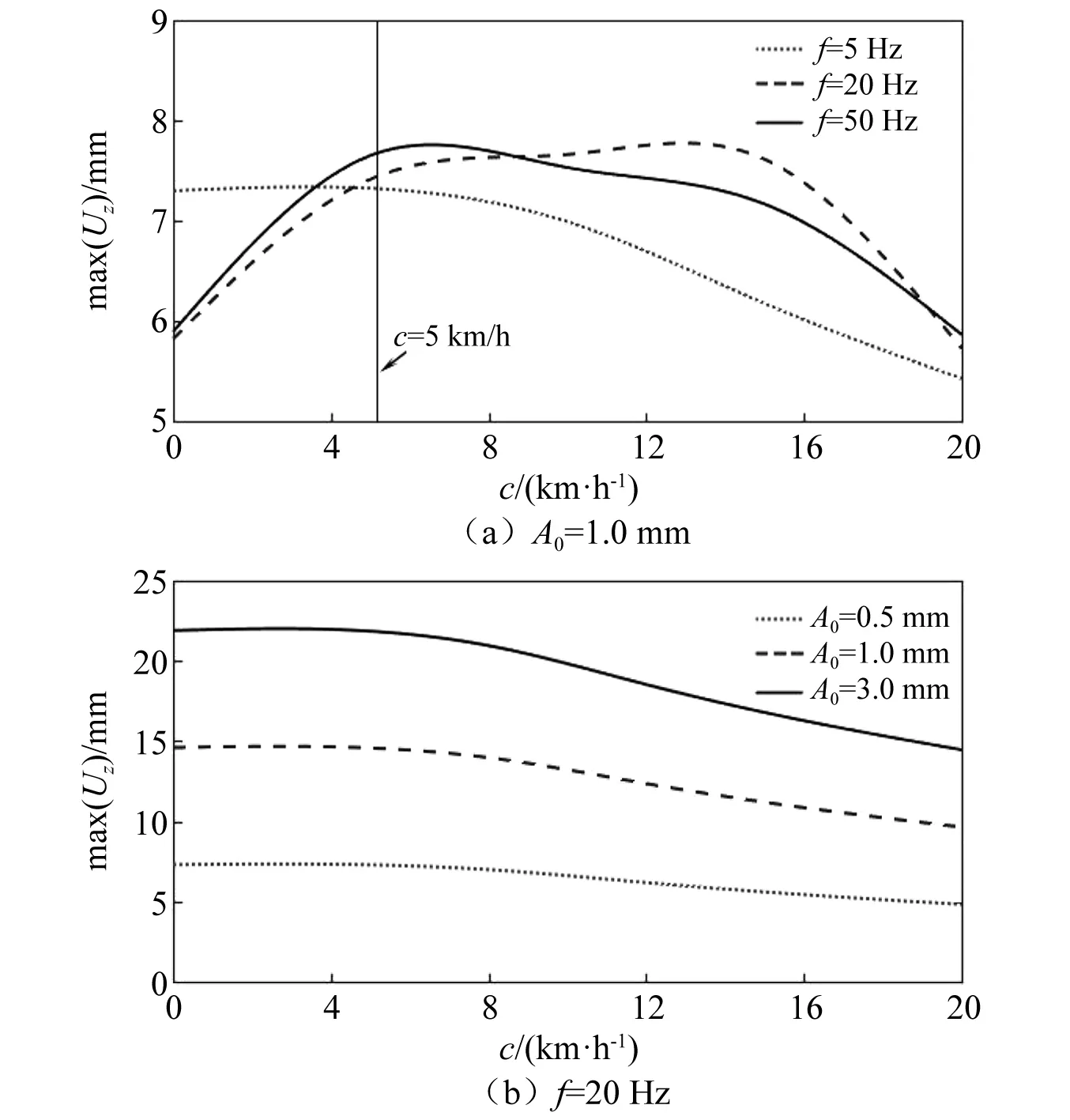
图6 地表振幅随压路机行驶速度的变化Fig.6 Variation of surface amplitude with roller speed

地基振幅沿深度的衰减曲线，如图7所示。从图7中能够分析出，压路机激振频率对振幅沿深度的衰减几乎无影响，压路机名义振幅由于改变了地表振幅，从而也影响了振幅沿深度的衰减。对于本文中的均质弹性地基而言，压路机振动影响深度约为名义振幅的800倍。

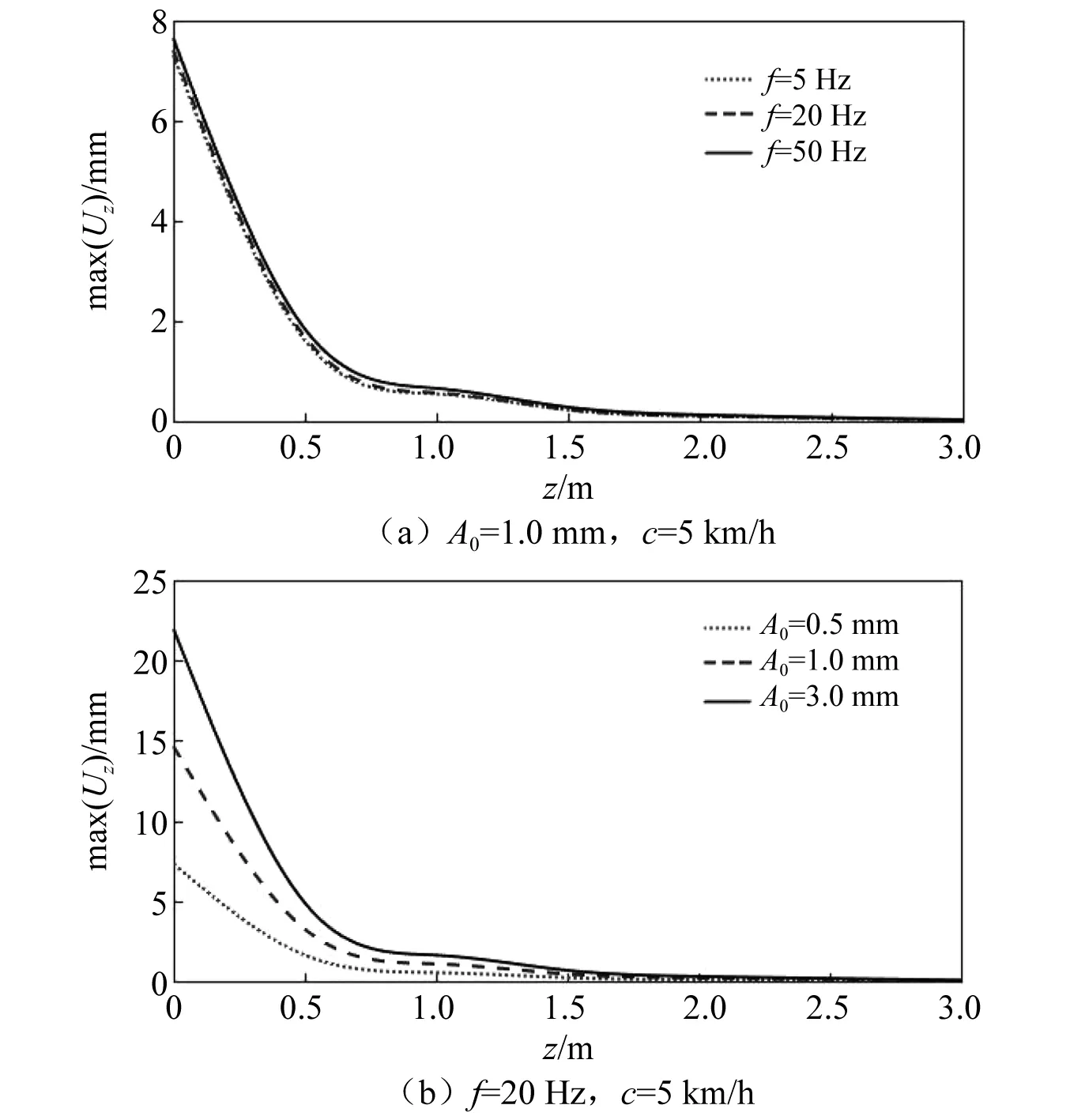
图7 振幅沿深度的衰减Fig.7 Attenuation of ground amplitude along depth

5.3 频谱分析

在地表确定一个观测点D1(5 m, 3 m)，计算出该点连续时刻的位移值，即可得到该测点的位移时程曲线，如图8(a)所示。对位移时程曲线关于时间t求一阶导，则得到振动速度的时程曲线，如图8(b)所示，对时程曲线做Fourier变换则进一步得到频谱曲线，如图9所示。分析图9发现，压路机激振频率对地表振动的频率分布影响较大，激振频率越大，峰值频率的数目越多，峰值频率分布的频带越宽。图9(b)显示，名义振幅只改变了地表振幅，而对频率分布没有影响。

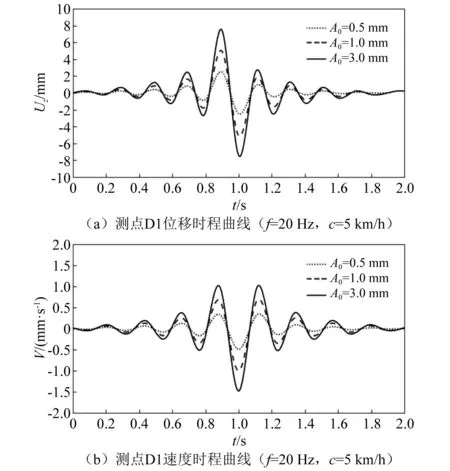
图8 测点D1的位移和速度时程曲线Fig.8 Time history curve of displacement and velocity at D1

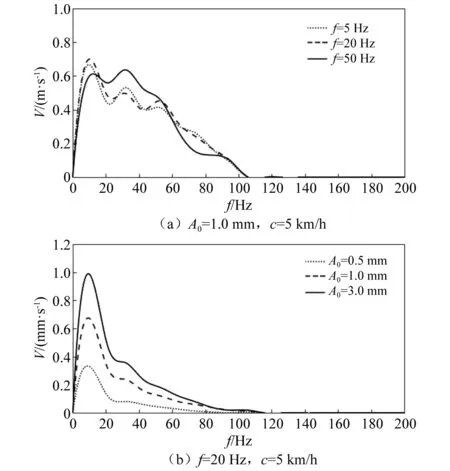
图9 测点D1的频谱曲线Fig.9 Spectrum curve at D1

6 结 论

利用Shah函数和Heaviside阶跃函数描述振动压路机的激振作用，并推导出地基振动位移解析解。通过算例分析，总结出以下结论：

(1) 振动压路机引起的地表振幅沿纵、横向的衰减存在较大差异，在近场区域(≤20 m)横向衰减更快，在远场则趋于一致。

(2) 压路机激振频率对地基振幅影响甚微，而对频率分布影响较大，激振频率越大，峰值频率的数目越多，峰值频率分布的频带越宽。压路机名义振幅对地基振幅的影响显著，但对振动频率无影响。

(3) 地基振幅随压路机行驶速度的变化没有单调性，出现先增大后减小的现象，在大约5 km/h附近出现拐点。当压路机激振频率增大，拐点数将增多。